Контрольная работа__Векторы в пространстве. Контрольная работа _Векторы в пространстве. Контрольная работа по теме Векторы в пространстве

• Название: Контрольная работа по теме Векторы в пространстве
• Анкор: Контрольная работа__Векторы в пространстве
• Дата: 30.04.2022
• Размер: 24.88 Kb.
• Имя файла: Контрольная работа _Векторы в пространстве.docx
• Тип: Контрольная работа; #506156

Контрольная работа по теме: «Векторы в пространстве»
I вариант

1 часть

Изобразите параллелепипед ABCDA₁B₁C₁D₁.

1. 
   Найдите вектор, равный сумме векторов АВ, А₁D₁ и СА₁.
   
2. 
   Найдите вектор, равный .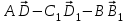
   
3. 
   Представьте вектор ВС₁ в виде разности двух векторов, один из которых вектор ВD₁.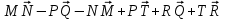
   
4. 
   Упростите выражение: .
   
5. 
   Упростите выражение: .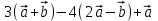
   

2 часть

6. 
   Дан прямоугольный параллелепипед KLMNK1L1M1N1. Докажите, что: |MK + MM1| = |MK - MM1|.
   
7. 
   Точки Е и F — середины оснований АВ и ВС параллелограмма ABCD, а О — произвольная точка пространства. Выразите вектор ОА — ОС через вектор EF.
   

3 часть

8. Три точки М, N и Р лежат на одной прямой, а точка О не лежит на этой прямой. Выразите вектор ОР через векторы ОМ и ON, если NP = 2MN.
II вариант

1 часть

Изобразите параллелепипед ABCDA₁B₁C₁D₁.

1. 
   Найдите вектор, равный сумме векторов СА₁, АD и D₁C₁.
   
2. 
   Найдите вектор, равный .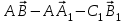
   
3. 
   Представьте вектор ВС₁ в виде разности двух векторов, один из которых вектор D₁B.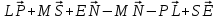
   
4. 
   Упростите выражение: .
   
5. 
   Упростите выражение: .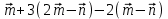
   

2 часть

6. 
   Дан прямоугольный параллелепипед KLMNK1L1M1N1. Докажите, что: |NL - M1L| = |K1N - LN|.
   
7. 
   Точки Е и F — середины оснований АВ и ВС параллелограмма ABCD, а О — произвольная точка пространства. Выразите вектор ОА — ОЕ через вектор DC.
   

3 часть

8. Три точки М, N и Р лежат на одной прямой, а точка О не лежит на этой прямой. Выразите вектор ОР через векторы ОМ и ON, если МР = -½PN.