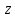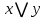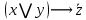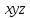Контрольная работа. Раздел Множества
 Скачать 267.44 Kb. Скачать 267.44 Kb.
|
1 2 4. Раздел «Булевы функции» Для данной формулы булевой функции: а) найти ДНФ, КНФ, СДНФ, СКНФ методом равносильных преобразований; б) найти СДНФ, СКНФ табличным способом (сравнить с СДНФ, СКНФ, полученными в пункте “а”); в) указать минимальную ДНФ и соответствующую ей переключательную схему. 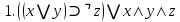 Для удобства знак конъюнкции (логического умножения) будем опускать, знак отрицания будем обозначать чертой над переменной, а знак импликации – стрелкой. Заданная функция:  а) Заменяем импликацию по правилу  : : Используем закон де Моргана: 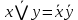 ; в итоге получаем ДНФ -дизъюнктивную нормальную форму: ; в итоге получаем ДНФ -дизъюнктивную нормальную форму: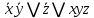 Из неё можно получить СДНФ – совершенную дизъюнктивную нормальную форму. Будем использовать закон единицы, закон исключённого третьего, закон дистрибутивности:  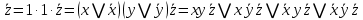 Теперь, учитывая каждую конъюнкцию только 1 раз, получаем СДНФ:  Чтобы получить КНФ, воспользуемся полученной ДНФ: 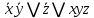 . Используем закон . Используем закон 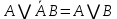 , тогда (здесь используем также закон снятия двойного отрицания): , тогда (здесь используем также закон снятия двойного отрицания): 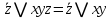 . Тогда упрощённая ДНФ: . Тогда упрощённая ДНФ: Используя закон дистрибутивности, закон противоречия и закон нуля, получаем:  Получаем: 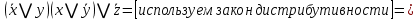 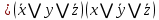 Получили конъюнктивную нормальную форму – КНФ: 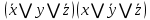 Эта же форма является СКНФ, т.к. в каждой дизъюнкции участвуют все переменные. б) Найдём теперь СДНФ, СКНФ табличным способом. Составляем последовательно таблицу истинности для заданной функции  . Учитываем, что отрицание меняет истинность, дизъюнкция ( . Учитываем, что отрицание меняет истинность, дизъюнкция (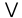 ) ложна только в том случае, когда оба операнда ложны, конъюнкция истинна только в том случае, когда оба операнда истинны, импликация ( ) ложна только в том случае, когда оба операнда ложны, конъюнкция истинна только в том случае, когда оба операнда истинны, импликация (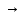 ) ложна только в том случае, когда из истины следует ложь. ) ложна только в том случае, когда из истины следует ложь.
Используя наборы, на которых функция принимает значение 1, составляем совершенную дизъюнктивную нормальную форму - СДНФ: в каждую конъюнкцию переменная входит с отрицанием, если в соответствующем наборе она имеет значение 0 (знак конъюнкции – логического умножения опускаем для удобства): 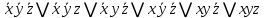 Получили такую же форму СДНФ, как и раньше, только с перестановкой членов (но форма одна и та же). Используя наборы, на которых функция принимает значение 0, составляем совершенную конъюнктивную нормальную форму - СКНФ: в каждую дизъюнкцию переменная входит с отрицанием, если в соответствующем наборе она имеет значение 1:  Получили такую же форму СКНФ, как и раньше, только с перестановкой членов (форма одна и та же). в) Ранее была получена ДНФ: 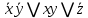 . Она является минимальной, уменьшить в ней число переменных уже нельзя. Построим по этой форме переключательную схему. В этой форме – три конъюнкции, значит схема будет состоять из трёх параллельных ветвей. Каждая конъюнкция реализуется последовательным соединением элементов в ней. Получаем: . Она является минимальной, уменьшить в ней число переменных уже нельзя. Построим по этой форме переключательную схему. В этой форме – три конъюнкции, значит схема будет состоять из трёх параллельных ветвей. Каждая конъюнкция реализуется последовательным соединением элементов в ней. Получаем:   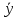 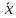   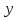 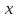   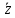 1 2 |