Документ Microsoft Word (2). И составное высказывание. Такое высказывание называют конъюнкцией (от латинского слова единение). Обозначают (читают а и

• Название: И составное высказывание. Такое высказывание называют конъюнкцией (от латинского слова единение). Обозначают (читают а и
• Дата: 12.03.2023
• Размер: 2.04 Mb.
• Имя файла: Документ Microsoft Word (2).docx
• Тип: Документы; #982731
• страница: 1 из 3

 Введение в анализ.

1. Истинные и ложные высказывания, истинность высказываний А И В, А ИЛИ В. Отрицание конъюнкции и дизъюнкции.

Пусть А и В – произвольные высказывания. Образуем из них с помощью союза «и» составное высказывание. Такое высказывание называют конъюнкцией (от латинского слова «единение»).

Обозначают (читают:А и В).1 

 

Конъюнкцией n высказываний называется предложение вида , которое истинно тогда и только тогда, когда истинны все составляющие его высказывания. (Логическое умножение)

Дизъюнкцией n высказываний называется предложение вида , которое ложно тогда и только тогда, когда ложны все состав­ляющие его высказывания. (Логическое сложение)

 

2. Кванторы. Отрицание высказывания Ɐ Р(x) и ∃ Р(х).

Высказывания с кванторами

Рассмотрим примеры.

1. Пусть на множестве N задана высказывательная форма А(х): «Число х кратно 3». Поставим перед высказывательной формой слово «всякое». Получим ложное высказывание: «Всякое число х кратно 3» (х ÎN). Поставив перед данной высказывательной формой слово «существует», получим истинное высказывание: «Существует число х, кратное 3» (х Î N).

2. Рассмотрим числа: 1, 2, 3, 4, 5. Про них можно сказать: «Все числа однозначные. Некоторые из данных чисел чётные».

Относительно этих предложений имеет смысл вопрос, истинны они или ложны, следовательно эти предложения – высказывания.

Итак, высказывательную форму (предикат) можно превратить в высказывание, поставив перед формой особые слова, которые называются логике кванторами.

Слово «квантор» произошло от латинского «quantum», что означает «сколько».

Квантором называют символ математической логики, указывающий на определенную логическую операцию, которую необходимо осуществить, чтобы дать количественную характеристику некоторой области объектов.

Таким образом, квантор показывает, о скольких объектах (элементах) говорится в том или ином высказывании.

Различают два основных вида кванторов: квантор общности и квантор существования. Под квантором общности понимаются слова: «любой», «каждый», «всякий», «все», а под квантором существования подразумеваются слова и обороты: «существует», «найдется хотя бы один», «есть», «имеется».

Пусть Р(х) – высказывательная форма (предикат), заданная на множестве Х. Поставив перед ней квантор общности, получим высказывание: «Для всех хÎХ выполняется высказывательная форма Р(х)», которое записывается в символах: (xÎX) P(x).

Символ – это перевернутая первая буква английского слова «All» - «все».

Высказывание, содержащее квантор общности, истинно в том и только в том случае, если для всех элементов х из множества Х выполняется высказывательная форма Р(х); если же хотя бы для одного элемента х из множества Х высказывательная форма Р(х) не выполняется, то высказывание с квантором общности будет ложно.

Если перед высказывательной формой Р(х), хÎХ, поставить квантор существования, то получим высказывание: «Существует такое хÎХ, что выполняется высказывательная форма Р(х)». В символах оно записывается:

(х ÎХ) Р(х).

Символ - это перевёрнутая справо налево первая буква английского слова «Exist» – «существует».

Высказывание, содержащее квантор существования, истинно в том и только том случае, если хотя бы для одного элемента х из множества Х выполняется высказывательная форма Р(х); если же ни для одного элемента х из множества Х высказывательная форма Р(х) не выполняется, то высказывание с квантором существования ложно.

Например, пусть на множестве N натуральных чисел задана высказывательная форма Р(х): «Число х больше 5». Используя кванторы, из высказывательной формы можно получить, например, следующие высказывания: 1) «Любое натуральное число х больше 5»; 2) «Каждое натуральное число х больше 5»; 3) «Существует натуральное число х, большее 5»; 4) «Найдется натуральное число х, большее 5».

Первые два высказывания имеют одинаковый смысл, они ложны, и в символах запишутся: (xÎN)P(x). Последние два высказывания истинны и имеют запись: (xÎN) P(x).

Чтобы установить значение истинности высказываний с кванторами, надо знать некоторые правила.

Истинность высказываний с квантором общности устанавливается путем доказательства. Чтобы убедиться в ложности достаточно привести контрпример.

Истинность высказывания с квантором существования устанавливается при помощи конкретного примера. Чтобы убедиться в ложности, необходимо провести доказательство

 

3. Отображение. Равенство двух отображений. Инъекция, сюръекция, биекция.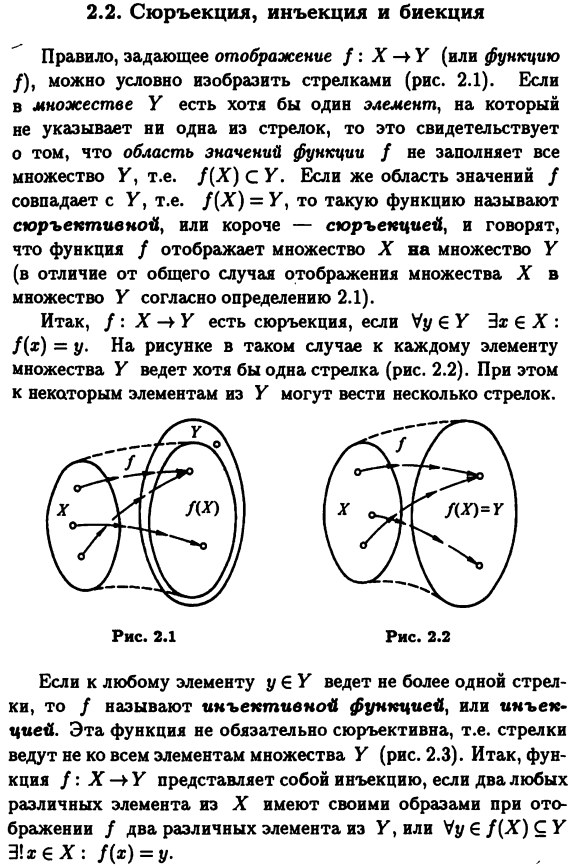

1)Функция  – отображает множество действительных чисел на множество действительных положительных чисел. Это отображение – сюръекция, т.к. разным x соответствуют одинаковые y;

2) Функция  – отображает множество положительных действительных чисел на множество действительных положительных чисел. Это отображение – инъекция, но не сюръекция, т.к.  для любых  ;

3) Функция y = 4x+7 – отображает всю числовой ось  на себя. Это отображение – биекция.

 

4. Композиция отображений. Примеры коммутирующих и некоммутирующих отображений.



5. Обратное отображение

Вкратце: если отображение биективное, то для него существует обратное отображение



1. Множества и мощности

1.1. Множества

Основные понятия и обозначения, связанные с множествами и операциями над ними:

•Множества состоят из элементов. Запись x M означает, что x является элементом множества M.

•Говорят, что множество A является подмножеством множества B (запись: A B), если все элементы A являются элементами B.

•Множества A и B равны (запись: A = B), если они содержат одни и те же элементы (другими словами, если A B и B A).

•Если A — подмножество B, не равное всему B, то A называют собственным подмножеством B (запись: A ( B).

•Пустое множество не содержит ни одного элемента и является подмножеством любого множества.

•Пересечение A ∩B двух множеств A и B состоит из элементов, которые принадлежат обоим множествам A и B. Это записывают так:

A ∩ B = {x | x A и x B}

(читается: множество таких x, что . . . ).

•Объединение A B состоит из элементов, которые принадлежат хотя бы одному из множеств A и B:

A B = {x | x A или x B}.

•Разность A\B состоит из элементов, которые принадлежат A, но не принадлежат B:

A \ B = {x | x A и x / B}.

Если множество B является подмножеством множества A, разность A \ B называют также дополнением B до A.

 

6. Равномощные множества. Равномощность N и Z. Равномощность отрезка и интеревала.

. Равномощные множества

Два множества называют равномощными, если между ними можно установить взаимно однозначное соответствие, при котором каждому элементу одного множества соответствует ровно один элемент другого.

Для конечных множеств это означает, что в них одинаковое число элементов, но определение имеет смысл и для бесконечных множеств. Например, отрезки [0, 1] и [0, 2] равномощны, поскольку отображение x 7→2x осуществляет искомое соответствие.

Множество называется счётным, если оно равномощно множеству N натуральных чисел, то есть если его можно представить в виде {x0, x1, x2, . . . } (здесь xi — элемент, соответствующий числу i; соответствие взаимно однозначно, так что все xi различны).

Например, множество целых чисел Z счётно, так как целые числа можно расположить в последовательность 0, 1, −1, 2, −2, 3, −3, . . .

Теорема 2. (а) Подмножество счётного множества конечно или счётно.

(б) Всякое бесконечное множество содержит счётное подмножество.

(в) Объединение конечного или счётного числа конечных или счётных множеств конечно или счётно.

Есть отрезок [a, b] и интервал (a, b). Построим биекцию [a, b] -> (a, b). Для этого разобъём обоих на три части и построим три отдельных биекции. 1) [a, c) -> (a, c): a -> середина, т. е. (a+c)/2 (a+c)/2 ->середина правой половины, т. е. (a+3c)/4 (a+3c/4) -> середина правой четверти, т. е. (a+7c)/8 и т. д. все остальные точки отобразить на самих себя. 2) c -> c 3) (c, b] -> (c, b): b -> середина, т. е. (c+b)/2 (c+b)/2 ->середина левой половины, т. е. (3c+b)/4 и т. д. остальные точки отобразить на самих себя.

т. е. достаточно было доказать равномощность отрезка и полуинтервала

 

7. Счетные множества. Счетность Z и Q, счетность множества точек на плоскости с целыми координатами.

 Множество, эквивалентное множеству натуральных чисел N = {1, 2, 3, …, n,…}, называется счетным.

Можно сказать также, что множество счетно, если его элементы можно перенумеровать.

Теорема 1. Всякое бесконечное подмножество счетного множества счетно.

Пример 1.21.

Множество A = {3, 6, …, 3n,…} счетно, т.к. A – бесконечное подмножество множества натуральных чисел, A Ì N.

Теорема 2. Объединение конечной или счетной совокупности счетных множеств счетно.

Пример 1.22.

Множество A = {0, 1, …, n,…} неотрицательных целых чисел счетно, множество B = {0, –1, …, –n,…} неположительных целых чисел тоже счетно, поэтому множество всех целых чисел С = АÈB = {…, –n, …– 2, –1, 0, 1, 2, …, n, …} тоже счетно.

Теорема 3. Множество всех рациональных чисел, т.е. чисел вида , гдеp и q целые числа, счетно.

Теорема 4. Если А = {a₁, a₂, …} и B = {b₁, b₂, …} – счетные множества, то множество всех пар С = {(a_k, b_n), k = 1, 2,…; n = 1, 2, …} счетно.

Пример 1.23.

Геометрический смысл пары (a_k, b_n) – точка на плоскости с рациональными координатами (a_k, b_n). Поэтому можно утверждать, что множество всех точек плоскости с рациональными координатами счетно.

Теорема 5. Множество всех многочленов P(x) = a₀ + a₁x + a₂x² + … + a_nxⁿ любых степеней с рациональными коэффициентами a₀, a₁, a₂, … a_n счетно.

Теорема 6. Множество всех корней многочленов любых степеней с рациональными коэффициентами счетно.

ОСТАЛЬНОЕ НЕ НАШЛА!

 

8. Существования несчетностного множества - канторов диагональный процесс. Определение континуума

Множество всех подмножеств натурального ряда имеет мощность большую, чем 0, и, значит, не является счетным. Мы воспроизведем доказательство (с небольшими модификациями) для этого случая, чтобы подчеркнуть лежащую в основе доказательства важную идею диагонализации.

Сопоставим каждому множеству A N его характеристическую последовательность из нулей и единиц

α0, α1, α2, …

так, что αi=1, если i A, и αi=0, если i A. Всякая последовательность из нулей и единиц является характеристической для множества, элементы которого – номера мест, содержащих единицы. Таким образом между последовательностями из нулей и единиц и подмножествами множества N устанавливается взаимно однозначное соответствие. Пусть A0, A1, A2, … – произвольный список подмножеств множества N. Покажем, что в N найдется подмножество, не попавшее в этот список. Рассмотрим список множеств A0, A1, A2, … вместе с их характеристическими последовательностями.

 

9. Теорема Кантора-Бернштейна. Равноможисоть отрезка и интервала. Равномощность круга и квадрата.

Теорема Кантора — Берштейна (в англ. литературе Теорема Кантора — Бернштейна — Шрёдера или Теорема Шрёдера — Бернштейна) утверждает, что если между двумя множествами существуют инъекции, то они равномощны.

Пусть даны два множества A и B. Тогда если существуют инъективные отображения  и  , то существует и биекция  , то есть множества A и B равномощны.

НЕ НАШЛА БОЛЬШЕ!

10. Доказательство равномощности отрезка, прямомой и плоскости через теорему Кантора-Бернштейна.

11. Почему бываю множества мощнее континнума? Теорема Кантора.

Теорема Кантора. Множество всех точек отрезка [0, 1] несчетно.

Доказательство.

Пусть множество точек отрезка [0, 1] счетно. Значит, эти точки можно перенумеровать, т. е. расположить в виде последовательности x₁, x₂ … x_n, … .

Рис. 1.7

Разобьем отрезок [0, 1] на три равные части. Где бы ни находилась точка x₁, она не может принадлежать всем отрезкам  ,  ,  . Поэтому среди них есть отрезок D₁, не содержащий точку x₁ (рис. 1.7). Возьмем этот отрезок D₁ и разделим его на три равные части. Среди них всегда есть отрезок D₂, не содержащий точку x₂. Разделим этот отрезок на три равные части и т. д. Получим последовательность отрезков D₁ É D₂ É D₃ É…ÉD_n É… . В силу аксиомы Кантора сходится к некоторой точке x при n ® ¥. По построению эта точка x принадлежит каждому отрезку D₁, D₂, D₃,…, D_n, …, т. е. она не может совпадать ни с одной из точек x₁, x₂, … x_n, …, т. е. последовательность x₁, x₂ … x_n, …не исчерпывает всех точек отрезка [0, 1], что противоречит первоначальному предположению. Теорема доказана.

Множество, эквивалентное множеству всех точек отрезка [0, 1] называется множеством мощности континуума.

Так как множества точек интервалов, отрезков и всей прямой эквивалентны между собой, то все они имеют мощность континуума.

Чтобы доказать, что данное множество имеет мощность континуума, достаточно указать взаимно однозначное соответствие между данным множеством и множеством точек отрезка, интервала или всей прямой.

Пример 1.24.

Из рис. 1.8 следует, что множество точек параболы y = x² эквивалентно множеству точек прямой –¥ < x < ¥ и, следовательно, имеет мощность континуума.

Рис.1.8

Установить мощность континуума можно также, используя следующие теоремы о множествах мощности континуума (приводятся без доказательств).

Теорема 1. Множество всех подмножеств счетного множества счетно.

Теорема 2. Множество иррациональных чисел имеет мощность континуума.

Теорема 3. Множество всех точек n-мерного пространства при любом n имеет мощность континуума.

Теорема 4. Множество всех комплексных чисел имеет мощность континуума.

Теорема 5. Множество всех непрерывных функций, определенных на отрезке [a, b] имеет мощность континуума.

Итак, мощности бесконечных множеств могут различаться. Мощность континуума больше, чем мощность счетного множества. Ответ на вопрос, существуют ли множества более высокой мощности, чем мощность континуума, дает следующая теорема (приводится без доказательства).

Теорема о множествах высшей мощности. Множество всех подмножеств данного множества имеет более высокую мощность, чем данное множество.

Из этой теоремы следует, что множеств с максимально большой мощностью не существует.

12. Определение супремума и инфинума. Аксиома полноты R. Вывод из аксомы полноты аксиомы Архимеда.

Точной (наименьшей) верхней гранью (границей), или супре́мумом (лат. supremum — самый высокий) подмножества упорядоченного множества (или класса), называется наименьший элемент, который равен или больше всех элементов множества. Другими словами, супремум — это наименьшая из всех верхних граней. Обозначается. Более формально: — множество, то есть элементов, равных или больших всех элементов.

Более формально: — множество X, то есть элементов M, равных или больших всех элементов X Точной нижней гранью, или и́нфимумом (лат. infimum — самый низкий) подмножества X упорядоченного множества M, называется наибольший элемент M, который равен или меньше всех элементов множества X. Другими словами, инфимум — это наибольшая из всех нижних граней.