Документ Microsoft Word (2). И составное высказывание. Такое высказывание называют конъюнкцией (от латинского слова единение). Обозначают (читают а и

• Название: И составное высказывание. Такое высказывание называют конъюнкцией (от латинского слова единение). Обозначают (читают а и
• Дата: 12.03.2023
• Размер: 2.04 Mb.
• Имя файла: Документ Microsoft Word (2).docx
• Тип: Документы; #982731
• страница: 3 из 3

примеры, что это действительно неопределенности не нашёл.

Определение предела функции по Коши

Число b называется пределом функции f(x) в точке a, если для ∀ϵ>0∃δ>0 такое, что для ∀x∈(a−δ;a+δ)∩D[f] из того, что0<|x−a|<δ следует, что |f(x)−b|<ϵ : limx→a f(x)=b или f(x)→b при x→a .

Определение предела функции по Гейне

Число b называется пределом функции f(x) в точке a, если для любой последовательности {xn}⊂D[f] , которая сходится к a, соответствующая последовательность значений функции {f(xn)} сходится к b.

21. Что такое предельная точка множества? Определение предела функции (по Коши). Единственность предела. лекции

​​Предельная точка множества А, такая точка x пространства, сколь угодно близко от которой имеются отличные от x точки множества А, т. е. в любой окрестности которой содержится бесконечное множество точек из А. Характеристическим свойством П. т. множества A является существование по крайней мере одной сходящейся к ней последовательности различных точек множества А. П. т. множества А не обязана ему принадлежать. Так, например, всякая точка числовой прямой является П. т. для множества А рациональных её точек: ко всякому как рациональному, так и иррациональному числу можно подобрать сходящуюся к нему последовательность различных рациональных чисел. Не всякое бесконечное множество имеет П. т. — таково, например, множество всех целых чисел. Однако всякое бесконечное и ограниченное множество любого евклидова пространства имеет по крайней мере одну П. т.

предел функции по Коши в 20 вопросе

  Докажем теорему о единственности предела последовательности. 

Теорема 1. Последовательность точек расширенной числовой прямой  может иметь на этой прямой только один предел. 

 Допустим противное. Пусть существует такая последовательность x_n  , n = 1, 2, ..., что  = a  и  = b, причем a  b, a  , b  . Возьмем какие-либо непересекающиеся окрестности U = U(а) и V = V(b) точек а и b (рис. 49): U   V = . Согласно определению предела вне окрестности U точки а, в частности в окрестности Vточки b, содержится лишь конечное число членов последовательности {x_n}. Однако точка b также является ее пределом, и потому в ее окрестности V должны находиться все члены последовательности {x_n}, начиная с некоторого номера, а следовательно, бесконечно много ее членов. Получилось противоречие. 
22. Первый замечательный предел. [Зорич, стр 136-138]

23. Определение предел функции при х - о и т.п. Определение того, что предел равен бесконечности и т.д. Виды неопределенностей и примеры, что это действительно неопределенности.

24. Определение предела функии по Гейне. Равносильность определениюп о Коши (без доказательства).

Непрерывность,

25. Определение непрерывности в точке из области определения. Критерии непрерывности в предельной токе обла сти определения и в изолированной точке области определения. Непрерывность синуса. Классификация точек разрыва: устранимые, первого рода, второго рода. лекции + Шапошников стр 28 + Зорич стр 176-177 и стр 179, 181 и примеры далее]

26. Непрерывность композиции функций. Непрерывнсоть суммы, произведения, частного. Почему функция, «заданная формулой», непрерывна'

27. Непрерывные функции на отрезке. Теорема о промежуточных значениях, теорема Вейерширасса об ограниченности и теорема Вейерштрасса о достижеии супремума и инфинума. (Зорич 186-188]

Производная.

28. Внутренняя точка множества. Определение производной функции во внутренней точке. Определение дифференци-руемости функции в точке. Их равносильность. Левая и правая производные. [Шапошников, сгр 36-37.]
НЕПОЛНЫЙ ОТВЕТ
Точка х0 называется внутренней точкой множества E, если существует содержащий эту точку интервал (a,b) целиком содержащийся в множестве E

x0 ∈(a,b) ⊂E

Пусть y = f(x) определена в точке x₀ и некоторой ее окрестности.

Придадим x₀  приращение  Dx  такое, что  x₀ + DxÎD(f) . 

Функция при этом получит приращение 

Df(x₀) = f(x₀ + Dx)  – f(x₀) .

ТЕОРЕМА 1 (необходимое и достаточное условие существо-

вания производной). 

  Функция  y = f(x)  имеет производную в точке  x₀Û  в этой точке существуют и равны между собой производные функции справа и слева. Причем

ТЕОРЕМА 2 (необходимое условие существования производ-

ной функции в точке). 

  Если функция y = f(x)  имеет производную в точке  x₀ , то функция f(x)  в этой точке непрерывна.

Замечание. Непрерывность функции в точке  x₀  не является достаточным условием существования в этой точке производной функции. 

  Например, функция y = | x | непрерывна на всей области опре-

деления, но не имеет производной в точке  x₀ = 0.

Соответствие  x₀ ® f¢(x₀)  является функцией, определенной на множестве  D₁Í D(f). 

Ее называют производной функции  y = f(x) и обозначают

Операцию нахождения для функции  y = f(x)  ее производной функции называют дифференцированием функции  f(x).
29. Вычисление производной от хП , sin x, cos x по определению. (Зорич, стр 216-217]
30. Функция, имеющая производную в точке, непрерывная в этой точке. Пример, что обратное неверно. (Шапошников, середина стр 37.1

Теорема. Если функция  дифференцируема в некоторой точке  a, то она непрерывна в этой точке. Доказательство. По определению производной Это предельное равенство означает, что выражение под знаком предела можно представить в виде где  α(x)  – бесконечно малая функция при  x → a. Тогда Следовательно,    при  x → a. Заметим, что дифференцируемость функции в некоторой точке означает ее гладкость в окрестности этой точки, что влечет за собой непрерывность функции в рассматриваемой точке. Однако обратное утверждение несправедливо – функция, обладающая свойством непрерывности в некоторой точке, не обязательно дифференцируема в этой точке. Рис. 8. Непрерывная в точке a функция    не является дифференцируемой в этой точке.

31. Определение касательной. Критерий существования касательной. только лекции

32. Теорема о производной суммы, разности, произведения, частного. Производная от тангенса и котангенса. лекции + Зорич стр 227-228]

33. Теорема о производной композиции. [Шапошников, конец стр 38]



34. Вычисление производной от от ех и ах. Производная от хо для вещественного а [Шапошников, конец стр 39 + лекции

35. Теорема о производной обратной функции, вычисление производной от . [Зорич, стр 232-233 + замечание 1; производная от - только лекций

Теорема о производной обратной функции

Докажем теорему, позволяющую находить производную функции y=f(x), зная производную обратной функции.

Теорема. Если для функции y=f(x) существует обратная функция x=g(y), которая в некоторой точке у₀ имеет производную g '(v₀), отличную от нуля, то в соответствующей точке x₀=g(x₀) функция y=f(x) имеет производную f '(x₀), равную , т.е. справедлива формула .

Доказательство. Т.к. x=g(y) дифференцируема в точке y₀, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x₀=g(y₀). Следовательно, при Δx→0 Δy→0.

Покажем, что .

Пусть . Тогда по свойству предела . Перейдем в этом равенстве к пределу при Δy→0. Тогда Δx→0 и α(Δx)→0, т.е. .

Следовательно,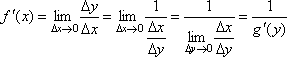

,

что и требовалось доказать.

Эту формулу можно записать в виде .

теперь пример: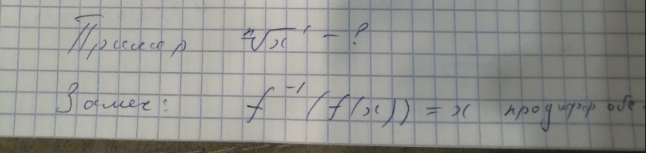


36. Теорема о производной обратной функции, вычисление производной от arcsin x. Зорич, стр 232-233 + замечание 1 + пример 10]



37. Теорема о производной обратной функции, вычисление производной от arctg x. [Зорич, стр 232-233 + замечание 1 + пример 111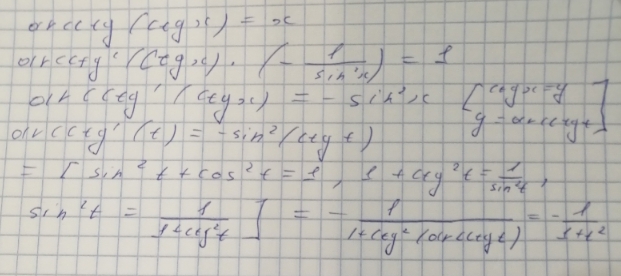



38. Теорема о производной обратной функции, вычисление производной от Inx и loga * [Зорич, стр 232-233 + замечание

1 + лекции

39. Точка локального экстремума. Теоремы Ферма и Ролля. Теорема Лагранжа. [Зорич, стр. 248- начало 252, со всеми примерами. В лекции чуть более простое док-во, и с мотивировкой.]

40. Производная и монотонность. Производная и строгая монотонность. Шапошников, стр 45 ИЛИ Зорич, стр 274-275]

41. Производная и локальные экстремумы: необходимое условие, достаточное условие через первую производную, до-статочное условие через вторую производную. [Лучше всего использовать лекции.1

42. Определеленеи выпуклости функции на интервале. Равносильность выпуклости тому, что угол наклона касательной возрастает. Шапошников, стр 46]

43. Критерий выпуклости и строгой выпуклости через первую и вторую производную. Определение выпуклости через касательную. Точки перегиба, как их искать. [Шапошников, стр 47. Примеры в Зориче на стр 285 п далее.]

44. Теорема Коши (обобщение т. Лагранжа). Правило Лопиталя для вычисления пределов. Доказательство только в самом простом случае.