47.Производная сложной и обратной функции
Теорема (о производной обратной функции)
Пусть функция 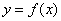 является непрерывной и строго монотонной в некоторой окрестности точки является непрерывной и строго монотонной в некоторой окрестности точки 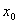 и имеет в этой точке производную и имеет в этой точке производную 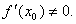 Тогда Обратная функция Тогда Обратная функция 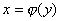 также имеет в соответствующей точке также имеет в соответствующей точке 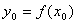 производную, причем производную, причем
Теорема (о производной сложной функции).
Пусть функция 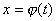 имеет производную в точке имеет производную в точке 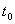 , а функция , а функция 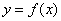 имеет производную в соответствующей точке имеет производную в соответствующей точке 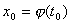 . Тогда сложная функция . Тогда сложная функция 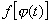 имеет Производную в точке имеет Производную в точке 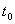 и справедлива следующая формула: и справедлива следующая формула:
48. Таблица производных
1.
|
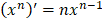
|
12.
|
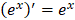
|
2.
|
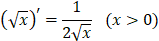
|
13.
|
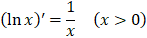
|
3.
|
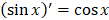
|
14.
|
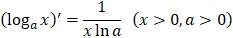
|
4.
|
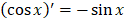
|
15.
|
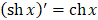
|
5.
|
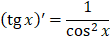
|
16.
|
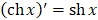
|
6.
|
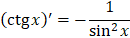
|
17.
|
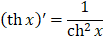
|
7.
|
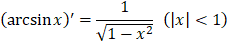
|
18.
|
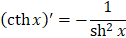
|
8.
|
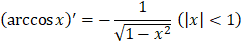
|
19.
|
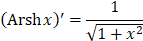
|
9.
|
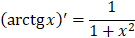
|
20.
|
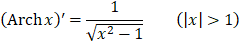
|
10.
|
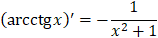
|
21.
|
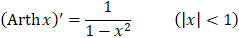
|
11.
|
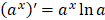
|
22.
|
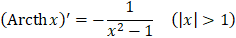
|
49.Производные высших порядков
Производная функции у = f (x) является также функцией: у'= f' (x).
Эта функция также может иметь производную. Эта новая производная называется второй производной функции у = f (x) или производной функции f (x) второго порядка и обозначается 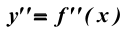 или или 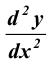 . .
Производная второй производной, то есть функции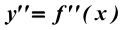 называется третьей производной или производной третьего порядка и обозначается символом называется третьей производной или производной третьего порядка и обозначается символом 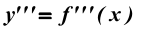 или или 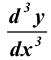 . Так можно ввести производные четвертого, пятого и вообще n-го порядка, которые обозначают . Так можно ввести производные четвертого, пятого и вообще n-го порядка, которые обозначают 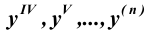
50.Дифференциал, определение и геометрический смысл. Основные теоремы о дифференциалах
Геометрический смысл дифференциала заключается в следующем: дифференциал функции f (x) равен приращению ординаты касательной к графику функции, которая проведена через некоторую точку с координатами (x, y) при изменении координаты x на величину Δх=dx.
Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х))
1)Дифференциал суммы, произведения и частного двух дифференцируемых функций определяются следующими формулами: 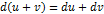 , , 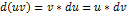 , , 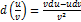
2)Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
51.Исследование функций при помощи производной . Некоторые теоремы о Дифференцируемых функциях.
Исследование функции на возрастание (убывание) и на экстремум удобно проводить с помощью производной. Для этого сначала находят производную функции f и ее критические точки, а затем выясняют, какие из них являются точками экстремума.
Теорема Ферма
|
Пусть функция y = f(x) определена в интервале (а, в) и принимает в точке с этого интервала наибольшее или наименьшее на (а, в) значение. Если существует f'(с), то f'(с) = 0.
Доказательство. Пусть, например, f(с)= М – наибольшее значение функции в интервале (а, в) и существует f'(с). По определению производной f'(с)=. При любом знаке Dх f(c+Dx)-f(c)≤0, так как f(с) – наибольшее значение функции в (а, в).
Если Dх>0, то и, следовательно, f'(с)≤0. Если же Dх<0, то и f'(с) ≥0. Следовательно, f'(с)=0.
Геометрически теорема означает, что касательная, проведенная к графику функции в точке (с; f(с)), параллельна оси Ох.
|
Теорема Ролля
|
Пусть функция y = f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (a, b) и f(a) = f(b) = 0. Тогда ее производная f'(х) обращается в нуль хотя бы в одной точке сÎ( a, b).
Доказательство. По условию функция y = f(x) непрерывна на отрезке [a, b], поэтому она достигает на [a, b] своего наибольшего М и наименьшего m значений. Если М = m, то функция постоянна на [a, b] и ее производная f'(х)=0 во всех точках (a, b). Пусть теперь М ¹ m, тогда хотя бы одно из этих чисел, например, m ¹ 0. Поэтому существует точка сÎ( a, b) такая, что f(с)= m. Следовательно, по теореме Ферма f'(с)=0.
Геометрически теорема означает, что если функция y = f(x) удовлетворяет теореме Ролля, то найдется хотя бы одна точка (с; f(с)), где сÎ(a;b), такая, что касательная к графику функции, проведенная в этой точке, параллельна осиОх.
|
Теорема Лагранжа
|
Пусть функция y=f(x) непрерывна на отрезке [a, b] и дифференцируема в интервале (a, b). Тогда существует хотя бы одна точка сÎ(a, b), для которой выполняется условие: .
Доказательство. Составим уравнение хорды АВ, соединяющей точки графика функции A(a; f(a)) и B(b; f(b)):
.
Отсюда ордината хорды у=. Рассмотрим функцию . Функция F(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b), так как функция f(x) непрерывна на [a, b] и дифференцируема на интервале (a,b). . Таким образом, функция F(x) удовлетворяет всем условиям теоремы Ролля. Поэтому существует такая точка сÎ(a, b), что , откуда получаем утверждение теоремы. Геометрически теорема Лагранжа означает, что существует хотя бы одна точка сÎ (а, b) такая, что касательная, проведенная к графику функции в точке (с; f (с)), параллельна хорде АВ.
|
Теорема Коши
|
Если функции f (х) и (х) непрерывны на отрезке [а, b] и дифференцируемы в интервале (а, b), причем , то существует точка сÎ (а, b) такая, что
Доказательство. Рассмотрим функцию
F(х) = [f(х)-f(а)] – . [(х)-(а)].
Легко проверить, что эта функция удовлетворяет теореме Ролля (аналогично тому, как это было сделано в предыдущей теореме). Следовательно, существует точка сÎ (a, b.) такая, что .
Отсюда получаем утверждение теоремы.
Замечание.
Равенства и
называются соответственно формулами Лагранжа и Коши.
|
51-52.
Теорема Лопиталя (Правило Лопиталя)
|
Пусть - функции, непрерывные на [а, b], дифференцируемые в(а, b); при всех хÎ (а, b) и f (а) = (а)=0.
Тогда, если существует , то существует ,причем = .
Доказательство. Возьмем на [а, b] какую-нибудь точку х а. Применяя формулу Коши, получим , где сÎ (а; х).
По условию f (а) = (а) = 0, значит . Если х а, то и са, так как сÎ (а, х).
При этом, если существует =А, то существует и = А.
Поэтому = = = = А.
Теорема доказана.
Замечание 1. Теорема имеет место и в том случае, если функции
f(х) и (х)не определены при х = а, но f(х)= 0,
(х)=0.
Замечание 2. Если и производные удовлетворяют всем тем условиям, которые наложены на функции в теореме Лопиталя, то применяя правило Лопиталя к отношению , получаем = и так далее. Теорема имеет место и в том случае, если f(х) и (х) не определены
при х = a, но f(х)= ∞, (х)= ∞, а также в случае а = ∞.
Таким образом, правило Лопиталя можно применять к неопределенностям вида .
| |
 Скачать 63.75 Kb.
Скачать 63.75 Kb.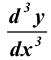 . Так можно ввести производные четвертого, пятого и вообще n-го порядка, которые обозначают
. Так можно ввести производные четвертого, пятого и вообще n-го порядка, которые обозначают 