Класс.шпор. Nсаныны гармоникалы ортасыны анытамасы
 Скачать 305.14 Kb. Скачать 305.14 Kb.
|
|
n-санының гармоникалық ортасының анықтамасы: а1,а2,...аn – сандарының гармоникалық орта мәні деп осы сандарға кері шамалардың арифметикалық орта мәніне кері шаманы айтады, демек 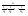 саны. саны. n- санының геометриялық ортасының анықтамасы: a1,a2,...,an сандарының геометриялық ортасы - a1,a2,...,an сандарының көбейтіндісінің n дәрежелі түбіріне тең 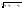 санын айтады. санын айтады.n-санының арифметикалық ортасының анықтамасы: арифметикалық орта – бірнеше санның (a1,a2,...,an) қосындысын қосылғыштардың санына (n) бөлгеннен шыққaн бөлінді сан 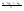 n-санының квадраттық ортасының анықтамасы: квадраттық орта –берілген а1,а2,...аn сандары квадраттарының арифметикалық орта шамасының квадрат түбіріне тең сан  Екі санның геометриялық және гармоникалық ортасы арасындағы теңсіздік. 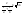 где где  Екі санның геометриялық және арифметикалық ортасы арасындағы теңсіздік. 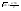 где где  Екі санның арифметикалық және квадраттық ортасы арасындағы теңсіздік. 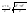 Коши-Буняковский теңсіздігі.a1,a2,…,an; b1,b2,…,bn (bi ≠ 0, i= 1,…,n) сандары үшін 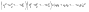 Теңсіздігі Коши-Буяновский теңсіздігі (Батыс басылымдарында бұл теңсіздікті Коши-Шварц теңсіздігі) деп аталады. Бұл теңсіздікте Теңсіздігі Коши-Буяновский теңсіздігі (Батыс басылымдарында бұл теңсіздікті Коши-Шварц теңсіздігі) деп аталады. Бұл теңсіздікте 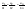 болғанда ғана, тек сонда ғана теңдік орындалады.Мұны француз математигі О.Коши дәлелдеген(1821). болғанда ғана, тек сонда ғана теңдік орындалады.Мұны француз математигі О.Коши дәлелдеген(1821).Бернулли теңсіздігі , егер х≥-1 болса , онда барлық n натурал мәндер үшін теңсіздік орындалады 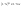 где где 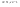 Симметриялық теңсіздіктің анықтамасы. Теңсіздік симметриялық деп аталады 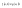 , егер мына теңдік орындалса , егер мына теңдік орындалса 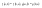 Чебышев теңсіздігі. 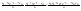 где где 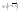 - оң сандар. - оң сандар. Ең тиімді алгоритм түсінігі. Пусть  и и  , тогда , тогда 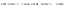 - этот алгоритм называется «жадным» алгоритмом. - этот алгоритм называется «жадным» алгоритмом.Математикалық индукция әдісі. Бізге мына түрдегі теңсіздікті дәлелдеу керек болсын:  При n=1 должно выполняться(теңсіздігі орындалуы керек) неравенство 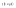 При n=k предполагаем выполнение(теңсіздікті дұрыс деп жорығанда) неравенства: 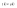 При n=k+1 , доказваем неравенство (теңсіздікті дәлелдейміз)  Үшбұрыш теңсіздіктері. a,b,c – АВС үшбұрышы қабырғаларының ұзындықтары болсын . Онда: a+b > c , a+c > b , b+c > a 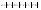 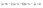 Бұл теңсіздіктер Үшбұрыш теңсіздіктері деп аталады. Йенсен теңсіздігі деп аталатын дөңес функциядағы n-нүктедегі мәндерінің арифметикалық ортасы мен осы нүктелердің арифметикалық ортасындағы функция мәнінің арасындағы қатынасты көрсететін теңсіздікті көптеген қиын олимпиадалық есептерді шығаруға қолдануға болады.Теорема: қандай да бір f(x) функциясы берілсін.Егер (а,b) кесіндісінде жататын  нүктелері үшін нүктелері үшін 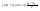 (1) теңсіздігі орындалса онда кез келген (1) теңсіздігі орындалса онда кез келген 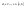 нүктелері үшінде нүктелері үшінде 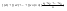 теңсіздігі орындалады. теңсіздігі орындалады.Юнга теңсіздігі. Tеріс емес екі a және b санын және p және q ( 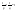 ) екі санын қарастырайық. Келесі Юнга теңсіздігін дәлелдейік: ) екі санын қарастырайық. Келесі Юнга теңсіздігін дәлелдейік: 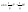 Дәлелдеу. Дәлелдеу. 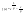 , , 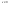 болғандағы функциясын қарастырайық. болғандағы функциясын қарастырайық. 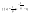 болғасын ,онда болғасын ,онда , ,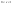 болғанда және болғанда және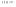 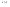 болған кезде. болған кезде.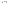 нүктесінде нүктесінде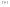 -функциясы ең үлкен мәнді қабылдайды, сонымен қоса -функциясы ең үлкен мәнді қабылдайды, сонымен қоса 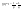 . Соған сәйкес, . Соған сәйкес, 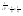 барлық барлық 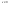 үшін.Соңғы теңсіздікте үшін.Соңғы теңсіздікте  . Осылайша Юнга теңсіздігі . Осылайша Юнга теңсіздігі  болғанда орындалады. болғанда орындалады. 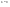 болған кезде ол анық. болған кезде ол анық.Гельдер теңсіздігі. a,b,p,q >0 және 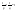 болсын. Сонда кез келген теріс емес а және b сандары үшін мына теңсіздік орынды: болсын. Сонда кез келген теріс емес а және b сандары үшін мына теңсіздік орынды: 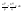  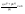 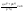  Минковский теңсіздігі. 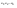 және және 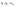 теріс емес сандар болсын және теріс емес сандар болсын және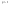 . Онда келесі Минковский теңсіздігі орынды . Онда келесі Минковский теңсіздігі орынды 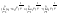 Дәлелдеу. 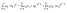 теңсіздігін жазып алайық. теңсіздігін жазып алайық.Егер 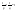  , онда , онда 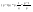 . Сондықтан . Сондықтан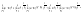 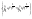 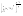 Соңғы теңсіздіктің екі жағын мынаған 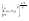 бөлсек, Минковский теңсіздігін аламыз. Герман Минковский (1864–1909)–немецкий математик бөлсек, Минковский теңсіздігін аламыз. Герман Минковский (1864–1909)–немецкий математикТеңсіздіктерді дәлелдеуде туындыны қолдану теореманың тұжырымдамасы. 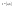 немесе немесе 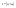 облысында облысында 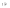 және және  функциялары анықталған және үзіліссіз. функциялары анықталған және үзіліссіз.Теорема. Егер 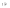 және және  функциялары функциялары  және және  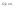 облыстарында дифференциалданатын болса , облыстарында дифференциалданатын болса ,  болса ,онда болса ,онда  -да теңсіздігі орынды: -да теңсіздігі орынды: 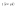 Егер 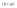  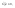 облыста , облыста ,  болса ,онда болса ,онда  -да -да 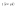 теңсіздігі орынды, теңсіздігі орынды, 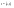 немесе немесе 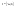 болған кезде. болған кезде.Теңсіздіктерді дәлелдеуде интегралды қолдану теореманың тұжырымдамасы. f(x) және g(x) интегралданатын болсын  және осы аралықта f(x) және осы аралықта f(x) g(x) теңсіздігі орындалады.Сонда g(x) теңсіздігі орындалады.Сонда  (1) Доказательство. (1) Доказательство. аралығында Т еркін белгіленген бөлінуін және f(x) және g(x) функциялары үшін тиісті интегралдық қосындысын қарастырамыз.олар үшін айқын қатынас жасалады. аралығында Т еркін белгіленген бөлінуін және f(x) және g(x) функциялары үшін тиісті интегралдық қосындысын қарастырамыз.олар үшін айқын қатынас жасалады. 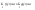 F(x) және g(x) үшін интегралдық қосындының тиісті бірізділігін және кездейсоқ қалыпты бөлу тізбегін қайта қарастыра отырып, (1)-ны аламыз. Екі оң санның гармоникалық және геометриялық ортасының арасындағы теңсіздіктің дәлелдемесі.Мысал: 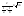 , ,  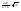 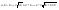 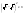 Екі теріс емес санның геометриялық және арифметикалық ортасының арасындағы теңсіздіктің дәлелдемесі.Мысал: 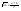 где где  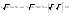 Екі теріс емес санның арифметикалық және квадраттық ортасының арасындағы теңсіздіктің дәлелдемесі.Мысал: 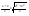 , ,  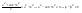 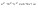 теңсіздігін дәлелдеудің қарапайым тәсілі. теңсіздігін дәлелдеудің қарапайым тәсілі.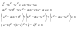 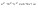 теңсіздігін Коши теңсіздігі арқылы дәлелдеңдер. теңсіздігін Коши теңсіздігі арқылы дәлелдеңдер.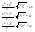 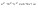 Симметриялығын пайдаланып 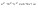 теңсіздігін дәлелдеу. теңсіздігін дәлелдеу.Так как неравенство является симметричным,предполагаем , что 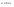 Применяя «жадный» алгоритм, получим: 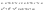 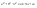 теңсіздігін Коши-Буняковский теңсіздігінің арқылы дәлелдеуі. теңсіздігін Коши-Буняковский теңсіздігінің арқылы дәлелдеуі.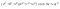 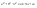 рассматривая разность 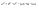 как функцию от переменной а . как функцию от переменной а .Рассмотрим функцию  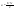 - min - min Коши-Буняковский теңсіздігінің дәлелдемесі. 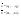 векторларын қарастырамыз векторларын қарастырамыз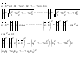 Чебышев теңсіздігінің дәлелдемесі. 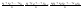  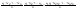 Бернулли теңсіздігінің дәлелдемесі. 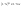 , ,  При n=1 1+x=1+x При n=k жорамалдаймыз, что 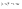 При n=k+1 үшін дәлелдейміз   Гельдер теңсіздігінің дәлелдемесі. Гельдер теңсіздігінің дәлелдемесі. a,b,p,q >0 және 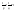 болсын. Сонда кез келген теріс емес а және b сандары үшін мына теңсіздік орынды: болсын. Сонда кез келген теріс емес а және b сандары үшін мына теңсіздік орынды: 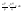  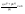 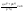  Минковский теңсіздігінің дәлелдемесі. 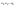 және және 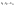 теріс емес сандар болсын және теріс емес сандар болсын және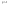 . Онда келесі Минковский теңсіздігі орынды . Онда келесі Минковский теңсіздігі орынды 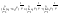 Дәлелдеу. 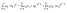 теңсіздігін жазып алайық. теңсіздігін жазып алайық.Егер 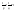  , онда , онда 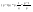 . Сондықтан . Сондықтан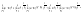 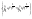 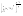 Соңғы теңсіздіктің екі жағын мынаған 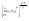 бөлсек, Минковский теңсіздігін аламыз. Герман Минковский (1864–1909)–немецкий математик бөлсек, Минковский теңсіздігін аламыз. Герман Минковский (1864–1909)–немецкий математикЙенсен теңсіздігінің дәлелдемесі. Йенсен теңсіздігі деп аталатын дөңес функциядағы n-нүктедегі мәндерінің арифметикалық ортасы мен осы нүктелердің арифметикалық ортасындағы функция мәнінің арасындағы қатынасты көрсететін теңсіздікті көптеген қиын олимпиадалық есептерді шығаруға қолдануға болады.Теорема: қандай да бір f(x) функциясы берілсін.Егер (а,b) кесіндісінде жататын 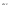 нүктелері үшін нүктелері үшін 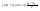 (1) теңсіздігі орындалса онда кез келген (1) теңсіздігі орындалса онда кез келген  нүктелері үшінде нүктелері үшінде  теңсіздігі орындалады. теңсіздігі орындалады.Юнга теңсіздігінің дәлелдемесі. Tеріс емес екі a және b санын және p және q (  ) екі санын қарастырайық. Келесі Юнга теңсіздігін дәлелдейік: ) екі санын қарастырайық. Келесі Юнга теңсіздігін дәлелдейік: 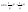 Дәлелдеу. 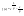 , ,  болғандағы функциясын қарастырайық. болғандағы функциясын қарастырайық. 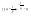 болғасын ,онда болғасын ,онда , ,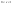 болғанда және болғанда және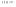  болған кезде. болған кезде. нүктесінде нүктесінде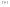 -функциясы ең үлкен мәнді қабылдайды, сонымен қоса -функциясы ең үлкен мәнді қабылдайды, сонымен қоса 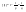 . Соған сәйкес, . Соған сәйкес, 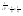 барлық барлық 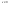 үшін.Соңғы теңсіздікте үшін.Соңғы теңсіздікте  . Осылайша Юнга теңсіздігі . Осылайша Юнга теңсіздігі  болғанда орындалады. болғанда орындалады. 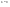 болған кезде ол анық. болған кезде ол анық.Теңсіздіктерді дәлелдеуде туындыны қолдану теоремасы. Дәлелдемесі. 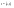 немесе немесе 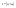 облысында облысында 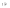 және және  функциялары анықталған және үзіліссіз. функциялары анықталған және үзіліссіз.Теорема. Егер 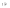 және және  функциялары функциялары  және және  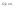 облыстарында дифференциалданатын болса , облыстарында дифференциалданатын болса ,  болса ,онда болса ,онда  -да теңсіздігі орынды: -да теңсіздігі орынды: 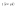 Егер 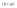  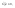 облыста , облыста ,  болса ,онда болса ,онда  -да -да 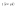 теңсіздігі орынды, теңсіздігі орынды, 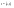 немесе немесе 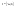 болған кезде. болған кезде.Теңсіздікті дәлелдеуде интегралды қолдану теоремасы.Дәлелдемесі f(x) және g(x) интегралданатын болсын  және осы аралықта f(x) және осы аралықта f(x)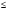 g(x) теңсіздігі орындалады.Сонда g(x) теңсіздігі орындалады.Сонда  (1) Доказательство. (1) Доказательство. аралығында Т еркін белгіленген бөлінуін және f(x) және g(x) функциялары үшін тиісті интегралдық қосындысын қарастырамыз.олар үшін айқын қатынас жасалады. аралығында Т еркін белгіленген бөлінуін және f(x) және g(x) функциялары үшін тиісті интегралдық қосындысын қарастырамыз.олар үшін айқын қатынас жасалады.  F(x) және g(x) үшін интегралдық қосындының тиісті бірізділігін және кездейсоқ қалыпты бөлу тізбегін қайта қарастыра отырып, (1)-ны аламыз. Математикалық индукция әдісін қолдана отырып, теңсіздіктерді дәлелдеу.Мысал келтіріңіз. 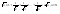 I) N=1 1=1 N=k 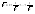 N=k+1 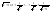 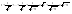 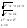 II) N=1 1<2  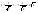 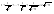 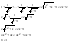 Айнымалыны ауыстыру әдісін қолдана отырып, теңсіздіктерді дәлелдеу.Мысал келтіріңіз. 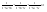 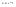 , , 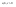 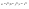 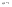 болсын. Бұдан болсын. Бұдан 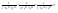 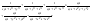 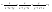 Тригонометриялық функцияларды қолдана отырып,теңсіздіктерді дәлелдеу. Мысал келтіріңіз. 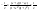 Дәлелдеу. Дәлелдеу. 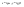 болсын. болсын. Бұдан 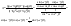 осыған сәйкес осыған сәйкес 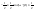 |
