Общее определение предела функции по Коши при произволь- ном стремлении аргумента. Расшифровка определения и геометри- ческая интерпретация предела для случаев: x a → − , x → ∞
|
Сформулировать теоремы: ( а) о предельном переходе в неравенстве; ( б) о пределе про- межуточной функции. Доказать одну из них
|
Дока- зать локальную ограниченность функции, имеющей конечный пре- дел и сформулировать теорему о замене переменной в пределе
|
|
|
|
Числовая последовательность. Определение предела последовательности, его геометрическая интерпретация. Сходящиеся после- довательности. Основные свойства предела последовательности. Доказать необходимое условие сходимости последовательности. Определение числа «е»
|
Сформули- ровать теоремы о локальных свойствах предела функции: ( а) о ло- кальной ограниченности функции, имеющей предел; ( б) о локальной знакоопределенности функции, имеющей предел, отличный от нуля (о сохранении функцией знака своего предела). Доказать одну из них
|
Определение производной функции в точке, ее геометрический и механический смысл. Определение дифференцируемости функции в точке. Доказать теорему о связи дифференцируемости и существо- вания конечной производной. Сформулировать теорему о связи дифференцируемости и непрерывности.
|
н
|
|
|
Дать определение функции, непрерывной в точке x0 , привести рав- носильные формулировки. Сформулировать локальные свойства функ- ции, непрерывной в точке х0
|
Сформулировать правило Лопиталя – Бернулли. Примеры. Дока- зать теорему о сравнении роста показательной, степенной и лога- рифмической функций при x → +∞
|
Определение экстремума функции. Доказать теорему Ферма (необходимое условие экстремума). Определение критической и стационарной точек функции. Сформулировать достаточное усло- вие экстремума
|
|
|
|
Определение бесконечно малой функции при данном стремлении аргумента. Расшифровка и геометрическая интерпретация для слу- чаев x a → + , x → +∞ . Доказать теоремы о связи функции, ее пре- дела и бесконечно малой при некотором стремлении аргумента. Сформулировать свойства бесконечно малых функций
|
Дать определение эквивалентности двух функций при данном стремлении. В качестве примера, из первого замечательного предела вывести эквивалентности (при x → 0 ) для функций tg x и 1− cos x
|
Сформулировать теорему о представлении функции по формуле Тейлора с остаточным членом в форме Пеано. Разложить функцию ln(1 ) + x по формуле Маклорена порядка n
|
|
|
|
Сформулировать теоремы: ( а) о предельном переходе в неравенстве; ( б) о пределе про- межуточной функции. Доказать одну из них
|
Дать определение эквивалентности двух функций. В качестве при- мера, из второго замечательного предела вывести эквивалентности (при x → 0 ) для функций ln(1 ) + x и 1 x a −
|
Сформулировать правила дифференцирования суммы, произведения и частного двух функций, теорему о производной сложной функции, теорему о производной обратной функции, доказать две из них
|
|
|
|
. Сформулировать теорему о «втором замечательном пределе» , до- казать её следствия
|
Определение дифференциала функции, его геометрический смысл. Сформулировать правила нахождения дифференциала сум- мы, произведения и частного двух функций. Доказать инвариант- ность формы первого дифференциала. Определение дифференциа- лов высших порядков.
|
Определение бесконечно малой функции при данном стремлении аргумента. Расшифровка и геометрическая интерпретация для случаев x a → − , x → −∞ .
|
|
|
|
Определение порядка малости (или роста) одной функции относи- тельно другой при данном стремлении аргумента. Привести примеры.
|
. Доказать теорему Коши. Сформулировать теорему Лагранжа, дать геометрическую интерпретацию этой теоремы
|
Сформулировать свойства бесконечно малых функ- ций. Доказать одно из них
|
|
|
|
Сформулировать арифметические теоремы о пределах (предел суммы, произведения и частного двух функций). Доказать одну из них.
|
Дать определение односторонней непрерывности функции в точ- ке. Сформулировать теорему о связи односторонней непрерывности с обычной (двусторонней).
|
Сформулировать и доказать теорему Ролля . Дать геометрическую интерпретацию этой теоремы.
|
|
|
|
Определение бесконечно большой функции при данном стремлении аргумента. Расшифровка и геометрическая интерпретация для случаев x a → + , x → ∞
|
Доказать теорему о связи бесконечно большой и бес- конечно малой функций.
|
. Определение непрерывности функции в точке. Дать эквивалентные формулировки. Сформулировать теорему о соответствующем свойстве элементарных функций
|
|
|
|
Доказать теорему Коши. Сформулировать правило Бернулли – Лопиталя.
|
Сформулировать теорему о пределе промежуточной функции. Доказать теорему о «первом замечательном пределе». Сформулиро- вать ее следствия.
|
Определение непрерывности функции на отрезке. Сформулиро- вать свойства функции, непрерывной на отрезке.
|
|
|
|
Сравнение функций при данном стремлении аргумента, определение отношений «» и «о-малое», примеры. Сформулировать теоремы об эквивалентных функциях. Доказать одну из них
|
Дать определение асимптоты графика функции. Сформулировать правила нахождения вертикальных, горизонтальных и наклонных асимптот графика функции y f x = ( )
|
Определение многочлена Тейлора в точке x0 для функции f x( ). Доказать теорему о нем (о значениях функции, многочлена Тейлора и их производных в точке 0 x ). Сформулировать теорему о предста- вимости функции по формуле Тейлора с остаточным членом в фор- ме Лагранжа.
|
|
|
|
Дать определение монотонности (возрастания, убывания) функции на интервале. Доказать достаточное условие и сформулировать необ- ходимое условие монотонности дифференцируемой функции.
|
Определение эквивалентных функций при данном стремлении. Сформулировать свойства отношения эквивалентности. Вывести эквивалентности для arcsin , ln(1 ) x x + и (1 ) 1 a + − x при x → 0
Применение эквивалентностей при вычислении пределов
|
Определение точки разрыва функции. Классификация точек раз- рыва. Примеры
|
|
|
|
Определение производной функции, её физический и геометриче- ский смысл. Вывести производные функций sin x и x a
|
Определение экстремума функции. Доказать необходимое условие экстремума. Определение критической и стационарной точек функции. Сформулировать достаточное условие экстремума в критической точ- ке.
|
Определение непрерывности функции в точке и на промежутке. Определение композиции функции и обратной функции. Сформу- лировать теоремы о непрерывности: (а) композиции двух функций; (б) обратной функции
|
|
|
|
Доказать теорему Лагранжа, дать её геометрическую интерпрета- цию.
|
Доказать теорему о «первом замечательном пределе». Сформули- ровать ее следствия. Доказать два из них.
|
Сформулировать свойства локального знакопостоянства функ- ции, имеющей предел, теоремы о предельном переходе в неравен- стве и о пределе промежуточной функции. Привести примеры.
|
|
|
|
Сформулировать общие свойства предела (о един- ственности, о локальной ограниченности и о локальном знакопостоян- стве) и доказать одно из них.
|
Определение функции, непрерывной на интервале и на отрезке. Сформулировать теоремы о свойствах функции, непрерывной на от- резке
|
Определение выпуклости функции (её графика) на промежутке. Доказать достаточное условие выпуклости графика
|
|
|
|
Определение точки перегиба графика. Доказать необходимое усло- вие перегиба графика в данной точке. Сформулировать достаточное условие перегиба.
|
Сравнение функций при данном стремлении аргумента, опреде- ление отношений «» и « о-малое», примеры. Сформулировать свой- ства отношения эквивалентности и необходимое и достаточное ус- ловие эквивалентности двух функций
|
Определение непрерывности функции в точке. Сформулировать теорему о переходе к пределу под знаком непрерывной функции и тео- ремы о непрерывности, связанные с суммой, произведением, частным и композицией двух функций
|
|
|
|
Определение асимптоты графика функции. Виды асимптот. Крите- рий существования горизонтальной и вертикальной асимптот. Вывести формулы для вычисления коэффициентов уравнения наклонной асим- птоты. Примеры
|
Определение дифференциала функции, его геометрический смысл. Сформулировать правила нахождения дифференциала сум- мы, произведения и частного двух функций. Доказать инвариант- ность формы первого дифференциала.
|
Определение дифференцируемости функции в точке. Доказать тео- ремы о связи дифференцируемости и: ( а) существования конечной производной; ( б) непрерывности функции в точке.
|
|
|
|
Дать общее определение предела функции при произвольном стремлении аргумента. Дать его расшифровку и геометрическую интерпретацию при x → −∞ и x a → +
|
Дать определение бесконечно малой функции. Сформулировать свойства бесконечно малых и доказать одно из них.
|
Сформулировать локальные свойства функций, имеющих конечный предел и доказать два из них.
|
|
|
|
Дать определение функции, непрерывной на отрезке. Сформулиро- вать свойства функций, непрерывных на отрезке. Привести примеры, показывающие существенность условий для выполнения этих свойств.
|
Дать определение локального экстремума функции. Сформулиро- вать первый и доказать второй достаточный признак экстремума
|
Доказать необходимое условие локального экстремума функции (теорему Ферма)
|
|
|
|
Дать определение эквивалентности бесконечно малых функций. Доказать эквивалентности для arcsin x и 1 cos − x при x → 0
|
Сформулировать теорему о втором замечательном пределе. Сформу- лировать следствия из нее и доказать два из них.
|
Доказать непрерывность функции f x x ( ) sin = . Определение элемен- тарной функции. Сформулировать теорему о связи понятий элементар- ная функция и непрерывная функция.
|
|
|
|
Дать определение точки перегиба функции. Сформулировать не- обходимое и доказать достаточное условие перегиба
|
Сформулировать теорему о разложении функции по формуле Тей- лора с остаточным членом в форме Лагранжа. Разложить функцию f x x ( ) sin = по формуле Маклорена.
|
Дать равносильные определения функции, непрерывной в точке. Сформулировать теорему о предельном переходе под знаком непре- рывной функции и теоремы о сохранении непрерывности относи- тельно арифметических операций, доказать одну из них
|
|
|
|
Дать определение предела числовой последовательности. Доказать необходимое условие сходимости и сформулировать достаточное ус- ловие сходимости последовательности
|
Сформулировать теорему о разложении функции по формуле Тейлора с остаточным членом в форме Пеано. Разложить функцию ( ) x f x e = по формуле Маклорена порядка n (вывод).
|
Дать определение дифференцируемости функции в точке. Доказать теорему о связи дифференцируемости и непрерывности функции.
|
|
|
|
Доказать теорему Коши. Вывести из нее теорему Лагранжа и дать ее геометрическую интерпретацию.
|
Дать общее определение предела функции при произвольном стремлении аргумента. Дать его расшифровку для случаев x a → и x → +∞ . Дать геометрическую интерпретацию
|
Дать определение односторонних пределов функции. Доказать тео- рему о связи односторонних пределов и предела функции
|
|
|
|
Доказать теорему о первом замечательном пределе. Сформулировать следствия из нее
|
Сформулировать правило Лопиталя – Бернулли раскрытия неопределенностей 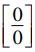 и и 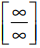 и доказать его для случая и доказать его для случая 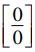
|
Сформулировать 1-й и 2-й достаточные признаки экстремума функ- ции. Доказать один из них.
|
|
|
|
 Скачать 23.98 Kb.
Скачать 23.98 Kb.