курс. Контрольная работа Структура и функционирование систем
 Скачать 349.38 Kb. Скачать 349.38 Kb.
|
|
Контрольная работа 1. Структура и функционирование систем Цель этой работы – получение навыков в выделении компонент системы, описание свойств и структуры системы, взаимодействия системы со средой, функционирования системы во времени и управления системой. Для выполнения задания обратитесь к материалам лекций 1, 2, 3. Задание: Выбрать систему для описания по своему желанию (это может быть информационная система, техническое устройство, организация, биологическая система., процесс, нацеленный на результат). Например: Система водоснабжения, транспортная система города, система выборов, банковская система, компьютерная сеть, человек, гостиница, предприятие, ресторан музей). Построить иерархическую структуру системы. Для этого выделить основные подсистемы исследуемого объекта. И в каждой подсистеме выделить входящие подсистемы и элементы. Представить иерархию в виде структурной схемы. Например. 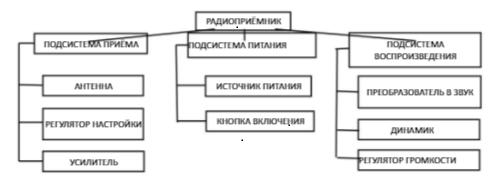 Рис. 1 Иерархическая система радиоприёмника. Опишите свойства системы и их проявление. Определите, какие свойства являются эмерджентными, а какие – нет. Обоснуйте свой выбор. Например: радиоприёмник производит звук, закодированный в виде радиоволн и посланный радиостанцией. Проявляется это свойство в звучании приёмника во время радиопередачи. Это эмерджентное свойство, так как отдельно ни один из элементов этой системы не обладает этим свойством: антенна только улавливает радиоволны и др… Опишите структуру системы и ее взаимодействие с окружающей средой. Определите те объекты окружающей среды, с которыми взаимодействует система. Опишите эти связи. Опишите и внутренние связи. 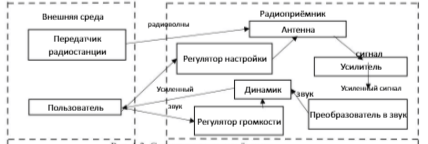 Рис. 2 Структура радиоприёмника Опишите функционирование системы и ее состояние при функционировании. Для этого выделите параметры системы (можно их сгруппировать по разным свойствам, например, физические или технические характеристики, экономические показатели и др.) Например, для технического устройства можно указать такие как материал, размер, стиль, параметры функционирования, также компанию-производителя, страну, марку, гарантийный срок, и др.)  Выделите из множества параметров те, которые характеризуют поведение (функционирование) системы, т.е. которые изменяются во времени. Опишите различные состояния системы и соответствующие значения параметров. Определите параметры в таблицу, например такую:
Укажите те параметры, которые вызывают переход системы из одного состояния в другое. Опишите возможности управления системой. Определите Цель системы. Если системы неживая, то ее цель определяет пользователь. Определите кто (что) и как управляет системой, с помощью каких управляющих воздействий осуществляется управление, используется ли в процессе управления обратная связь, если используется, то как? Составьте отчет, в который поместите титульный лист, последовательное описание всех этапов исследования, схемы и диаграммы, соответствующие каждому этапу. Задание 2. Проблема многокритериальности Теоретический материал с методикой решения типового примера В сложных системах анализ качества по одному показателю невозможен. Их качество определяется соответствием множеству требований к системе. То же самое можно сказать о проблеме оценки эффективности. Сложные системы многофункциональны, многорезультативны. Результативность и эффективность каждой из выполняемых функций также различна. Возникает векторная задача принятия решений. При рассмотрении векторных задач принятия решений в сложных системах используются понятия идеальной системы, а также понятие области адекватности. Система называется идеальной, если она идеально соответствует всем частных показателям. Будем обозначать вектор показателей для такой системы 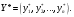 Областью адекватности назовем некоторую область, для которой нормированное значение каждого частного показателя отличается от идеального на некоторую допустимую величину. Областью адекватности назовем некоторую область, для которой нормированное значение каждого частного показателя отличается от идеального на некоторую допустимую величину.Однако возможны ситуации, когда сравниваемые системы являются наилучшими по одним показателям (характеристикам), но не лучшими по другим. Трудность принятия решения в таких ситуациях приводит к проблеме многокритериальности. Более того, проблема многокритериальности возникает, если требования к различным показателям противоречивы. Например, улучшение значения одного из показателей приводит к ухудшению значения других. Пусть имеется многокритериальная задача анализа систем с показателями для каждого 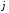 -го варианта системы: -го варианта системы: 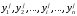 . Для простоты предположим, что все эти величины желательно максимизировать. Пусть в составе множества возможных вариантов систем есть два варианта систем такие, что все критерии . Для простоты предположим, что все эти величины желательно максимизировать. Пусть в составе множества возможных вариантов систем есть два варианта систем такие, что все критерии 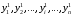 для первого решения больше или равны соответствующим критериям для второго варианта системы, причем хотя бы один из них действительно больше. Очевидно, тогда первый вариант лучше, чем второй, он вытесняет (доминирует) второй. Исключив его из рассмотрения, перейдем к сравнению других по всем показателям. В результате такой процедуры отбрасывания заведомо непригодных, невыгодных решений множество альтернативных вариантовобычно сильно уменьшается. В нем сохраняются только так называемые эффективные решения, характерные тем, что ни для одного из них не существует доминирующего решения. Такое множество недоминирующих вариантов называется множеством Парето. для первого решения больше или равны соответствующим критериям для второго варианта системы, причем хотя бы один из них действительно больше. Очевидно, тогда первый вариант лучше, чем второй, он вытесняет (доминирует) второй. Исключив его из рассмотрения, перейдем к сравнению других по всем показателям. В результате такой процедуры отбрасывания заведомо непригодных, невыгодных решений множество альтернативных вариантовобычно сильно уменьшается. В нем сохраняются только так называемые эффективные решения, характерные тем, что ни для одного из них не существует доминирующего решения. Такое множество недоминирующих вариантов называется множеством Парето.Проиллюстрируем прием выделения паретовских решений на примере задачи с двумя частными показателями: 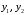 (оба требуется максимизировать). Множество альтернативных вариантов (оба требуется максимизировать). Множество альтернативных вариантов 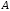 состоит из конечного числа состоит из конечного числа 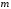 возможных решений возможных решений 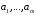 . Каждому решению соответствуют определенные значения частных показателей. Будем изображать решение точкой на плоскости с координатами . Каждому решению соответствуют определенные значения частных показателей. Будем изображать решение точкой на плоскости с координатами 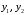 , и занумеруем точки соответственно номеру решения, как показано на рис.3.5. , и занумеруем точки соответственно номеру решения, как показано на рис.3.5.Очевидно, из всего множества 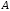 эффективными будут только решения, лежащие на правой верхней границе области возможных решений (см. жирные точки, соединенные отрезками прямой, на рис.3.5). Для всякого другого решения существует хотя бы одно доминирующее решение, для которого либо эффективными будут только решения, лежащие на правой верхней границе области возможных решений (см. жирные точки, соединенные отрезками прямой, на рис.3.5). Для всякого другого решения существует хотя бы одно доминирующее решение, для которого либо 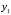 , либо , либо 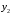 , либо оба больше, чем для данного решения. И только для решений, лежащих на правой верхней границе, доминирующих не существует. , либо оба больше, чем для данного решения. И только для решений, лежащих на правой верхней границе, доминирующих не существует. Рисунок 3.5. Множество Парето Когда из множества возможных решений выделены эффективные, то «переговоры» могут вестись уже в пределах этого «эффективного» множества. На рисунке его образуют четыре решения: 2, 3, 6, 11 из них 11—наилучшее по частному показателю 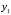 , 2—по частному показателю , 2—по частному показателю 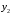 . Дело лица, принимающего решение, необходимо выбрать тот вариант, который для него предпочтителен и «приемлем» по обоим критериям. . Дело лица, принимающего решение, необходимо выбрать тот вариант, который для него предпочтителен и «приемлем» по обоим критериям.Пример 3.7. Рассмотрим пример построения множества Парето в случае синтеза системы, состоящей из двух блоков: блока А и блока B. Существует шесть возможных альтернативных вариантов выбора блока А (варианты блока А1-А6) и пять вариантов выбора блока В (варианты блока В1-В5). Каждый из блоков характеризуется двумя показателями: массой и стоимостью. Данные по альтернативам блоков приведены в табл.3.13. Таблица 3.13. Данные по альтернативам блоков
Столбец, указывающий на направление экстремума, указывает, что лучшей альтернативе соответствует меньшее значение показателя. Проведем попарное сравнение альтернатив для блоков А и В, начиная с альтернативы А1. Так, А1 лучше альтернативы А2 по первому показателю и хуже по второму. Таким образом, нельзя сказать, какая из этих альтернатив лучше. Однако, альтернатива А1 хуже альтернативы А3 по обоим показателям. Таким образом, альтернатива А1 должна быть исключена, как уступающая альтернативе А3. Продолжая анализ альтернатив, получим множество Парето для блока А, в которое входят третья и пятая альтернативы. Аналогично, оценивая альтернативы В1-В5, получим третью и четвертую альтернативы. Подобным образом строится множество эффективных решений и в случае, когда показателей не два, а больше (при числе их, большем трех, геометрическая интерпретация теряет наглядность, но суть дела сохраняется). Множество эффективных решений легче обозримо, чем множество 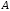 . Что касается окончательного выбора решения, то он по-прежнему остается прерогативой человека. . Что касается окончательного выбора решения, то он по-прежнему остается прерогативой человека. Часто при выборе альтернатив используют графические методы анализа. Например, может быть использована лепестковая диаграмма, которая входит в состав большинства программных средств обработки, в том числе и в состав офисного приложения Excel. Пример 3.8. Пусть нужно выбрать лучший персональный компьютер из пяти, данные по которым приведены в табл.3.14. Таблица 3.14. Данные по персональным ЭВМ
Понятно, что в данной таблице приведены данные только по некоторым показателям. Например, не указан размер монитора, его разрешение и др. Так как показатели имеют разную размерность и различный диапазон значений, для решения задачи выполним нормализацию показателей. Для этого используем нормализацию сравнения с помощью соотношения 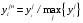 . Нормализованные значения параметров приведены в табл.3.15. . Нормализованные значения параметров приведены в табл.3.15.Таблица 3.15. Нормированные значения показателей
В силу того, что показатели, приведенные в табл.3.12, имеют разное направление экстремума, то вместо показателей, которые необходимо минимизировать будем использовать их дополнения до единицы. С учетом такого преобразования получим новые значения, приведенные в табл.3.16. Таблица 3.16. Преобразованные нормированные значения показателей
Построим лепестковую диаграмму, каждый луч которой соответствует одному преобразованному, нормированному показателю. Так как все показатели (с учетом преобразования) необходимо максимизировать, то чем больше площадь многоугольника, тем лучше альтернатива. На рис.3.6 приведена полученная лепестковая диаграмма. Судя по ней, лучшими является третья (ASUS X550CA) и пятая альтернативы (ASUS X550LA, M00430). 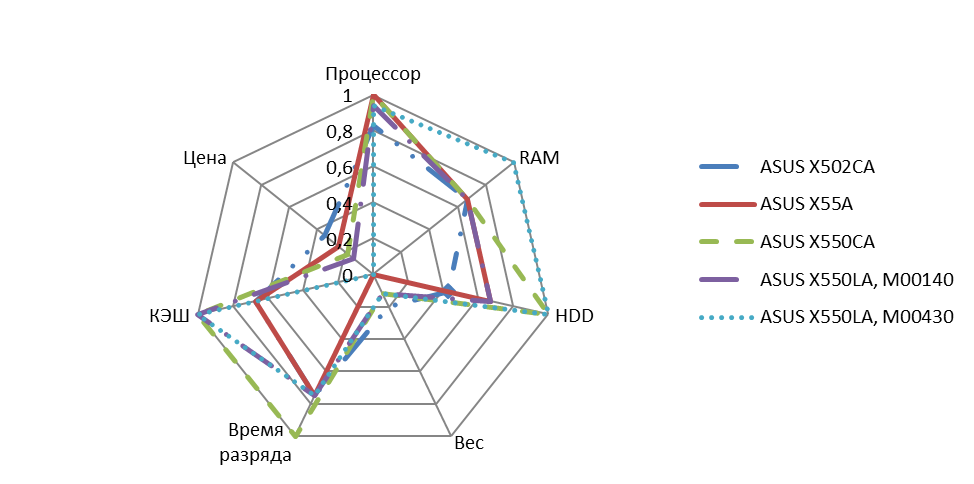 Рисунок 3.6. Лепестковая диаграмма Сама процедура выбора решения, будучи повторена неоднократно, может послужить основой для выработки некоторых формальных правил, применяемых уже без участия человека. Речь идет о так называемых «эвристических» методах выбора решений. Предположим, что опытный человек (или, еще лучше, группа опытных людей) многократно выбирает компромиссное решение в многокритериальной задаче при разных условиях. Набирая статистику по результатам выбора, можно, например, разумным образом подобрать значения «весов», в общем случае зависящие от условий и самих показателей 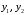 и воспользоваться таким обобщенным критерием для выбора решения, на этот раз уже автоматического, без участия человека. Рассмотрим три наиболее популярных метода решения многокритериальной задачи с учетом этого обстоятельства. и воспользоваться таким обобщенным критерием для выбора решения, на этот раз уже автоматического, без участия человека. Рассмотрим три наиболее популярных метода решения многокритериальной задачи с учетом этого обстоятельства.Самым популярным методом решения многокритериальной задачи является свертка критериев, переход к скалярному критерию, являющемуся функцией от частных показателей, входящих в состав векторного критерия. Часто с учетом допущения о попарной независимости частных показателей используется аддитивный 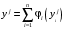 или мультипликативный критерии или мультипликативный критерии 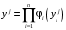 . В простейшем случае, с учетом процедуры нормализации, данные критерии имеют вид . В простейшем случае, с учетом процедуры нормализации, данные критерии имеют вид 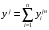 или или 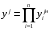 . . Если отдельные показатели имеют разные направления оптимизации, то для учета этих направлений при использовании аддитивной свертки целесообразно вводить знак. Когда показатели следует максимизировать, то каждый показатель следует брать со знаком «плюс». При минимизации показателя, в его свертку следует включать со знаком «минус». В том случае, если будем использовать мультипликативную свертку, то показатели, которые следует максимизировать, будем размещать в числителе дроби, а показатели, которые следует минимизировать, - в ее знаменателе. Пример 3.9. Еще раз рассмотрим пример выбора персонального компьютера. Для выбора лучшего компьютера будем использовать аддитивную и мультипликативную свертки. Результаты таких сверток приведены в табл.3.17. Таблица 3.17. Результаты аддитивной и мультипликативной свертки
Судя по таблице, как для аддитивной, так и для мультипликативной сверток критерии имеют максимальное значение для третьей альтернативы. Близкое значение имеет пятая альтернатива. Приведенный пример показывает инвариантность результатов к виду свертки. Вместе с тем, аддитивный критерий проще и имеет более ясную интерпретацию. Поэтому, как правило, используют аддитивную свертку. Пример 3.10. Вновь решим проблему выбора персонального компьютера с учетом весов показателей. При определении весов показателей будем использовать метод Черчмена-Акоффа. В качестве наиболее важного выберем показатель цены. Упорядочим по убыванию важность показателей: 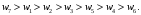 Примем значение наиболее важного показателя равным единице; Примем значение наиболее важного показателя равным единице; 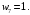 Другие веса приведены в табл.3.18. Другие веса приведены в табл.3.18.Таблица 3.18. Веса показателей
Сравним полученные значения весов по предпочтительности по отношению к самому приоритетному с целью корректуры оценок, приведенных в таблице. Пусть 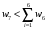 . Будем исключать частные показатели. Предположим, что в результате такого исключения остались только два показателя. Их веса приведены в правой части неравенства, . Будем исключать частные показатели. Предположим, что в результате такого исключения остались только два показателя. Их веса приведены в правой части неравенства, 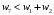 . Начальные значения весов соответствуют этому неравенству. . Начальные значения весов соответствуют этому неравенству. Выберем для дальнейшего анализа второй по важности показатель, показатель 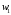 . Продолжим оценку весов по предпочтительности по отношению к этому показателю. Пусть . Продолжим оценку весов по предпочтительности по отношению к этому показателю. Пусть 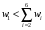 . Предположим, что последовательно, исключая отдельные показатели, получим . Предположим, что последовательно, исключая отдельные показатели, получим 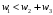 . . Затем рассмотрим следующий показатель 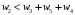 . Пусть, однако . Пусть, однако 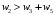 . Следовательно, нужно выполнить корректуру весов. Примем . Следовательно, нужно выполнить корректуру весов. Примем 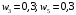 . Проанализируем следующий по важности показатель. Будем считать, что . Проанализируем следующий по важности показатель. Будем считать, что 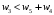 . Будем считать, что вместе с тем, . Будем считать, что вместе с тем, 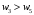 . Выполним корректуру веса, получим . Выполним корректуру веса, получим 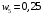 . . Анализируя следующий показатель, пусть получим 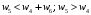 . Для обеспечения данного неравенства выполним корректуру веса. Пусть . Для обеспечения данного неравенства выполним корректуру веса. Пусть 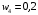 . Объединим полученные значения весов в таблицу, и затем нормируем веса так, чтобы . Объединим полученные значения весов в таблицу, и затем нормируем веса так, чтобы 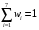 . Итоговые значения весов сведены в табл.3.19. . Итоговые значения весов сведены в табл.3.19.Таблица 3.19. Итоговые значения весов показателей
С учетом полученных значений весов найдем значения критериев для случая аддитивной свертки. Полученные значения приведены в табл.3.20. Таблица 3.20. Результаты аддитивной свертки с учетом весов показателей
Результаты выполненной свертки значений показателей показывают, что вновь лучшими являются третья и пятая альтернативы. Для приведенного примера мультипликативную свертку использовать не целесообразно, т.к. есть нулевые значения показателей. Поэтому при умножении на них будет получено нулевое значение критерия. Мультипликативную свертку можно использовать, если выполнить нормализацию частных критериев по другим правилам, например с помощью нормализации усреднения. Нормализованные значения для этого правила нормализации приведены в табл.3.21. Таблица 3.21. Нормализованные значения после использования нормализации усреднения
Для такой нормализации можно выполнить как аддитивную, так и мультипликативную свертки. При этом для случая аддитивной свертки те показатели, которые необходимо максимизировать, возьмем со знаком «плюс», а те, которые необходимо минимизировать – со знаком «минус». Для мультипликативного критерия те показатели, которые следует максимизировать, поместим в числитель, а те, которые следует минимизировать – в знаменатель свертки. Полученные результаты аддитивной и мультипликативной свертки приведены в табл.3.22. Таблица 3.22. Результаты аддитивной и мультипликативной свертки
Вновь третий и пятый компьютеры как для аддитивной, так и для мультипликативной сверток являются наилучшими. Учитывая значения в таблице 3.22, окончательно выбираем третий компьютер. При достаточно большом N применение метода Черчмена-Акоффа становится слишком трудоемким. В этом случае целесообразно разбить альтернативы на группы, а одну из альтернатив, например максимальную, включить во все группы. Это позволяет получить численные оценки всех альтернатив с помощью оценивания внутри каждой группы. В некоторых случаях очень полезной оказывается процедура выбора решения в так называемом «диалоговом режиме», когда компьютер, произведя расчеты, выдает значения показателей 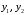 ,..., а это человек, критически оценив ситуацию, вносит изменения в весовые коэффициенты (или иные параметры управляющего алгоритма), выполняя, таким образом, балансировку модели. ,..., а это человек, критически оценив ситуацию, вносит изменения в весовые коэффициенты (или иные параметры управляющего алгоритма), выполняя, таким образом, балансировку модели. Другим, часто применяемым методом сведения многокритериальной задачи к однокритериальной, является метод главного показателя. Для этого, следует выделить один (главный) показатель 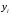 и стремиться его обратить в максимум (минимум). На все остальные показатели нужно наложить только некоторые ограничения, потребовав, чтобы они были не меньше (не больше) каких-то заданных значений (т.е. чтобы они принадлежали области адекватности). Например, при оптимизации плана работы предприятия можно потребовать, чтобы прибыль была максимальна, план по ассортименту — выполнен или перевыполнен, а себестоимость продукции была не выше заданной. При таком подходе все показатели, кроме одного — главного, переводятся в разряд заданных условий. Известный произвол в назначении границ, разумеется, при этом остается; поправки в эти границы тоже могут быть введены в «диалоговом режиме». и стремиться его обратить в максимум (минимум). На все остальные показатели нужно наложить только некоторые ограничения, потребовав, чтобы они были не меньше (не больше) каких-то заданных значений (т.е. чтобы они принадлежали области адекватности). Например, при оптимизации плана работы предприятия можно потребовать, чтобы прибыль была максимальна, план по ассортименту — выполнен или перевыполнен, а себестоимость продукции была не выше заданной. При таком подходе все показатели, кроме одного — главного, переводятся в разряд заданных условий. Известный произвол в назначении границ, разумеется, при этом остается; поправки в эти границы тоже могут быть введены в «диалоговом режиме».Существует еще один путь построения компромиссного решения, который можно назвать «методом последовательных уступок». Предположим, что показатели 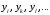 расположены в порядке убывания их важности. В данном методе сначала ищется решение, обращающее в максимум первый (важнейший) показатель. Затем назначается, исходя из практических соображений, с учетом малой точности, с которой нам известны входные данные, некоторая «уступка» расположены в порядке убывания их важности. В данном методе сначала ищется решение, обращающее в максимум первый (важнейший) показатель. Затем назначается, исходя из практических соображений, с учетом малой точности, с которой нам известны входные данные, некоторая «уступка» 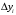 , которую можно сделать для того, чтобы максимизировать второй показатель , которую можно сделать для того, чтобы максимизировать второй показатель 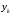 . Затем делается уступка для следующего показателя и т.д. . Затем делается уступка для следующего показателя и т.д.ЗАДАНИЕ Примените освоенную методику для выбора претендента на должность водителя (со своим автомобилем). К исходной таблице 3.23 добавьте столбец, в котором укажите: к минимуму или максимуму должен стремиться показатель(критерий). Таблица 3.23 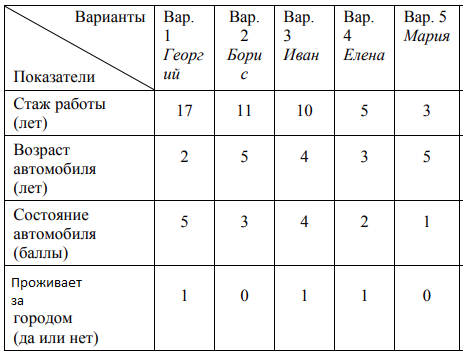 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
