ЭЛЕКТРОНИКА. КР5_ЦОС_СЕМЕНИХИНА_ЕЛИЗАВЕТА_ИБ3_3КУРС. Контрольные вопросы 5 Что значит сходимость zпреобразования
 Скачать 31.8 Kb. Скачать 31.8 Kb.
|
|
Контрольные вопросы 5 Что значит сходимость z-преобразования? Cходимость z-преобразования: Если F(z) содержит бесконечное число слагаемых, то ряд сходится в области 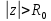 при условии при условии 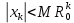 , где M>0, , где M>0, 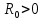 - вещественные константы. - вещественные константы.В области 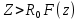 - аналитическая функция, не имеющая полюсов и существенно особых точек. - аналитическая функция, не имеющая полюсов и существенно особых точек.Что такое полюс в z- пространстве? Значения z, для которых S(z) = ∞, называются полюсами. К чему приведет Умножение z-образа сигнала s(k) на величину zn? К задержке сигнала (сдвиг вправо по временной оси) на n интервалов: znS(z) s(k-n) Характерные точки комплексной z-плоскости Подстановка значения какой-либо частоты в z = exp(-jtω) отображается точкой на окружности. Частоте 0 соответствует точка Re z = 1 и Im z = 0 на правой стороне оси абсцисс. При повышении частоты точка смещается по окружности против часовой стрелки, и занимает крайнее левое положение на частоте Найквиста. Отрицательные частоты спектра отображаются аналогично по часовой стрелке на нижней полуокружности. Точки 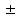 N совпадают, а при дальнейшем повышении или понижении частоты значения начинают повторяться в полном соответствии с периодичностью спектра дискретной функции. Проход по полной окружности соответствует одному периоду спектра, а любая гармоника спектра сигнала задается на плоскости двумя точками, симметричными относительно оси абсцисс. N совпадают, а при дальнейшем повышении или понижении частоты значения начинают повторяться в полном соответствии с периодичностью спектра дискретной функции. Проход по полной окружности соответствует одному периоду спектра, а любая гармоника спектра сигнала задается на плоскости двумя точками, симметричными относительно оси абсцисс.Куда входит единичная окружность |z| = |exp (-jω)| = 1если функция s(t) имеет спектральное представление S(ω) ? Если функция s(t) имеет спектральное представление S(ω), то единичная окружность |z| = |exp (-jω)| = 1 обязательно должна входить в область сходимости полинома S(z). Докажите, что для импульса Кронекера Xδ(z) = z0 =1 Импульсы Кронекера. В общем случае, для импульса Кронекера в произвольной точке числовой оси: (k-n) при k=n, (k-n) = 0 при k ≠ n. X(z) = 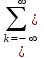 (k-n) zk = zn. (k-n) zk = zn.Для импульса Кронекера в нулевой точке соответственно X (z) = z0 =1. Ряд X (z) сходится на всей z-плоскости. Основные свойства Z-ПРЕОБРАЗОВАНИЯ. Линейность: Если s(k) = a·x(k)+b·y(k), то S(z) = aX(z)+bY(z). Соответственно, z-преобразование допустимо только для анализа линейных систем и сигналов, удовлетворяющих принципу суперпозиции. Задержка на n тактов: y(k) = x(k-n). Y(z) = 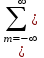 x(m) zm = zn X(z). x(m) zm = zn X(z).Соответственно, умножение z-образа сигнала на множитель zn вызывает сдвиг сигнала на n тактов дискретизации. Дифференцирование. Если имеем s(k) S(z), то z-образ функции ks(k) можно найти, продифференцировав S(z), что бывает полезно для вычисления обратного z-преобразования функций S(z) с полюсами высокого порядка: ks(k) z dX(z)/dz. Преобразование свертки. При выполнении нерекурсивной цифровой фильтрации односторонними операторами фильтров: s(k) = 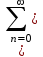 h(n) y(k-n), k = 0, 1, 2, … h(n) y(k-n), k = 0, 1, 2, …Z-преобразование уравнения свертки: S(z) = 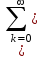 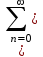 h(n) y(k-n) zk = h(n) y(k-n) zk =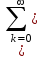 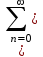 h(n) zn y(k-n) zk-n = h(n) zn y(k-n) zk-n == 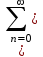 h(n) zn h(n) zn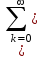 y(k-n) zk-n = H(z) Y(z). y(k-n) zk-n = H(z) Y(z).Таким образом, свертка дискретных функций отображается произведением z-образов этих функций. Аналогично, для z-преобразования могут быть доказаны все известные теоремы о свойствах z-образов, что вполне естественно, т.к. при z=exp(-j) эти свойства полностью эквивалентны свойствам спектров функций. Какие нули и полюсы оказывают наибольшее влияние на изменение АЧХ по частоте? Наибольшее влияние на изменение АЧХ по частоте оказывают нули и полюсы, расположенные ближе к единичной окружности. При расположении нуля непосредственно на окружности гармоника s в этой точке полностью обнуляется. И, наоборот, при перемещении s к полюсу, близкому к единичной окружности, происходит резкое нарастание коэффициента усиления системы. Чем определяется гладкость разложения H(z) (разрешение по частоте ∆f = 1/(N∆t)) при БПФ? Гладкость (разрешение по частоте f = 1/(Nt)) будет определяться количеством коэффициентов степенного ряда и при необходимости может увеличиваться дополнением ряда нулями. Где находятся полюсы передаточной функции H(z) устойчивой системы? В устойчивой системе все полюсы передаточной функции H(z) должны находиться за границами единичной окружности z=exp(-jt) (внутри окружности при символике z-1). |
