лаба100. гаджиев. Контрольные вопросы Какие измерения называются прямыми косвенными
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
Среднее арифметическое | Сумма (с учетом знаков) отклонений от среднего арифметического | Сумма квадратов отклонений от среднего арифметического | ||||||
| | | 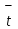 = =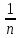 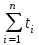 = 4,984 с = 4,984 с | 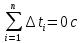 | 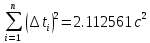 | ||||
| j | tлев(min) | tпр(max) | ∆nj | ∆nj /n |
| 1 | 4,464 | 4,617 | 1 | 0,014 |
| 2 | 4,617 | 4,770 | 4 | 0,056 |
| 3 | 4,770 | 4,923 | 16 | 0,222 |
| 4 | 4,923 | 5,076 | 33 | 0,458 |
| 5 | 5,076 | 5,229 | 13 | 0,181 |
| 6 | 5,229 | 5,382 | 5 | 0,069 |
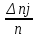 =
=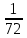 = 0,014
= 0,014 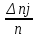 =
=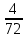 = 0,056
= 0,056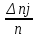 =
=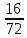 = 0,222
= 0,222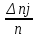 =
=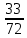 = 0,458
= 0,458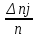 =
=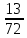 = 0,181
= 0,181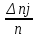 =
=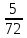 = 0,069
= 0,069Строим гистограмму экспериментальных значений и кривую закона распределения:
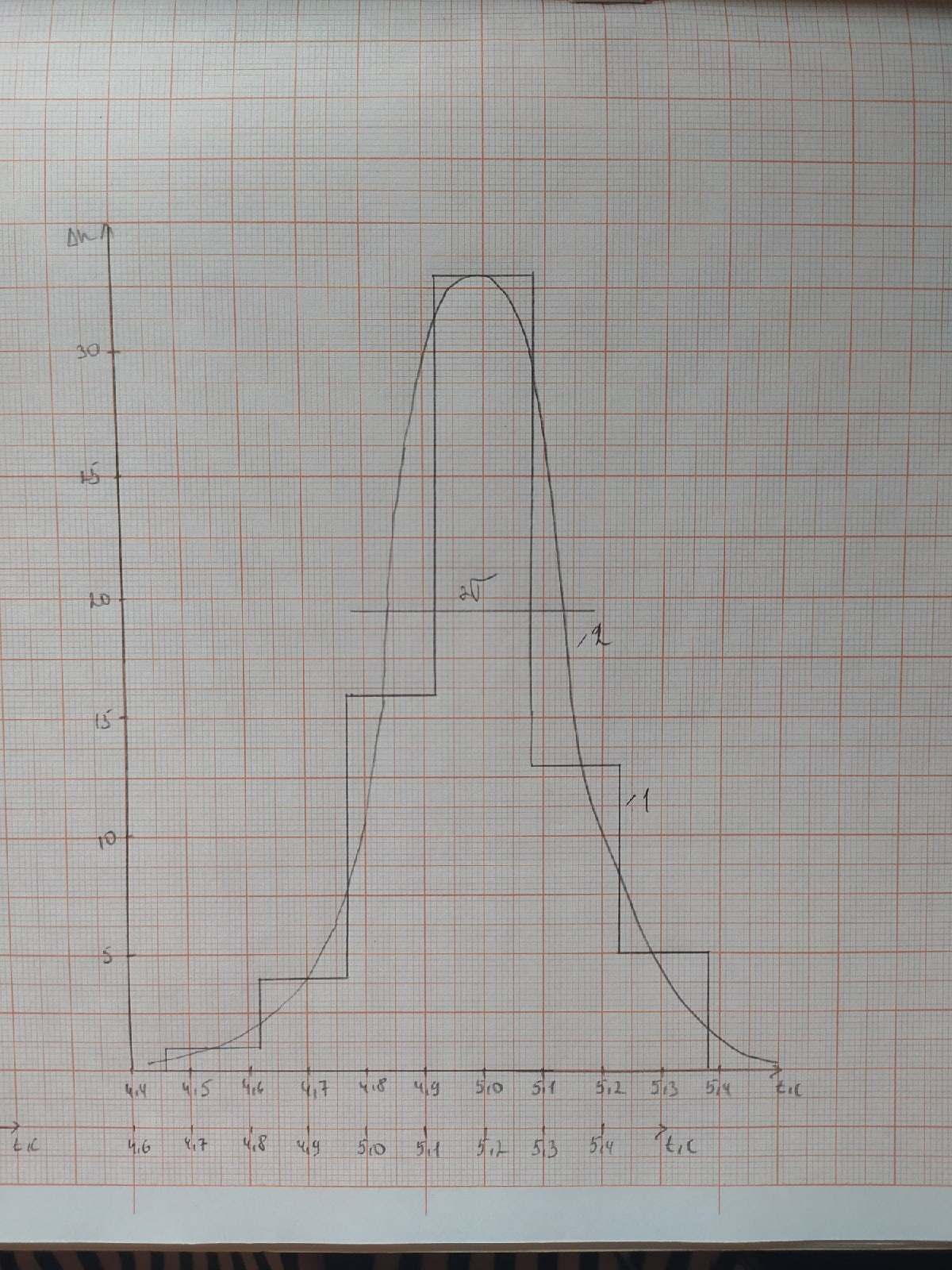
Гистограмма экспериментальных значений (1)
и кривая закона распределения ∆n/n (2)
На уровне 0.6 от максимального значения находим ширину кривой закона распределения :
2
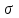
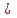 0,350
0,350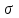 =
=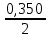
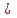 0,170 с
0,170 сВеличина
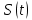 соответсвует величине
соответсвует величине 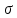 в пределах погрешности
в пределах погрешностиВывод:
А) В ходе лабораторной работы был построен график зависимости результатов наблюдений от порядкового номера наблюдения. Проанализировав его, можно заключить, что дрейф отсутствует
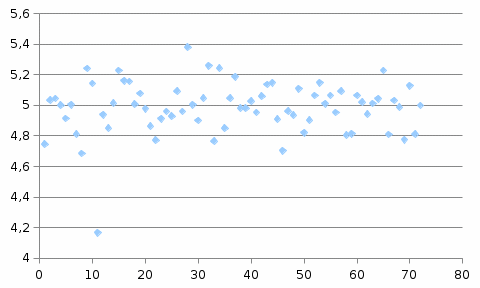
Б) Измерили длительность промежутка времени:
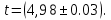 Полученное значение соответствует данному в пределах погрешности
Полученное значение соответствует данному в пределах погрешностиB) Полученная выборка соответствует гауссову закону распределения

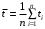
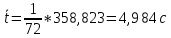
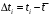
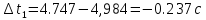
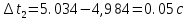
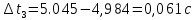
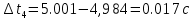
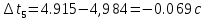
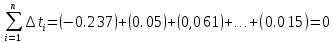
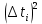 и сумму
и сумму 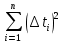
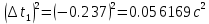
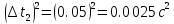
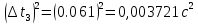
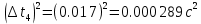
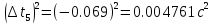
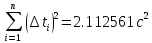
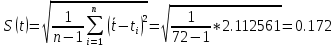
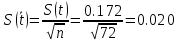
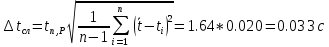
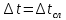
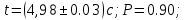
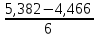 = 0,153
= 0,153