Программист. Контрольные вопросы (задания) к зачету, 4 семестр
 Скачать 96.01 Kb. Скачать 96.01 Kb.
|
|
Контрольные вопросы (задания) к зачету, 4 семестр: 1 Постановка и элементы задачи принятия решений. Участники процесса принятия решений В общем виде постановка задачи при- нятия решения включает следующую пару элементов [23]: где X — некоторое множество альтернатив, т. е. вариантов, из которых требуется сделать выбор; Ω — некоторый принцип оптимальности, крите- рий выбора, позволяющий сравнить альтернативы и выбрать из них наи- лучшую. Заметим, что альтернатива будет наилучшей именно в смысле за- данного критерия. Если принять другой критерий, то эта альтернатива, напротив, может быть далеко не самой лучшей. Обычно критерий отра- жает точку зрения лица, принимающего решение (ЛПР). Пусть, например, Х есть множество экзаменационных билетов. Положим, что ЛПР-студент обладает свободой выбора, т. е. может сравнить и выбрать любой би- лет х — элемент из множества Х. Можно предположить, что оптимальной альтернативой х* для данного ЛПР будет та, которая удовлетворяет крите- рию минимизации сложности вопросов в билете: х*: F (х*) → min, где F (.) — некоторый показатель, характеризующий уровень сложности вопроса. В соответствии с принятым критерием выбирается тот билет х*, значение F (х*) для которого меньше, чем значение F (х) для всех осталь- ных билетов x ∈ X. Для ЛПР-преподавателя критерием выбора будет некоторый другой. В простом случае можно положить, что желания данного ЛПР противо- положны желаниям студента и выражаются критерием F (х*) → max (та- кая постановка задачи сугубо иллюстративна и не претендует на отра- жение истинных целей преподавателя на экзамене). Очевидно, что новое ЛПР выберет по этому критерию для студента совершенно другой билет. Отметим, что в любом случае предполагается наличие самой воз- можности выбора. Эта возможность выбора является необходимым условием существования задачи принятия решения, т. е. в постановке за- дачи предполагается, что, во-первых, X содержит более одного элемента; во-вторых, любые из этих элементов доступны для выбора. В широком смысле слова процесс принятия решения включает не только этап выбора, но и такие этапы, как: • разработка альтернатив (определение множества Х); • выбор показателей для отражения наиболее важных свойств аль- тернатив и формирование критерия выбора альтернатив; • анализ и сравнение альтернатив по данному критерию; • собственно принятие решения (выбор альтернативы); • реализация принятого решения и контроль за исполнением ре шения. Последний этап наиболее характерен для процессов принятия реше ний в системах управления предприятиями, где исполнение решений воз- лагается на соответствующих работников и является достаточно продол- жительным и трудоемким самостоятельным процессом. В зависимости от того, каким образом заданы элементы ЗПР, на сколько формализованы условия, может быть введена классификация этих задач. При этом для каждого класса разрабатываются и применяют- ся свои методы решения В процессе принятия решения выделяются следующие основные участники: • лицо, принимающее решение — человек или коллектив, облада- ющие возможностями и полномочиями для принятия решения, которые осуществляют выбор и несут ответственность за приня- тое решение. При принятии решения ЛПР руководствуется не- которыми целями как объективного, так и субъективного свой- ства. Последнее говорит о том, что ЛПР делает выбор с учетом собственных предпочтений и интересов; • эксперт — человек, который является высококвалифициро- ванным специалистом в данной предметной области, имеет опыт и положительные результаты практической деятель- ности, обладает возможностями и желанием, позволяющими провести информационную подготовку процесса принятия решения. В задачи такой подготовки входит, в частности, оценка характеристик и предварительный анализ альтерна- тив. Эта информация используется ЛПР при принятии реше- ния. В число задач экспертов могут также входить формиро- вание множества альтернатив, участие в выборе показателей и критериев, выработка аналитических рекомендаций и т. п. Отметим еще раз, что, несмотря на значительную роль экспер- тов в ЗПР, собственно выбор и ответственность за него оста- ются прерогативой ЛПР. 2 Классификация ЗПР: задача оптимизации, задача выбора, общая задача. 1. Задача выбора. Множество альтернатив Х задано явно, т. е. путем перечисления альтернатив, а Ω задан в виде критерия, позволяющего сравнить альтернативы из Х между собой. Критерий может быть простым или сложным, т. е. состоять из нескольких более простых критериев. 2. Задача оптимизации. Множество Х задано математически (неявно), с помощью набора условий, ограничивающих подмножество допустимых решений в пространстве параметров; Ω, т. е. критерий выбора (критерий оптимизации) тоже задается математически — в виде целевой функции, которая показывает зависимость нужного свойства от сочетания параме- тров системы. Такая задача может быть записана в следующем виде (см. также разд. 4.4): f = f (X) → max (min) gj (X) ≤ (≥, =) bj, j = 1, 2, 3, ..., m, (5.1)где f(X) — целевая функция, показывающая зависимость критерия от зна- чений параметров x1, x2, …; gj (X) ≤ (≥, =) bj — условия, которые ограничивают в пространстве параме- тров те точки Х = (x1, x2, …), которые являются допустимыми решениями. Решение задачи приводит к нахождению такой точки Х* = (x1*, x2*, …), которая лучше других по заданному критерию. Простым примером ЗПР такого класса является задача линейного программирования, рассмотренная в гл. 4. Очевидно, что в задачах 2-го класса возможных решений может быть гораздо больше, чем в задачах 1-го класса. На самом деле, если параме- тры х есть действительные числа, таких решений будет бесконечно много. В то же время в силу высокой степени формализации для поиска решения в этих задачах могут быть применены известные математические методы и алгоритмы, позволяющие автоматизировать процесс поиска Х*. В системном анализе чаще встречаются более сложные задачи этого класса, в которых критерий не один, а несколько. Такие задачи называют- ся многокритериальными. 3. Общая задача принятия решений. Здесь Х и Ω не заданы ни путем перечисления, ни в виде математической формулы. В то же время имеют- ся некоторые представления о допустимости и оптимальности решений. Причем эти представления являются, как правило, субъективными, отра- жают личный опыт и предпочтения различных участников процесса при- нятия решений. Задача требует определения или генерации множества Х, а также определения (если это возможно) критериев выбора. В системном анализе на разных этапах исследования приходится сталкиваться со всеми перечисленными классами задач. Так от задачи 3-го класса можно перейти к задаче выбора, если удается перечислить аль- тернативы, т. е. определить Х, а критерий выбора сформулировать в виде набора некоторых правил или формул. Если возможна строгая формали- зация в виде задачи оптимизации, то от общей задачи принятия решений происходит переход к задаче 2-го класса. Здесь, однако, стоит отметить, что само по себе нахождение с по- мощью математических методов и компьютера оптимального Х* в си- стемном анализе не является окончанием процесса принятия решения. Окончательный выбор — принять или не принять к исполнению найден- ное Х* — выполняет человек (коллектив людей), обладающий специаль- ными полномочиями. Возможно, что предлагаемый результат покажется ему недостаточно подходящим, что приведет к новой формулировке усло-вий, нахождению второго варианта Х* уже для этих новых условий. Таким образом, очевидно, что многое зависит именно от тех людей (специали- стов, руководителей), которые готовят и осуществляют выбор и которые выступают участниками процесса принятия решений. 3 Задачи оптимизации. Линейные и нелинейные оптимизационные задачи. Нелинейные - https://studfile.net/preview/4521841/page:10/ Линейные - https://dspace.kpfu.ru/xmlui/bitstream/handle/net/32452/72-IEF_001181.pdf?sequence=1 4 Задача линейного программирования. Графическая интерпретация. Особенности постановки и поиска решения Обобщенная оптимизационная модель запишется следующим образом: y = f (X) → max (min), gj (X) ≤ (≥, =) bj, j = 1, 2, 3, ..., m, где y — выходная характеристика (критерий оптимизации), которую требуется привести к экстремальному значению — максимуму или минимуму в зависимости от ее смысла; f (X) — целевая функция, т. е. функция, указывающая зависимость критерия оптимизации от значения параметров Х; X = (x1, x2, x3, ..., xn) — набор из n параметров процесса, которыми можно управлять при поиске (создании) оптимального решения, эти параметры процесса называют в теории оптимизации переменными процесса, а Х — вектором состояния процесса; еще говорят, что х есть компоненты (координаты) вектора Х; gj (X) — функции-ограничения, число которых равно m; bj —некоторые постоянные величины, выражающие количественные значения ограничений, знаки (≥, =) подразумевают, что в записи ограничения вместо «≤» может быть или «≥», или «=». В зависимости от вида функций f (X), gj (X) различают такие известные модели, как модели задач линейного, нелинейного, целочисленного программирования и др. Модель задачи линейного программирования может использоваться для оптимального планирования выпуска продукции предприятия. Пусть предприятие может выпускать n видов продукции. Требуется определить, сколько единиц того или иного вида продукции следует произвести в заданный период, чтобы при этом получить максимальную прибыль и уложиться в имеющиеся ограничения на ресурсы (материальные, финансовые, кадровые и др.). Обозначим xi — число единиц продукции i-го вида; aji —затраты j-го ресурса на выпуск единицы i-й продукции; bj — имеющийся запас j-го ресурса; ci — прибыль от реализации единицы i-й продукции. При этих обозначениях можно записать следующую модель в виде классической задачи линейного программирования: 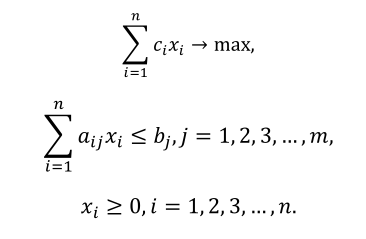 Решением данной задачи будет вектор X* = (x1*, x2*, x3*, ..., xn*), в кото- ром компоненты xi* (некоторые из них могут быть равны нулю) показыва- ют, сколько единиц i-й продукции нужно выпустить, чтобы прибыль при данных ресурсах была наибольшей 5 Задача нелинейного программирования. Графическая интерпретация. Особенности постановки и поиска решения. Особенности задач нелинейного программирования Нелинейное программирование занимается оптимизацией моделей задач, в которых либо ограничения qi(x) либо целевая функция Z(X) либо то и другое нелинейны. Найти max(min)=Z=z(X) в области где R – отношение порядка (=, ≥, ≤), Ω– область допустимых решений; bi– константа, i=1,m; X=(x1,…,xn)={xj}, j=1..n – план или вектор управления. Для выяснения трудностей решения задач данного класса, порождаемых нелинейностью, сопоставим задачи линейного и нелинейного программирования. Можно указать три характерные особенности для каждого класса. 6 Итерационные алгоритмы. Градиентный алгоритм. Поисковая оптимизация. 7 Многокритериальные задачи оптимизации. Основные подходы к их решению. Методы устранения многокритериальности. 8 Векторная оптимизация. Понятие эффективного решения. Оптимальность по Парето. 9 Задача выбора. Шкалы для оценки и сравнения альтернатив. В зависимости от того, какая информация об элементах ЗПР имеется и каким образом она задана, в каких условиях принимается и реализуется решение, определяют различные подходы и методы к принятию решений. Будем полагать, что: • множество альтернатив Х задается явно путем их перечисления, т. е. альтернативы уже известны; • для характеристики альтернатив можно ввести один или более показателей, отражающих различные свойства альтернатив, ко- торые представляют интерес с точки зрения ЛПР. Будем обозна- чать этот набор показателей как F = ( f1, f2, …, f i, …, f N), где N — чис- ло показателей; • значение каждого показателя f для каждой альтернативы х может быть выражено количественно и обозначено как f (x) (шкалы для оценки показателей будут рассмотрены ниже); • показатели в ЗПР являются сонаправленными. Это означает, что для всех показателей данной задачи соблюдается условие: чем больше f (x), тем полезнее для ЛПР альтернатива х; или же для всех — чем меньше f (x), тем полезнее для ЛПР альтернатива х. Показатель – характеристика свойства альтернативы Критерий – некоторое правило, условие выбора, которое отражает цель, интересы, предпочтения ЛПР. Например, как было показано выше: F (x) — показатель (точнее, оценка альтернативы х по этому показателю); F (х) → min — цель ЛПР, выраженная с помощью критерия минимизации. В зависимости от числа показателей ЗПР делятся на простые и слож- ные. К простым относятся те задачи, в которых для характеристики аль- тернатив используется один показатель F. В этом случае из множества Х, очевидно, выбирается та альтернатива х*, значение показателя которой является наибольшим (наименьшим) по сравнению с таковым у других альтернатив (как в приведенном выше примере с билетами). Когда по- казателей более одного, задача называется сложной. Если все показатели могут быть улучшены одновременно, то сложная задача вырождается в простую. Сложнее дело обстоит, когда показатели не улучшаются одновремен- но и, более того, улучшение одного может быть связано с ухудшением другого. Например, покупатель, как правило, желает одновременно ку- пить товар по наименьшей цене (чем меньше значение показателя цены, тем он лучше для покупателя) и с наибольшим качеством (чем выше зна- чение показателя качества, тем он лучше для покупателя). Практически оказывается, что улучшение товара по цене сопровождается ухудшением по качеству. В таких случаях говорят о задаче принятия решений в усло- виях многокритериальности. При этом подразумевается, что имеется не- сколько целей — и, следовательно, критериев, — каждая из которых со- стоит в улучшении «своего» показателя. В практических задачах выбора показатели могут измеряться не только разными единицами измерения, но и на разных шкалах. Шкалы измерений используются как для выражения значений кон- кретных показателей (критериев), так и для интегральной характеристи- ки альтернатив. В общем виде различают два основных типа шкал измерения — коли- чественные и качественные.  Если целью измерения является разделить альтернативы (или другие объекты) на классы по признакам типа «да — нет», «пригодный — непри- годный», «плохой — удовлетворительный — хороший» и т. п., используются так называемые номинальные, или классификационные шкалы. Отметим, что, несмотря на такую «словесную» формулировку классов, они могут быть пронумерованы. Например, шкале «плохой — удовлетворительный — хороший» можно сопоставить множество чисел {1, 2, 3} и считать, что оценка «хороших» альтернатив равна 3, а «плохих» — 1. Недостатком такой шкалы будет то, что она не предназначена для измерения расстояний между альтернативами, т. е. в случае с «плохими» и «хорошими» альтерна тивами нельзя сказать, насколько одни хуже или лучше других. При использовании ранговой шкалы альтернативы упорядочиваются по некоторому признаку. Номер альтернативы в упорядоченной последо- вательности называется ее рангом. Каждой альтернативе присваивается ранг. Обычно считается лучшей та альтернатива, ранг у которой мень- ше (это прямая ранговая шкала). Однако по договоренности можно усло- виться считать лучшей ту альтернативу, у которой ранг выше (обратная ранговая шкала). Как видно, ранг является некоторой интегральной харак- теристикой альтернативы. Вместо численной характеристики-ранга шкала может состоять из упорядоченных лингвистических значений, например «низкий — средний — высокий». Такая шкала называется порядковой. При оценке значений отдельных характеристик альтернатив, т. е. пока- зателей, чаще стараются использовать не качественные, а количественные шкалы. Наиболее обычной является абсолютная шкала. Здесь значение показателя выражается, как правило, в некоторых единицах измерения. Например, показатель временных затрат может принимать на этой шкале. значения 10, 100, 400 и т. д. и измеряться в часах, показатель стоимости — в рублях или другой валюте и т. п. Абсолютная шкала позволяет сравни- вать различные значения показателей между собой и определять расстоя- ния между ними. Определенным неудобством абсолютной шкалы является наличие единиц измерения. Покажем это на примере. Пусть предлагаются два ва- рианта выполнения мероприятия, т. е. две альтернативы Х1 и Х2, которые характеризуются двумя показателями: стоимости мероприятия f1 (едини ца измерения — рубли) и показателем временных затрат f2 (еди ница измерения — часы). Для первой альтернативы имеем оценки — f1 (Х1) = 1000 р., f2 (Х1) = 8 ч; для второй альтернативы — f1 (Х2) = 800 р., f2 (Х2) = 10 ч. Сравнить альтернативы по этим значениям и сказать, ка- кая лучше, мы не можем, не имея критерия выбора. Для сравнения аль- тернатив можно было бы использовать комплексный показатель F, такой, что F (X) = f1 (Х) + f2 (Х). Тогда можно было бы сказать, что лучше та альтернатива, у которой значение F меньше. Однако простое сложение «рублей с часами» будет, очевидно, неправильным. Для преодоления трудности необходимо избавиться от единиц измерения. Сделать это позволяет переход к шкале отношений. На шкале отношений (относительной шкале) значения показателей измеряются в относительных (безразмерных) единицах и характеризуют их сравнительные оценки. Для перехода от абсолютной к относительной шкале применяется нормирование показателей. Распространенным спо- собом является соотнесение измеренного значения показателя f с неко- торым эталонным, нормативным или другим специальным значением fe. Если сравнивается множество альтернатив, в качестве fe может выступать значение показателя той альтернативы, для которой он принимает самое большое (самое маленькое) значение по сравнению с другими на абсолют- ной шкале. Продолжая последний пример, положим, что есть некоторая альтернатива Хe, которую можно считать эталоном «плохих альтернатив», и известно, что f1 (Хe) = 2000 р., f2 (Хe) = 40 ч. Тогда переход к оценкам показателей на относительной шкале можно выполнить по следующим формулам нормирования: f1 (Х1)н = f1 (Х1) / f1 (Хe) = 1000 р. / 2000 р. = 0,5; f2 (Х1)н = f2 (Х1) / f2 (Хe) = 8 ч / 40 ч = 0,2, где f2(Х1)н — нормированное значение показателя. 96Для второй альтернативы имеем: f1 (Х2)н = f1 (Х2) / f1 (Хe) = 800 р. / 2000 р. = 0,4; f2 (Х2)н = f2 (Х2) / f2 (Хe) = 10 ч / 40 ч = 0,25. Теперь, имея безразмерные величины, вычислим комплексный пока- затель F для обеих альтернатив. Вычислять будем как среднее арифмети- ческое значение двух частных нормированных показателей: F (Х1) = 0,5 ( f1 (Х1)н + f2 (Х1)н) = 0,5 (0,5 + 0,2) = 0,35; F (Х2) = 0,5 ( f1 (Х2)н + f2 (Х2)н) = 0,5 (0,4 + 0,25) = 0,325. Если положить, что критерием выбора является критерий миними- зации затрат, т. е. F (Х) → min, то лучшей будет альтернатива Х2. Интервальная шкала, как и абсолютная или относительная, обладает также характеристикой расстояния между отдельными градациями шка- лы. Это расстояние между отдельными градациями задается некоторым интервалом. Обычно принимается, что интервал как единица измерения на шкале остается неизменным. Шкальные значения можно складывать. Например, измерять экономичность модели какого-то технического объекта можно по шкале, имеющей градации [27]: • чрезвычайно экономичен; • очень экономичен; • в известной мере экономичен; • в известной мере неэкономичен; • очень неэкономичен; • чрезвычайно неэкономичен. Межу этими градациями условно задано расстояние — один интер- вал (или другое количество равных интервалов). Поэтому можно не толь- ко дать характеристику объекта на данной шкале, но и сказать, насколько он далеко от другого объекта (на каком числе интервалов). Таким образом, интервальная шкала не только содержит всю инфор- мацию, заложенную в порядковой, но также позволяет найти различия между объектами. Общеизвестным примером из повседневной жизни служит шкала температуры [27]. Мы знаем, что температура может измеряться в разных интервалах и с разными точками отсчета. Существуют преобразования перехода от одной шкалы температуры к другой эквивалентной шкале. Так, переход от шкалы Цельсия к шкале Фаренгейта задается линейным преобразованием шкальных значений [4, 27]: to F = 1,8 to C + 32. Применение интервальной шкалы позволяет использовать еще один способ нормирования показателей — относительно границ заданного ин- тервала: f н = ( f – fmin) / ( fmax – fmin), где fmax, fmin — границы некоторого интервала, например, наибольшее и наименьшее значения показателя для некоторого множества объектов. При оценке и сравнении альтернатив с помощью экспертов широкое распространение находит балльная шкала. На этой шкале показателям или всей альтернативе присваиваются некоторые баллы — оценки, которые выставляют эксперты. Например, эксперт может характеризовать альтернативу «план реорганизации предприятия» с точки зрения (по показателю) его реальной выполнимости. Для этого можно использовать 10-балльную шкалу, где 10 баллов будут означать наилучшую, а 1 — наихудшую оценку, которая соответствует мнению эксперта о том, что план является невыполнимым. Считается, что балльная шкала занимает промежуточное положение между качественными и количественными шкалами. Чем меньше града- ций у балльной шкалы и чем проще правила начисления баллов, тем бли- же такие шкалы к качественным, ранговым. Наоборот, чем число градаций больше и сложнее правила начисления баллов, тем балльная шкала бли- же по своим свойствам и возможностям к количественной, интервальной. 10 Методы выбора в условиях многокритериальности. Модели сверки критериев. Коэффициенты относительной важности. 11 Выбор на основе сравнения с эталоном и метрики расстояний. 12 Метод попарных сравнений. 13 Case Based Reasoning (CBR) - вывод решения на основе прецедентов 14 . Принцип гарантийного результата. 15 Методы экспертных оценок в процессах информационной подготовки принятия решений. Процедура экспертного оценивания. 16 Экспертное оценивание. Экспертная классификация. Экспертное ранжирование. Задача формирование исходного множества объектов. Задача принятия решений (ЗПР) направлена на определение наилучшего (оптимального) способа действий для достижения поставленных целей. Под целью понимается идеальное представление желаемого состояния или результата деятельности. Если фактическое состояние не соответствует желаемому, то имеет место проблема. Выработка плана действий по устранению проблемы составляет сущность задачи принятия решений. Проблема всегда связана с определенными условиями, которые обобщенно называют ситуацией. Совокупность проблемы и ситуации образует проблемную ситуацию. Выявление и описание проблемной ситуации дает исходную информацию для постановки задачи принятия решений. Субъектом всякого решения является лицо, принимающее решение (ЛПР). Понятие ЛПР является собирательным. Это может быть одно лицо – индивидуальное ЛПР или группа лиц, вырабатывающих коллективное решение, групповое ЛПР. Для помощи ЛПР в сборе и анализе информации и формировании решений привлекаются эксперты – специалисты по решаемой проблеме. Понятие эксперта в теории принятия решений трактуется в широком смысле и включает сотрудников аппарата управления, подготавливающих решение, ученых и практиков. Принятие решений происходит во времени, поэтому вводится понятие процесса принятия решений. Этот процесс состоит из последовательности этапов и процедур и направлен на устранение проблемной ситуации. В процессе принятия решений формируются альтернативные (взаимоисключающие) варианты решений и оценивается их предпочтительность. Предпочтение – это интегральная оценка качества решений, основанная на объективном анализе (знании, опыте, проведении экспериментов и расчетов) и субъективном понимании ценности, эффективности решений. Для осуществления выбора наилучшего решения индивидуальное ЛПР определяет критерий выбора. Групповое ЛПР производит выбор на основе принципа согласования Конечным результатом ЗПР является решение, которое представляет собой предписание к действию. С содержательной точки зрения решением может быть способ действия, план работы, вариант проекта и т.п. Решение является одним из видов мыслительной деятельности и проявлением воли человека и имеет свои характерные признаки, рассмотренные ранее. Решение называется допустимым, если оно удовлетворяет ограничениям: ресурсным, правовым, морально-этическим. Решение называется оптимальным (наилучшим), если оно обеспечивает экстремум (максимум или минимум) критерия выбора при индивидуальном ЛПР или удовлетворяет принципу согласования при групповом ЛПР. Обобщенной характеристикой решения является его эффективность. Эта характеристика включает эффект решения, определяющий степень достижения целей, и стоимость решения – совокупность затрат ресурсов для принятия и реализации решения. Таким образом, эффективность решения - это степень достижения целей, отнесенная к затратам на их достижение. Решение тем эффективнее, чем больше степень достижения целей и меньше стоимость затрат |
