Контрольный тест по алгебре для 10 кл. Контрольный тест по алгебре для 10 го класса
 Скачать 21.75 Kb. Скачать 21.75 Kb.
|
|
Контрольный тест по алгебре для 10 –го класса (20 вопросов с пятью вариантами ответов из которых один правильный). 1. Найдите значение выражения: 0,54 + 2· ( 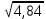 )2 = )2 =А) 9,84; Б) 8,35; В) 9,99; С) 10,22; Д) 11,8. 2. Извлеките квадратный корень: 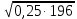 = =А) 7; Б)10; В) 0,5; С) 14; Д) – 7. 3. Освободитесь от иррациональности в знаменателе дроби: 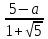 = =А) 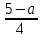 ; Б) ; Б) 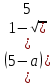 ; В) ; В) 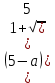 ; С) ; С) 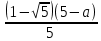 ; Д) ; Д) 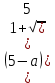 . .4. Решить квадратное уравнение: х2 – 8х – 9 =0. А) {1;9 }; Б) {- 9; 1 }; В) {-1;9 }; С) {2; 8}; Д) {- 2 ;8 }; 5.Найти корень уравнения: - у·(у+7) = (2+у)(у – 2). А) {- 4; 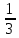 }; }; Б) {0,5; 4 }; В) {- 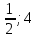 }; }; С) {4; 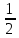 }; }; Д) {- 4; 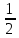 }; };6. Найдите корни дробно-рационального уравнения: 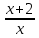 - - 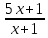 = 0 = 0А) {1\2; 1 }; Б) {-1\2; 1 }; В) {-1;1\2 }; С) {-0,5; - 1 }; Д) {-1; 2 }; 7. Решить уравнение способом введения новой переменной: х4 – 5х2 +4=0 А) (-1;1); (-2; 2); Б) (-1;2); (-2;1); В) (1;1);(- 2;2); С) (- 1;1), (- 2; -3); Д) (2;-3), (1;- 1). 8. Найдите ординату точки графика функции у=- 2х2 +3х – 5, абссица которой равна - 4: А) 49; Б) -50; В) – 49; С) 50; Д) 39. 9. Постройте график функции . Найдите вершину и ось симметрии , опишите свойства функции у= (х+2)2 – 6. А) х=0,(2;0); Б) х=2, (0;2); В) х=2; (2 ,0); С) х=0,(1;0); Д) х=2,(-2;0). 10. Решите квадратное неравенство: х2 –х- 56 > 0 А) (- 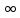 ; + ; + 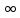 ); ); Б) (- 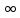 ; 7) ; 7)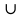 (8; + (8; +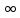 ), ), В) (- 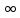 ; 8) ; 8) (9; + (9; + ), ), С  ) (- ) (-  ; -7) ; -7)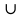 (8; + (8; +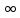 ), ), Д) (- 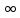 ; -9) ; -9)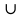 (7; + (7; +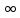 ), ), 11. Решите систему неравенств: Х2 - 4 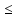 0 0Зх - 2 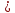 0 0А) 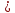 , , Б) (-2; 2\3) , В) [-2; 2\3], С) [-3;2), Д) [-2; 2\3). 12. Корням уравнения arcsin( x2 – 3) = 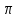 \2 являются числа: \2 являются числа:А) 2; Б) – 2; В) -2; 2, С) 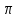 , , Д) - 2; - 2. 13. Решить уравнение вида arcs in (x2 -2x -7) = arcsin(x -3) А) 4; Б) – 4; В) 5; С) – 5; Д) 4,5. 14. Корнями уравнения sin5xcos3x – cos5xsin3x = - 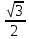 являются: являются:А) (-1)к · 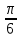 + + 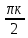 , к є Z. ; , к є Z. ; Б) (-1)к+1 · 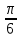 + + 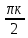 , к є Z., , к є Z., В) 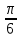   +2 +2 к , к є Z. к , к є Z.С)  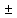 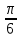 + 0,5 + 0,5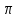 к , к є Z., к , к є Z., Д) (-1)к · 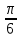 - - 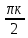 , к є Z. , к є Z.15. Вычислить : 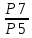 = =А) 42; Б) – 42; В) 44, С) 40, Д) 41. 16. Выполните деление «уголком» многочлена: Х3 – 2х2- 3х- 5 на многочлен х2- 3х – 1. А) х-1, остаток х+4; Б) х+1, ост. Х-4, В) х+1, ост. Х-2; С) х-1, ост. Х+2; Д) х+1, остаток х+4. 17. Найдите предел последовательности: 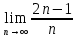 А) 2; Б) – 2; В) 1; С) -1; Д) 3. 18. Найдите асимптоты графика функции у= f(x): f(x) = 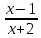 , ,А) верхняя асимптота х= -2, горизонтальная - у= 1; Б) верхняя асимптота х= 2, горизонтальная - у= - 1; В) верхняя асимптота х= -1, горизонтальная - у= 2; С) верхняя асимптота х= 1, горизонтальная - у= - 2; Д) верхняя асимптота х= -2, горизонтальная - у= -1; 19. Пользуясь правилами вычисления производных, найдите f(x)' f(x)= x2 + 3x - 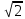 ; ;А) 2х+3; Б) 3х+2; В) - 2х-3; С) - 2х + 3; Д) 3х -2. 20. Найдите значение производной функции f(x) в точке х0 : f(x) =х(х-3); х0 = 4. А) - 5; Б) 5; В) – 4; С) 4; Д) 3. |
