тест. Координатный метод на плоскости
 Скачать 16.99 Kb. Скачать 16.99 Kb.
|
|
ТЕСТ по теме «Координатный метод на плоскости» 1. По координатам точек А (10; 5) и В (– 9; 9) определите каковы эти векторы 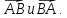 Выберите правильный ответ Выберите правильный ответа) не коллинеарны; б) равные; в) сонаправленные; г) равной длины. Ответ: равной длины. 2. По координатам векторов 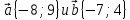 определите координаты вектора определите координаты вектора 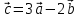 а) (10;25); б) (– 10; 25); в) (10; – 25); г) (– 10; – 25). Ответ: (– 10; 25). 3. Найдите числа x и y, удовлетворяющие условию – 15 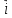 +y +y 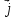 =x =x 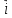 +11 +11 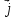 а) x=11; y=15; б) x= – 15; y= – 11; в) x=15; y=11; г) x= – 15; y=11. Ответ: x= – 15; y=11. 4. Дан вектор 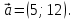 Вычислите Вычислите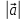 а) 13; б) 10; в) – 13; г) 12. Ответ:13. 5. Расстояние между точками А и В с координатами А (7; 2) и В (3; 5) равно а) – 5; б) 25; в) 17; г) 5. Ответ: 5. 6. Даны координаты вектора и конечной точки этого вектора. Определите координаты начальной точки вектора 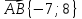 , В(– 1; 8) , В(– 1; 8) а) A (0; –6); б) A (–6; 0); в) A (6; 0); г) A (–6; –6); Ответ: A (–6; 0). 7. Среди векторов 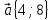 ; ; 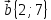 ; ; 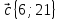 ; ; 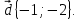 Укажите пару противоположно направленных Укажите пару противоположно направленных а) векторы b и c; б) векторы a и d; в) векторы a и c; г) векторы b и d. Ответ: векторы a и d. 8. Напишите уравнение прямой ax+by+c=0, все точки которой находятся в равных расстояниях от точек А (1; 1) и В (6; 11) а) 2x–y–12=0; б) 2x+y–13=0; в) –2x+y+13=0; г)2x+y+13=0. Ответ: 2x+y–13=0. 9. Формула окружности 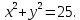 Определите место точки В (–1; –2) Определите место точки В (–1; –2)а) вне круга; б) внутри круга; в) на окружности. Ответ: внутри круга. 10. Уравнение прямой имеет вид –6x+24y+48=0. Найдите координаты точки, в которой она пересекает ось абсцисс а) (–8; 0); б) (2; 0); в) (0; 8); г) (8; 0). Ответ: (8; 0). 11. Некоторой прямой принадлежат точки А (–1; 2) и С (0; 1). Уравнение прямой имеет вид а) x+y+1=0; б) –x–y+1=0; в) x–y+1=0; г) –x–y–1=0. Ответ: x–y+1=0; 12. Используя данную формулу окружности 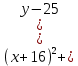 определите координаты центра О окружности определите координаты центра О окружности а) (–16;25); б) (4; –5); в) (16; –25); г) (–4; 5). Ответ: (–16; 25). 13. Даны точки А (8; 6) и В (6; 2). Найдите координаты точки С, если известно, что В – середина отрезка АС, а точка D – середина ВС а) C (–2; 4) и D (2; 1); б) C (–2; 4) и D (4; –2); в) C (–2; – 4) и D (2; – 1); г) C (4; –2) и D (5; 0). Ответ: C (4; –2) и D (5; 0). 14. Четырехугольник ABCD имеет вершины с координатами A(13; 3); B(15;6); C(12; 8) и D(10; 5) является прямоугольником, если…. а) AB=BD; б) AC=BD; в) AB=AD; г) AB=CD. Ответ: AC=BD. 15. Прямоугольник ABCD имеет вершины с координатами A (13; 3); B (15;6); C (12; 8) и D (10; 5). Найдите его площадь а) 8; б) 13; в) 26; г) 16. Ответ:13. 16. Найдите площадь данного треугольника, зная координаты его вершин K (0; 6); P (4; –2); H (2; 18). а) 64; б) 32; в) 16; г) 28. Ответ: 32. 17. Используя данную формулу окружности 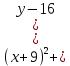 . Найдите величину радиуса R . Найдите величину радиуса R а) 3; б) 4; в) 5; г) 12. Ответ:12. 18. Найдите косинус угла А треугольника АВС, если его вершины имеют координаты А(1; 1); В(4; 1); С(4;5) а) cosA=0; б) cosA=0,6; в) cosA=0,8; г) cosA= – 0,6. Ответ: cosA=0,6. 19. Вершины треугольника имеют координаты А (1; 3); В (2; 1) и С (3;4). Найдите координаты точки М пересечение медиан. а) M (8/3; 2); б) M (2; 8/3); в) M (–2; – 8/3); г) M (2; –8/3). Ответ: M (2; 8/3). 20. Определите вид треугольника, если его вершины имеют координаты А (0;1); В (1; -4); С (5; 2). а) равносторонний; б) равнобедренный; в) разносторонний. Ответ: равнобедренный. |
