Практика. Практика 3,4. Корреляционно регрессионный анализ
 Скачать 1.42 Mb. Скачать 1.42 Mb.
|
|
Корреляционно - регрессионный анализ Корреляционный анализ позволяет сделать вывод о силе взаимосвязи между парами данных х и у, а регрессионный анализ используется для прогнозирования одной переменной (у) на основании другой (х). Иными словами, в этом случае пытаются выявить причинно-следственную связь между анализируемыми совокупностями. 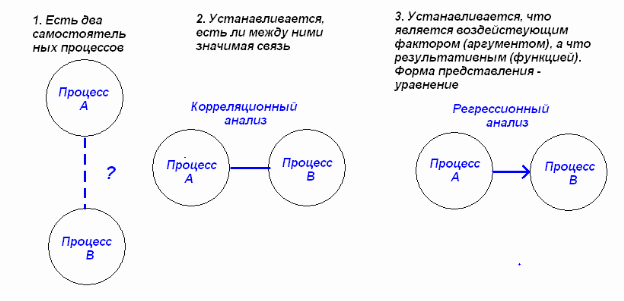 Принято различать два вида связи между числовыми совокупностями – это может быть функциональная зависимость или же статистическая (случайная). При наличии функциональной связи каждому значению воздействующего фактора (аргумента) соответствует строго определенная величина другого показателя (функции), т.е. изменение результативного признака всецело обусловлено действием факторного признака.  Для количественной оценки существования связи между изучаемыми совокупностями случайных величин используется специальный статистический показатель – коэффициент корреляции r. Если предполагается, что эту связь можно описать линейным уравнением типа y = a + bx (где a и b − константы), то принято говорить о существовании линейной корреляции. Коэффициент r − это безразмерная величина, она может меняться от 0 до ±1. Чем ближе значение коэффициента к единице (неважно, с каким знаком), тем с большей уверенностью можно утверждать, что между двумя рассматриваемыми совокупностями переменных существует линейная связь. Иными словами, значение какой-то одной из этих случайных величин (y) существенным образом зависит от того, какое значение принимает другая (x). Если окажется, что r = 1 (или −1), то имеет место классический случай чисто функциональной зависимости (т.е. реализуется идеальная взаимосвязь). Корреляцию и регрессию принято рассматривать как совокупный процесс статистического исследования, поэтому их использование в статистике часто именуют корреляционно-регрессионным анализом. Если между парами совокупностей просматривается вполне очевидная связь (ранее было исследовано), то, можно сразу приступать к поиску уравнения регрессии. Если же исследования касаются какого-то нового процесса, ранее не изучавшегося, то наличие связи между совокупностями является предметом специального поиска. При этом условно можно выделить методы, которые позволяют оценить наличие связи качественно, и методы, дающие количественные оценки. Чтобы выявить наличие качественной корреляционной связи между двумя исследуемыми числовыми наборами экспериментальных данных, существуют различные методы, которые принято называть элементарными, которые включают в себя следующие операции: − параллельное сопоставление рядов; − построение корреляционной и групповой таблиц; − графическое изображение с помощью поля корреляции. Другой метод, более сложный и статистически надежный, — это количественная оценка связи посредством расчета коэффициента корреляции и его статистической проверки. Существуют различные аналитические приемы определения коэффициента r. При использовании данной формулы отпадает необходимость вычислять отклонения текущих (индивидуальных) значений от средней величины. Это исключает ошибку в расчетах при округлении средних величин.  Зная коэффициент корреляции, можно дать качественно-количественную оценку тесноты связи. Используются, например, специальные табличные соотношения (так называемая шкала Чеддока).  Далее необходимо проверить корреляционную зависимость на влияние «третьего фактора» при помощи расчета коэффициента детерминации R2, который равен квадрату коэффициента корреляции (r2). Он показывает, в какой мере изменчивость у (результативного признака) объясняется поведением х (факторного признака), т.е. какая часть общей изменчивости у вызвана собственно влиянием х. Этот показатель вычисляется путём простого возведения в квадрат коэффициента корреляции. Тем самым доля изменчивости у, определяемая выражением 1− R2, оказывается необъясненной. Допустим к примеру, что коэффициент корреляции совокупности данных, относящихся к производственным затратам, равняется 0,86. Следовательно, значение R2 равно R2 = 0,862 = 0,74 или 74 %. Это значение R2 говорит о том, что 74 % вариации (изменчивости), скажем, недельных затрат объясняется количеством изделий, выпущенных за неделю. Остальная часть (26 %) вариации общих затрат объясняется какими-то другими причинами. Это значит, что более чем на 74 % мы знаем, что влияет на изменение изучаемого параметра, но почти на 26 % ничего не знаем о причинах наблюдаемой изменчивости. Величина этого коэффициента меняется в пределах от 0 до 1. Чем ближе он к единице, тем, следовательно, меньше в нашей модели процесса влияние неучтенных факторов и тем больше оснований считать, что указанная зависимость отражает степень эффективности воздействия изучаемого фактора. Далее следует выявить связь, описанную не только формулой, но и математически, Исследование такой ситуации и является задачей регрессионного анализа, который дает предсказание (прогнозирование) одной переменной на основании другой. Регрессионный анализ четко распределяет роли между изучаемыми характеристиками − одна из них является аргументом, а вторая функцией. Переменная, которая прогнозируется (функция), обозначается как у, а переменная, которая используется для такого прогнозирования (аргумент или фактор), − это х. Целью регрессионного анализа является поиск ответа на вопрос: «Каков вид этой связи? Что на что влияет?» При изучении связи показателей коммерческой деятельности применяются различного вида уравнения прямолинейной и криволинейной связи. Формально могут возникать ситуации двух типов: 1. Вид функциональной зависимости неизвестен. В этом случае нужно решить предварительно задачу, направленную на отыскание подходящей функциональной зависимости. 2. Вид функциональной зависимости известен и требуется только найти ее параметры (коэффициенты регрессии b0, b1, b2, …). Термином линейный регрессионный анализ обозначают такое прогнозирование, которое описывается линейной взаимосвязью между исследуемыми переменными: y = b0 + b1x. В случае криволинейных зависимостей применяются математические функции следующего вида: гиперболическая y = b0 + b1 /x; показательная y = b0 + b1x; степенная y = b0xb1; параболическая y = b0 + b1x + b2x2; логарифмическая y = b0 + b1lgx; экспоненциальная y = b0exp (b1x) и другие. Решение математических уравнений связи предполагает вычисление по исходным данным их параметров (свободного члена b0 и коэффициентов регрессии b1, b2, …). При всем разнообразии эмпирических формул все же имеется вид аналитической зависимости, получивший широкое распространение. Им является уравнение регрессии в виде многочленов, расположенных по восходящим степеням изучаемого фактора и одновременно линейных ко всем коэффициентам. Такая формула имеет вид: y = f(x) = b0 + b1x + b2x2 +…+ bm xm, где b0 , b1 , b2,…, bm − коэффициенты, подлежащие определению. Этот ряд − сходящийся, т.к. стремится к некоторому пределу.__ Для определения коэффициентов уравнения регрессии b применяют разные методы (графический, метод средних), однако наибольшее распространение получил метод наименьших квадратов. Все процессы, которые имеют заведомо плавное течение, принято изображать также плавными кривыми, так, чтобы кривая проходила по возможности ближе ко всем точкам на графике. Основное положение МНК: сумма квадратов отклонений εi экспериментальных точек от кривой по вертикальному направлению, т.е. сумма квадратов величин εi, должна быть наименьшей (Σ εi2 = минимум). Или − сумма квадратов отклонений известных (экспериментальных) значений исследуемой функции и соответствующих значений аппроксимирующей функции (теоретическими показателями) должна быть наименьшей. Довольно часто при описании аппроксимирующей функции ограничиваются простым видом полиноминальной зависимости, полагая ее линейной, т.е. в виде уравнения прямой y = b0 + b1x. Здесь свободный член b0 характеризует сдвиг и равен тому значению у, которое получается при х = 0, а коэффициент b1 определяет наклон линии. Отыскание коэффициентов b0 и b1 осуществляется по МНК. Пусть имеется n экспериментальных точек (n пар наблюдений): (x1,y1); (x2, y2);… ( xn, yn). Введем следующие обозначения: уi – это измеренные (экспериментальные) значения изучаемого параметра, а ŷi – его теоретические (рассчитанные по уравнению) показатели. Предположим, что экспериментальные точки на графике укладываются так, что по ним вполне возможно провести прямую линию. Значения функции ŷi в этом случае можно записать в виде линейного уравнения: ŷi = b0 + b1 xi . Расстояние по ординате (вертикали) от точки yi до прямой составит: b0 + b1 xi − yi = εi, где b0 + b1 xi = ŷi − рассчитанное (теоретическое) значение функции; yi − ее измеренное значение и εi − разница (расстояние) между ŷi и yi. В соответствии с МНК полагаем, что искомая прямая будет наилучшей, если сумма квадратов всех расстояний (b0 + b1 xi − yi)2 = εi2 окажется наименьшей. Минимум этой суммы ищется по правилам дифференциального исчисления. В результате для определения b0 и b1 используются следующие уравнения:  Особенности МНК: Этот метод не дает ответа на вопрос о том, какого вида функция лучше всего аппроксимирует конкретные экспериментальные точки. Вид интересующей нас функции должен быть задан на основе каких-то физических или экономических соображений. МНК позволяет лишь выбрать, какая из прямых (парабол, экспонент) является лучшей прямой (параболой, экспонентой) для прогнозирования. МНК является достаточно точным приемом и позволяет получить вполне надежные результаты. Одновременно он является интерполяционным методом, поскольку обеспечивает с определенной вероятностью предсказание любых значений yi в интервале изученных значений xi. Множественная регрессия Так как в большинстве случаев приходится иметь дело с экспериментальными данными, касающимися влияния более чем одного фактора. Прогнозирование единственной переменной у на основании нескольких переменных хk называется множественной регрессией. В этом случае математическая модель процесса представляется в виде уравнения регрессии с несколькими переменными величинами, т.е. у = f (b0, …, xk). Общий вид уравнения множественной регрессии обычно стараются представить в форме линейной зависимости: у = b0 + b1x1 + b2x2 + …+ bkxk, где b0 – свободный член (или сдвиг); b1, b2 , …, bk − коэффициенты регрессии, которые подлежат вычислению методом наименьших квадратов. При анализе уравнения множественной регрессии (как и в случае простой регрессии) используется также такое понятие, как ошибка прогнозирования Δу. Последняя понимается как разность между рассчитанным (теоретическим) значением функции ŷi и ее измеренным (опытным) значением yi, т.е. Δу = ŷi − yi. Статистический вывод о значимости уравнения обычно проверяется в следующей последовательности. 1. Сначала проводится общая проверка методом F-теста, целью которой является выяснение, объясняют ли х-переменные значимую долю вариации у, т.е. превалирует ли влияние факторов хk на изменение функции у над ее колебаниями случайного порядка; если регрессия не является значимой, то говорить больше не о чем. 2. Если регрессия оказывается значимой, то можно продолжить анализ, используя t-тесты для отдельных коэффициентов регрессии; в этом случае необходимо выяснить, насколько значимой является влияние той или иной переменной х на параметр у при условии, что все другие факторы хk остаются неизменными. Построение доверительных интервалов и проверка гипотез на адекватность для отдельного коэффициента регрессии основывается на определении стандартной ошибки. Каждый коэффициент регрессии имеет свою стандартную ошибку Sb1, Sb2,…, Sbk. Пример: Провести корреляционно-регрессионный анализ факторов, влияющих на образование дефектов при производстве и провести проверку R2, F-тест при α =0,05. Исходные данные
В результате проведения корреляционного анализа было выявлено два фактора х2 и х3 имеющие высокую корреляционную связь с исследуемым параметром. Далее найдем уравнение множественной корреляции. Расчеты приведены в Excel Уравнение регрессии y= 12,32 + 0,123х1 + 5,142х2 Качество построенной модели в целом можно оценить при помощи коэффициента множественной детерминации R2 = 0,78 – соответственно факторами, представленными в модели, можно описать 78% вариации исследуемого признака (y). Стандартная ошибка 9,81, что меньше 10%. Значимость уравнения множественной регрессии в целом оценивается с помощью F -критерия Фишера = 30,9 Фактическое значение F –критерия Фишера сравнивается с табличным при уровне значимости α и числе степеней свободы: k1 = 2 (число воздействующих факторов), k2 = n-m-1, где n – число наблюдений, m – число факторов. Если выполняется неравенство Fрасч < Fтабл, то с уверенностью, на 95 %, можно утверждать, что рассматриваемая зависимость у = b0 + b1x1 + b2x2 +…+ bkxk является статистически значимой. В противном случае наоборот. Для анализа уравнения будем пользоваться величиной Fрасч, обратной представленной Excel. Она составит 1:30,9 = 0,03, соответственно 0,03 < 3,59 - уверенно можно говорить о высокой степени адекватности анализируемого уравнения. Значимость F - 2,16E-06, т.е. это говорит о том, что действительно обнаруживается устойчивая зависимость рассматриваемой функции у. Коэффициент детерминации R2расч составляет 0,78. Таблица для тестирования на уровне значимости 5 % в случае выборки n = 20 и числа переменных k = 2 дает критическое значение R2крит = 0,297 (прил.2). Поскольку выполняется соотношение R2расч > R2крит, то с вероятностью 95% можно утверждать о наличии значимости данного уравнения регрессии. Таким образом, существует взаимосвязь между параметром у и переменными хk. Однако нам пока неясно, каково влияние конкретных факторов х1 и х2 на исследуемую функцию у: действуют ли оба фактора или только какой-то один из них. Поэтому предстоит определить значимость отдельных коэффициентов регрессии b1 и b2. Для этой цели используется так называемый t-тест. Анализируемый коэффициент считается значимым, если его t-критерий по абсолютной величине превышает 2,093, что соответствует уровню значимости 0,05 (приложение 3). В нашем случае t1 = 6.09, t2 = 0.17, соответственно значимым фактором будет только один фактор x1 – численность работников. Соответственно, можно отметить неслучайный характер влияния только для «Объем выпуска продукции». Для построения адекватной модели множественной регрессии необходимо заменить переменную «Время такта» на более значимую. Приложение 1  Приложение 2  Приложение 3 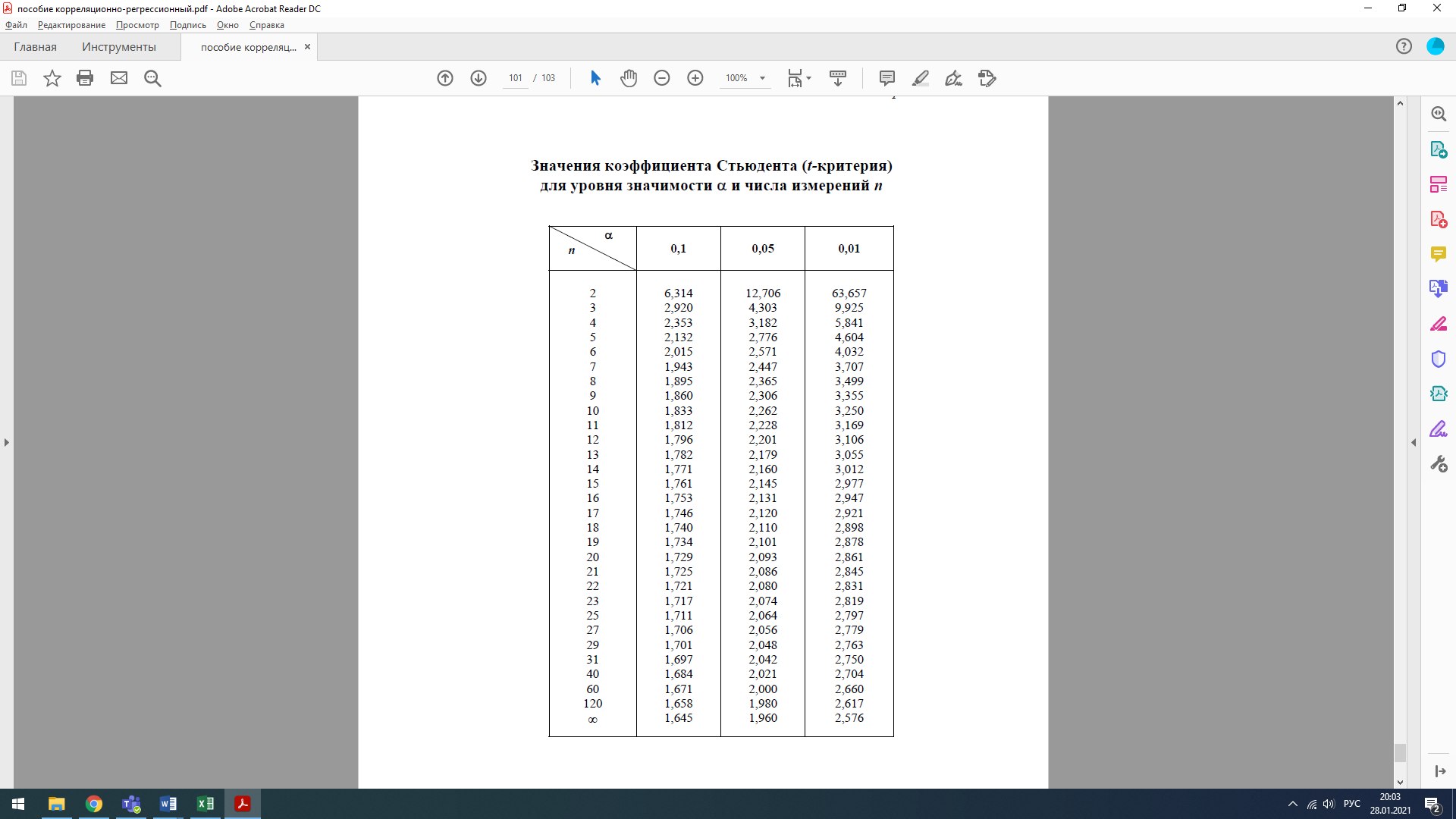 Число измерений = выборке, т.е. 20, соответственно е-критерий Стьюдента равен 2,093, минимальное значение t-критерия Стьюдента 1,96 Задание: Провести корреляционно-регрессионный анализ влияния факторов на количество несоответствий продукции, провести проверку R2, F-тест, t-тест при α =0,05. Исходные данные
|
