Задача сведения минимума. Кратчайшие пути в графах

• Название: Кратчайшие пути в графах
• Анкор: Задача сведения минимума
• Дата: 20.09.2022
• Размер: 223.52 Kb.
• Имя файла: Kursach_Pechat(1).docx
• Тип: Документы; #686147

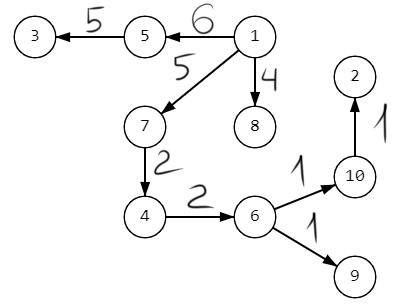
Часть 3. Кратчайшие пути в графах

Задание 1. Определить кратчайшие пути от вершины 1 до всех остальных вершин графа, используя алгоритм Дейкстры. Построить дерево кратчайших путей. Отрицательные длины в матрице заменить положительными.

Задание 2. Определить кратчайшие пути от вершины 1 до всех остальных вершин графа, пользуясь алгоритмом Беллмана. Построить дерево кратчайших путей.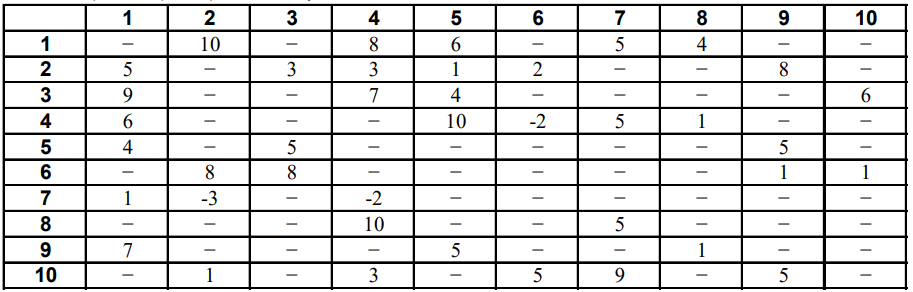

Алгоритм Дейкстры

	1	2	3	4	5	6	7	8	9	10
1	0+	∞	∞	∞	∞	∞	∞	∞	∞	∞	𝑝 = 1
2	0+	10	∞	8	6	∞	5	4+	∞	∞	𝑝 = 8
3	0+	10	∞	8	6	∞	5+	4+	∞	∞	𝑝 = 7
4	0+	8+	∞	7	6+	∞	5+	4+	∞	∞	𝑝 = 5
5	0+	8+	11	7	6+	∞	5+	4+	11	∞	𝑝 = 2
6	0+	8+	11	7+	6+	10	5+	4+	11	∞	𝑝 = 4
7	0+	8+	11	7+	6+	9+	5+	4+	11	∞	𝑝 = 6
8	0+	8+	11	7+	6+	9+	5+	4+	10	10+	𝑝 = 10
9	0+	8+	11	7+	6+	9+	5+	4+	10+	10+	𝑝 = 9
10	0+	8+	11+	7+	6+	9+	5+	4+	10+	10+	𝑝 = 3

1. 
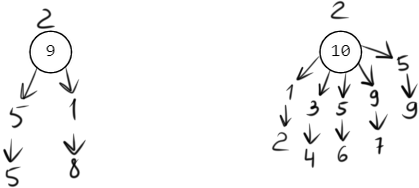
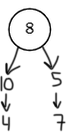
   Заполняем вторую строку таблицы
   

𝑑⁽2⁾ = min⁽∞; 0 + 10⁾ = 10

𝑑⁽4⁾ = min⁽∞; 0 + 8⁾ = 8

𝑑⁽5⁾ = min⁽∞; 0 + 6⁾ = 6

𝑑⁽7⁾ = min⁽∞; 0 + 5⁾ = 5

𝑑⁽8⁾ = min⁽∞; 0 + 4⁾ = 4

𝑝 = 8

2. 
   Заполняем третью строку таблицы
   

𝑑⁽4⁾ = min⁽8; 4 + 10⁾ = 8

𝑑⁽7⁾ = min⁽5; 4 + 5⁾ = 5

𝑝 = 7

3. 
   Заполняем четвёртую строку таблицы
   

𝑑⁽2⁾ = min⁽10; 5 + 3⁾ = 8

𝑑⁽4⁾ = min⁽8; 5 + 2⁾ = 7

𝑝 = 5

4. 
   Заполняем пятую строку таблицы
   

𝑑⁽3⁾ = min⁽∞; 6 + 5⁾ = 11

𝑑(9) = min(∞; 6 + 5) = 11

𝑝 = 2

5. 
   Заполняем шестую строку таблицы
   

𝑑(3) = min(11; 8 + 3) = 11

𝑑(4) = min(7; 8 + 3) = 7

𝑑(6) = min(∞; 8 + 2) = 10

𝑑(9) = min(11; 8 + 8) = 11

𝑝 = 4

6. 
   Заполняем седьмую строку таблицы
   

𝑑(6) = min(∞; 7 + 2) = 9

𝑝 = 6

7. 
   Заполняем восьмую строку таблицы
   

𝑑⁽3⁾ = min⁽11; 9 + 8⁾ = 11

𝑑⁽9⁾ = min⁽11; 9 + 1⁾ = 10

𝑑⁽10⁾ = min⁽∞; 9 + 1⁾ = 10

𝑝 = 10

8. 
   Заполняем девятую строку таблицы
   

𝑑⁽9⁾ = min⁽10; 10 + 5⁾ = 10

𝑝 = 9

9. 
   Остаётся p = 3.
   

Дерево кратчайших путей:

Алгоритм Беллмана

	1	2	3	4	5	6	7	8	9	10
1	0	10	∞	8	6	∞	5	4	∞	∞
2	0	2	11	3	6	6	5	4	11	∞
3	0	2	5	3	6	1	5	4	10	17
4	0	2	5	3	6	1	5	4	2	2
5	0	2	5	3	6	1	5	3	2	2
6	0	2	5	3	6	1	5	3	2	2

Из вершины 1 выходят дуги до вершин 2, 4, 5, 7, 8.

Считаем дуги длины не более 2:


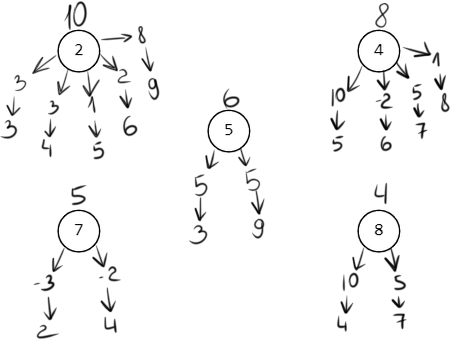
𝑑^≤2(2⁾ = min⁽10; 5 - 3⁾ = 2

𝑑^≤2(3⁾ = min⁽∞; 10 + 3; 6 + 5⁾ = 11

𝑑^≤2(4⁾ = min⁽8; 10 + 3; 5 – 2; 4 + 10⁾ = 3

𝑑^≤2(5⁾ = min⁽6; 10 + 1; 8 + 10⁾ = 6

𝑑^≤2(6⁾ = min⁽∞; 10 + 2; 8 – 2⁾ = 6

𝑑^≤2(7⁾ = min⁽5; 8 + 5; 4 + 5⁾ = 5

𝑑^≤2(8⁾ = min⁽4; 8 + 1⁾ = 4

𝑑^≤2(9⁾ = min⁽∞; 10 + 8; 6 + 5⁾ = 7

Обновились пути до вершин 2,3,4,9

1. 
   Считаем дуги длины не более 3:
   

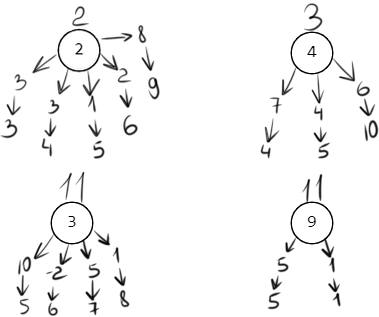
𝑑^≤3(3⁾ = min⁽11; 2 + 3⁾ = 5

𝑑^≤3(4⁾ = min⁽3; 2 + 3; 11 + 7⁾ = 3

𝑑^≤3(5⁾ = min⁽6; 2 + 1; 11 + 4; 10 + 3; 11 + 5⁾ = 6

𝑑^≤3(6⁾ = min⁽6; 2 + 2; 3 - 2⁾ = 1

𝑑^≤3(7⁾ = min⁽5; 3 + 5⁾ = 5

𝑑^≤3(8⁾ = min⁽4; 1 + 3; 11 + 1⁾ = 4

𝑑≤3(9) = min(11; 8 + 2) = 10

𝑑≤3(10) = min(∞; 11 + 6) = 17

Обновился путь до вершин 3,6,9,10

2. 
   Считаем дуги длины не более 4:
   

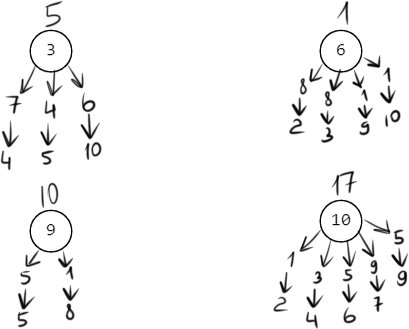
𝑑^≤4(2⁾ = min⁽2; 1 + 8; 1 + 17⁾ = 2

𝑑^≤4(3⁾ = min⁽5; 1 + 8⁾ = 5

𝑑^≤4(4⁾ = min⁽3; 7 + 5; 3 + 17⁾ = 3

𝑑≤4(5) = min(6; 4 + 5; 5 + 10) = 6

𝑑≤4(6) = min(1; 5 + 17) = 1

𝑑≤4(7) = min(5; 9 + 17) = 5

𝑑≤4(8) = min(4; 1 + 10) = 4

𝑑≤4(9) = min(10; 1 + 1; 5 + 17) = 2

𝑑≤4(10) = min(17; 6 + 5; 1 + 1) = 2

Обновился путь до вершин 9, 10

3. 
   Считаем дуги длины не более 5:
   

𝑑^≤5(2⁾ = min⁽2; 2 + 1⁾ = 2

𝑑^≤5(4⁾ = min⁽3; 3 + 2⁾ = 3

𝑑≤⁵(5) = min(6; 5 + 2) = 6

𝑑≤⁵(6) = min(1; 5 + 2) = 1

𝑑≤⁵(7) = min(5; 9 + 2) = 5

𝑑≤⁵(8) = min(4; 1 + 2) = 3

𝑑≤⁵(9) = min(2; 5 + 2) = 2
Обновился путь до вершины 8

4. 
   Считаем дуги длины не более 6:
   
   

𝑑^≤6(4⁾ = min⁽3; 10 + 3⁾ = 3

𝑑^≤6(7⁾ = min⁽5; 5 + 3⁾ = 5
Ни один путь не изменился. Все кратчайшие пути найдены. Дерево кратчайших путей:

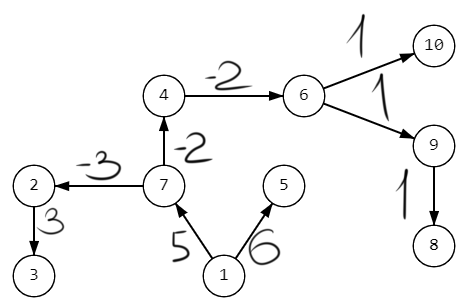
Список использованных источников

Гисин, В. Б. Дискретная математика : учебник и практикум для вузов / В. Б. Гисин. — Москва : Издательство Юрайт, 2021. — 383 с. — (Высшее образование). — ISBN 978-5-534-00228-7. — Текст : электронный // Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/468980 (дата обращения: 03.11.2021).

2. 
   Палий, И. А. Дискретная математика и математическая логика : учебное пособие для вузов / И. А. Палий. — 3-е изд., испр. и доп. — Москва : Издательство Юрайт, 2021. — 370 с. — (Высшее образование). — ISBN 978- 5-534-12446-0. — Текст : электронный // Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/472909 (дата обращения: 03.11.2021).
   
3. 
   Скорубский, В. И. Математическая логика : учебник и практикум для вузов / В. И. Скорубский, В. И. Поляков, А. Г. Зыков. — Москва : Издательство Юрайт, 2021. — 211 с. — (Высшее образование). — ISBN 978-5-534-01114-2.
   

— Текст : электронный // Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/469864 (дата обращения:03.11.2021).

2. 
   Судоплатов, С. В. Дискретная математика : учебник и практикум для вузов / С. В. Судоплатов, Е. В. Овчинникова. — 5-е изд., испр. и доп. — Москва
   

: Издательство Юрайт, 2021. — 279 с. — (Высшее образование). — ISBN 978- 5-534-00871-5. — Текст : электронный // Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/468700 (дата обращения: 03.11.2021).