Метод сопряженного градиента. Перевод. Краткий обзор в этой статье эффективный gv1cgметод разработан для оптимизации модифицированного алгоритма сопряженного градиента с использованием нового свойства сопряженности.
 Скачать 1.5 Mb. Скачать 1.5 Mb.
|
|
Оптимизация Модифицированного Алгоритма Сопряженного Градиента Amel Nashat Shakir Краткий обзор В этой статье эффективный GV1-CG-метод разработан для оптимизации модифицированного алгоритма сопряженного градиента с использованием нового свойства сопряженности. Это делается для увеличения скорости сходимости и сохранения характерной массовой сходимости с использованием свойства сопряженности. Используемое свойство предлагается для публичных функций, поскольку оно не обязательно должно быть квадратичной и выпуклой функцией. Было доказано свойство резкости спуска и всесторонняя сходимость для предлагаемого улучшенного алгоритма. Численные результаты по тестовой функции указывают на то, что новый CG-метод превосходит многие аналогичные методы в этой области. Ключевые слова: сопряженный градиент, развитое свойство сопряжения, улучшенный алгоритм, оптимизация, глобальная сходимость, направление спуска. Вступление Наш интерес к методам сопряженного градиента обусловлен двумя причинами. Во-первых, эти методы являются одними из старейших и лучших методов решения систем линейных уравнений больших размеров. Во-вторых, эти методы могут быть адаптированы для решения задач нелинейной оптимизации [13]. Существует два типа этих методов. Первый тип – это метод линейного сопряжения, который также известен как метод квадратичного сопряжения. Иногда его называют чистым сопряженным градиентом, и он используется для минимизации выпуклой квадратичной функции. Второй тип известен как метод нелинейного сопряженного градиента, известный как неквадратичный сопряженный градиент, используемый для минимизации общей выпуклой функции или нелинейных функций. Метод линейного сопряжения был впервые предложен Хестенесом и Штифелем в 1952 году как итерационный метод, который первоначально использовался в качестве альтернативы методу Гаусса. Его целью было решение больших линейных систем с матрицей положительных параметров на компьютере [10]. И Флетчер, и Ривз разработали метод Хестенеса и Штифеля, а метод сопряженного градиента был первоначально введен в 1960. Это один из первых известных методов решения задач нелинейной оптимизации больших размеров. На протяжении многих лет было предложено много различных методов в соответствии с оригинальной формулой этого метода, некоторые из которых широко используются в практическом применении [13]. Типы методов сопряженного градиента 2.1. Классические методы Сопряженного Градиента Метод линейного сопряженного градиента — это итерационный метод решения проблемы миниатюризации: 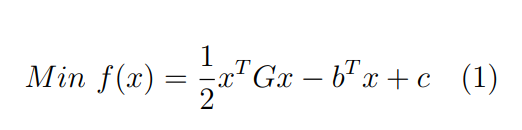 Здесь 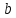 представляет собой постоянный вектор, представляет собой постоянный вектор,  – константное значение, а – константное значение, а 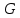 – это положительная симметричная матрица типа n × n. – это положительная симметричная матрица типа n × n.Уравнение (1) может быть получено эквивалентным образом в виде системы линейных уравнений следующим образом: Это означает, что единственное решение для уравнения (1) является таким же решением для системы (2). Таким образом, мы можем подготовить метод градиентного сопряжения либо в алгоритме для решения линейных систем, либо для нахождения наименьшего значения для выпуклых квадратичных функций [14]. Отметим, что градиент функции 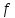 равен остатку, который является отрицательным градиентом линейной системы, т.е.: равен остатку, который является отрицательным градиентом линейной системы, т.е.: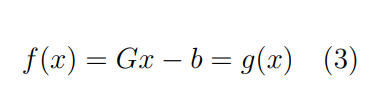 и когда 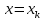 : :Кроме того, метод сопряженного градиента обладает способностью генерировать набор векторов со свойством сопряженности, заключающимся в том, что он может вычислять новое направление 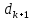 , используя предыдущее направление , используя предыдущее направление 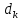 и текущий градиент и текущий градиент 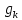 . Он также выбирает линейную композицию направления крутого спуска ( . Он также выбирает линейную композицию направления крутого спуска (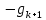 предыдущее направление предыдущее направление 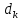 , нам не нужно знать все предыдущие направления , нам не нужно знать все предыдущие направления 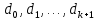 для множества сопряжения; где для множества сопряжения; где 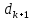 – сопряжение со всеми предыдущими направлениями). Это свойство делает этот метод требующим большого пространства и вычислений: – сопряжение со всеми предыдущими направлениями). Это свойство делает этот метод требующим большого пространства и вычислений: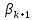 представляет числовую величину, а представляет числовую величину, а 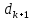 и и 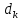 сопряжены с матрицей сопряжены с матрицей 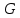 . .Выбирается первое направление поиска в начальной точке 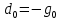 [13]. Тогда скорость сходимости линейна, если не извлекается итерация [15]. [13]. Тогда скорость сходимости линейна, если не извлекается итерация [15]. Метод сопряженного градиента может быть расширен для включения общих нелинейных функций с использованием ряда Тейлора в аппроксимации функции. Это используется для того, чтобы показать ранг целевой функции. Вблизи решения эти функции ведут себя аналогично квадратичным функциям [9]. Алгоритм (1) (Классический метод сопряженного градиента) Существует много шагов для алгоритма (1), и они суммируются в следующее: Выбрав 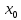 , установить , установить 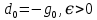 и и 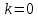 . .Вычисление длины шага 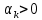 , удовлетворяющей поиску по линии Вольфе , удовлетворяющей поиску по линии Вольфе 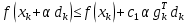 и и 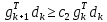 , где , где 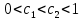 . .Вычислить 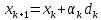 , если , если 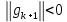 , то остановиться. , то остановиться.Вычислить 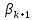 и сгенерировать тренд и сгенерировать тренд 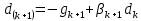 . .Назначить 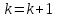 , а затем перейдите к шагу 2. , а затем перейдите к шагу 2.Соответствующие градиентные алгоритмы различаются в зависимости от выбора различных параметров 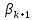 на шаге 4, и наиболее популярные формулы обобщены в следующей таблице: на шаге 4, и наиболее популярные формулы обобщены в следующей таблице: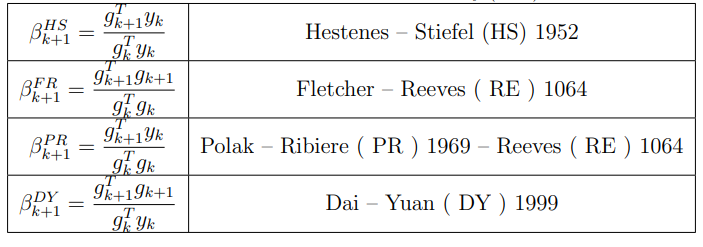 Таблица 1. Параметры модели оценки методом (OLS) 2.2. Свойства классических алгоритмов сопряженного градиента Методы сопряженного градиента обладают следующими свойствами, когда целевая функция является квадратичной функцией, а линейный поиск является точным: Сопряженность 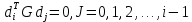 Ортогонально 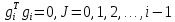 Спуск 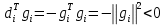 Точный поиск строки, ELS 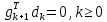 Свойство квадратичного завершения [18]. Множители, требующие 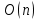 вычислений для каждого повторения приближения к минимуму, означающему, что существует глобальная конвергенция алгоритмов) [9]. вычислений для каждого повторения приближения к минимуму, означающему, что существует глобальная конвергенция алгоритмов) [9].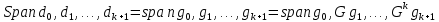 , используя методы сопряженного градиента (подпространство Крылова) [5]. , используя методы сопряженного градиента (подпространство Крылова) [5].Глобальная конвергенция метода спуска Пусть 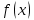 – непрерывная функция, непрерывно дифференцируемая и регулярная в выпуклом множестве: – непрерывная функция, непрерывно дифференцируемая и регулярная в выпуклом множестве: 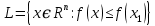 . Таким образом, . Таким образом, 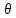 — это угол между направлением поиска — это угол между направлением поиска 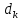 и и 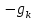 . .Тогда 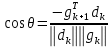 , где , где 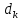 удовлетворяет свойству спуска. Также последовательность, генерируемая выражением удовлетворяет свойству спуска. Также последовательность, генерируемая выражением 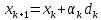 , сходится к критической точке , сходится к критической точке 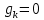 или или 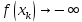 или или 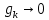 , если , если 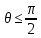 и линейный поиск – это множество [12]. и линейный поиск – это множество [12].2.3. Метод параметрического Сопряженного Градиента Алгоритм сопряженного градиента для параметра был определен таким же образом, как были собраны квази-ньютоновские методы для получения семейств Бройдена или Хуанга. Эти алгоритмы были определены как 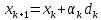 и и 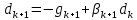 , где параметрический , где параметрический 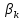 найден, например: [4] найден, например: [4]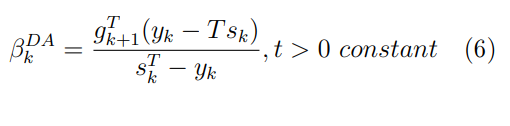 или [6] 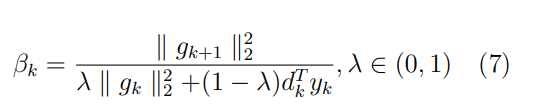 Этот метод был недавно расширен Дай и Юанем для интервала 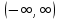 [7]. [7].2.4. Модифицированные методы Сопряженного Градиента Методы сопряженного градиента важны в области, поскольку они имеют неявную связь с квази-ньютоновскими методами. Эти методы имеют аппроксимировано квадратичную скорость. Если целевая функция квадратична и линейна, поиск является точным. Таким образом, скорость линейно возрастает в общей функции. Для преодоления проблем квази-ньютоновских методов требуется матрица и большая арифметическая операция. Кроме того, требуется увеличить скорость сходимости сопряженных методов векторов. Таким образом, это стало толчком для модифицированной версии алгоритмов сопряжения. Шеннон использует формулу BFGS, которая является квази-ньютоновской, как в (8). Здесь это 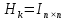 и вычисляется следующим образом: [17]. и вычисляется следующим образом: [17].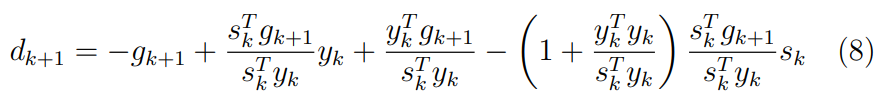 Этот метод называется BFGS без памяти (memory less). В 2010 году Аббо предложил в его диссертации [1] другой метод сопряженных градиентных методов, называемый V1–CG: 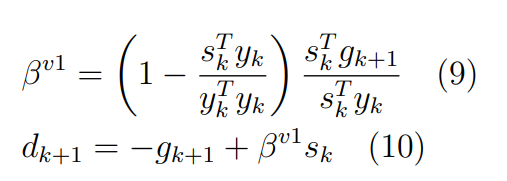 Шейкер (2015) обобщил модифицированный сопряженный градиент [16], который был предложен Аббо в 2010 году, названный V1–CG, и достиг следующего результата: 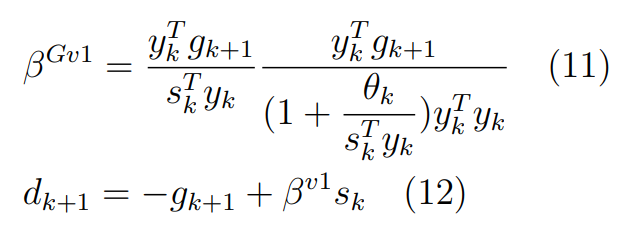 2.5. Улучшенный алгоритм GV1 – CG Цель улучшения 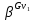 получена от выпуклой квадратичной функции (условия, налагаемые на целевую функцию). В этом разделе мы сосредоточимся на методе GV1– CG, где мы улучшаем это и увеличиваем скорость сходимости при сохранении свойства глобальной сходимости [1]. Это достигается путем обобщения общей функции, которая не обязательно должна быть квадратичной функцией и выпуклой. Это обобщение предназначено для улучшения этого метода, и мы используем разработанное свойство сопряженности из работы Дай, Ляо [8]. получена от выпуклой квадратичной функции (условия, налагаемые на целевую функцию). В этом разделе мы сосредоточимся на методе GV1– CG, где мы улучшаем это и увеличиваем скорость сходимости при сохранении свойства глобальной сходимости [1]. Это достигается путем обобщения общей функции, которая не обязательно должна быть квадратичной функцией и выпуклой. Это обобщение предназначено для улучшения этого метода, и мы используем разработанное свойство сопряженности из работы Дай, Ляо [8].Здесь условие Липшица 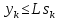 и при и при 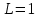 , где , где 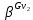 может быть записано следующим образом: может быть записано следующим образом: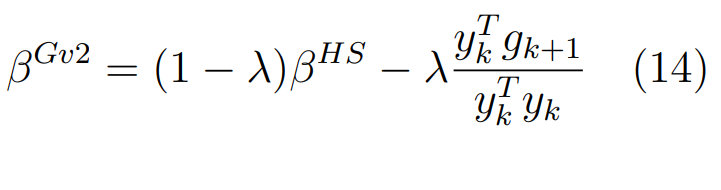 где направления спуска алгоритма равны Здесь мы умножаем обе стороны на 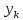 и, используя уравнение (13), находим λ следующим образом: и, используя уравнение (13), находим λ следующим образом: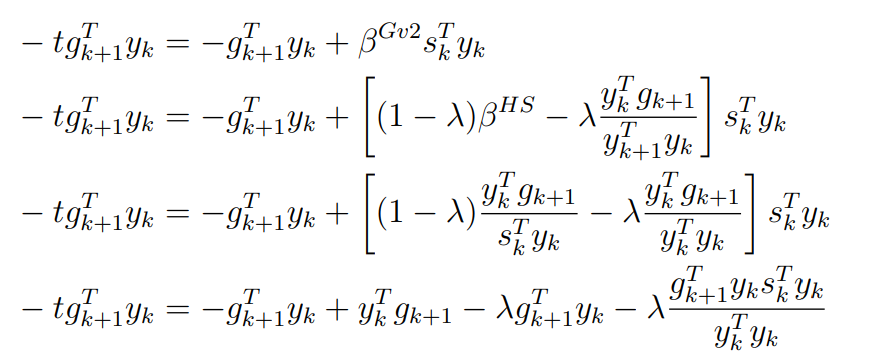 разделите обе стороны на 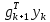 для получения: для получения: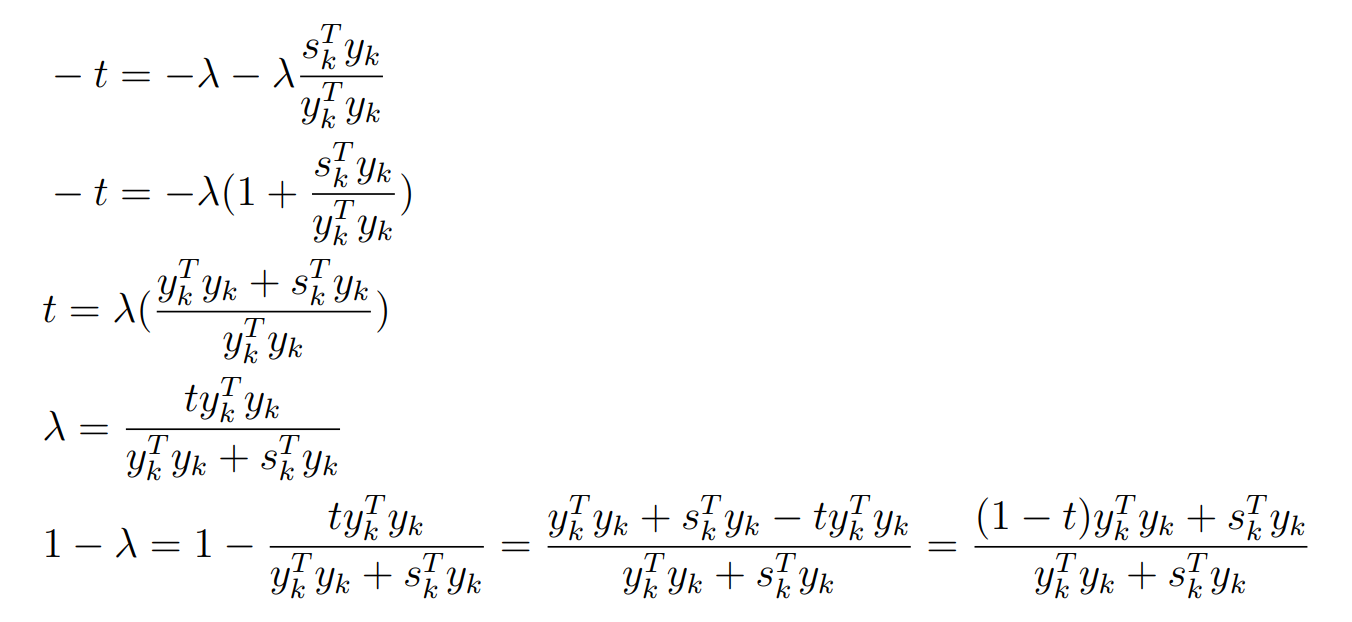 для подставленных 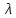 и и 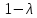 в уравнении (14) находим в уравнении (14) находим 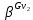 следующим образом следующим образом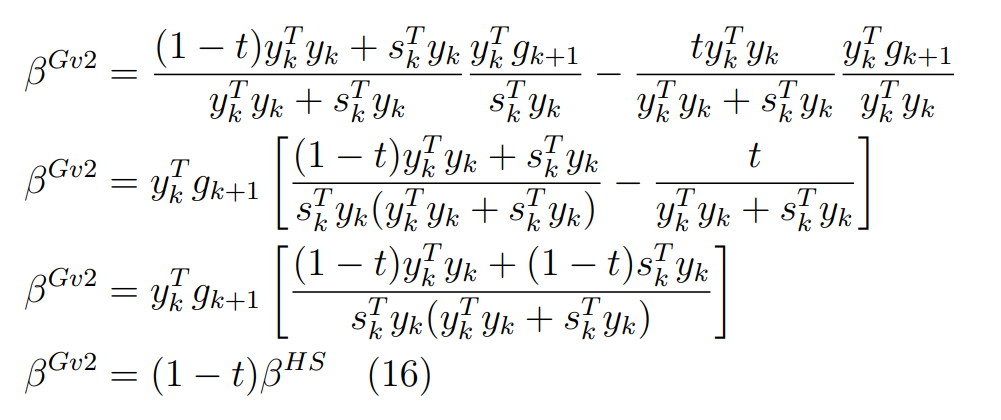 Здесь t – это положительная величина, определяемая следующим образом: 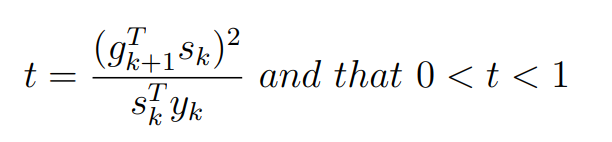 Следовательно, конечное значение 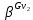 после подстановки t выглядит следующим образом: после подстановки t выглядит следующим образом: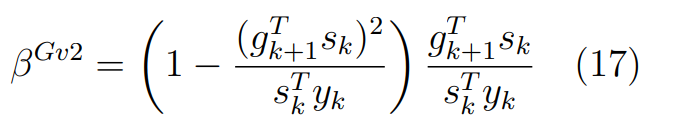 Ясно, что уравнение (17) указывает на взаимосвязь между 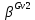 и и 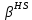 и и 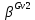 — это величина, умноженная на — это величина, умноженная на 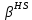 . .Следовательно, мы можем определить направление поиска нового улучшенного алгоритма следующим образом: 2.5.1. Свойство спуска для алгоритма GV2-CG Теорема 1. Теорему 1 можно объяснить следующим образом. В теореме, 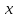 удовлетворяет условию Вольфе удовлетворяет условию Вольфе 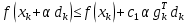 и и 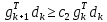 , где , где 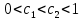 и и 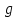 удовлетворяет условию Липшица удовлетворяет условию Липшица 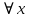 и что и что 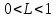 , в то время как , в то время как 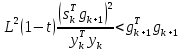 верно. Тогда GV2-CG алгоритм выполняет свойство спуска. верно. Тогда GV2-CG алгоритм выполняет свойство спуска.Доказательство. Чтобы доказать теорему, мы следуем индукции. Для начального направления ( 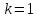 ) есть ) естьПолагая 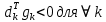 . .Доказывая 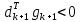 , тогда , тогда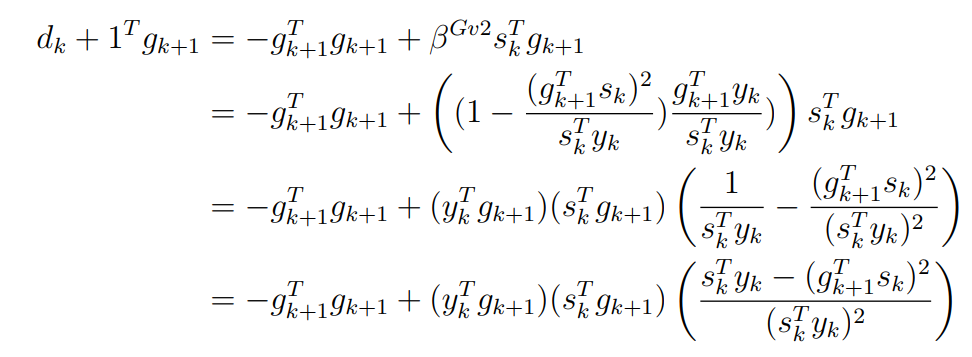 Из условия Лейпцига 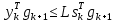 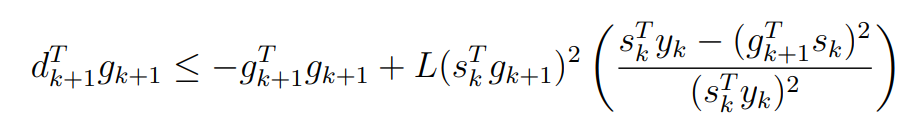 Так что, мы находим 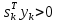 из условия Вольфе, из условия Вольфе, 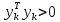 и и 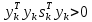 и при размещении их в приведенном выше уравнении получаем: и при размещении их в приведенном выше уравнении получаем: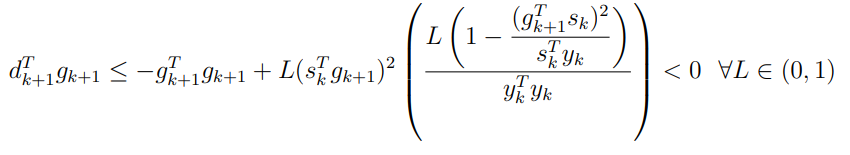 так что 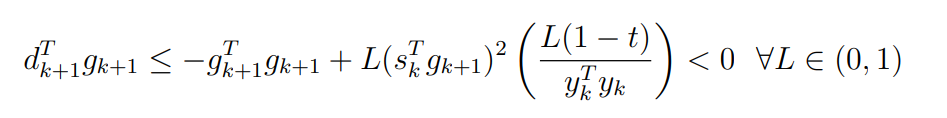 где 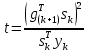 и, следовательно, и, следовательно, 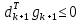 . .Следовательно, направление поиска, полученное в результате алгоритма GV2-CG, является направлением спуска для 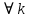 . .2.5.2. Глобальная конвергенция GV2-CG Теорема 2. В теореме 2 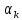 удовлетворяет условиям Вольфе и удовлетворяет условиям Вольфе и 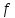 ограничено ниже, в то время как ограничено ниже, в то время как 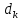 является направлением спуска для является направлением спуска для 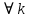 , то есть , то есть 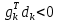 . Кроме того, . Кроме того, 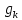 удовлетворяет условию Лейпцига в открытом множестве удовлетворяет условию Лейпцига в открытом множестве  , содержащем множество уровней L, так что , содержащем множество уровней L, так что  , где , где  - начальная точка, тогда алгоритм (GV2-CG) может остановиться в стационарной точке, т.е. - начальная точка, тогда алгоритм (GV2-CG) может остановиться в стационарной точке, т.е.  или или 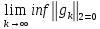 . .Доказательство. Эта теорема доказывается противоречием, т.е. если теория неверна 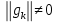 , то существует положительная константа , то существует положительная константа 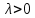 : :тогда 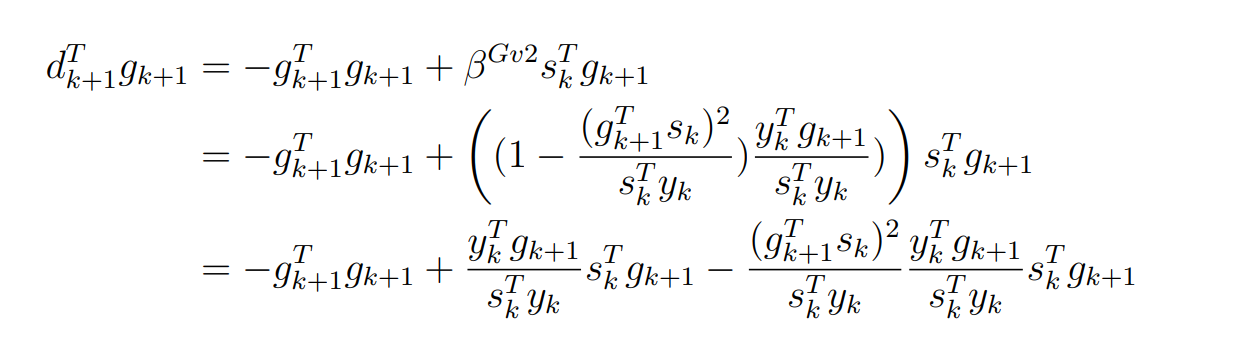 Второе условие Вольфе 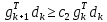 для для 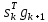 и условие Лейпцига используются для: и условие Лейпцига используются для: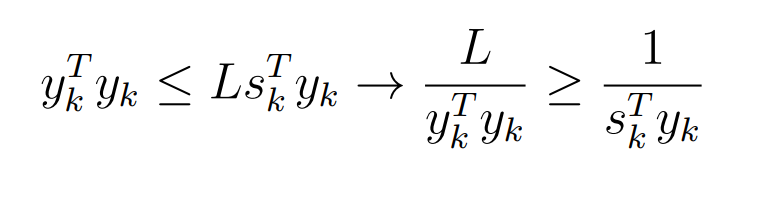 Следовательно: 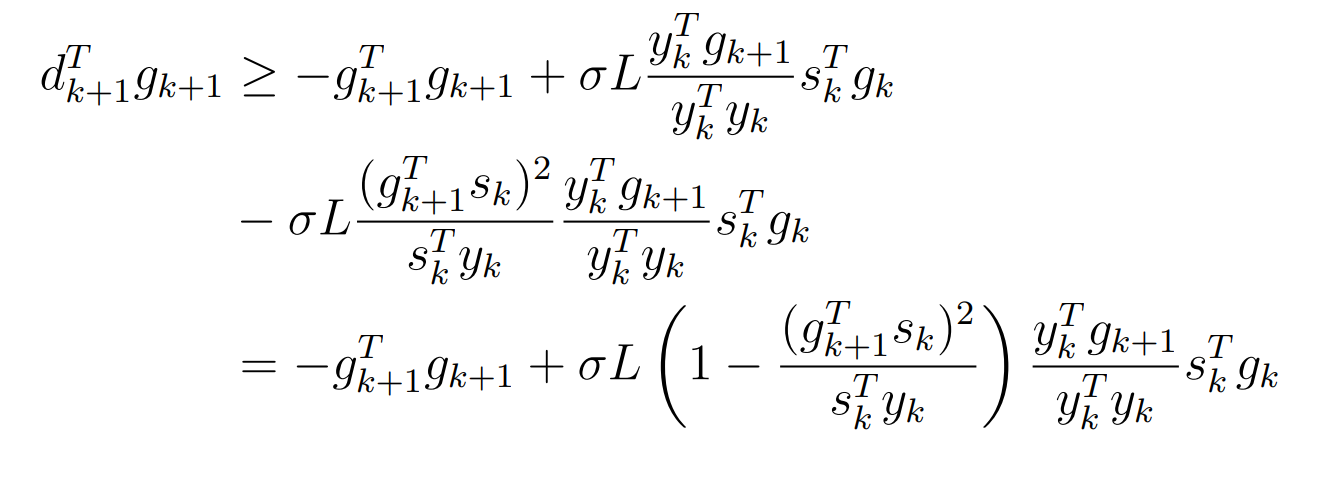 мы имеем: 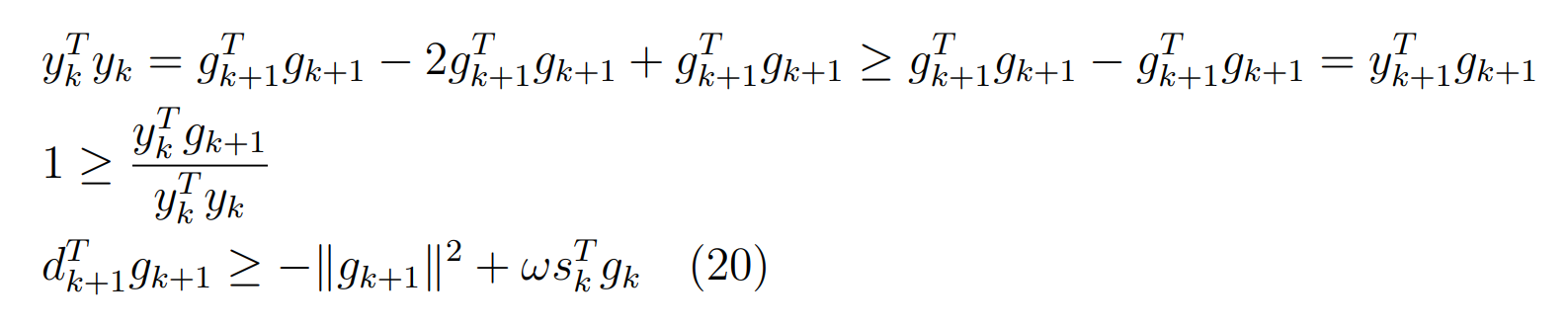 когда 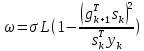 разделим обе стороны (20) на разделим обе стороны (20) на 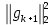 и, возведя в квадрат, мы получаем: и, возведя в квадрат, мы получаем: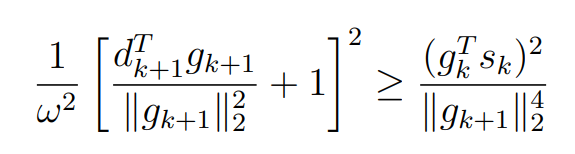 Затем мы умножаем обе стороны на 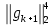 и используем факт и используем факттогда 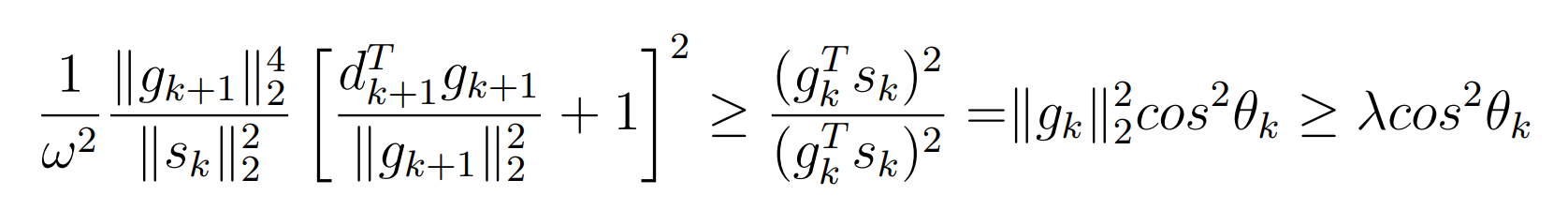 Затем вычисляется сумма для 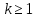 : :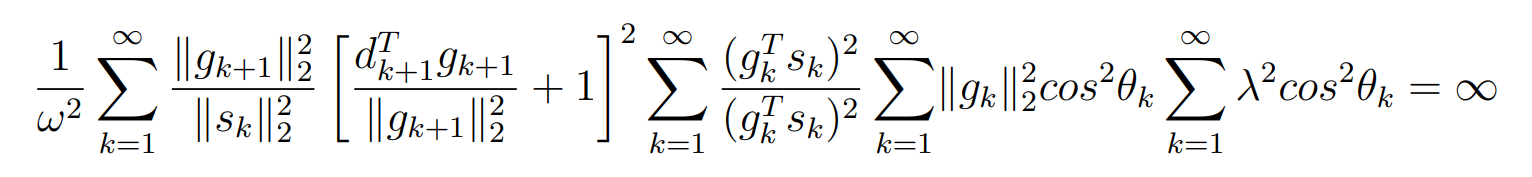 Противоречие с условием Зутендейка [19], следовательно, 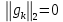 или или 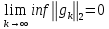 . .3. Численные Эксперименты В этом параграфе выполненная реализация FORTRAN для нового алгоритма GV2-CG, который выполняется на наборе неконструктивных оптимизирующих тестовых задач [3]. Затем мы выбрали (10) формы крупномасштабных тестовых задач (см. Приложение). Для каждой функции существует ряд переменных для численных экспериментов при 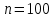 и и 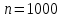 . За этим следует сравнение производительности алгоритма GV2-CG, упомянутого в уравнении (17), с алгоритмом GV1-CG, упомянутым в уравнении (11) [11]. . За этим следует сравнение производительности алгоритма GV2-CG, упомянутого в уравнении (17), с алгоритмом GV1-CG, упомянутым в уравнении (11) [11].Эти алгоритмы в условиях поиска по линии Вольфе реализованы с 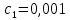 и и 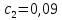 , где начальный размер шага , где начальный размер шага 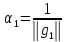 и начальное предположение для других итераций, т.е. и начальное предположение для других итераций, т.е. 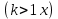 ; ;  . .Критерием остановки всех случаев является  , а максимальное количество итераций равно 2000. , а максимальное количество итераций равно 2000.Наше сравнение включает в себя следующее: NOI: количество итераций. FGN: количество оценок функции и градиента, которые одинаковы в этих алгоритмах. LINS: номер подпрограммы поиска вызывающей линии. В таблице (2) приведены численные результаты для использования (10) тестовых функций при  , а таблица (3) показывает числовые результаты с использованием (10) тестовых функций, когда , а таблица (3) показывает числовые результаты с использованием (10) тестовых функций, когда  . .В таблице (4) приведено сравнение процентной доли нового алгоритма с GV1-CG при  и когда NOI; FGN и LINS принимают инструменты GV1-CG за 100%. и когда NOI; FGN и LINS принимают инструменты GV1-CG за 100%.В таблице (5) показано то же сравнение, что и в таблице (4), но, когда  . . Таблица 2. Сравнение между методами (ШУМ; FGN & LINS) для общего числа (10) задач с n = 100  Таблица 3. Сравнение между методами (ШУМ; FGN & LINS) для общего числа (10) задач с n = 1000 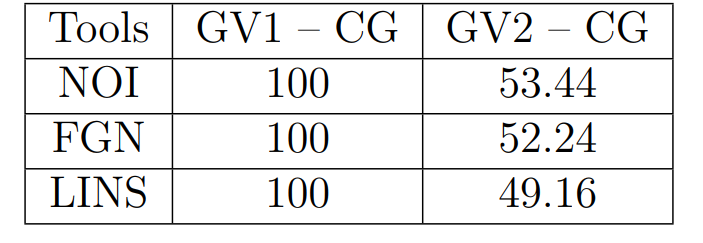 Таблица 4. N = 100 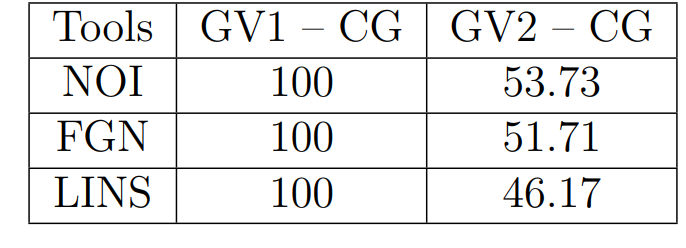 Таблица 5. N = 1000 Рассуждения Таблица (4) показывает, что при 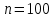 мы принимаем 100% для метода GV1-CG. Новый метод (GV2-CG) является улучшенной версией для (47)% NOI; (48)% FGN; (51)% LINS. мы принимаем 100% для метода GV1-CG. Новый метод (GV2-CG) является улучшенной версией для (47)% NOI; (48)% FGN; (51)% LINS.Кроме того, в таблице (5) 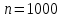 со 100% для метода GV1-CG. Предлагаемый способ (GV2-CG) является улучшением для (47)% NOI; (49)% FGN; (54)% LINS. со 100% для метода GV1-CG. Предлагаемый способ (GV2-CG) является улучшением для (47)% NOI; (49)% FGN; (54)% LINS.В целом, результаты показывают, что новый алгоритм в целом показал значительные улучшения. Приложение 1 - Расширенная Штрафная Функция 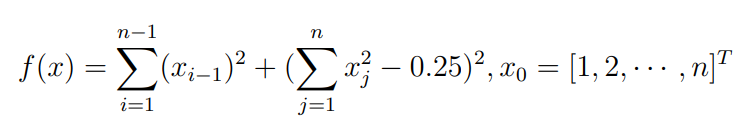 2 - DENSCHNA Функция 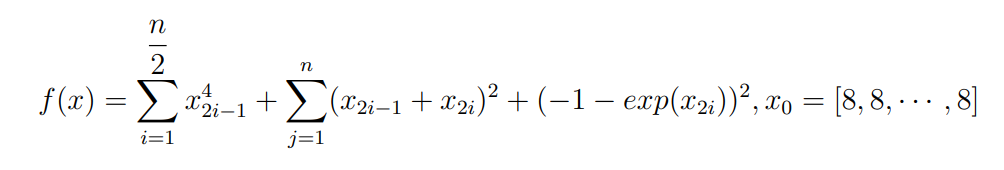 3 - Диагональ 3 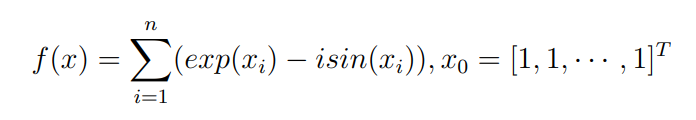 4 – Расширение функции Пауэлла 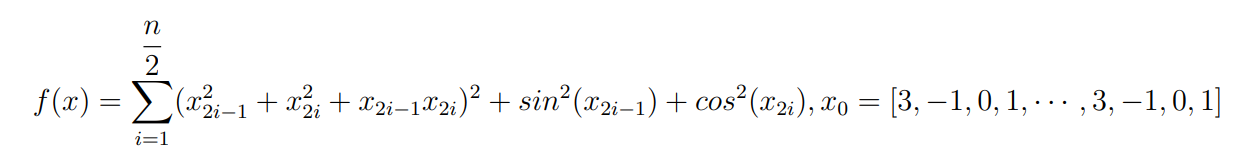 5 - Расширенная функция Химмельблана 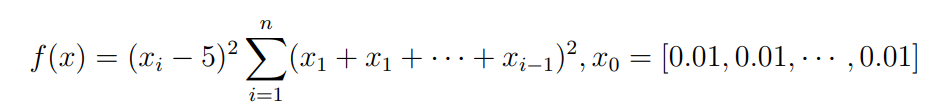 6 – Возмущенная Квадратичная Диагональ 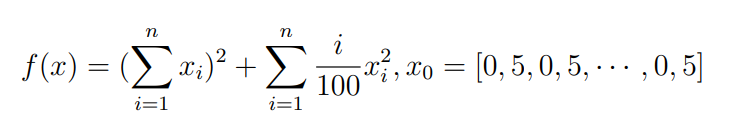 7 – Обобщенная Трехдиагональная 2 функция (Generalized Tridiagonal 2 Function) 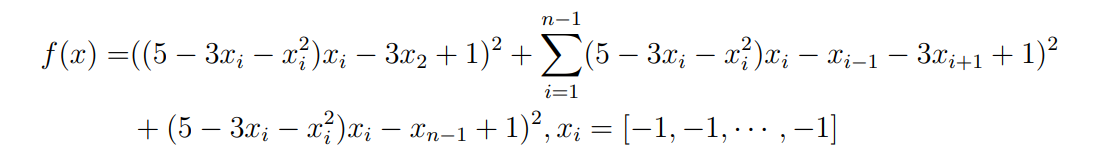 8 - Расширенная функция Клиффа 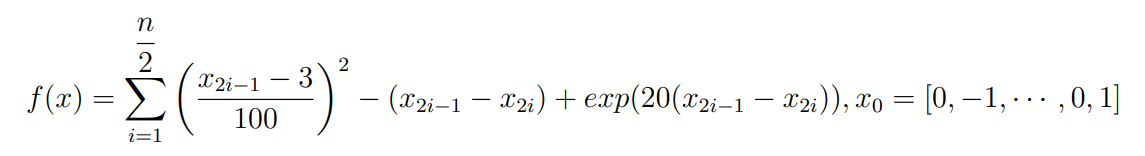 9 – Почти Возмущенный Квадратичный (Almost Perturbed Quadratic) 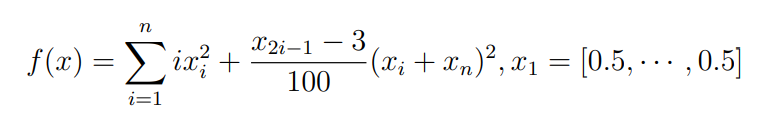 10 – ENGVALI функция (CUTE) 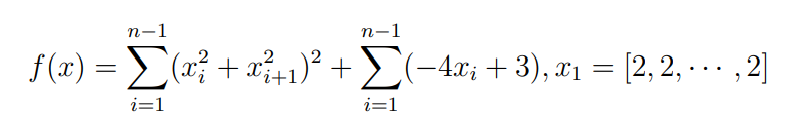 Список источников K.K. Abbo, Developing of Gradient Algorithm for Solving Unconstrained Non-Linear Problem with Artificial Neural Networks, Doctoral thesis Faculty of Computing and Mathematics University of Mosul Sciences, (2010). N. Andrei, Conjugate Gradient Algorithms for Molecular Formation under Pair Wise Potential Minimization, Center for Advanced Modeling and Optimization, (2007c). N. Andrei, An Unconstrained Optimization Test Function collection, Advance Model Optimization, Vol. (10), (2008) 147 -161 . A.G. Buckley, A combined Conjugate Gradient Quasi – Newton Minimization Algorithm. Math, Prog. 15, (1987) 200 – 210. E.K.P. Chong and S.H. Zak, An Introduction to Optimization, Jon Wiley & Sons, Inc., Canada (2001). Y. Dai and Y. Yuan,A three Parameter family of hybrid conjugate gradient method, Mathematics of Computation, 70, (2001). Y. Dai and Y. Yuan, An Extended Class of Non – Linear CG Methods, to appear, Fifth International Conference of Optimization, Hong – Kong (2010). Y. Dai and L.Z. Liao, New Conjugacy Conditions and Related Non- Linear Conjugate Gradient Methods, Applied Mathematics and Optimization, Springer – Verlag, 43, New York, USA (2001)87- 101. R. Fletcher, Practical methods of optimization, A Wiley Inter Science Publication, Johan-Wiley & Sons, Inc., New York (1987). M.R. Hestenes and E. Stiefel, Method of Conjugate gradient for solving linear systems, Journal of Research of the National Bureau of Standards, Vol. (5), No. (49), (1952) 409-436. Y. Hiroshi and S. Naoki, Anew Nonlinear Conjugate Gradient Method for Unconstrained Optimization, Journal of the Optimization Research, Vol. (48), No. (4), (2005) 284-296. J. Kinsella, Course Notes for MS4327 Optimization, http://Jkcray. Maths.ul.ie/ms4327/slides.pdf 2011. INT [1], (2009). J. Nocedal and J.S. Wright, Numerical optimization series in operation research, 2nd edition, Springer-Verlag, New York (2006). P. Pedregal, Introduction to Optimization, Springer-Verlag, Inc., New York, USA (2004). M.J.D. Powell, Restart Procedure for conjugate gradient method, Mathematical Programming, 12, (1977) 241- 254. 108 Shakir A.N. Shaker, Development of Modified Conjugate Gradient Algorithm, (2015). D.F. Shanno, On the convergence of a Conjugate Gradient Algorithm, SIAM. J. Number. Anal, 15 (1978). W. Sun and y. Yuan, Optimization Theory and Methods, Nonlinear Programming, Springer Science, Business Media, LIC., New York (2006). G. Zoutendijk, Nonlinear Programming, Computational Methods, In: Integer and Nonlinear Programming, J. Abadie Ed., North – Holland (1970) 37-86. |
