Краткое содержание теоретического материала
 Скачать 71.74 Kb. Скачать 71.74 Kb.
|
|
Пределы и их свойства Обучающийся должен знать: значение математики в профессиональной деятельности и при освоении ППССЗ; основные математические методы решения прикладных задач в области профессиональной деятельности; основы интегрального и дифференциального исчисления. Обучающийся должен уметь: решать прикладные задачи в области профессиональной деятельности. Краткое содержание теоретического материала Теория пределов играет основополагающую роль в математическом анализе, позволяет определить характер поведения функции при заданном изменении аргумента. С помощью предела можно выяснить, имеет ли функция в заданной точке разрыв. Через пределы определяются такие понятия математики как производная, неопределенный и определенный интегралы, составляющие основу дифференциальных уравнений, которые, в свою очередь получили непосредственное применение в медицинской практике. Число а является пределом функции f(x) при х 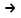 х0 , если для любой последовательности х1,х2,…,хn, сходящейся к числу х0, последовательность f(x1), f(x2),…, f(xn) сходится к числу а х0 , если для любой последовательности х1,х2,…,хn, сходящейся к числу х0, последовательность f(x1), f(x2),…, f(xn) сходится к числу аПри этом употребляют запись 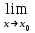 f(x)=а f(x)=аСвойства пределов 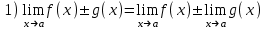 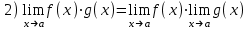 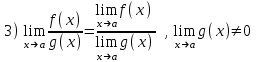 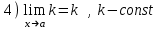 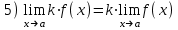 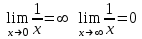 Примеры: 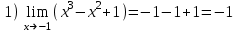 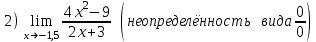 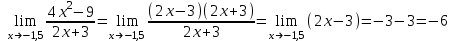 Метод решения: для того, чтобы раскрыть неопределенность, необходимо разложить числитель и знаменатель на множители и сократить на (х – х0) 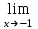 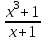 = =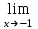 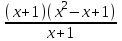 = =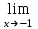 (х2-х+1)=3 (х2-х+1)=33) 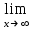 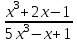 = =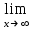  = =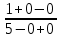 = =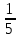 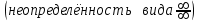 Итак, метод решения следующий: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на х в старшей степени. 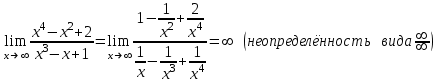 Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности используют метод умножения числителя и знаменателя на сопряженное выражение. 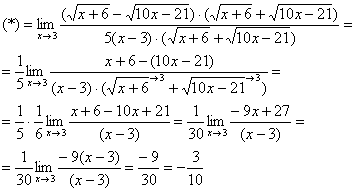 Замечательные пределы: 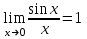 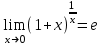 Функция f(x) называется непрерывной в точке хо, если она определена в некоторой окрестности этой точки и если предел функции при х 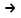 х0равен значению функции в этой точке, т.е. х0равен значению функции в этой точке, т.е.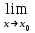 f(x)= f(x0) f(x)= f(x0)Образец решения заданий 1. Найти пределы функций: 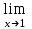 (2х+4)=6 (2х+4)=6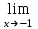 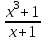 = =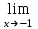 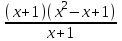 = =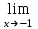 (х2-х+1)=3 (х2-х+1)=3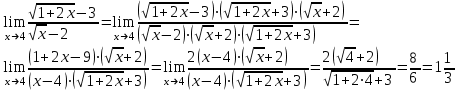 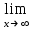 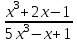 = =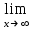  = =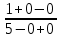 = =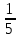 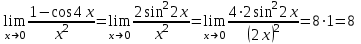 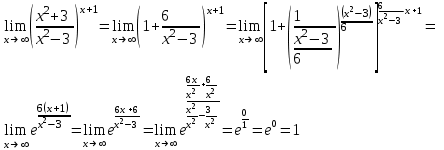 Вопросы к теме Что такое предел функции? Перечислите свойства пределов. С чего начинают решение предела? Назовите виды неопределенностей и способы их раскрытия. Какая функция называется непрерывной? |
