Лекции и практики (1). Курс лекций и материалы для практических занятий

• Название: Курс лекций и материалы для практических занятий
• Дата: 17.03.2023
• Размер: 1.01 Mb.
• Имя файла: Лекции и практики (1).docx
• Тип: Курс лекций; #996812
• страница: 10 из 75

Лекция 3.

ВВЕДЕНИЕ В ЯЗЫК SQL

SQL (Structured Query Language) – это структурированный язык запросов к реляционным базам данных. Базы данных, основанные на реляционной моде- ли данных, являются в настоящее время наиболее широко распространёнными вследствие своей простоты и универсальности методов обработки данных.

Существуют три стандарта SQL [1], принятые ISO (International Standards Organization, Международной организацией по стандартизации): SQL-89 (SQL-1), SQL-92 (SQL-2) и SQL-99/2003 (SQL-3).

Большинство коммерческих систем управления базами данных поддер- живают стандарт SQL-92, который принят ISO в качестве международного стандарта. Многие версии (диалекты) имеют свои отличия, которые касаются, в основном, синтаксиса и некоторых дополнительных возможностей.

SQL является декларативным языком, основанным на операциях реляци- онной алгебры.

1. Операции реляционной алгебры

Операции реляционной алгебры (РА) применимы к реляционным отно- шениям (таблицам). Результатом выполнения операции реляционной алгебры также является отношение, построенное на основе одного или более исходных отношений. Существует пять основных операций РА и три вспомогательных, которые могут быть выражены через основные.

1. 
   Основные операции реляционной алгебры
   

1. 
   Проекция (project).
   

Это унарная операция (выполняемая над одним отношением), служащая для выбора подмножества атрибутов из отношения R. Она уменьшает арность от- ношения и может уменьшить мощность отношения за счёт исключения одина- ковых кортежей.

Пример1. Пусть имеется отношение R(A,B,C) (рис.3.1,а).

Тогда проекция _A,C(R) будет такой, как показано на рис.1,б.

^{ОтношениеR} Проекция _A,C(R)

A B C A C

2. 
   Селекция (select).
   

а) б)

Рис. 3.1. Пример проекции отношения

Это унарная операция, результатом которой является подмножество корте- жей исходного отношения, соответствующих условиям, которые накладывают-

ся на значения определённых атрибутов. Это одна из наиболее часто использу- емых операций SQL.

Пример2. Для отношения R(A,B,C) (рис. 3.2,а) селекция _C=d(R) (при условии "значение атрибута C равно d") будет такой (рис. 2,б):

^{ОтношениеR} Селекция _C=d(R)

A B C A B C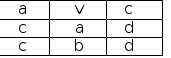



а) б)

Рис. 3.2. Пример селекции отношения

3. 
   Декартово произведение (сartesian product).
   

Это бинарная операция над разносхемными отношениями, соответствующая определению декартова произведения для РМД.

Пример 3. Пусть имеются отношение R(A,B) и отношение S(C,D,E) (рис. 3.3,а).

Тогда декартово произведение RS будет таким (рис. 3.3,б):

^{ОтношениеR ОтношениеS} ДекартовопроизведениеRS

A B C D E A B C D E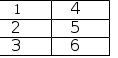



а) б)

Рис. 3.3. Пример декартова произведения отношений

4. 
   Объединение (union).
   

Объединением двух односхемных отношений R и S называется отношение T = R U S, которое включает в себя все кортежи обоих отношений без повторов.

Примечание: имена полей односхемных отношений могут быть разными, достаточно, чтобы совпадало количество полей и типы данных соответствующих полей.

5. 
   Разность (except).
   

Разностью односхемных отношений R и S называется множество кортежей R, не входящих в S.

Пример 4. Пусть имеются отношение R(A,B,C) и отношение S(A,B,C) (рис. 3.4,а). Тогда разность R–S будет такой (рис. 3.4,б):

ОтношениеR ОтношениеS РазностьR–S

A B C A B C A B C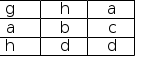



а) б)

Рис. 3.4. Пример разности отношений

2. 
   Вспомогательные операции реляционной алгебры
   

6. 
   Пересечение (intersect).
   

Пересечение двух односхемных отношений R и S есть подмножество корте- жей, принадлежащих обоим отношениям. Это можно выразить через разность:

R ∩ S = R – (R – S).

7. 
   Соединение (join).
   

Эта операция определяет подмножество декартова произведения двух разно- схемных отношений. Кортеж декартова произведения входит в результирую- щее отношение, если для атрибутов разных исходных отношений выполняется некоторое условие соединенияF. Соединение может быть выражено так:

R ⊳⊲ S = _F (R  S)

F

Если условием является равенство значений двух атрибутов исходных отноше- ний, такая операция называется эквисоединением. Естественным называется эквисоединение по одинаковым атрибутам исходных отношений.

Пример 5. Пусть имеются отношения R(A,B,C) и S(A,D,E) (рис. 3.5,а). Тогда естественное соединение R ⊳⊲ S будет таким, как показано на рис. 3.5,б.

ОтношениеR ОтношениеS _{СоединениеR⊳⊲S}

A B C A D E A B C D E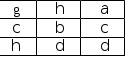



а) б)

Рис. 3.5. Пример естественного соединения отношений

8. 
   Деление (division).
   

Пусть отношение R содержит атрибуты {r₁,r₂,...,r_k, r_k+1,...,r_n}, а отношение S – атрибуты {r_k+1,...,r_n}. Тогда результирующее отношение содержит атрибуты

{r₁,r₂,...,r_k}. Кортеж отношения R включается в результирующее отношение, ес- ли его декартово произведение с отношением S входит в R. Деление может быть выражено так:

R / S = _r1,…,rk (R) – _r1,…,rk ((_r1,…,rk (R)  S) – R).

Пример 6. Пусть имеются отношения R(A,B,C) и S(A,B) (рис. 3.6,а). Тогда частное R/S будет таким как показано на рис. 3.6,б.

	ОтношениеR		ОтношениеS	ЧастноеR/S
A	B C	D	C D	A B

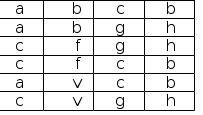а) б)

Рис. 3.6. Пример операции деления