курсовая. ЭНГС_лекции. Курс лекций Томск 2002 Эксплуатация нефтяных и газовых скважин введение общая характеристика нефтяной залежи

• Название: Курс лекций Томск 2002 Эксплуатация нефтяных и газовых скважин введение общая характеристика нефтяной залежи
• Анкор: курсовая
• Дата: 28.02.2023
• Размер: 7.31 Mb.
• Имя файла: ЭНГС_лекции.doc
• Тип: Курс лекций; #960161
• страница: 39 из 97

6.3. Исследование скважин при неустановившихся режимах

Если давление на забое Рс, а тем более пластовое Рк превышает давление насыщения Рнас, то предполагается, что перераспределение давления в пласте после любых возмущений происходит по законам упругого режима. В подземной гидродинамике рассматривается задача притока упругой жидкости к скважине в бесконечном упругом пласте после ее внезапного пуска или остановки. Решением этой задачи является формула

, (6.26)

Физическая интерпретация этой формулы следующая: p{r,t) означает изменение давления в упругом пласте в точке М, удаленной от точки возмущения - скважины на расстояние r через время t после начала возмущения.

В данном случае под возмущением понимается либо пуск скважины с дебитом Q, либо внезапная остановка скважины, работавшей перед этим длительное время, с дебитом Q (Q - расход при стандартных условиях). При пуске скважины давление в точке М уменьшается на P по сравнению с первоначальным, а при внезапной остановке скважины, длительно работавшей с дебитом Q, P - увеличение давления в точке М по сравнению с первоначальным, Еi( - х), где x = r²/4t - специальная табулированная экспоненциальная функция, значения которой можно найти в таблицах специальных функций. Здесь  = k/^x - пьезопроводность, причем ^x - приведенный объемный коэффициент упругости среды (вода, нефть, порода), t - время с момента пуска или остановки скважины.

Решение (6.26) является строго аналитическим, поэтому оно справедливо для любых радиусов и в частности для радиуса r, равного радиусу скважины rс. В этом случае формула (6.26) будет описывать закон изменения давления на стенки самой скважины и является характеристикой процесса «самопрослушивания» скважины. Таким образом, если остановить скважину и зарегистрировать изменение во времени давления на забое скважины, можно будет найти те параметры пласта, при которых закон изменения P(t) совпадет с фактически зарегистрированным. Для практического использования формулу (6.26) несколько упрощают. Дело в том, что при исследовании скважин на неустановившихся режимах, т. е. при самопрослушивании, приходится иметь дело с малыми значениями аргумента x = rc²/4t, так как rс - радиус скважины мал, a t составляет сотни и тысячи секунд.

При малых х экспоненциальная функция



хорошо аппроксимируется логарифмической функцией Ei( - х) = Ln (х) +0,5772,

где 0,5772 - постоянная Эйлера. Поэтому формулу (6.26) можно переписать следующим образом:

, (6.27)

Вводя знак минус в скобки и учитывая, что Ln (e) = 1, можем записать:

.

Но e^0,5772 = 1,781.

Следовательно,



или

. (6.28)

Обычно числовой коэффициент под логарифмом округляют, так что 2,24587 = 2,25. Итак, если остановить скважину, работавшую с дебитом Q, то на ее забое давление начнет повышаться в зависимости от времени t согласно формуле (6.28). При этом предполагают, что режим упругий и давление на забое больше давления насыщения.

На формуле (6.28) основана методика исследования скважины при неустаповившихся режимах. Следует отметить, что формула (6.28) предполагает мгновенную остановку скважины (при t = 0, Q = 0). Это равносильно срабатыванию крана или клапана непосредственно на забое скважины. В действительности остановка, например, фонтанной скважины производится на устье путем закрытия задвижки. В НКТ находится газожидкостная смесь, которая после остановки начнет сжиматься под действием возрастающего забойного давления. В затрубном пространстве также произойдет рост давления и сжатие газовой шапки. Мгновенной остановки скважины не произойдет, а будет продолжающийся последующий затухающий приток жидкости из пласта в скважину, чего формула (6.28) не предусматривает. Поэтому последующий приток является источником некоторых погрешностей, которые возможно исключить путем специальной обработки фактических данных.

Возвращаясь к формуле (6.28), перепишем ее так, чтобы время t было выделено, а именно

. (6.29)

Обозначим:



, (6.30)
, (6.31)



Тогда (V1.29) перепишется так:

.

А это есть уравнение прямой, не проходящей через начало координат.

Отсюда следует правило, что фактически снятая на забое скважины кривая восстановления давления (КВД) Р(t), перестроенная в полулогарифмических координатах y = P, x = Lnt, должна иметь вид прямой отсекающей на оси у ординату а, значение которой определяется формулой (6.30), и имеющей угловой коэффициент b, определяемый формулой (6.31).

КВД на забое скважины записывается регистрирующим скважинным манометром с автономной или дистанционной записью показаний. Такой манометр, спускаемый на забой скважины до ее остановки, дает запись изменения Pс в функции времени t. Поэтому фактическую кривую P(t) необходимо перестроить в координаты P(Lnt) и найти ее постоянные коэффициенты а и b (рис. 6.4). Начальный участок КВД не укладывается на прямую, что связано частично с последующим притоком, о котором было сказано выше, и инерцией масс жидкости, которые вообще не учитываются формулой (6.28).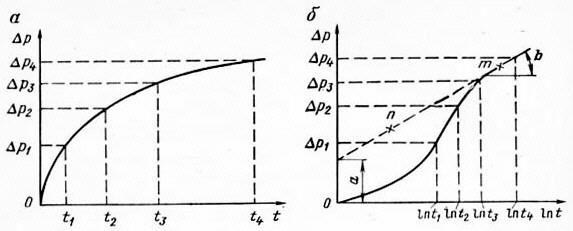



Рис. 6.4. Записанная манометром (а) и перестроенная в полулогарифмические

координаты (б) кривая восстановления давления в остановленной скважине
На перестроенной кривой P(Lnt) отыскивается прямолинейный участок, по двум точкам которого определяется угловой коэффициент

. (6.32)

Вычислив b, можем определить из формулы (6.31) гидропроводность  = kh/:

. (6.33)

Зная , легко найти проницаемость k.

Отрезок а на оси ординат можно получить либо графическим построением, либо аналитически. Из формулы (6.29) имеем



или, подставляя b, получим

, (6.34)

Pi и Lnti - ордината и абсцисса любой точки прямой. Поделив все на b и разложив логарифмы, можно выражение (6.34) переписать следующим образом:



откуда

, (6.35)

(Ln2,25 = 0,80909). Учитывая, что Lnе = 1, можно (6.35) переписать так: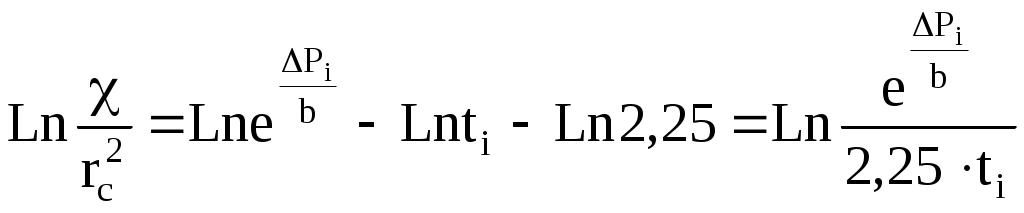



После преобразования получим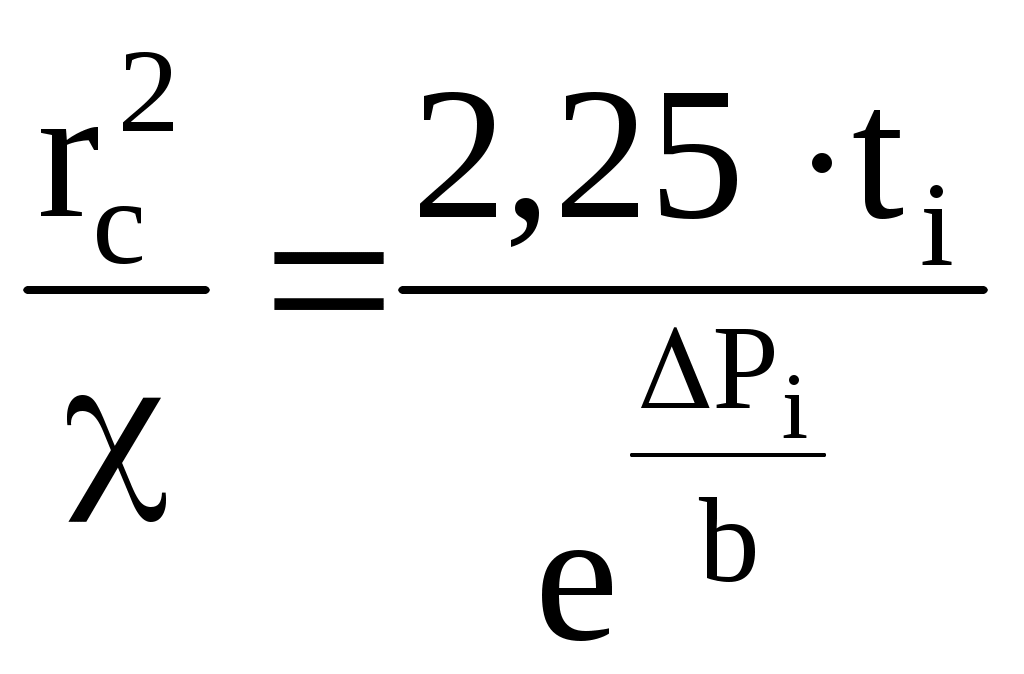

. (6.36)

По формуле (6.36) определяется комплекс . Если по другим данным известна пьезопроводность , то можно определить приведенный радиус скважины rпр, учитывающий гидродинамическое несовершенство скважины, так как известно, что для перехода от совершенной скважины с радиусом rc к несовершенной достаточно подставить вместо радиуса скважины rпр.

Параметры пласта, определенные по КВД описанным методом, характерны для удаленных зон пласта.

Аналогично методом неустановившихся режимов исследуются нагнетательные скважины. Поскольку в нагнетательных скважинах ствол полностью заполнен жидкостью, то погрешности, связанные с явлениями последующего притока, в данном случае не возникают. Кроме того, отсутствие газированного столба жидкости в скважине позволяет измерять давления непосредственно на устье, добавляя к этим показаниям гидростатическое давление столба жидкости в скважине.

Для снятия КВД нагнетательной скважины, работавшей длительное время с дебитом Q, в принципе достаточно на устье закрыть задвижку, т. е. прекратить закачку и снять кривую падения давления P = f(t) на устье. Величина P определяется как разность между давлением на устье при установившемся режиме закачки, т. е. давлением нагнетания, и текущим давлением на устье после прекращения закачки.

Обработка полученных данных для определения пластовых параметров не отличается от описанной выше. Аналитический аппарат для обработки результатов исследования добывающих и нагнетательных скважин на неустановившихся режимах, описанный выше, пригоден и для обработки результатов при ступенчатом изменении дебита на величину Q. Ступенчатое изменение дебита может быть достигнуто сменой штуцера или прикрытием задвижки. При этом скважинным манометром фиксируется КВД P(t) при переходе от начального дебита Q₁ к новому дебиту Q₂, изменившемуся на величину Q = Q₂ - Q_l. В соответствующие формулы вместо Q необходимо подставить Q. В остальном обработка остается прежней.

Аналогичные приемы используются и для так называемого гидропрослушивания пласта. В этом случае в одной скважине вызывается возмущение, т. е. пуск или остановка (начало закачки или прекращение), а в другой - удаленной или в нескольких скважинах - реагирующих фиксируется изменение давления во времени. Для обработки результатов используется также формула (6.26), причем за величину r принимается расстояние между скважинами, за t - время, истекшее с начала возмущения, а за Q - дебит остановленной добывающей или нагнетательной скважины. Поскольку на подобные возмущения удаленные скважины реагируют слабо, то при гидропрослушивании в реагирующих скважинах замеряют изменения статического уровня с помощью опускаемых приборов - пьезографов.

Ранее было отмечено некоторое несоответствие реально протекающего процесса восстановления давления и закрытия скважины, сопровождаемое последующим притоком, с используемым математическим аппаратом, предусматривающим мгновенную остановку скважины. Для устранения этого несоответствия очень многими исследователями были разработаны методы обработки КВД и ряда других дополнительных данных, позволяющих учитывать последующий приток, вносить поправки в линию P(Lnt) и существенно увеличить число точек на прямолинейном участке кривой. Для того чтобы обработать КВД с учетом притока, необходимо знать этот последующий приток в функции времени. Его измеряют хорошо оттарированным и достаточно чувствительным скважинным дебитомером. Однако такие измерения можно произвести только в фонтанных и газлифтных скважинах, в которых НКТ свободны для спуска прибора.

Последующий приток можно определить косвенным путем, хотя и менее точно. Для этого после остановки фонтанной или газлифтной скважины с помощью образцовых манометров записываются изменения давления в затрубном пространстве и на устье скважины. Кроме того, имеется КВД, записанная на забое скважины. Разбивая весь процесс восстановления давления на интервалы по времени и располагая указанными выше данными, которые также разбиваются на те же интервалы по времени, а также зная площади сечения кольцевого пространства и НКТ, можно вычислить объемы жидкости, поступившие в кольцевое пространство и НКТ в течение соответствующего интервала времени. Частное от деления приращения объема жидкости на приращение времени лает расход в данный момент времени. По данным расхода вносится поправка z > 1 в величину P. Это позволяет поднять точки левой, пониженной части кривой P(Lnt и, таким образом, получить большее число точек на прямолинейной части кривой.

Разработано более 30 методов учета последующего притока при исследовании скважин на неустановившихся режимах. Все они достаточно сложны и требуют кропотливой вычислительной и графической работы. Их можно разделить на две группы: дифференциальные методы и интегральные методы.

Первые заключаются в том, что весь процесс восстановления давления разбивается на этапы по времени - шаги, в пределах которых предполагается линейный закон изменения параметров. Для каждого шага вычисляется поправка для Ар.

Вторые также предусматривают разделение процесса на этапы, но при переходе от точки к точке результаты предыдущих шагов суммируются, т. е. интегрируются. Поправка каждой последующей точки определяется с учетом предыдущих шагов. Все методы дают некоторый разброс в результатах, но, как правило, разброс точек при дифференциальных методах значительнее, чем при интегральных.

Исследование на неустановившихся режимах позволяет качественно оценить изменение проницаемости или наличие непроницаемых включений в удаленных областях пласта. Наличие таких аномалий обусловливает вид концевых участков КВД. Увеличение углового коэффициента b на концевых участках соответствует уменьшению проницаемости, уменьшение b - увеличению проницаемости.