курсовая. ЭНГС_лекции. Курс лекций Томск 2002 Эксплуатация нефтяных и газовых скважин введение общая характеристика нефтяной залежи

• Название: Курс лекций Томск 2002 Эксплуатация нефтяных и газовых скважин введение общая характеристика нефтяной залежи
• Анкор: курсовая
• Дата: 28.02.2023
• Размер: 7.31 Mb.
• Имя файла: ЭНГС_лекции.doc
• Тип: Курс лекций; #960161
• страница: 38 из 97

6.2. Исследование скважин при установившихся режимах

В главе 2 была получена формула (2.10) радиального притока жидкости к скважине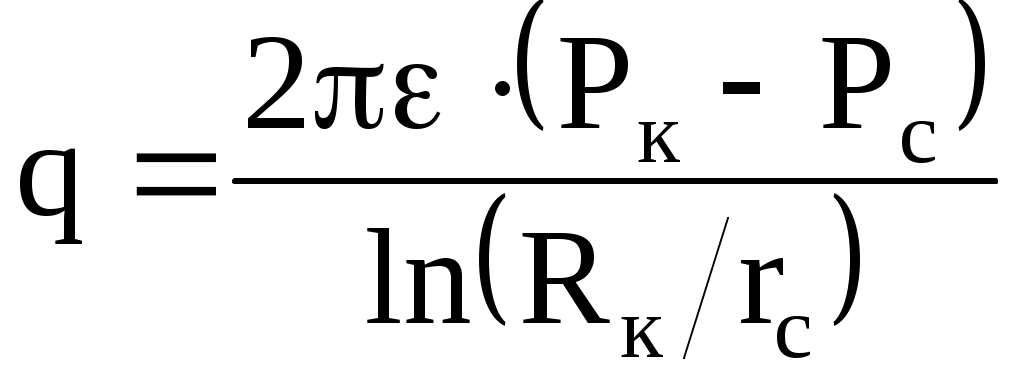

, (6.1)

Если  = (r), то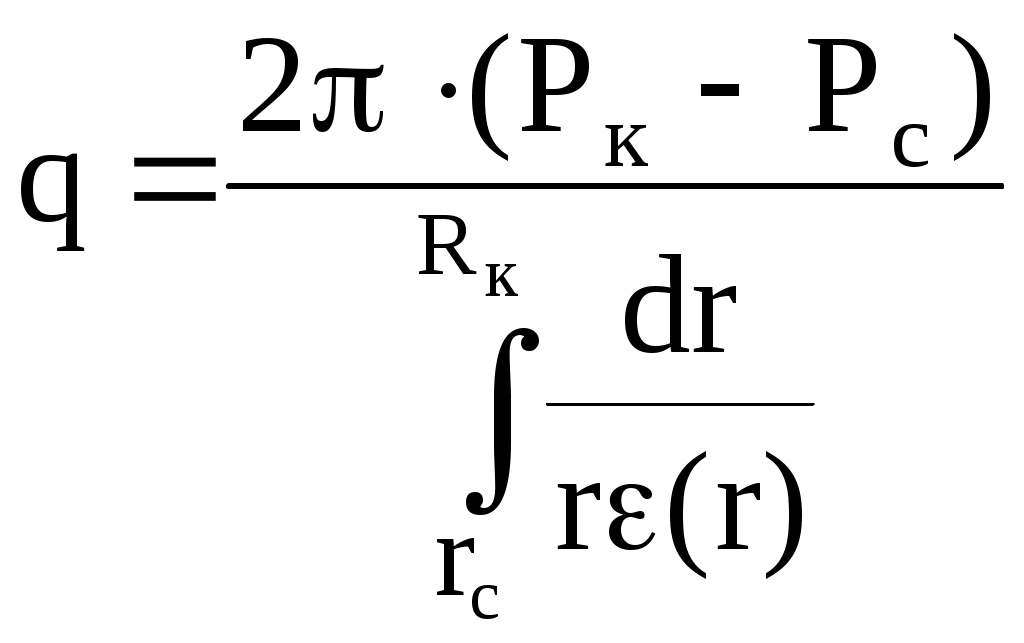

, (6.2)

В главе 4 § 2 было показано, что формулы (4.1) и (4.2), справедливые, строго говоря, для совершенных скважин, остаются справедливыми и для скважин несовершенных (перфорированных), но при подстановке в них вместо радиуса скважины rс приведенного радиуса rпр.

Из формул (6.1) и (6.2) видно, что дебит жидкости q зависит от депрессии Рк - Рс, которая является независимым аргументом. Группу постоянных величин, входящих в эти формулы, можно обозначить А. Таким образом,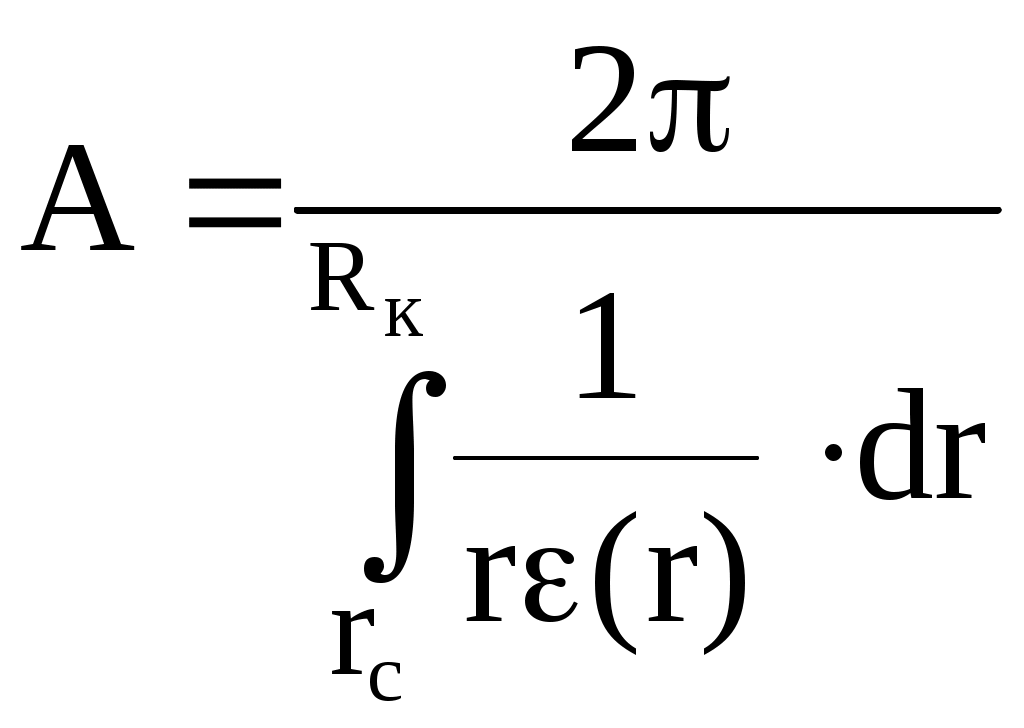

, (6.3)

или

, (6.4)

Тогда дебит будет равен

. (6.5)

Формулы (6.1), (6.2), (6.5) определяют дебит жидкости в пластовых условиях. На практике дебит q измеряется при стандартных условиях и не в объемных единицах, а в т/сут.

Учитывая усадку нефти, т. е. вводя объемный коэффициент bн, и плотность нефти при стандартных условиях ρн, а также переходя от секунд к суткам, можем формулу (6.5) переписать так:

, (6.6)

Введем обозначение

, (6.7)

Тогда

, (6.8)

где Q - дебит скважины при стандартных условиях, т/сут; К - коэффициент продуктивности, т/(сутПа).

Формула (6.8) получила название формулы притока. Из нее видно, что приток линейно зависит от депрессии или при постоянном давлении на контуре от давления на забое скважины. Из (6.8) следует

, (6.9)

т. е. коэффициент продуктивности есть суточный дебит скважины, приходящийся на единицу депрессии. Подставляя в (6.7) значения А из (6.3) и раскрывая значение , можем записать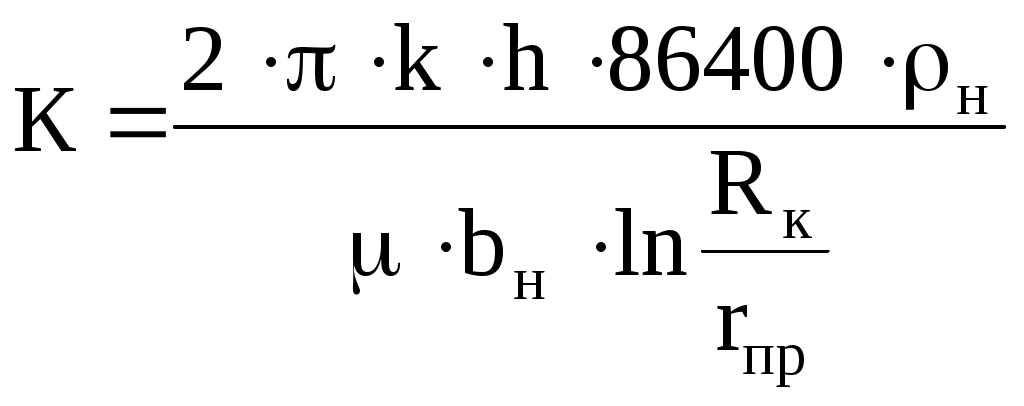

, (6.10)

Иногда пользуются понятием удельный коэффициент продуктивности Ку = К / h , т. е. коэффициент продуктивности отнесенным к единице толщины пласта. Это позволяет более объективно сопоставлять фильтрационные способности пластов в различных скважинах. Графическое изображение зависимости Q = f(Рк - Рс) или Q = f(Рc) называется индикаторной линией. Из (6.8) видно, что индикаторная линия должна быть наклонной прямой с угловым коэффициентом К. Чтобы построить индикаторную линию, необходимо иметь несколько фактических значений дебитов и соответствующие этим дебитам забойные давления Рс.

Если известно пластовое давление в скважине, то индикаторную линию можно строить в функции депрессии Р = Рк - Рс, т. е. [Q(p)]. Если пластовое давление неизвестно, то индикаторную линию строят в функции забойного давления рс, т. е. [Q(Рc)]. Экстраполируя индикаторную линию до пересечения с осью ординат, можно определить пластовое давление как ординату Р, соответствующую нулевому значению дебита (рис. 6.1). Экстраполяция индикаторной линии до пересечения с осью дебитов дает величину так называемого потенциального дебита Qпот, т. е. дебита при нулевом давлении на забое скважины. Эксплуатировать скважины при Qпот по геологическим и техническим причинам практически нельзя, за исключением скважин с обнаженным забоем, работающих в условиях гравитационного режима. Фактические точки Q(p), получаемые при исследовании скважины на нескольких установившихся режимах, обычно не ложатся точно на прямую, как на рис. 6.1, а дают разброс, иногда значительный. Кроме того, индикаторные линии не всегда получаются прямыми, как это следует из формулы притока (6.8). Искривление индикаторной линии в сторону оси давления означает увеличение фильтрационного сопротивления по сравнению со случаем фильтрации, описываемым линейным законом Дарен. Это объясняется тремя причинами.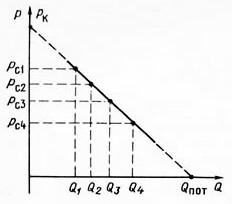



Рис. 6.1. Построение зависимости Q(Рc) по четырем фактическим точкам
1. Образованием вокруг скважины области с двухфазной фильтрацией при забойном давлении ниже давления насыщения. Чем больше эта разница, тем больше радиус области двухфазной (нефть+газ) фильтрации и, следовательно, больше фильтрационное сопротивление.

2. Изменением проницаемости и раскрытости микротрещин в породе при изменении внутрипластового давления.

3. Превышением скоростей движения жидкости в призабойной зоне критических значений, при которых линейный закон Дарси нарушается.

Искривление в сторону оси дебитов объясняется неодновременным вступлением в работу отдельных прослоев или пропластков и разными значениями в них пластовых давлений. Это можно пояснить на примере двухслойного пласта. Если пластовое давление в первом пропластке Рк1 а во втором Рк2 причем Рк1 > Рк2, то при всех забойных давлениях Рс, лежащих в пределах Рк1 > Рс > Рк2, приток будет только из первого пропластка. При снижении Рс до величины Рс < Рк2 < Рк1 будут работать оба пропластка, т. е. дебит непропорционально возрастет. Если бы в реальных скважинах процессы фильтрации были обратимы, т. е. расход при отборе был бы равен расходу при поглощении в условиях численного равенства депрессии и репрессии, то это не могло обусловить кривизну индикаторной линии, так как известно, что алгебраическая сумма линейных уравнений всегда дает результирующее линейное.

Однако по целому ряду причин процессы фильтрации необратимые, и в частности потому, что на забое всегда имеются взвесь, илистые и глинистые осадки, которые при возникновении репрессии закрывают поры, т. е. работают как обратный клапан: выпускают жидкость из пласта в скважину и задерживают в обратном направлении. Наличие многих прослоев сглаживает ход результирующей индикаторной линии, плавно загибающейся в сторону оси дебитов.

Известны многочисленные факты, когда разница в пластовых давлениях соседних пропластков, вскрываемых общим фильтром, доходила до 3 МПа, а также факты внутрипластовых перетоков. Кроме того, нелинейный характер индикаторных линий находит объяснение в аномальных неньютоновских свойствах некоторых пластовых жидкостей.

При любом виде искривления индикаторной линии ее всегда можно аппроксимировать уравнением

, (6.11)

Это уравнение называют общим уравнением притока.

При n = 1 уравнение (6.11) описывает прямолинейную индикаторную линию. При 1 > n > 1/2 - индикаторные линии с искривлением в сторону оси P, при n > 1/2 - индикаторные линии с искривлением в сторону оси Q.

Случай линейной фильтрации является аналогом ламинарному течению жидкости в трубной гидравлике. Ламинарное течение с энергетической точки зрения наиболее экономичное, поэтому в общем уравнении притока n больше единицы быть не может.

При n = 1/2 приток имеет четко выраженное турбулентное течение жидкости, когда коэффициент трения  не зависит от числа Re. Таким образом, индикаторная линия с искривлением в сторону оси дебитов (n > 1) физически невозможна. В противном случае это означало бы существование течения жидкости с энергетической точки зрения более экономичного, чем в случае ламинарного течения. Поэтому индикаторные линии с искривлением в сторону оси дебитов, когда n > 1, просто считали дефектными.

С появлением скважинных дебитомеров удалось установить истинные причины искривления индикаторных линий. При n  1 коэффициент К в общем уравнении притока теряет свой физический смысл коэффициента продуктивности и превращается просто в коэффициент пропорциональности или в угловой коэффициент.

При прямой индикаторной линии коэффициент продуктивности К может быть найден по любым двум фактическим точкам как

, (6.12)

Зная К, можно определить гидропроводность  = kh/. Для этого надо решить формулу (6.10) относительно 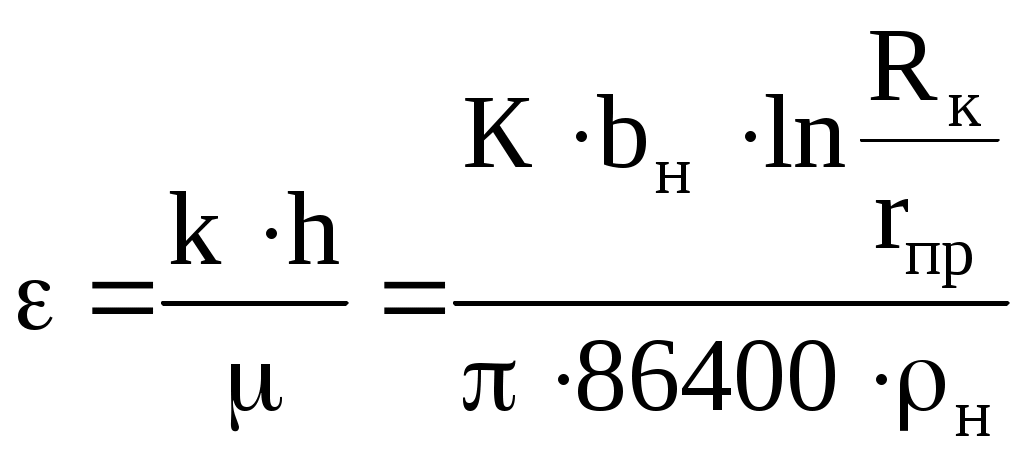

, (6.13)

Зная по геофизическим данным или по результатам глубинной дебитометрии h, а по лабораторным данным , можно определить проницаемость k в районе данной скважины. Обычно вместо Rк берут половину среднего или средневзвешенного по углу расстояния до соседних скважин. Для одиночно работающих скважин Rк принимают равным 250 - 400 м, исходя из физических представлений о процессах фильтрации.

Если имеется ряд фактических замеров дебитов Qi и соответствующих этим дебитам замеров забойного давления Pi, то по этим данным можно определить все постоянные коэффициенты общего уравнения притока. Поскольку их три (К, Pк, n), то нужно иметь по крайней мере замеры дебитов и давлений при трех режимах эксплуатации. Полагая, что индикаторная линия описывается уравнением вида (6.11), то для каждого режима будем иметь



(6.14)



Деля уравнение 1 на 2, сокращая на К и логарифмируя правую и левую часть, найдем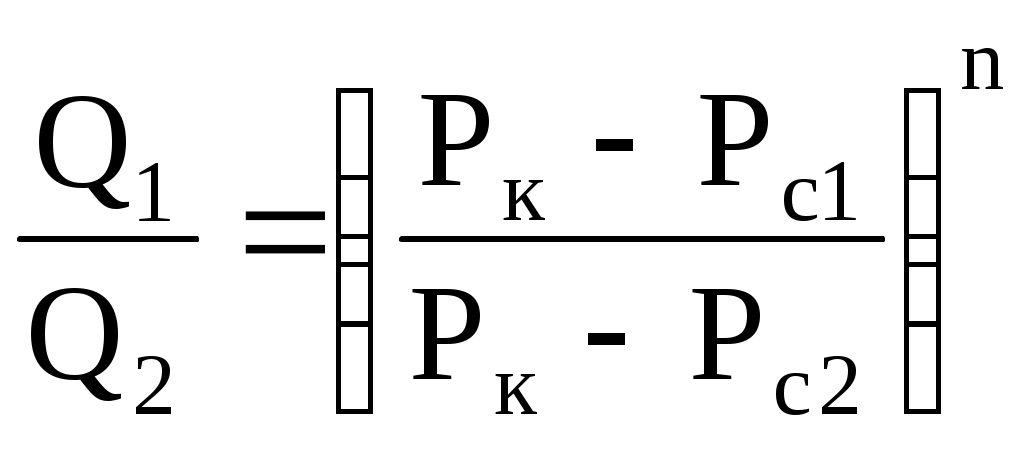



или

, (6.15)

Решая 2 с 3 аналогично, найдем

, (6.16)

Деля (6.15) на (6.16) и сокращая на n, найдем: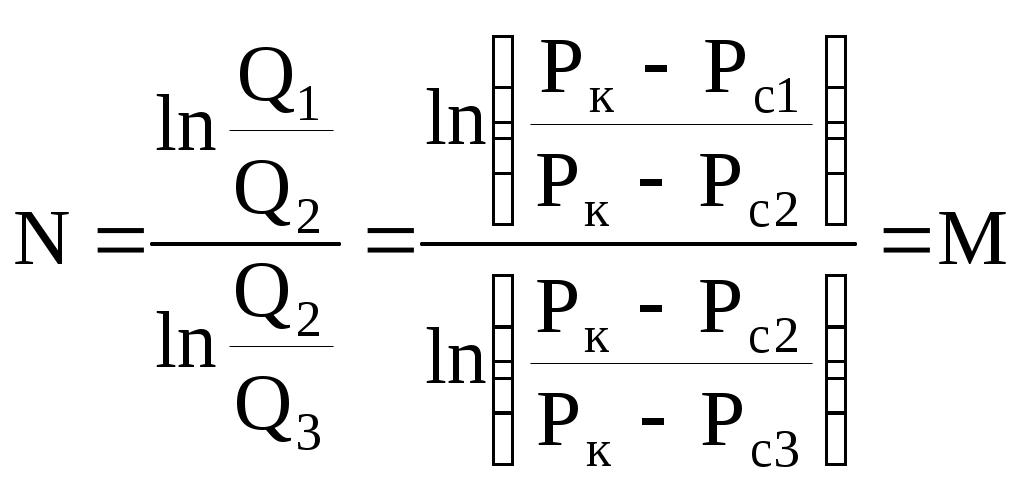

, (6.17)

Левая часть, число N, известна, так как Q₁, Q₂, Q₃ известны. Неизвестно Pк. Его аналитическое определение представляет сложности, так как уравнение (6.17) трансцендентное. Поэтому из (6.17) Pк может быть найдено графоаналитически. Задаваясь несколькими произвольными, но близкими к реальным значениям Pк, вычисляем отдельно М - правую часть равенства (6.17) и строим график зависимости М(Рк) (рис. 6.2). Находя на этом графике точку пересечения А прямой N = const с линией М(Pк), получаем абсциссу этой точки, т. е. такое значение Pк, при котором N = M. Дальнейшее определение коэффициентов К и n трудностей не представляет.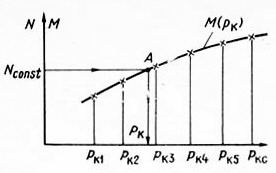



Рис. 6.2. Графоаналитический метод определениявеличины Рк.
Решая уравнение (6.15) или (6.16) относительно искомого n и подставляя в него уже найденное Pк, найдем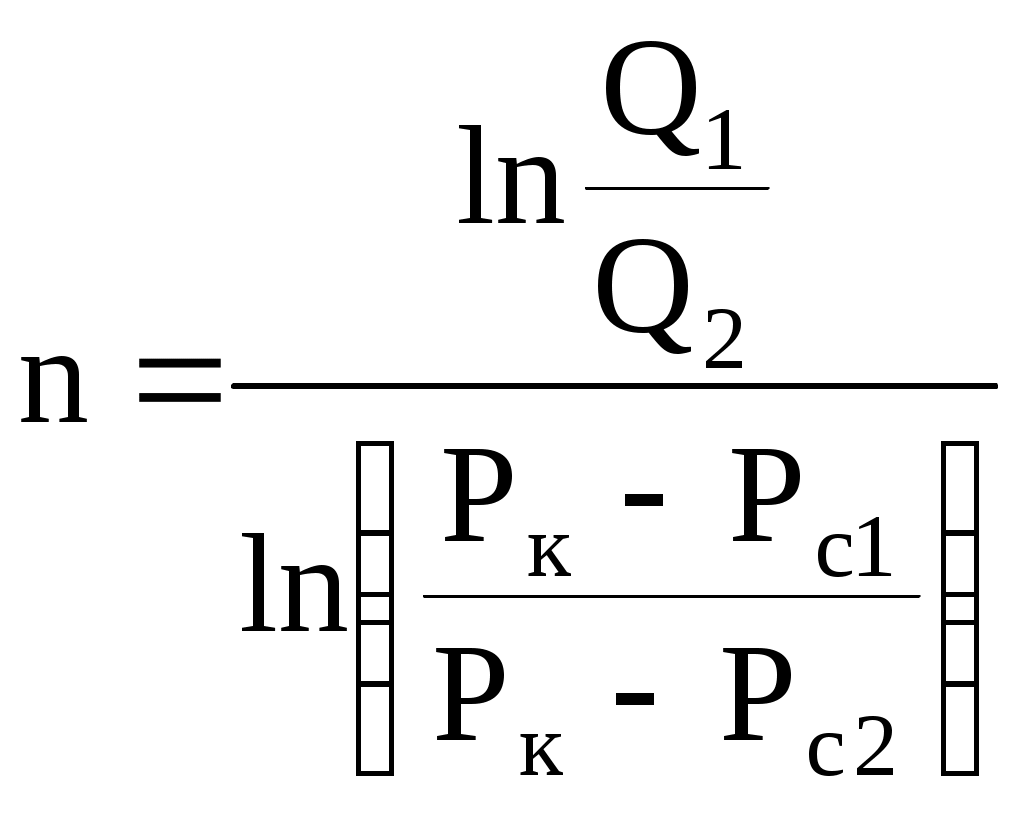

, (6.18)

И далее, из любого 1, 2, 3 уравнений, подставляя в них уже найденные Pк и n, определим К.

, (6.19)

Поскольку точки Qi и Pi всегда дают разброс, то из уравнений системы (6.14) получится три разных значения К. Рекомендуется принять среднее арифметическое.

Аналогично получится и с величиной n, из трех значений которых принимают средние арифметическое. Тогда уравнение притока в данной скважине будет

, (6.20)

Для вычисления коэффициентов К, Pк и n можно применить другие методы, например метод наименьших квадратов.

В подземной гидравлике обосновывается описание процесса фильтрации так называемой двучленной формулой

. (6.21)

По существу это есть аппроксимация индикаторной линии полиномом второй степени. При малых Q второе слагаемое в (6.21) мало. При увеличении Q оно увеличивается пропорционально квадрату Q. Уравнение (6.21) преобразуется в прямую делением всех членов на Q: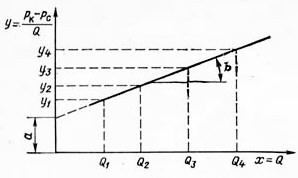

. (6.22)



Рис. 6.3. Индикаторная линия при двучленной формуле притока
Имея фактические точки, т. е. Qi, и Pci, и строя по ним график в координатах у = (Pк - Рc) / Q и x = Q, получаем прямую, не проходящую через начало координат и отсекающую на оси у отрезок a, b - угловой коэффициент этой линии (рис. 6.3):

. (6.23)

При Q  0 у = а = (Рк - Рc) / Q, откуда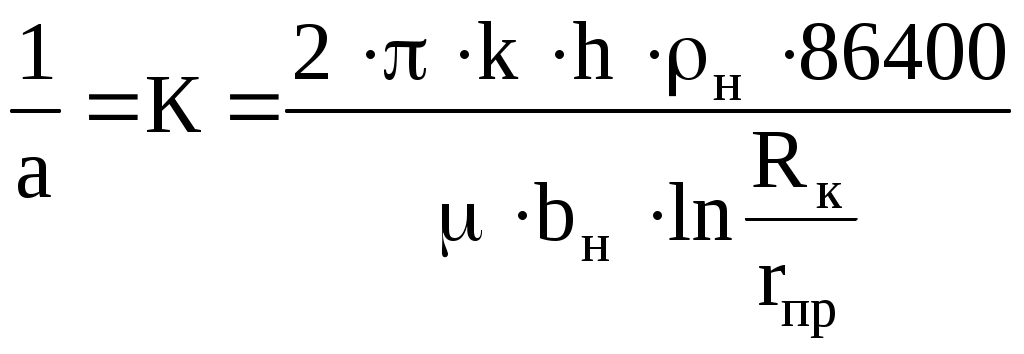

следовательно,

. (6.24)

Таким образом, в случае аппроксимации криволинейной индикаторной линии двучленной формулой необходимо по фактическим точкам перестроить индикаторную линию в координатах у = (Рк - Рc)/Q, х = Q, определить отрезок а и далее согласно формуле (6.24) найти искомые параметры: гидропроводность  или проницаемость k. В случае фильтрации в пласте газированной жидкости, т. е. при Рпл < Рнас, параметры пласта определяют по формуле установившегося радиального притока газированной жидкости, которая решается относительно искомой .

Формула имеет вид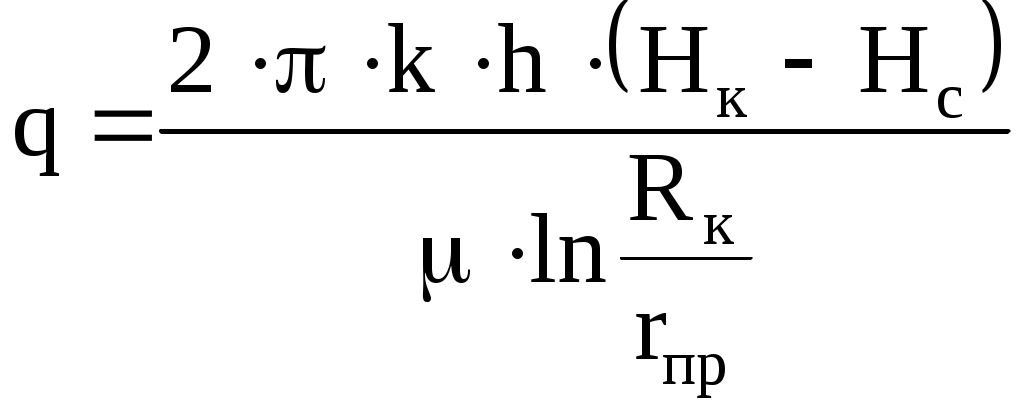

, (6.25)

где Нк и Нс - функции, учитывающие изменение газонефтенасыщенности и фазовой проницаемости для жидкости при изменении давления. Остальные обозначения прежние.

Физически величина (Нк - Нс) представляет собой ту часть общей депрессии, которая необходима для проталкивания к забою скважины только жидкости.

Функция Н через известные забойные давления вычисляется с помощью специальных аппроксимирующих формул, различных для различных интервалов давлений. Обычно методы определения параметров пласта при установившихся отборах газированной жидкости описываются в соответствующих инструкциях, как правило, не отличаются надежностью и применяются редко.

В заключение необходимо заметить, что использование формул установившегося радиального притока для определения гидропроводности пласта  = kh/ дает значения этого параметра, характерные для призабойной зоны пласта, так как в этой зоне происходит наибольшее падение давления.