Курсовая газы. сравнительный анализ установившихся потоков газа при различных законах фильтрации
 Скачать 326.86 Kb. Скачать 326.86 Kb.
|
|
Министерство науки и высшего образования Российской Федерации федеральное государственное бюджетное образовательное учреждение высшего образования «Сахалинский государственный университет» Технический нефтегазовый институт Кафедра геологии и нефтегазового дела
КУРСОВАЯ РАБОТА по дисциплине «ПОДЗЕМНАЯ ГИДРОМЕХАНИКА» на тему: «СРАВНИТЕЛЬНЫЙ АНАЛИЗ УСТАНОВИВШИХСЯ ПОТОКОВ ГАЗА ПРИ РАЗЛИЧНЫХ ЗАКОНАХ ФИЛЬТРАЦИИ»
Южно-Сахалинск 2020 Министерство науки и высшего образования Российской Федерации федеральное государственное бюджетное образовательное учреждение высшего образования «Сахалинский государственный университет» Технический нефтегазовый институт Кафедра геологии и нефтегазового дела ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ По дисциплине «ПОДЗЕМГАЯ ГИДРОМЕХАНИКА» Студенту Левун И.А. группы: НДз-17/02 1.Тема «СРАВНИТЕЛЬНЫЙ АНАЛИЗ УСТАНОВИВШИХСЯ ПОТОКОВ ГАЗА ПРИ РАЗЛИЧНЫХ ЗАКОНАХ ФИЛЬТРАЦИИ» Утверждена на заседании кафедры протокол № ______ от «__»__________ 20__ года. 2. Срок сдачи студентом законченной работы «__» _____20__ года. 3. Исходные данные к работе: Давление на контуре питания,  , ,  =0,015 =0,015  , ,  = = 4. Содержание работы: Основные понятия теории фильтрации. Линейный закон фильтрации Дарси. Плоскорадиальный фильтрационный поток газа по двухчленному закону фильтрации. Плоскорадиальный фильтрационный поток газа по степенному закону фильтрации. Примеры решения задач по теории фильтрации. Практическое использование законов фильтрации. 5. Перечень графического материала: 6. Руководитель: Резвых В.А., доцент кафедры геологии и нефтегазового дела дата и подпись руководителя Задание принял к исполнению дата и подпись студента СОДЕРЖАНИЕ «ПОДЗЕМНАЯ ГИДРОМЕХАНИКА» 1 «СРАВНИТЕЛЬНЫЙ АНАЛИЗ УСТАНОВИВШИХСЯ ПОТОКОВ ГАЗА ПРИ РАЗЛИЧНЫХ ЗАКОНАХ ФИЛЬТРАЦИИ» 1 ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ 2 По дисциплине «ПОДЗЕМГАЯ ГИДРОМЕХАНИКА» 2 Студенту Левун И.А. группы: НДз-17/02 2 ВВЕДЕНИЕ 5 1 ТЕОРЕИТИЧЕСКИЕ ОСНОВЫ ЗАКОНОВ ФИЛЬТРАЦИИ УСТАНОВИВШИХСЯ ПОТОКОВ ГАЗА 7 1.1 Основные понятия теории фильтрации 7 1.2 Линейный закон фильтрации Дарси 10 1.3 Плоскорадиальный фильтрационный поток газа по двухчленному закону фильтрации 14 1.4 Плоскорадиальный фильтрационный поток газа по степенному закону фильтрации 20 2 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕОРИИ ФИЛЬТРАЦИИ 23 2.1 Задача 1 23 2.2 Задача 2 23 2.3 Задача 3 25 2.4 Задача 4 (по исходным данным) 26 3 ПРАКТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ ЗАКОНОВ ФИЛЬТРАЦИИ 30 ЗАКЛЮЧЕНИЕ 33 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 34 ВВЕДЕНИЕ 4 1 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЗАКОНОВ ФИЛЬТРАЦИИ УСТАНОВИВШИХСЯ ПОТОКОВ ГАЗА 6 1.1 Основные понятия теории фильтрации 6 1.2 Линейный закон фильтрации Дарси 9 1.3 Плоскорадиальный фильтрационный поток газа по двухчленному закону фильтрации 13 1.4 Плоскорадиальный фильтрационный поток газа по степенному закону фильтрации 19 2 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕОРИИ ФИЛЬТРАЦИИ 22 2.1 Задача 1 22 2.2 Задача 2 22 2.3 Задача 3 24 2.4 Задача 4 (по исходным данным) 25 3 ПРАКТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ ЗАКОНОВ ФИЛЬТРАЦИИ 29 ЗАКЛЮЧЕНИЕ 32 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 33 ВВЕДЕНИЕАктуальность курсовой работы определяется тем, что подземная гидромеханика – наука, изучающая законы течения природных жидкостей-нефти, воды и газа в пористой среде – теоретическая основа для разработки нефтегазовых месторождений, одна из профилирующих дисциплин в учебном плане нефтяных университетов. Подземная гидромеханика является основой современной технологии для добычи нефти и добычи газа и имеет обширные области [5]. Цель работы: произвести сравнительный анализ установившихся потоков газа при различных законах фильтрации. Задачи курсовой работы: изучить теоретические основы законов фильтрации установившихся потоков газа; охарактеризовать основные понятия теории фильтрации; анализировать линейный закон фильтрации Дарси; определить плоскорадиальный фильтрационный поток газа по двухчленному закону фильтрации; рассмотреть плоскорадиальный фильтрационный поток газа по степенному закону фильтрации; произвести решение задач по теории фильтрации; определить практическое использование законов фильтрации. Для решения поставленных задач использовались следующие методы: теоретический анализ, сравнение, систематизация, классификация, формализация, абстрагирование, описание, практический анализ и обобщение. Объект исследования: законы фильтрации. Предмет исследования: состояние установившихся потоков газа при различных законах фильтрации. Структура курсовой работы: работа состоит из введения, трёх глав, разбитых на пункты, заключения, списка использованных источников. Во введении прослеживается актуальность выбранной темы, ставятся цели и задачи работы, определяется объект и предмет исследования. В первой главе изучаются общие об основах законов фильтрации установившихся потоков газа. Во второй главе происходит решение задач, непосредственно которые связаны с темой работы. В третьей главе представляется роль практического использования законов фильтрации. В заключении подводится итог проделанной курсовой работы. Текст курсовой работы изложен на 34 страницах, в том числе содержит 3 таблицы, 11 рисунков и 16 наименований, содержавшиеся в списке использованной литературы. Таким образом, определив цель и задачи курсовой работы, можно приступать к решению поставленных задач. 1 ТЕОРЕИТИЧЕСКИЕ ОСНОВЫ ЗАКОНОВ ФИЛЬТРАЦИИ УСТАНОВИВШИХСЯ ПОТОКОВ ГАЗА1.1 Основные понятия теории фильтрацииФильтрацией называют движение газов, жидкостей, а также их смесей в пористых средах, то есть в твердых телах, которые пронизаны системой микротрещин, которые сообщаются между собой. Если говорить о фильтрации жидкостей и газов, то по сравнению с движениям по трубам и каналам она имеет определенные особенности. Так, например, фильтрация может проходить по норовым каналам даже при малой скорости движения жидкости. При это силы трения во время движения жидкости очень велики, ведь площадь соприкосновения жидкости и твердыми частицами имеет внушительную величину [3]. Пористую среду можно характеризовать коэффициентами пористости просветности. Коэффициент пористости есть отношение объема пор (τпор) ко всему объему пористой среды:  (1) (1)При этом, в теории фильтрации под пористостью можно понимать активную пористость, учитывающую те микротрещины, которые между собой соединяются и через которые фильтруется жидкость. Коэффициентом просветности П является отношение площади просветов (ωпросв) в данном сечении пористой среды ко всей площади этого сечения (ω). 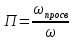 (2) (2)Таким образом можно сказать, что среднее значение проссветности по длине пласта равно пористости, что можно увидеть в формуле.  (3) (3)Итак, среднее значение площади просветов выглядит так:  (4) (4)Более простой моделью пористой среды можно назвать модель фиктивного грунта, который состоит из шариков, имеющих одинаковый диаметр, при этом, уложенных определенным образом. В зависимости от острого угла θ боковой грани ромбоэдра укладка шаров более или менее плотная [3]. Этот угол можно изменяться в пределах от 60 до 90 градусов, при этом если θ = 60°, то наблюдается плотная укладка шаров, θ = 90° - свободная. Увидеть фиктивный грунт можно на рисунке 1.  Рисунок 1 – Модель фиктивного грунта Пористость фиктивного грунта можно определить, используя формула Слихтера.  (5) (5)Из данной формулы следует то, что сама пористость не зависит от диаметра частиц, влияет на нее их взаимное расположение, определяемое углом θ. Для того, что использовать формулы на реальном грунте, то его стоит заменить аналогичным фиктивным. Главное, он должен иметь такое же гидравлическое сопротивление. Диаметр частиц фиктивного грунта называют эффективным диаметром d3. Его можно определить при помощи механического анализа, необходимо просеять его через сооружение, имеющее различную площадь отверстий, разделив его на фракции. Средним диаметром станет среднее арифметическое. 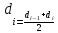 (6) (6)Затем строят кривую механического (фракционного) состава грунта, откладывая по оси абсцисс средние диаметры фракций di а но оси ординат –сумму масс фракций 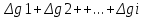 в % от общей массы. в % от общей массы.Последняя точка кривой имеет абсциссу, равную dn, и ординату  . .Данную ось можно увидеть на рисунке 2. 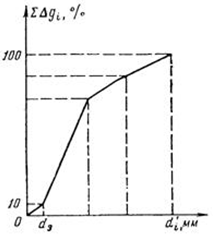 Рисунок 2 – Кривая фракционного состава грунта Существует много способов определения эффективного диаметра. По способу А. Газена dэ определяется по кривой механического состава. За эффективный принимается такой диаметр шарообразной частицы, который соответствует сумме масс всех фракций, начиная от нуля и кончая этим диаметром, равной 10%. Надо найти, кроме того, диаметр d0, который соответствует сумме масс фракций равной 60%. Коэффициент однородности do/dэдолжен быть не более 5 (do/dэ ≤ 5) и dэдолжен лежать в пределах от 0,1 до 3 мм [2, 3]. По способу Крюгера – Цункера используют данные механического анализа грунта и определяют dэпо формуле:  (7) (7)Скоростью фильтрации w называется отношение объемного расхода жидкости к площади поперечного сечения пласта, нормального к направлению движения жидкости. 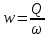 (8) (8)При этом, средняя скорость движения жидкости v равна отношению объемного расхода к площади просветов 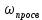 (живому сечению потока). (живому сечению потока). (9) (9)Как итог, скорость фильтрации будет равна: 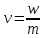 (10) (10)1.2 Линейный закон фильтрации ДарсиЗакон Дарси – закон фильтрации жидкостей и газов в пористой среде. Он устанавливает линейную зависимость между объемным расходом жидкости или газа и гидравлическим градиентом (уклоном, перепадом давления) в пористых средах, например, в мелкозернистых, песчаных и глинистых грунтах [1]. Основная формула:  (11) (11)Данный закон также может быть записан следующей формулой: 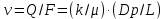 (12) (12)где Q – объемный расход жидкости, F – площадь поперечного сечения образца или эффективная площадь рассматриваемого объема пористой среды, v – скорость фильтрации жидкости или газа, k – коэффициент проницаемости среды, p1 и p2 – давления, созданные на концах испытуемого образца, Dр – перепад давления на длине среды L, μ – абсолютная вязкость жидкости, L – длина фильтрующей части породы. Его обычно используют для расчетов режима разработки нефти и газа. В данной формуле коэффициентом k является коэффициент фильтрации, который характеризует среду и жидкость одновременно. Все зависит от размеров самих частиц, а также от их формы и степени шероховатости. Для того, чтобы реализовать в жизни закон Дарси, необходимо рассмотреть лабораторную установку, которая предназначена для изучения пористых сред. Данная установка изображена на рисунке 3 [1, 4].  Рисунок 3 – Лабораторная установка для изучения пористых сред Обозначения: баллон с газом (для жидкости – насос); вентиль; регулятор давления; входной манометр; модель (пористая среда); выходной манометр; расходомер. При помощи регулятора давления лаборанты подбирают значения перепада по длине модели. При этом должен выполняться линейный закон Дарси. Данный закон используется в системах очистки жидкостей и газов. Например, на его основе работают многие противогазы. Закон Дарси справедлив в большинстве случаев, об этом свидетельствуют многие данные, но его можно и нарушить, поэтому существует верхний и нижний предел его применения. В первом случае мы имеем в виду применимость линейного закона фильтрации к движению подземных вод преимущественно в карстовых породах и породах с крупными системами открытых трещин, а во втором – движение воды в глинистых мелкодисперсных породах. При высоких скоростях возникают инерционно-пульсационные силы, которые имеют квадратичную зависимость от скорости потока, а при движении в мелкодисперсных породах возникают силы взаимодействия молекул, которые структурируют жидкость и тем самым усиливают тормозящий эффект сил внутреннего сопротивления [1, 2]. Увидеть график обобщенного закона Дарси можно на рисунке 4. 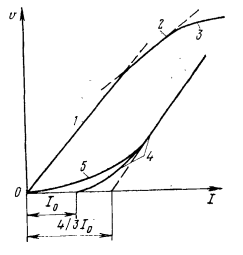 Рисунок 4 – Обобщенный график закона Дарси где, графики: линейного закона Дарси; приближенной линейной зависимости для переходного режима фильтрации, обобщенного закона при линейно-турбулентном режиме фильтрации; то же, при линейно-вязкопластическом движении; 5-то же, с учетом молекулярного взаимодействия. Отклонения от линейного закона в основном связаны с высокими значениями градиентов давления и участками резкого увеличения стока подземных вод, что редко в естественных гидрогеологических условиях и может наблюдаться на локальных участках вблизи инженерных сооружений, например, в районе плотины со значительным повышением уровня воды, вблизи водяных скважин при откачке высокопроницаемых отложений со значительными перепадами уровня воды в этих скважинах и так далее. Каждый такой случай требует особого обоснования [6]. Основываясь на принципе независимости действия сил вязкого трения и инерционно-пульсационных сил, Р. Прони предложил обобщенную форму основного закона фильтрации в виде двухчленной связи, которую Ф. Форххаймер использовал в 1895 г. Первый член данной связи характеризует ламинарное течение, а второй – течение, в котором проявляются инерционно-пульсационные силы. В работе В.М. Шестакова предложены более удобные обозначения:  (13) (13)K – коэффициент фильтрации в ламинарном режиме,  – коэффициент нелинейности фильтрации. – коэффициент нелинейности фильтрации.Параметр нелинейности можно определить следующим выражением:  (14) (14)1.3 Плоскорадиальный фильтрационный поток газа по двухчленному закону фильтрацииДвучленный закон для плоскорадиальной фильтрации имеет следующую формулу:  (15) (15)Также можно выразить через массовый расход:  (16) (16)Если подставить в первую формулу, то получается:  (17) (17)Применим функцию Лейбензона:  (18) (18)Если разделить переменные и ввести функцию Лейбензона, то получается: 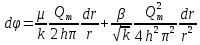 (19) (19)Интегрируя последнее уравнение в пределах от rс до Rк, от Рс до Рк получим:  + + (20) (20)Переходя от функции Лейбензона к давлению по формуле  (21) (21)Для совершенного газа можно найти уравнение притока к скважине:  (22) (22)В данном случае 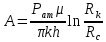 (23) (23)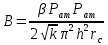 (24) (24)А и В являются коэффициентами фильтрационных сопротивлений, они постоянны для скважины. Их можно определить только опытным путем по данным исследования скважины при установившихся режимах. Уравнение притока реального газа к скважине по двучленному закону фильтрации имеет вид:  (25) (25)Схему притока газа к несовершенной по степени и характеру вскрытия скважине можно увидеть на рисунке 5.  Рисунок 5 – Схема притока газа к несовершенной по степени и характеру вскрытия скважине Если скважины несовершенна, то коэффициенты A и B будут иметь следующий вид:  (26) (26)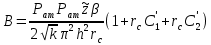 (27) (27)где  являются коэффициентами, которые характеризуют несовершенные скважины до степени вскрытия. являются коэффициентами, которые характеризуют несовершенные скважины до степени вскрытия.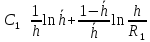 (28) (28) , ,  = = (29) (29)Обе последние формулы – приближенные, они имеют место при значениях b>R1.  и и 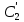 характеризуют несовершенство скважины по характеру вскрытия. характеризуют несовершенство скважины по характеру вскрытия.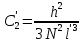 (30) (30)где N – суммарное число перфорационных отверстий, 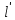 – глубина проникновения перфорационной пули в пласт. – глубина проникновения перфорационной пули в пласт.Технология исследований «Исследование газовых скважин в стабильных условиях» проводится в следующем порядке [16]: Перед испытанием колодец продувают 15-20 минут. Для удаления твердых частиц и жидкости со дна колодцев. После продувки скважину закрывают до полного восстановления давления. На многих газовых месторождениях это время составляет 2-3 часа. В мембранном измерителе критического расхода газа (ДИКТ) установлена диафрагма с малым диаметром калиброванного отверстия. Открывается основной клапан, скважина вводится в работу до достижения стабильного состояния, при котором давление и температура газа перед диафрагмой ДИКТ и в кольце не меняются с течением времени. Записывают эти значения давления и температуры газа, после чего скважину закрывают как показано на рисунке 6. В дикт устанавливается диафрагма с большим диаметром калиброванного отверстия и регистрируют давление и температуру, после чего скважина останавливается. Расход газа для каждой мембраны рассчитывается по давлению и температуре газа под мембраной. На основании статического кольцевого давления или динамического давления перед мембраной ДИКТ рассчитывается давление на забое скважины.   Рисунок 6 – Схема расположения оборудования и приборов при испытании диафрагменным измерителем критического течения где: 1 – диафрагменный измеритель, 2 – породоуловитель, 3 – 6 – манометры. Обработка результатов исследований скважин начинается с определения давления на забое. Наиболее достоверные данные получаются при прямом измерении забойных давлений с помощью бурового инструмента. Однако, если газ достаточно чистый (примеси не превышают 1-10 г / см3), вполне допустимо определять давление на забое скважины по давлению в устье. Со стационарной газовой колонкой [14, 16]: 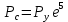 (31) (31)где  – давление на забое, – давление на забое, - давление на неподвижном столбе на устье. - давление на неподвижном столбе на устье. (32) (32)где 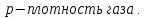 H – глубина до расчетного уровня, м. z – среднее по высоте значение коэффициента сжимаемости газа; T – средняя по скважине абсолютная температура газа, К. Если в скважине не образуется неподвижный столб газа и давление не получается замерить, то забойное давление рассчитывается так:  (33) (33)где Pc и Py – абсолютное давление на забое и устье, q – расход газа.  (34) (34)где 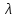 можно определить по справочникам как функцию числа Рейнлодьса, относящаяся к шероховатости труб. Средний диапазон колеблется от 0,014 до 0,025. можно определить по справочникам как функцию числа Рейнлодьса, относящаяся к шероховатости труб. Средний диапазон колеблется от 0,014 до 0,025.Zcp – определяется по значениям Р и Т на устье скважины и по предполагаемым их значениям на забое; d – внутренний диаметр фонтанных труб, м. При движении газа по кольцевому пространству в формуле следует использовать эквивалентный диаметр, который можно определить из условия равенства площади кольцевого сечения труб площади эквивалентного круга: 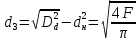 (35) (35)где 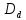 – внутренний диаметр внешней трубы, – внутренний диаметр внешней трубы, – наружний диаметр внутренней трубы, – наружний диаметр внутренней трубы,F – площадь сечения. Когда газ движется по кольцевому сечению, то изменяется и 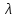 . Газ из скважины выходит с капельной жидкость, значения . Газ из скважины выходит с капельной жидкость, значения 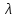 составляют 0,018-0,014. составляют 0,018-0,014.После того, как давления были определены, необходимо рассчитать расходы газа. Это определяется с помощью диафрагменного измерителя критического течения, который можно увидеть на рисунке 7 [16]. 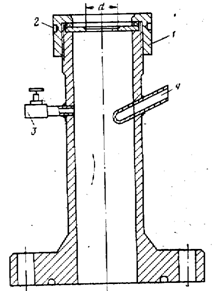 Рисунок 7 – Диафрагменный измеритель критического течения Формула расхода газа: 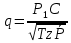 (36) (36)где 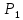 – давление до диафрагмы, МПа; – давление до диафрагмы, МПа; – коэффициент расхода зависящий от диаметра и формы диафрагмы – коэффициент расхода зависящий от диаметра и формы диафрагмыP – относительная плотность газа; T – абсолютная температура газа до диафрагмы; z – коэффициент сжимаемости газа. 1.4 Плоскорадиальный фильтрационный поток газа по степенному закону фильтрацииНеобходимо спроектировать степенной закон фильтрации на цилиндрическую систему координат для плоскорадиального фильтрационного потока. Получается следующая формула:  (37) (37)Сама математическая модель, кроме закона фильтрации, содержит в себе уравнение неразрывности. Интегрирование уравнения неразрывности в результате приводит к виду [14]:  (38) (38)Выражение массового расхода будет иметь вид:  (39) (39)Для того, чтобы проинтегрировать уравнение, необходимо его возвести в степень n.  (40) (40)Можно преобразовать к виду: 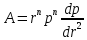 (41) (41) (42) (42)Необходимо разделить переменные: 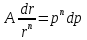 (43) (43)Функция давления P’:  (44) (44)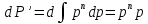 (45) (45)Таким образом, уравнение можно переписать следующим образом:  (46) (46)После интегрирования от забоя до контура питания, т.е. используя для интегрирования уравнения граничные условия:  Получается:  (47) (47)Если подставить вместо A представление через параметры пласта и фильтрационных потоков, то получится следующее:  (48) (48)Формула для дебита  (49) (49)Если в равенстве в качестве нижнего предела интегрирования принять произвольную точку, то получается формула для распределения в пласте функции давления:  (50) (50)Функция давления для несжимаемой жидкости:  (51) (51)Для совершенного газа:  (52) (52)Из формулы для дебита получается формула для скорости фильтрации. Рассмотрим все расчетные формулы для плоскорадиальной фильтрации по степенному закону для несжимаемой жидкости [11, 12]. Формула массового дебита: 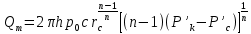 (53) (53)Формула для объемного дебита:  (54) (54)Формула для распределения давления в пласте:  (55) (55)Формула для скорости фильтрации:  (56) (56)2 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕОРИИ ФИЛЬТРАЦИИ2.1 Задача 1Необходимо показать, что пористость m, а также просветность п фиктивного грунта никак не зависят от частиц, слагающих грунт. Угол грани ромбоэдра 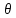 = 90°. Ромбоэдр изображен на рисунке 8 [4]. = 90°. Ромбоэдр изображен на рисунке 8 [4]. Рисунок 8 – Ромбоэдр Для решения необходимо рассмотреть основную ячейку фиктивного грунта по Слихтеру. Пористость элемента:  (57) (57)Таким образом, пористость не зависит от диаметра. Для просветности:  (58) (58)2.2 Задача 2Пласт имеет установившуюся плоскорадиальную фильтрацию газированной нефти [4, 8]. Необходимо выяснить, в каком случае при депрессии  и газовом факторе Г = 200 м3/ и газовом факторе Г = 200 м3/ будет наблюдаться самый высокий дебит, с учетом того, что пластовые давления различаются. будет наблюдаться самый высокий дебит, с учетом того, что пластовые давления различаются.1) pк = 9,8 МПа (100 кгс/см2); 2) рк = 4,9 МПа (50 кгс/см2). Коэффициенты вязкости нефти н = 1 мПас и газа r = 0,012 мПас, коэффициент растворимости газа в нефти S= 1,7310-5 м3/м3Па. Решением будет следующим  Следующей задачей станет сравнить дебиты при установившейся плоскорадиальной фильтрации газированной нефти по закону Дарси при рядных газовых факторах и одной и той же депрессии. Отношение ж/г = 100, коэффициент растворимости газа в нефти S = 1,0210-5 м3/м3Па, рат = 9,8104 Па, давление на контуре литания рк = 11,76 МПа (120 кгс/см2), давление на забое скважины рс = 9,8 МПа (100 кгс/см2). Газовые факторы Г1 = 300 м3/м3 и Г2 = 600 м3/м3. Пласт представлен несцементированным песком [4]. Решение будет следующим:   Итак, при равных условиях, а также неизменяющейся депрессии с повышением газового фактора дебит жидкой фазы уменьшается, а газовой – возрастает. 2.3 Задача 3Необходимо показать, что при прямолинейно-параллельном установившемся движении газа в пористой среде в условиях напорного режима распределение давления в пласте не описывается законом фильтрации в виде одночленной формулы [7]. Учитывая принцип однородности размерностей:  (59) (59)где X – координата, которая взята вдоль линии тока по движению газа. Массовый расход будет следующим:  (60) (60)Обозначим: 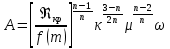 (61) (61)Введем функцию Лейбензона:  (62) (62)Получается уравнение:  Следовательно  Необходимо проинтегрировать уравнение с учетом граничных условий где   Получается:  Итог:  Если интегрировать по x от 0 до x, по Р от Рк до Р, получается:    Если перейти от функции Лейбензона к давлению, то получается закон распределения давления:  Он не зависит от значения, которое характеризует закон фильтрации. 2.4 Задача 4 (по исходным данным)В пласте происходит фильтрация прямолинейно-параллельного установившегося потока по закону Дарси совершенного газа. Построить графики зависимости распределения давления, градиента давления и скорости фильтрации от координаты x. Дано:  , ,  =0,015 =0,015  , ,  = = . .Распределение давления совершенного газа:  (63) (63)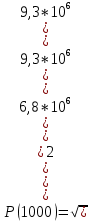 Таблица 1 – Распределение давления совершенного газа
Градиент давления совершенного газа:  (64) (64) Таблица 2 – Градиент давления совершенного газа
Скорость фильтрации совершенного газа:  (65) (65)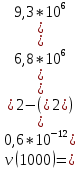 Таблица 3 – Скорость фильтрации совершенного газа
 Рисунок 9 – График зависимости распределения давления от координаты x  Рисунок 10 – График зависимости градиента давления от координаты x  Рисунок 11 – График зависимости скорости от координаты x 3 ПРАКТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ ЗАКОНОВ ФИЛЬТРАЦИИЗаконы фильтрации, которые были рассмотрены в данной работе, широко используются в подземной гидромеханике. Установившимся фильтрационным потоком можно назвать такой поток, чьи фильтрационные характеристики являются постоянными во времени. То есть, с течением времени никак не изменяются [9, 13]: распределение давления, распределение градиента давления, скорость фильтрации, массовый расход. Одномерные фильтрационные потоки – потоки, давление в которых является функцией одной координаты. В работе было рассмотрено два вида потока: прямолинейный и плоскорадиальный. Траектории потоков в пространстве могут быть представлены как фильтры, которые состоят из одномерных фильтрационных потоков. При этом прямолинейно-параллельный поток наблюдается на некоторых участков пластов залежей газа при движении жидкостей в направлении от нагнетательных скважин к эксплутационным, такие пласты носят название полообразных. При этом их толщина имеет постоянную величину, а граничный контур непроницаем, как непроницаемы кровля и подошва пластов [1, 10]. Параллельно начальному контуру расположена батарея эксплуатационных скважин. Чем меньше расстояние между скважинами, тем больше приближение, причем если заменить батарею галерей (сплошной прямолинейной выработкой), то движение газов к галерее будет параллельным по прямой траектории. Плоскорадиальные потоки часто используются в практике, потому что приток газа к забоям эксплуатационных гидродинамически совершенных скважин можно отнести к законам плоскорадиальной фильтрации. Причем поток для эксплуатационной скважины будет радиально-сходящим, а для нагнетательной – радиально-расходящим. Плоскорадиальный поток заполняет всю скважину, от стенки до контура питания. Рядом с гидродинамически-несовершенной скважиной линия тока искривляется, поэтому поток будет являться плоскорадиальным при удалении от скважины на небольшое расстояние [14]. Радиально-сферический поток реализуется в том случае, когда скважины вскрывает плоскую горизонтальную кровлю пласта, при этом продуктивные пласты газовых месторождений имеет неоднородное строение, наблюдается непроницаемость кровли. Сам пласт должен иметь неограниченную толщину, а забой полусферическую форму. Приближение к данному виду потока тем лучше, чем глубина вскрытия меньше толщины пласта. Бывает два вида неоднородности: слоистая – пласт сложен пропластками разной проницаемости, зональная – по площади и по простиранию пласта. При разработке газового месторождения, важной является задача о притоке жидкости к скважине при наличии вокруг забоя кольцевой зоны, имеющей проницаемость, которая отличается от других частей пласта. Другими словами, слой состоит из двух различных зон, имеющих разную проницаемость. Такая задача может возникать в следующих случаях: торпедирование, кислотная обработка призабойной зоны, вынос мелких фракций породы из зоны, установка гравийных фильтров, глинизация, парафинизация призабойной зоны. Необходимо устанавливать влияние на продуктивность скважины различия проницаемостей кольцевой призабойной зоны, а также других частей пласта. Виды одномерных потоков, которые были описаны в работе играют важную роль при решении задач нефтегазовой практики. Они являются основой для исследований различных закономерностей течения жидкости в пласте в зависимости от принятой системы разработки и от конструкций самих скважин. Если смоделировать один из видов одномерных потоков, то можно увидеть определенную схематизацию реальных пластов и течения жидкости. Но данных схемы не только приближенно воспроизводят случаи течения жидкости, но и помогают в изучении сложные виды потоков пластовой жидкостей в случаях, когда фильтрационный поток можно представить состоящим из простейших видов потока. ЗАКЛЮЧЕНИЕВ курсовой работе были рассмотрены фильтрационные потоки газа при различных законах фильтрации: линейный закон фильтрации Дарси; плоскорадиальный фильтрационный поток газа по двухчленному закону фильтрации; плоскорадиальный фильтрационный поток газа по степенному закону фильтрации; Фильтрацией называют движение газов, жидкостей, а также их смесей в пористых средах, то есть в твердых телах, которые пронизаны системой микротрещин, которые сообщаются между собой. Если говорить о фильтрации жидкостей и газов, то по сравнению с движениям по трубам и каналам она имеет определенные особенности. Так, например, фильтрация может проходить по норовым каналам даже при малой скорости движения жидкости. При это силы трения во время движения жидкости очень велики, ведь площадь соприкосновения жидкости и твердыми частицами имеет внушительную величину. Во второй главе курсовой работы были рассмотрены несколько задач, которые являются примером для решения вопросов на тему фильтрационных потоков газа. Закон фильтрации газов представляет большой теоритический и практический интерес, так как без знаний в этой области невозможно рассчитать дебиты газа, условия их изменения во времени при различных условиях, а также нет возможности определить основные параметры пласта. Поэтому данные законы постоянно используются во время исследования и монтажа газовых скважин. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВБасниев Н.М. Подземная гидромеханика. // Н.М. Дмитриев, Г.Д. Розенберг. – М. 2005. Бубнов В.А. Гидродинамика: Механика частицы жидкости. - М.: Ленанд, 2018. - 304 c. Евдокимова В.А. Учебное пособие для вузов. // И. Н. Кочина. - Издание второе, стереотипное, 1979. Кравченко М.Н. Фонд: Учебно-методические пособия. // Разбегина Е.Г. 2003. Леонтьев Н.Е. Основы теории фильтрации, 2009. Павлов Г.А. Нелинейная теория отклика и гидродинамика плотных сред с источниками // Г.А. Павлов, Ю.В. Трощиев. - М.: Ленанд, 2019. - 152 c. Павловский В.А. Вычислительная гидродинамика. Теоретические основы: Учебное пособие // В.А. Павловский, Д.В. Никущенко. - СПб.: Лань, 2018. - 368 c. Петров А.Г. Аналитическая гидродинамика: Идеальная несжимаемая жидкость. - М.: Ленанд, 2017. - 368 c. Петров А.Г. Аналитическая гидродинамика. - М.: Физматлит, 2010. - 520 c. Салов Н.Н. Уменьшение температурных напряжений в дисках: Монография // А.А. Харченко. - М.: Вузовский учебник, 2015. - 384 c. Серия «Современные нефтегазовые технологии» К.С Басниев 2005, 543 с. Тимофеева А.С. Гидродинамика двухфазных систем: Учебное пособие. - Ст. Оскол: ТНТ, 2012. - 264 c. Тишин В.Б. Культивирование микроорганизмов: кинетика, гидродинамика, тепломассообмен. - СПб.: Профессия, 2011. - 184 c. Тишин В.Б. Культивирование микроорганизмов: кинетика, гидродинамика, тепломассообмен. - М.: Профессия, 2012. - 184 c. Шиляев, М.И. Гидродинамика и тепломассообмен пленочных течений в полях массовых сил и их приложения: Монография / М.И. Шиляев, А.В. Толстых. - М.: Инфра-М, 2016. - 224 c. Чарный И.А. Подземная гидрогазодинамика. Госкомтехиздат, Москва, 1963, - 284 с. |

 , Па/м
, Па/м