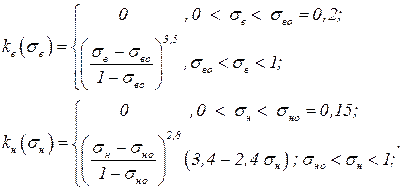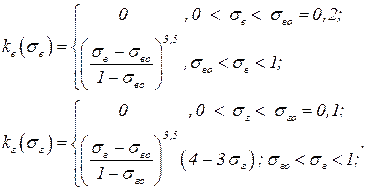Закон Дарси. Закон Дарси (Анри Дарси, 1856) закон фильтрации жидкостей и газов в пористой среде. Исторически закон был получен А. Дарси экспериментально1, но может быть получен с помощью осреднения уравнений Навье Стокса,

• Название: Закон Дарси (Анри Дарси, 1856) закон фильтрации жидкостей и газов в пористой среде. Исторически закон был получен А. Дарси экспериментально1, но может быть получен с помощью осреднения уравнений Навье Стокса,
• Дата: 04.09.2018
• Размер: 1.55 Mb.
• Имя файла: Закон Дарси.docx
• Тип: Закон; #49764
• страница: 1 из 8

Возведение гидроэнергетических, гидромелиоративных, промышленных, гражданских и транспортных сооружений сопровождается различного рода устройствами (перемычками, водопонизительными скважинами, иглофильтрами, дренами и другими). Соответствующие расчеты фильтрации позволяют выбрать рациональные в экономическом отношении схемы водопонижения, обеспечивающие бесперебойную работу в котлованах и выработках в период строительства. В ходе вебинара рассмотрены вопросы расчета фильтрации грунтовых вод, приведены примеры расчета притока воды в котлован, расчет дамб и плотин

Закон Дарси (Анри Дарси, 1856) -- закон фильтрации жидкостей и газов в пористой среде. Исторически закон был получен А.Дарси экспериментально[1], но может быть получен с помощью осреднения уравнений Навье - Стокса, описывающих течение в масштабе пор[2] (в настоящее время имеются доказательства для пористых сред с периодической[3][4] и случайной[5] микроструктурой). Выражает зависимость скорости фильтрации флюида от градиента напора:

где: -- скорость фильтрации, -- коэффициент фильтрации, -- градиент напора[6].

Проверке и исследованию пределов применимости закона Дарси посвящено значительное число работ отечественных и зарубежных специалистов. В процессе этих исследований показано, что можно выделить верхнюю и нижнюю границы применимости закона Дарси и соответствующие им две основные группы причин.

1) Верхняя граница определяется группой причин, связанных с проявлением инерционных сил при достаточно высоких скоростях фильтрации.

2) Нижняя граница определяется проявлением неньютоновских реологических свойств жидкости, ее взаимодействием с твердым скелетом пористой среды при достаточно малых скоростях фильтрации.

Рассмотрим каждый из этих предельных случаев, которые приводят к нелинейным законам фильтрации.

Наиболее полно изучены отклонения от закона Дарси, вызванные проявлением инерционных сил при увеличении скорости фильтрации. Верхнюю границу применимости закона Дарси связывают обычно с некоторым критическим (предельным) значением числа Рейнольдса1

где d- некоторый характерный линейный размер пористой среды; v-кинематический коэффициент вязкости флюида

Многочисленные экспериментальные исследования и, в частности, опыты Дж. Фэнчера, Дж. Льюиса и К. Бернса, Линдквиста, Г. Ф. Требина, Н.М. Жаворонкова, М.Э. Аэрова и других были направлены на построение универсальной зависимости (по аналогии с трубной гидравликой) коэффициента гидравлического сопротивления l от числа Рейнольдса. Однако вследствие различной структуры и состава пористых сред получить такую универсальную зависимость не удается.

При обработке результатов экспериментов значительное внимание обращалось на такой выбор характерного размера поровой структуры, чтобы отклонения от закона Дарси возникали при одинаковых значениях числа Рейнольдса, и закон фильтрации в нелинейной области допускал универсальное представление.

Первая количественная оценка верхней границы применимости закона Дарси была дана более 60 лет назад Н. Н. Павловским, который, опираясь на результаты Ч. Слихтера, полученные для модели идеального грунта, и полагая характерный размер d равным эффективному диаметру dэф вывел следующую формулу для числа Рейнольдса

(1.11)

Использовав эту формулу и данные экспериментов, Н.Н. Павловский установил, что критическое значение числа Рейнольдса находится в пределах

Достаточно узкий диапазон изменения значений Reкр объясняется тем, что в опытах использовались не слишком разнообразные образцы пористых сред.

Для удобства обработки результатов многочисленных экспериментов различных авторов В. Н. Щелкачев предложил использовать безразмерный параметр, названный им параметром Дарси и определяемый равенством

Отсюда видно, что параметр Дарси представляет собой отношение силы вязкого трения к силе давления. Сравнивая равенство (1.12) и закон Дарси (1.7) (для случая горизонтального пласта, когда р* = р), можно утверждать, что если справедлив закон Дарси, то

Таким образом, равенство (1.13) должно выполняться при

Введение параметра упрощает исследование границы применимости линейного закона фильтрации. Действительно, если на оси абсцисс откладывать а по оси ординат то поскольку при графиком зависимости от будет прямая линия, совпадающая с осью абсцисс до тех пор, пока .

Как только на этом графике линия начнет отделяться от оси абсцисс, сразу же обнаружится нарушение закона Дарси (это соответствует значениям ). Значение при котором станет заметно отклонение упомянутой линии от оси абсцисс, и будет критическим значением. Для иллюстрации сказанного на рис. 1.5 на логарифмической сетке приведены зависимости от , представляющие результат обработки опытов по формулам В. Н. Щелкачева (табл. 1.1). Данные на этом графике соответствуют области нелинейной фильтрации для различных образцов пористых сред.

Основываясь на этих соображениях, В. Н. Щелкачев провел критический анализ и сравнение формул, полученных разными исследователями, для определения в подземной гидромеханике и оценки возможных критических значений числа Рейнольдса соответствующих верхней границе применимости закона Дарси. Результаты такого сопоставления приведены в табл. 1.1. В первых двух строках таблицы даны соответственно формулы для и коэффициента гидравлического сопротивления l, полученные разными авторами. В четвертой и пятой строках приведены соответственно критические значения полученные самими авторами, и их уточненные значения.

Наличие третьей строки табл. 1.1, в которой дано произведение объясняется следующим. В области линейного закона фильтрации справедливо равенство (1.13). Поэтому если произведение зависит только от параметра (см. графы 5-8 табл. 1.1), то оно имеет постоянное значение (не зависящее от свойств пористой среды) в случае, если И только в этом случае можно получить «универсальный» прямолинейный график в координатах соответствующий фильтрации различных флюидов через различные по свойствам пористые среды. Результаты обработки опытов подтверждают этот вывод.

Темп процесса консолидации вначале относительно велик, но с течением времени снижается. Несмотря на то, что значение конечной величины осадки проектируемого сооружения имеет большое значение, наибольший интерес представляет определение скорости осадки в первые годы жизни сооружения.

Степень соответствия сделанных Терцаги допущений практическим условиям Предположение, что грунт находится в водонасыщенном состоянии, достаточно справедливо в том случае, если сжимаемые глинистые грунты с ненарушенной структурой расположены глубже 1,2-1,5 м от поверхности земли.

Допущение, что вода и грунтовые частицы несжимаемы, как бы предполагает, что осадки, вызываемые упругим сжатием грунта, ничтожно малы по сравнению с осадками в результате консолидации. В большинстве случаев это вполне подтверждается на практике.

Закон Дарси достаточно близко соответствует экспериментальным данным. Однако предположение, что коэффициент фильтрации остается постоянным в течение процесса консолидации, остается спорным. Предположение, что грунт не деформируется в стороны, а вода выжимается из него только в вертикальном направлении, вероятно, является источником наибольших ошибок.

Эти ошибки тем меньше, чем на большую площадь грунта передается давление. Хотя можно показать, что сделанные предположения не очень близки к истине, все же во многих случаях расчетные осадки достаточно хорошо совпадают с фактически измеренными.

На основе перечисленных выше допущений и граничных условий, Терцаги вывел следующее уравнение зависимости осадки от времени, прошедшего после приложения к поверхности грунта равномерного давления.

Выражение для осадки водонасыщенного слоя — уравнение — содержит, таким образом, величину конечной осадки, умноженную на стоящее в скобках выражение, являющееся некоторой функцией фактора времени.

Углеводородные системы могут быть гомо– и гетерогенными. В гомогенной системе все ее части имеют одинаковые физические и химические свойства. Составляющие гомогенной системы (называемые компонентами) «размазаны» по всему пространству и взаимодействуют на молекулярном уровне. Для гетерогенной системы физические и химические свойства в разных точках различны. Гетерогенные системы состоят из фаз. Фаза — это часть системы, которая является гомогенной и отделена от других фаз отчетливыми границами. Смесь воды, нефти и газа в пласте — типичный пример гетерогенной среды.

Главными характеристиками движения многофазной системы являются насыщенность и скорость фильтрации каждой фазы.

Насыщенностьюσ_i — порового пространства i — й фазой называется отношение объема данной фазы V_i к объему пор V_пор, занятая этой фазой в элементарном …
объеме:

.

(3.1)

Очевидно, что

.

(3.2)

Таким образом, в n — фазной системе имеется (n — 1) независимая насыщенность. В частности, при исследовании фильтрации смеси двух фаз используется лишь одна из насыщенностей, которая обозначается в дальнейшем а (обычно это насыщенность вытесняющей фазы). В пористой среде наиболее часто происходит фильтрация воды, нефти и газа, поэтому будем обозначать насыщенности этих фаз σ_в, σ_ни σ_г.

Закон Дарси для течения в пористой среде однородной жидкости можно распространить на случай совместного течения двух и более несмешивающихся жидкостей, обобщив понятие проницаемости.

Прежде всего введем понятие скорости фильтрации данной фазы. Скоростью фильтрации данной фазы называется отношение расхода данной фазы к площади поперечного сечения

.

(3.3)

Площадка ω пересекает твердую и обе подвижные фазы.

Экспериментально установлено, что расход каждой фазы растет с увеличением перепада давления и насыщенности данной фазой, а закон фильтрации каждой из фаз по аналогии с законом Дарси можно записать в виде

.

(3.4)

где u_i — скорости фильтрации i – той фазы; μ_i – динамический коэффициент вязкости; k_i^* – фазовые проницаемости. Величины k_i^* (i = 1, 2) являются для i  той жидкости проницаемостями в обычном смысле в условиях совместной фильтрации. Эти величины зависят от природы пористой среды (и, прежде всего, от ее абсолютной проницаемости k, определяемой по данным о фильтрации однородной жидкости), а также от насыщенности пористой среды каждой фазой. При описании многофазных течений обычно вместо фазовых проницаемостей k_i^* вводят так называемые «относительные фазовые проницаемости» kiопределяемые из отношений

.

(3.5)

В большинстве опытов показано, что для данной структуры пористой среды относительные проницаемости k_i являются в основном функциями насыщенности, а если и наблюдается влияние иных параметров (например, отношения коэффициентов вязкости фаз), то им обычно пренебрегают. Для примера запишем обобщенный закон Дарси при фильтрации трехфазной системы вода – нефть – газ вдоль направления s.

.

(3.6)

Для двухфазной системы вода – нефть приближенные эмпирические формулы для относительных фазовых проницаемостей имеют вид:

(3.7)

Здесь обозначено σ_во, σ_но – остататочные водо и нефте насыщенности.

Для двухфазной системы вода – газ приближенные эмпирические формулы для относительных фазовых проницаемостей имеют вид:

(3.8)

Здесь обозначено σ_во, σ_но, σ_го – остататочные водо, нефте и газо насыщенности.

Типичный вид экспериментальных кривых фазовых проницаемостей k_в(s_в), k_н(s_н), k_г(s_г) приведен на рис. 3.1. Отметим некоторые характерные особенности этих кривых. Для каждой фазы существует предельные насыщенность s_во, s_но, s_го, которые называются остаточными насыщенностями. Движение каждой фазы может происходить только в том случае, если насыщенность этой фазы больше остаточной насыщенности для этой фазы. Таким образом, совместное течение двух фаз (например вода – нефть) имеет место лишь в следующем интервале изменения водонасыщенности для воды σ_во, < σ_в < 1 — σ_но.

Нефтенасыщенность связана с водонасыщенностью σ_н, = 1 — σ_в, поэтому совместное течение происходит при нефтенасыщенностях σ_но, < σ_н < 1 — σ_во.

При движении двухфазной системы (вода – нефть или вода – газ) удобно относительные фазовые проницаемости представлять на одном графике в зависимости фазовых проницаемостей от водонасыщенности рис. 3.3.

Сумма относительных проницаемостей для каждого фиксированного значения а меньше 1.

Предельное статическое и динамическое напряжения сдвига. Тиксотропия.(ПДНС и ПСНС)



ПДНС – характеризует прочностное сопротивление бурового раствора.

ПДНС – усилие, которое необходимо применить к раствору, чтобы вызвать ламинарное течение.

На практике фактической мерой ПДНС яв-ся предельное статическое напряжение сдвига (ПСНС).

ПСНС – характеризует прочность тиксотропной структуры, возникающей в покоящемся буровом растворе и интенсивность упрочнения ее во времени. Если через увеличивающиеся периоды покоя раствора СНС возрастают до максимального значения, то это явление называется тиксотропией (превращение золя в гель). При этом происходит медленная переориентация глинястых пластинок в направление с минимально свободной поверхностной энергией.

При высоких значениях СНС > 100 дека ПА из-за резкого снижения гидростатического давления до 30кгс/см³ появляются проблемы при пуске насосов, дополнительные энергетические затраты, отсутствие оседания шлака, возможный гидроразрыв пласта и выброс.



1:10 -> 1 к 10 мин. Измерение t при выдержке в покое раствора. Обычно ᶿ10 на 50+- 10% > ᶿ1



 

 

Вопрос 5

Модели фильтрационного течения.

Сложный и нерегулярный характер структуры порового пространства не позволяет изучать движение флюидов в нем прямым решением уравнения движения вязкой жидкости для каждого порового канала или трещины. В процессе движения флюиды испытывают различные деформации(сжатие, кручение). При изменении нагрузок (трении соседних объемов), которое отнесенное к единице площади получило название напряжение. Само соотношение, связывающее деформацию и скорость изменения деформации с напряжением называют реологическим законом.

Наиболее часто применимо к жидкостям для описания действия касательных напряжений  на сдвиговую деформацию применяется соотношение ньютона:

 =ᶯ 

 -скорость в направлении х

 - направление перпендикулярно х

ᶯ - коэффициент динамической вязкости.

Довольно часто движение флюидов не подчиняется данному закону. Например, при трогании пластовой нефти требуется некоторое, отличное от нулевого напряжения, чтобы разорвать образованные пластовой водой коллоидные структуры, такие среды называются неньютоновскими, а их модель – моделью неньютоновского течения.



 

Вопрос 6
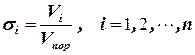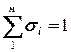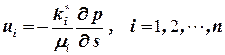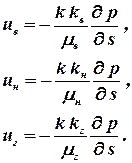