Курсовая работа 1 Учебная дисциплина Теория телетрафика Таран Валентина Александровна

• Название: Курсовая работа 1 Учебная дисциплина Теория телетрафика Таран Валентина Александровна
• Дата: 19.05.2019
• Размер: 1.9 Mb.
• Имя файла: TT_139030.doc
• Тип: Курсовая; #77724

САНКТ-ПЕТЕРБУРГСКИЙ

ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ

им. проф. М. А. БОНЧ-БРУЕВИЧА

1. 
   Факультет вечернего и заочного обучения
   

КУРСОВАЯ РАБОТА №1
Учебная дисциплина

Теория телетрафика


Выполнила:

Таран Валентина Александровна

№ студ. билета 139030

Группа: АБ-39с, 3 курс

САНКТ-ПЕТЕРБУРГ

2016

Задание 2 Исследование процесса обслуживания реального потока сообщений полнодоступным пучком, включенным в однозвенную коммутационную схему

Условие:

На телефонной станции организован станционный эксперимент, направленный на выявление соответствия реального процесса обслуживания потоков сообщений математическим моделям, описываемым первой формулой Эрланга и формулой Энгсета. Условия эксперимента ограничены однозвеньевой ступенью свободного искания, в выходы которой включен полнодоступный пучок из ν линий. Поток создается N источникам; среднее число вызовов в ЧНН от всех источников составляет ; средняя длительность обслуживания одного сообщения принята равной . Измерения числа i одновременно занятых линий в пучке проводятся в течение 3 дней по 12 измерений каждый ЧНН.
Необходимо:

Оценить следующие характеристики процесса обслуживания.

1. 
   По результатам измерений рассчитать следующие эмпирические значения:
   

- интенсивности нагрузки ,обслуженной ступенью искания;

- интенсивности нагрузки , поступающей на ступень искания;

- интенсивности нагрузки , потерянной ступенью искания;

2. 
   В предположении, что поступающий на ступень искания реальный поток сообщений соответствует модели простейшего потока, для которого среднее число вызовов в ЧНН от всех источников (Т – промежуток времени, соответствующий ЧНН), рассчитать:
   

- интенсивность нагрузки , поступающей на ступень искания;

- вероятность того, что все линий пучка заняты ;

- вероятность потерь по вызовам Р_в, времени Р_t, нагрузке Р_н;

- распределение вероятностей Р_i, i=0,1,..,;

- интенсивность нагрузки , обслуженной ступенью искания;

- интенсивность нагрузки , потерянной ступенью искания;

- отклонение теоретического значения вероятности потерь Р_н от эмпирического значения , в %;

- отклонение теоретического значения интенсивности обслуженной нагрузки от эмпирического значения , в %.

3. 
   В предположении, что поступающий на ступень искания реальный поток сообщений соответствует модели примитивного потока, который создает нагрузку интенсивности (а – интенсивность нагрузки, поступающей от одного источника), рассчитать:
   

- вероятность потерь по вызовам Р_в;

- вероятность потерь по времени Р_t;

- вероятность потерь по нагрузке Р_н;

- распределение вероятностей Рi, i=0,1,…,;

- среднее значение параметра потока от N источников;

- интенсивность нагрузки , обслуженной ступенью искания;

- интенсивность нагрузки , потерянной ступенью искания;

- отклонение в процентах теоретического значения вероятности потерь Р_н от эмпирического значения ;

- отклонение теоретического значения интенсивности обслуженной нагрузки

4. 
   Построить кривые распределения Эрланга и Энгсета и получить численное доказательство того, что сумма вероятностей состояний полнодоступного пучка при обслуживании примитивного и простейшего потока вызовов составит
   

5. 
   Установить взаимосвязь между рассматриваемыми моделями, выявив условия перехода формулы Энгсета в первую формулу Эрланга.
   
6. 
   По результатам проведенных исследований сформулировать выводы относительно соответствия процесса обслуживания реального потока сообщений математическим моделям, описываемым первой формулой Эрланга и формулой Энгсета.
   

Таблица 5 – Результаты измерений числа одновременно занятых линий

	1	2	3	4	5	6	7	8	9	10	11	12
1 день	2	6	5	6	4	10	7	3	5	5	4	3
2 день	4	7	4	3	6	8	5	3	5	2	7	6
3 день	5	10	6	2	5	3	4	3	4	5	3	2

Таблица 6 – Исходные данные

с	t, c	ν	N
240	75	10	40

Решение:

1. 
   Интенсивность обслуженной нагрузки определяется как
   

, где

- число одновременно занятых линий при каждом измерении (k = 1,2,..,12) в j-й день измерений (j = 1,2,3).

Для 1 дня: = 2+6+5+6+4+10+7+3+5+5+4+3 = 60

Для 2 дня: = 4+7+4+3+6+8+5+3+5+2+7+6 = 60

Для 3 дня: = 5+10+6+2+5+3+4+3+4+5+3+2 = 52


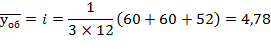Интенсивность поступающей нагрузки: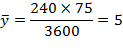




Интенсивность потерянной нагрузки:





Вероятность потерь по нагрузке: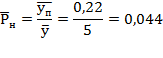

2. 
   Предположим, что поступающий поток вызовов является простейшим потоком. Для его полного описания достаточно знать интенсивность потока μ, зная которую можно оценить все остальные характеристики потока (параметр λ, функцию распределения промежутков между вызовами А(х), вероятность поступления определенного числа вызовов k за некоторый промежуток времени t – P_k(t)).
   

Если принять за единицу времени ЧНН, то правомерно приравнять эмпирическое значение среднего числа вызовов в ЧНН его теоретическому значению:

.

Переходя к расчету характеристик модели обслуживания М/М/ν/К (процесс обслуживания простейшего потока вызовов полнодоступным пучком линий с потерями при показательном распределении длительности обслуживания), К=ν, также правомерно приравнять эмпирическое значение интенсивности поступающей нагрузки его теоретическому значению у:



Модель М/М/ν/К, К=ν описывается первым распределением Эрланга: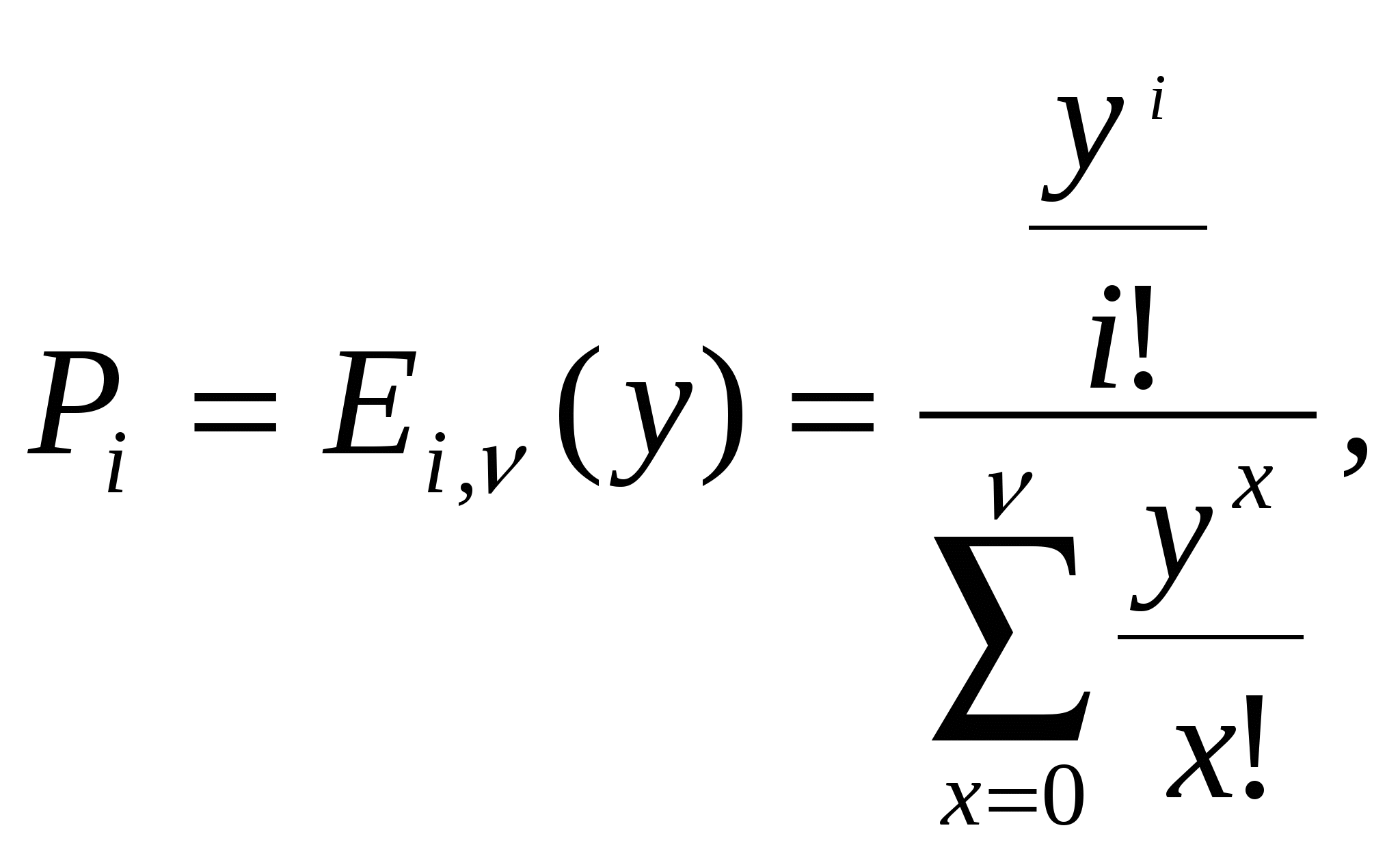



Р₁₀ = 0,01838

Р₉ = 0,03677

Р₈ = 0,06618

Р₇ = 0,1059

Р₆ = 0,14825

Р₅ = 0,17790

Р₄ = 0,177904

Р₃ = 0,142323

Р₂ = 0,085394

Р₁ = 0,034158

Р₀ = 0,02522

где -вероятность того, что в полнодоступном пучке из ν линий, на который поступает нагрузка интенсивности у, занято точно i линий .

Вероятность занятости в пучке всех ν линий Р_ν равна вероятности потерь по вызовам Р_в, времени Р_t и нагрузке Р_н: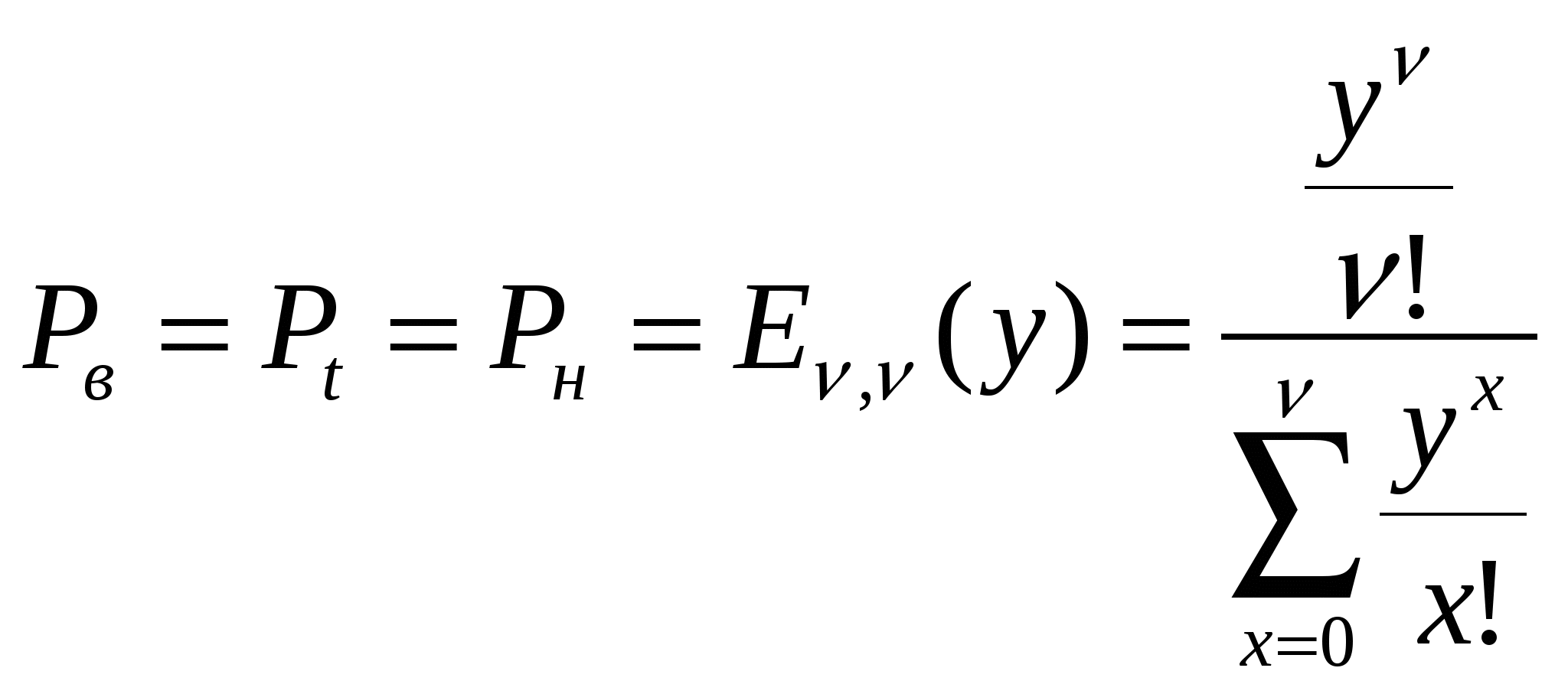



Согласно таблицам из Приложения 2 вероятность занятости в пучке всех ν линий Р_ν равна 0.018385, т.е.

Интенсивность обслуженной нагрузки равна:



Интенсивность потерянной нагрузки:



Определим отклонения теоретических значений Р_н и у_об от эмпирических, 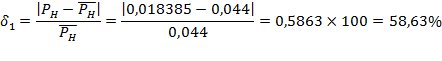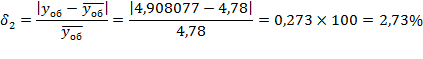и , в %:

3. 
   Предположим, что поступающий поток вызовов является примитивным, который характеризуется переменным параметром λ_i, пропорциональным числу свободных источников (абонентов):
   

где N – общее число источников, i – число занятых источников, α – параметр потока одного свободного источника.

В сущности, примитивный поток – это суммарный поток, т.е. от каждого свободного источника поступают простейшие взаимно независимые потоки.

Модель обслуживания примитивного потока полнодоступным пучком (модель М/М/ν/K/N, К=ν) описывается формулой Энгсета.

Распределение Энгсета P_i и характеристики качества прохождения нагрузки имеют следующий вид: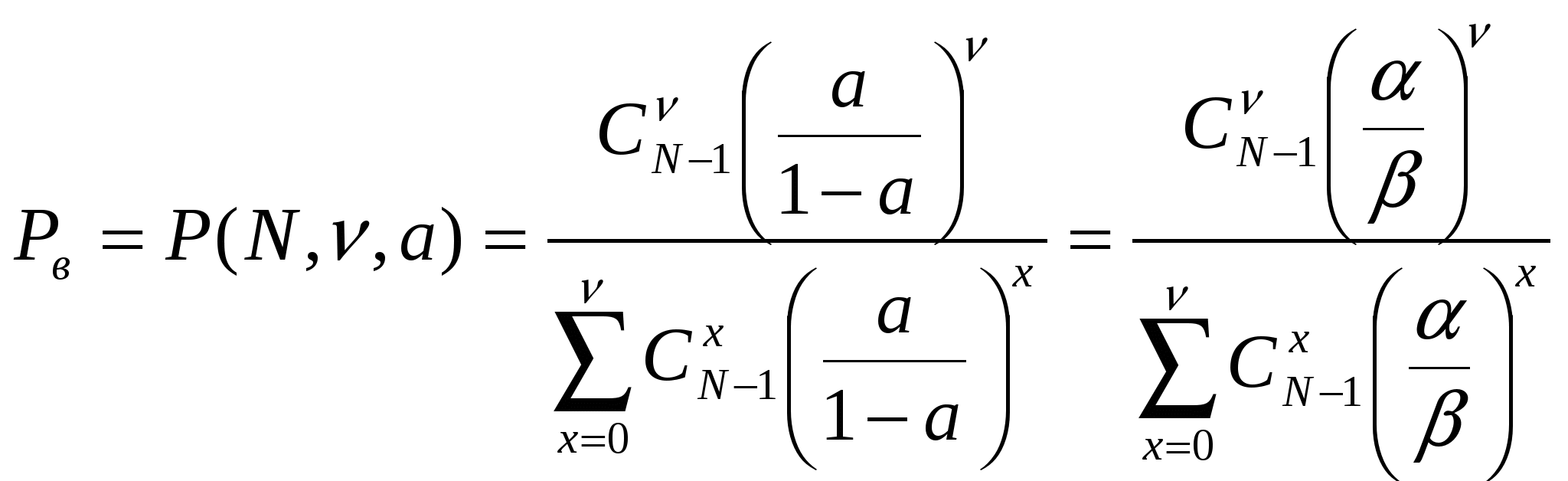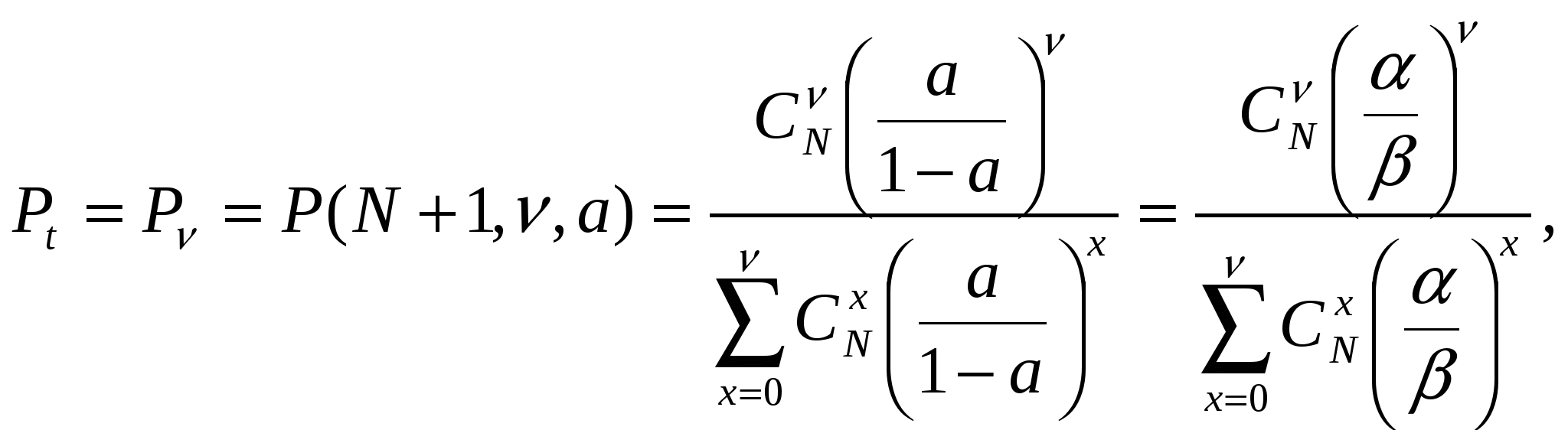







,

при этом Р_н < P_в < P_t = P_ν, где α/β= α×1/β – среднее число вызовов, посылаемое одним свободным источником в течение интервала времени, равного средней длительности обслуживания;

- нагрузка, создаваемая одним источником, т.е. отношение средней длительности обслуживания к сумме средней длительности обслуживания и расстояния от момента окончания обслуживания до момента посылки нового вызова.

Нагрузка, создаваемая одним источником равна: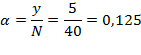


Тогда согласно Приложению 3:

Р_в = 0,012405

P_t = P_ν = 0,014494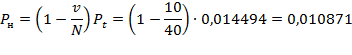



Распределение вероятностей P_i рассчитывается через рекуррентное соотношение, начиная с i=ν: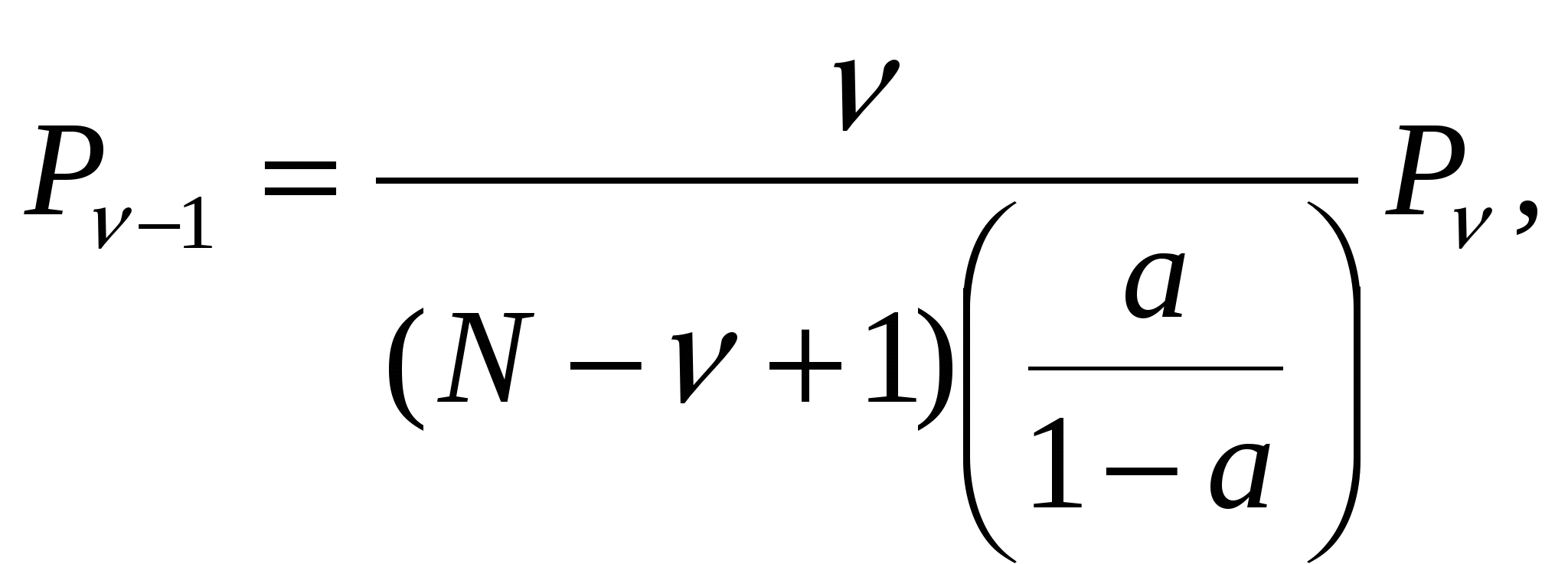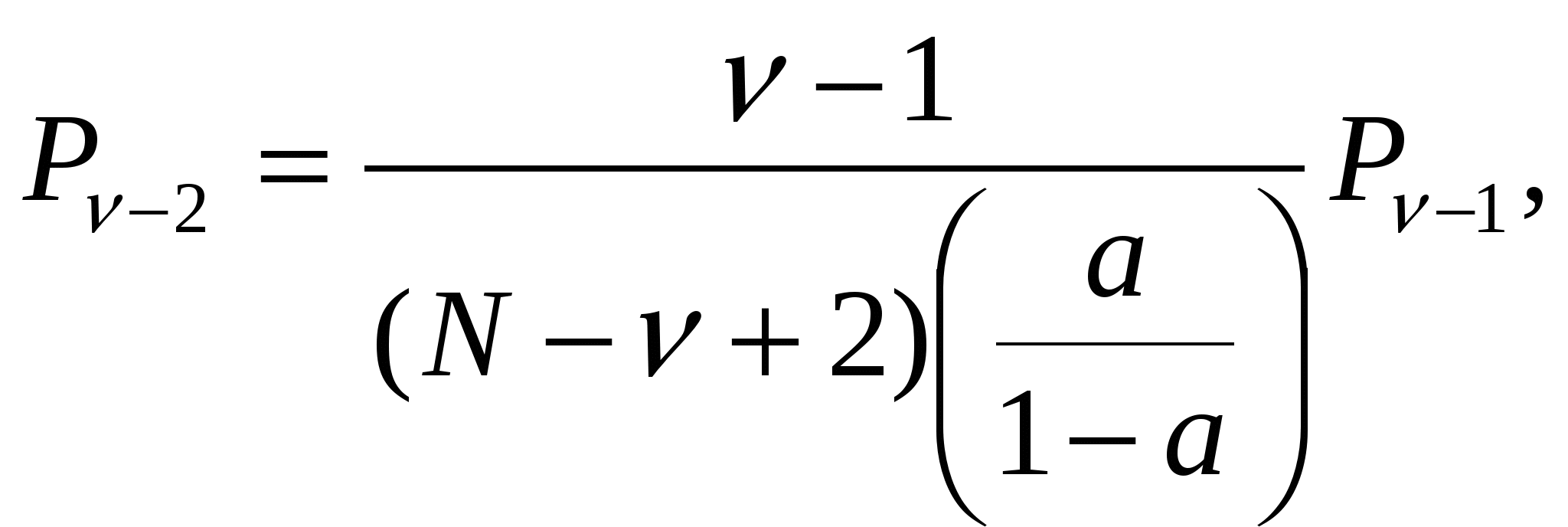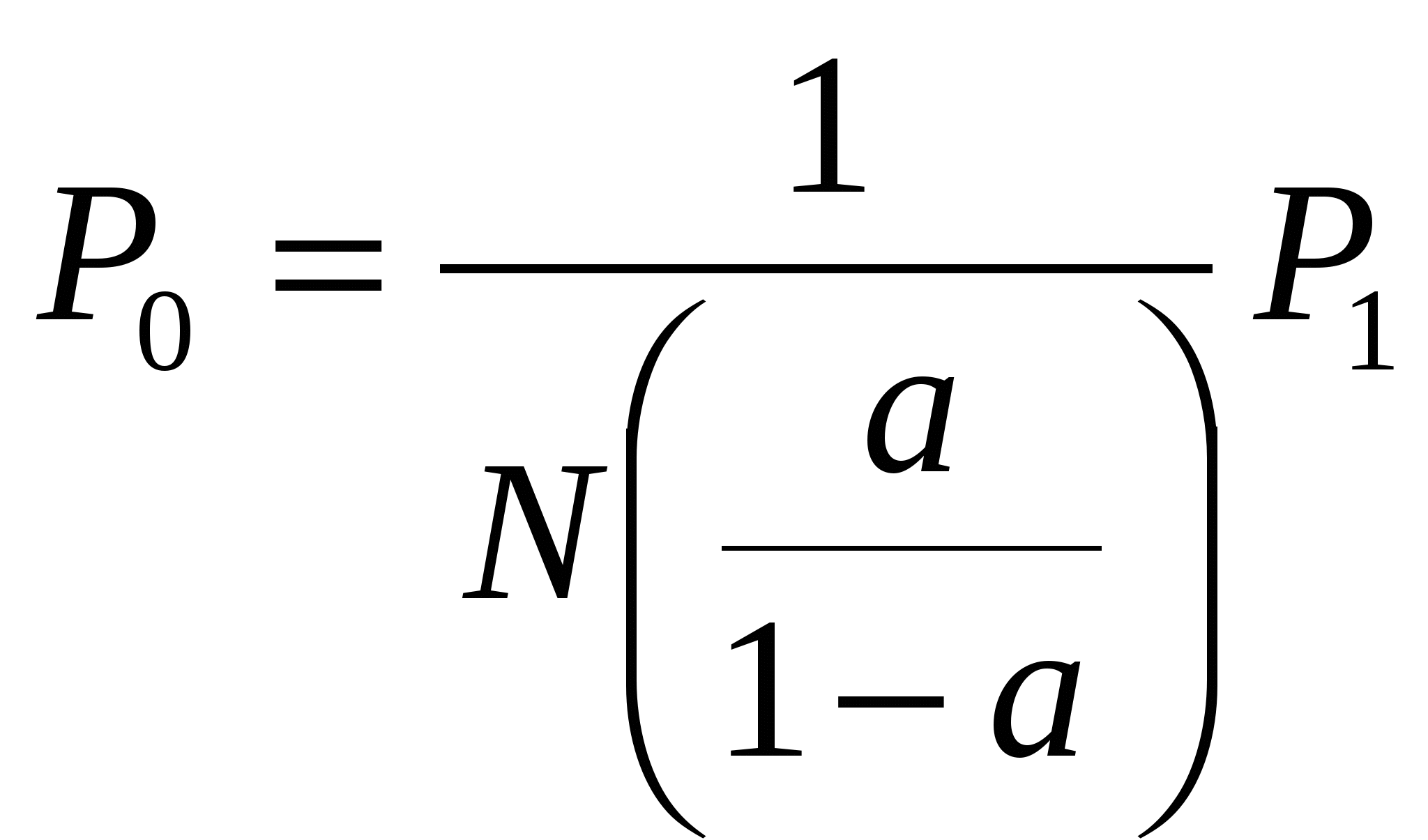





. . . . . . .



Р₁₀ = 0,012405

Р₉ = 0,03273

Р₈ = 0,06444

Р₇ = 0,10935

Р₆ = 0,15759

Р₅ = 0,18910

Р₄ = 0,18385

Р₃ = 0,13913

Р₂ = 0,07689

Р₁ = 0,0276

Р₀ = 0,01932

При расчете характеристик модели М/М/ν/К/N, К=ν будем исходить из численного равенства между эмпирическим значением интенсивности поступающей нагрузки и ее математическим ожиданием ().

Интенсивность поступающей нагрузки на ν линий от N источников (по определению среднего значения)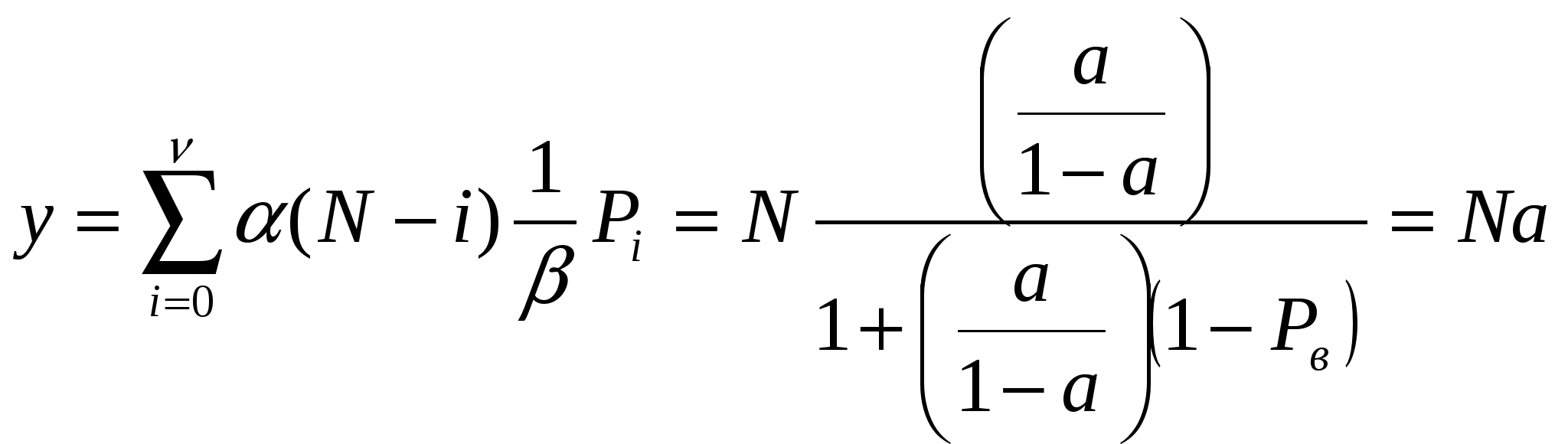





Интенсивность обслуженной нагрузки (среднее число занятых линий i):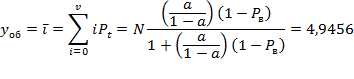


Интенсивность потерянной нагрузки: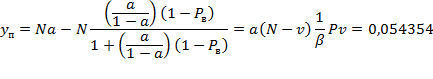



Определим отклонения теоретических значений Р_н и у_об от эмпирических, 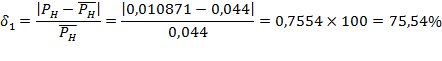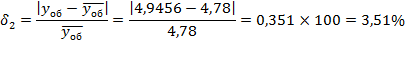и , в %:

4. 
   Сумма вероятностей состояний полнодоступного пучка при обслуживании примитивного и простейшего потоков составляет 1:
   

Это легко доказать.

Для простейшего потока:

0.01838+0.03677+0.06618+0.1059+0.14825+0.17790+0.177904+0.142323+

+0.085394+0.034158+0.02522 = 1

Для примитивного потока:

0.012405+0.03273+0.06444+0.10935+0.15759+0.18910+0.18385+0.13913+0.07689+

+0.0276+0.01932 = 1

5. 
   Характер зависимости величины поступающей нагрузки na от емкости пучка линий v, который обслуживает вызовы примитивного потока, поступающие от фиксированного числа источников n, такой же, как при обслуживании вызовов простейшего потока. Однако на пропускную способность пучка влияет число источников вызовов n: в области малых потерь с уменьшением n увеличивается пропускная способность пучка. При увеличении потерь Р_в:
   

- существенно уменьшается влияние n на пропускную способность пучка;

- сокращается различие между пропускной способностью пучков, обслуживающих вызовы примитивного и простейшего потоков.

6. 
   По результатам проведенных исследований можно сопоставить реальный поток обслуживания вызовов и две математические модели: простейший поток и примитивный поток.
   

У простейшего потока интенсивность обслуженной нагрузки отличается от реальной на 2.73%, а у примитивного потока – на 3.51%.

Вероятность потерь по нагрузке отличается от реального потока на 58.63 %, у примитивного – на 75.54 %.

Таким образом, приходим к выводу, что наш поток по своим характеристика ближе к простейшему потоку, эта модель описывает его более точно, чем примитивный поток.

Задание 3 Оценка пропускной способности управляющих устройств систем коммутации

Условие

Ступень группового искания (ГИ) координатной АТС с индивидуальными управляющими устройствами (маркерами) для каждого блока комплектуется из s коммутационных блоков. Средняя длительность занятия входа ступени ГИ равна t_вх. На ступень искания поступает поток вызовов, создающий нагрузку y_вх. Управляющие устройства работают по системе с ожиданием. Средняя длительность занятия одним вызовом управляющего устройства равна h, допустимое время – t_доп.

Необходимо

Оценить следующие характеристики процесса обслуживания.

1. Рассчитать качественные показатели работы управляющих устройств ступени ГИ при постоянной и показательно распределенной длительности обслуживания:

- вероятность задержки вызова P{γ>0};

-вероятность ожидания P{γ>t} свыше допустимого времени t для любого поступающего вызова при фиксированных значениях t_доп;

_- вероятность ожидания P₁{γ>t} свыше допустимого времени t для задержанного вызова при фиксированных значениях t_доп;

- среднее время ожидания для любого поступившего вызова;

- среднее время ожидания для задержанного вызова.

2. Рассчитать среднее число ожидающих вызовов (среднюю длину очереди) при показательном распределении длительности обслуживания.

3. По результатам расчетов построить и проанализировать следующие графические зависимости:

- P{γ>t} = f(t) и P₁{γ>t} = f(t) для однолинейного пучка, если удельная поступающая нагрузка на управляющие устройства при постоянной длительности обслуживания равна с;

- P{γ>t} = f(t) и P₁{γ>t} = f(t) для однолинейного пучка, если удельная поступающая нагрузка на управляющие устройства при показательном распределении длительности обслуживания равна с.

4. Произвести анализ полученных результатов и сделать вывод о характере изменений P{γ>t} и P₁{γ>t}) при увеличении t_доп и с, а также об изменении и с ростом с при прочих равных условиях для различных законов распределения длительности обслуживания.

Значения исходных данных приведены в таблице 1.

Таблица1 – Исходные данные

S	tвх, с	yвх, Эрл	h, с	tдоп1, c	tдоп2, c	tдоп3, c
10	76	560	0,66	0,99	1,98	3,3

Решение

В соответствии с классификацией Кендала процесс обслуживания простейшего потока вызовов полнодоступным пучком линий при показательном распределении длительности обслуживания и неограниченном числе мест для ожидания соответствует математической модели M/М/v, а тот же процесс при постоянной длительности обслуживания вызова – математической модели М/D/v, причем M/М/v описывается вторым распределением Эрланга, а М/D/v описывается кривыми Кроммелина.

Второе распределение Эрланга и характеристики качества прохождения нагрузки имеют следующий вид: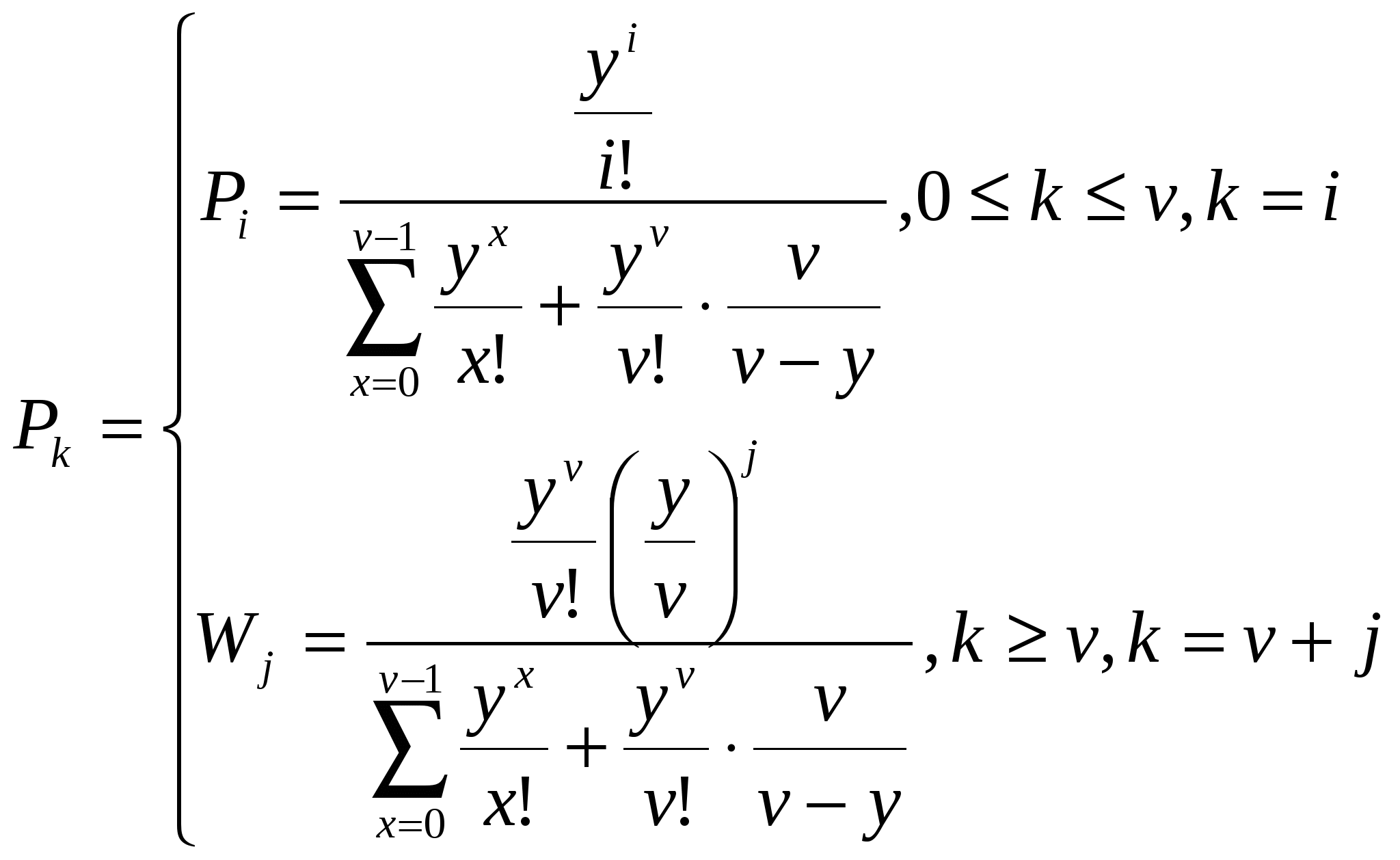



Формулы 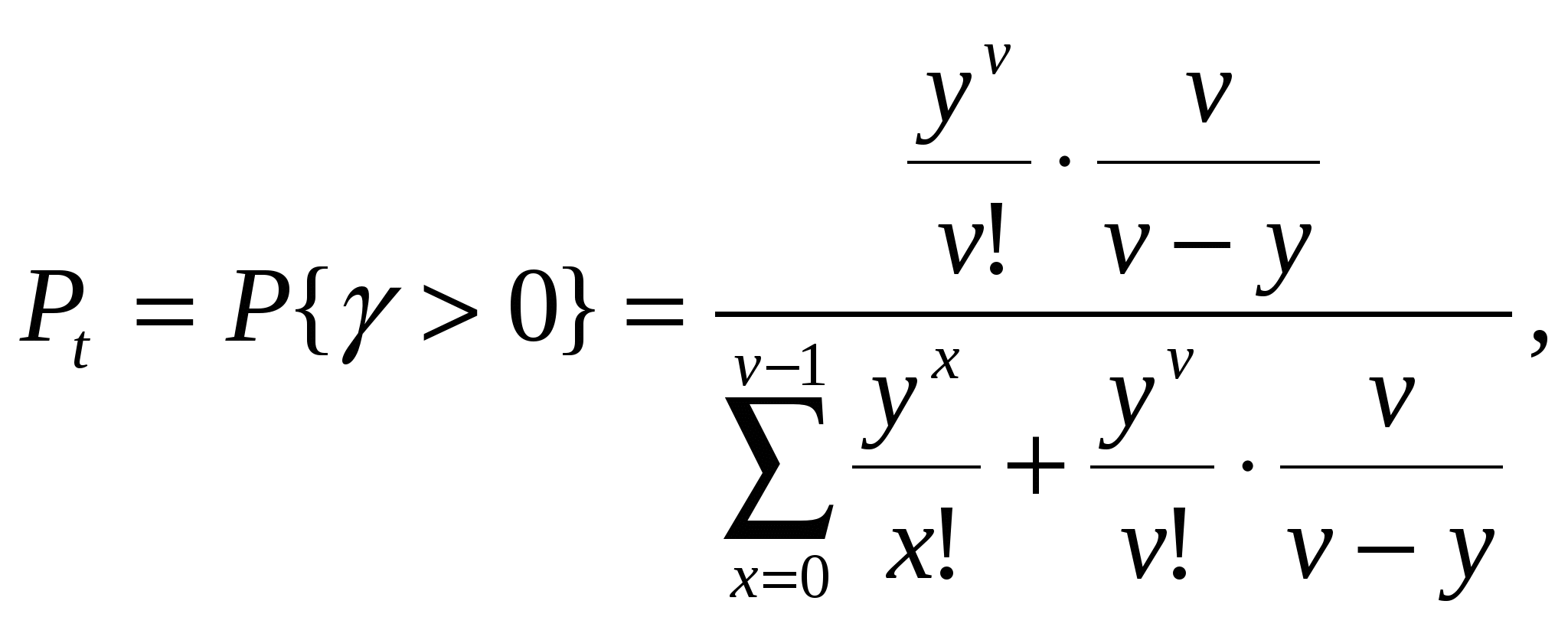и табулированы и представлены кривыми Кроммелина.





Определение качественных показателей обслуживания управляющими устройствами поступающей нагрузки должно производиться по расчетному значению нагрузки y_р.

Расчетное значение y_р обеспечивает требуемое качество прохождения нагрузки с заданной вероятностью ω, отклоняясь от математического ожидания нагрузки y по экспоненциальному закону



Определим расчетную нагрузку на одно управляющее устройство (маркер) ступени группового искания:

при v = 1, y = c () и P{γ>0} = f(c_p)

y_бл = yвх / с = 560/10 = 56 Эрл

y_pбл ==61,045 Эрл

Эрл

Для оценки качественных показателей работы управляющих устройств ступени искания при показательно распределенной и при постоянной длительностях обслуживания необходимо выразить допустимое время ожидания t_доп в условных единицах, численно равных длительности обслуживания маркером одного вызова, в с:



с

с

с

Далее необходимо вычислить следующие характеристики качества прохождения нагрузки: P{γ>0}, P{γ>t}, P₁{γ>t}= с использованием таблиц второй формулы Эрланга и кривых Кроммелина

Для математической модели М/М/v:

Вероятность задержки вызова P{γ>0} = с_р=0,53

Вероятность ожидания P{γ>t} свыше допустимого времени t для любого поступающего вызова при фиксированных значениях t_доп равна

Для

Для

Для

Вероятность ожидания P₁{γ>t} свыше допустимого времени t для задержанного вызова при фиксированных значениях t_доп равна P₁{γ>t}=

Для

Для

Для

Среднее время ожидания для любого поступившего вызова:

с

Среднее время ожидания для задержанного вызова:

с

Среднее число ожидающих вызовов равно

Эрл

На основании полученных результатов построим график 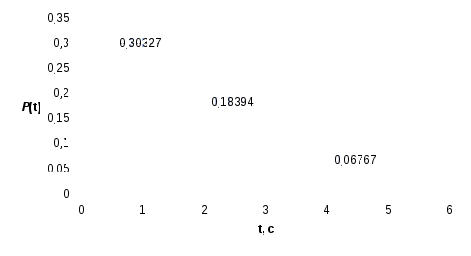и график


Рисунок 1 - График функции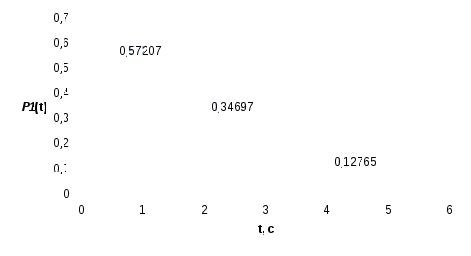


Рисунок 2 - График функции
Для математической модели М/D/v:

Вероятность задержки вызова P{γ>0} = с_р=0,53

Для нахождения вероятности ожидания P{γ>t} свыше допустимого времени t для любого поступающего вызова при фиксированных значениях t_доп воспользуемся кривыми Кроммелина

Для

Для

Для

Вероятность ожидания P₁{γ>t} свыше допустимого времени t для задержанного вызова при фиксированных значениях t_доп равна P₁{γ>t}=

Для

Для

Для

Среднее время ожидания для любого поступившего вызова:

с

Среднее время ожидания для задержанного вызова:

с

На основании полученных результатов построим график 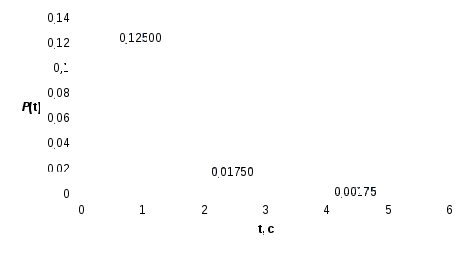и график



Рисунок 3 - График функции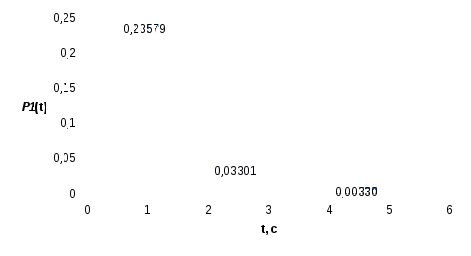



Рисунок 4 - График функции
Вывод

При увеличении в обоих случаях вероятности ожидания обслуживания свыше допустимого времени для любого поступающего и задержанного вызовов снижаются, но в случае с показательным распределением длительности обслуживания вероятность снижается плавно на всей временной оси, а при постоянной длительности занятия сначала резко уменьшается, а потом плавно и медленно уменьшается.

С ростом с_р среднее время ожидания для любого поступившего и для любого задержанного вызова начинает расти. Чем больше с_р, там дольше вызовам приходится ожидать обслуживания.

Задача 1. Исследование процесса поступления сообщений на системы коммутации
Условие: На телефонной станции организовано наблюдение за процессом поступления сообщений. Весь период наблюдения (25 ч), на протяжении которого поток является практически стационарным, разделен на n=100 интервалов длительностью t=15 мин. Для каждого интервала определяется число поступающих сообщений. Данные наблюдений группируются в статистический ряд по m членов, характеризующихся числом интервалов n_k (k = 1, 2, …, m) с одинаковым числом вызовов c_k в интервале

№ п/п	ck	nk
1	0	0
2	1	4
3	2	8
4	3	14
5	4	17
6	5	18
7	6	15
8	7	10
9	8	7
10	9	4
11	10	2
12	11	1
13	12	0
14	-	-
15	-	-
		100

Таблица 1. Исходные данные.
Требуется: Оценить следующие характеристики процесса поступления сообщений.

1. 
   Рассчитать эмпирические вероятности  распределения числа вызовов на интервале длительностью t = 15 мин.
   
2. 
   Рассчитать среднее статистическое значение числа вызовов  в интервале t=15 мин.
   
3. 
   Рассчитать вероятности распределения Пуассона P_k на интервале t=15 мин.
   
4. 
   Рассчитать число степеней свободы r и меру расхождения ² между теоретической вероятностью P_k и эмпирической 
   
5. 
   Определить соответствие эмпирического распределения числа сообщений в интервале t=15 мин распределению Пуассона
   

Решение

Эмпирические вероятности распределения числа вызовов рассчитываются по формуле

№ п/п	ck	nk
1	0	0	0
2	1	4	0,04
3	2	8	0,08
4	3	14	0,14
5	4	17	0,17
6	5	18	0,18
7	6	15	0,15
8	7	10	0,1
9	8	7	0,07
10	9	4	0,04
11	10	2	0,02
12	11	1	0,01
13	12	0	0
14	-	-	-
15	-	-	-
		100	1

Таблица 2. Эмпирические вероятности распределения числа вызовов
Среднее статистическое значение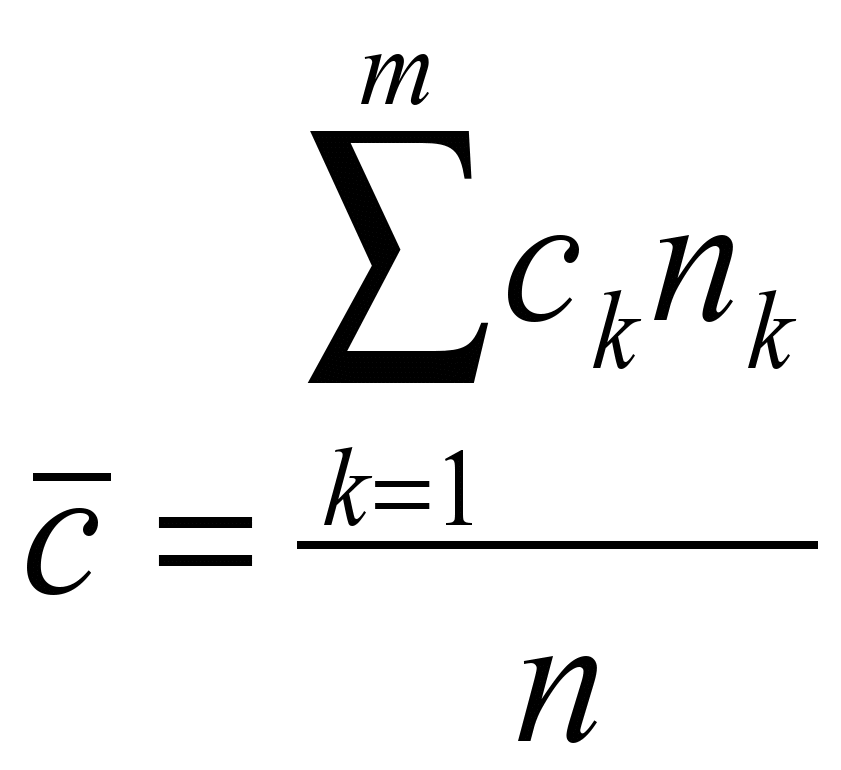

, где n – число интервалов наблюдения.
= 5,03
Значения вероятностей распределения Пуассона могут быть определены по справочным таблицам или рассчитаны по формуле

k	ck	Pk(t)
1	0	0
2	1	0,1839397206
3	2	0,1804470443
4	3	0,1680313557
5	4	0,1562934519
6	5	0,1462228081
7	6	0,137676978
8	7	0,1303774322
9	8	0,1240769173
10	9	0,118580076
11	10	0,1137363961
12	11	0,1094298885
13	12	0,1055703835
14	-	-
15	-	-

Таблица 3. Значения вероятностей распределения Пуассона

Число степеней свободы для данной задаче определяется как 

r = m – 2 = 13 – 2 = 11
Мера расхождения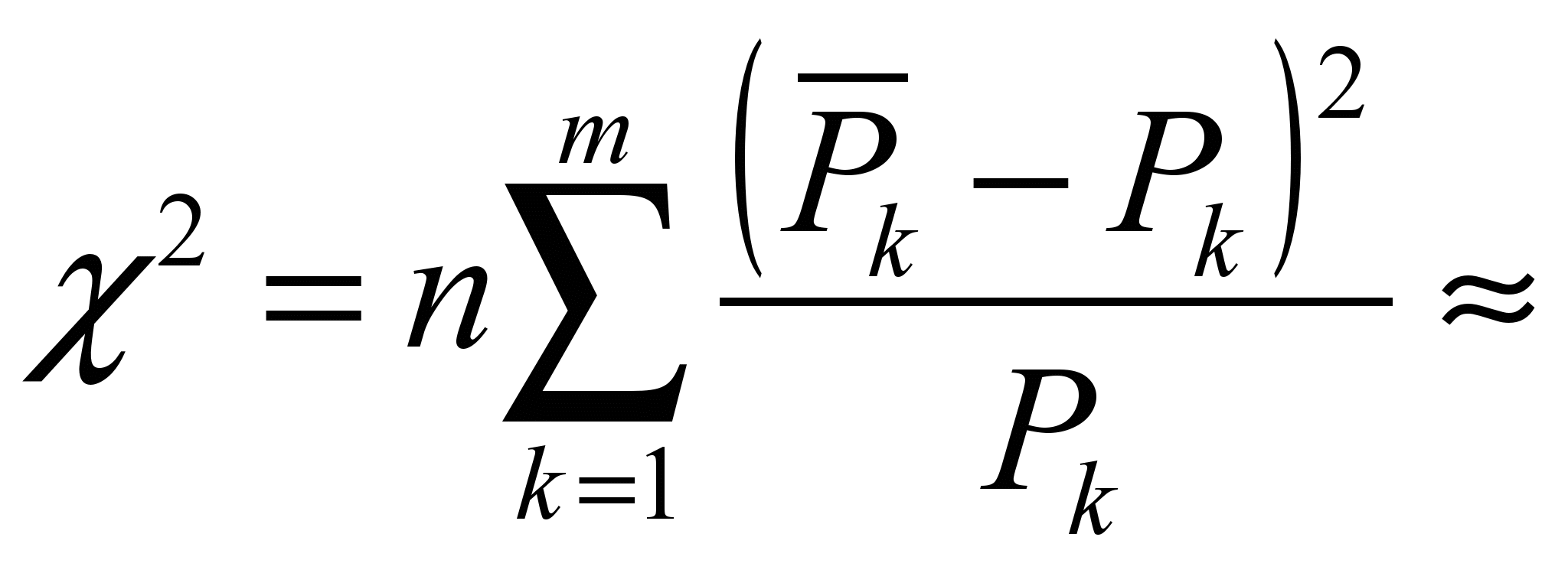 

54

Из таблицы P(r, ²) = 0,80