Анализ аварийных ситуаций на ПДК. курсовая Анализ аварийных ситуаций на ПДК. Курсовая работа Анализ развития аварийных ситуаций на пдк
 Скачать 303.89 Kb. Скачать 303.89 Kb.
|
|
Курсовая работа Анализ развития аварийных ситуаций на ПДК Студент: группы Матвеев А.А Преподаватель: _______________ Содержание Введение 3 1. Анализ развития аварийных ситуаций на ПДК 4 1.1. Общие данные 4 1.2. Исходные данные 6 1.3. Предварительная обработка и обобщение статистических данных 6 1.4. Проверка соответствия выбранного закона распределения случайных величин имеющимся статистическим данным 8 1.5. Определение статистических и теоретических значений вероятности безотказной работы P (x), отказа Q (x), частоты отказов a (x) и интенсивности отказов λ (x) для массива однородных случайных величин 10 Заключение 13 Список информационных источников 15 ВведениеВ настоящее время добыча нефти и газа на морских месторождениях получает все большее развитие в связи с невозможностью обеспечения возрастающего уровня потребления энергетических и сырьевых ресурсов за счет сухопутных месторождений. На территории российского континентального шельфа, включая арктический шельф, в ближайшее время прогнозируется открытие крупнейших и уникальных по своим запасам месторождений нефти и газа. Поэтому дальнейшее развитие отечественной нефтегазовой отрасли и ее энергетическое благополучие тесно связано с активным освоением континентального шельфа. Одним из самых перспективных направлений в освоении континентального шельфа становятся устанавливаемые на морском дне комплексные системы, не требующие ни стационарных, ни плавающих платформ. Подводный добычный комплекс (ПДК) - комплекс подводных устройств, систем и оборудования, предназначенный для обеспечения добычи пластовой продукции на морских нефтегазовых месторождениях с использованием скважин с подводным заканчиванием. Комплекс имеет важные преимущества по сравнению с оборудованием для добычных работ традиционными способами. Поскольку он находится целиком под водой, это позволяет избежать проблем, связанных с покрытием льдами водной поверхности, ледовый период к примеру, района Охотского моря составляет 7 месяцев в году. Применение подводных добычных комплексов (ПДК) приобрело в последние годы такой размах, что ведущие нефтегазовые компании столкнулись с необходимостью унифицировать условия их безопасной работы. Проблема обеспечения надежности - одна из важнейших при применении подводной технологии, поскольку инспекция подводного оборудования затруднена, а его обслуживание и (или) замена требуют больших затрат. Кроме того, отказ подводного оборудования непосредственно влияет на состояние окружающей среды. В данной курсовой работе выполнен анализ развития аварийных ситуаций на ПДК по заданным экспериментальным данным об отказах оборудования ПДК. 1. Анализ развития аварийных ситуаций на ПДК1.1. Общие данныеОбъекты анализа рисков- подводные объекты и их элементы, входящие в состав ПДК: - фундаменты, свайные основания и другие системы и элементы, обеспечивающие фиксацию ПДК в проектном положении; - защитные конструкции ПДК, предназначенные для предупреждения внешних воздействий; - барьерные конструкции ПДК; - устьевое оборудование добычных и нагнетательных скважин; - подводные насосные системы; - внутри промысловые подводные трубопроводы и выкидные линии; - системы сбора и подготовки продукции скважин, - подводные манифольды, сепараторы, компрессоры, арматура и другое технологическое оборудование; - системы отгрузки продукции; - системы энергообеспечения ПДК; - гибкие и динамические райзеры; - шлангокабели; - морские операции. Регулярный и полный учет аварийных ситуацийнеобходим для идентификации, анализа и контроля связанных с эксплуатацией ПДК опасностей. Сведения об авариях ПДК должны содержать описание условий в начале аварии, информацию по развитию аварии, физических и статистических моделей и мероприятий по борьбе с аварией. Наиболее опасными авариями являются повреждения и отказы, вызванные: - нарушением герметичности элементов и соединений ПДК в результате внешних воздействий; - образованием разрывов и трещин по сварным швам и основному металлу конструкций в связи с дефектами изготовления, нарушением технологии строительства; - сквозными коррозионными свищами; -не герметичностью соединений в эксплуатации. Методы оценки опасности и риска могут быть качественными и количественными. К качественным методам анализа риска относятся: - методы проверочного (опросного) листа (Check-List), Что будет, если...? (What-If); - анализ опасности и работоспособности (Hazard and Operability Study) - HAZOP; - анализ видов и последствий [критичности] отказов (Failure Mode and Effects [Criticality] Analysis) - FME[C]A. Количественные методы оценки опасности и риска используют: - логико-графические методы представления и анализа аварийных ситуаций (деревья отказов и событий, диаграммы состояния и другие); - включение и использование в расчетах количественных данных о характеристиках аварийных событий и процессов. При выборе методов оценки безопасности и риска следует учитывать: - поставленные цели и задачи; - соответствие данному этапу проектирования; - достаточность методического и информационного обеспечения; - достаточность статистических данных; - трудоемкость и продолжительность проведения оценки. Статистические данные об отказах объектов, работающих в одинаковых условиях до отказа всех объектов, являются однородным массивом случайных величин. Случайной величиной может быть - время безотказной работы; - объем выполненной работы; - время, затрачиваемое на устранение отказов и их последствий; - количество отказов за определенный промежуток времени и т. п. 1.2. Исходные данныеЗадание: Произвести статистическую обработку массива однородных экспериментальных данных об отказах объекта. Исходные данные (выработка, сут.)
1.3. Предварительная обработка и обобщение статистических данныхВариационный ряд при расположении статистических значений случайной величины в возрастающем порядке:
Минимальное и максимальное значения случайной величины определены из вариационного ряда: t´min = 27 сут., t´max = 690сут. Расчётная величина диапазона рассеивания полученных статистических данных: Т = t´max - t´min = 690 – 27 = 663 сут. Принятое количество интервалов к = 10. Тогда, величина интервала: Δt' = Т / к= 663 / 10 = 66,3 сут. После округления в большую сторону: Δt= 67 сут. Принятые граничные значения диапазона рассеивания: tmin = 27 сут., tmax = 27 + 67∙10 = 697 сут. Границы всех интервалов хi max и xi min, а также средние значения xi ср. интервалов записаны в таблице 1, графы 2,3. Количества отказов для всех полученных интервалов Δni и частости mi, рассчитаны по формуле: mi = Δni / N где N – количество объектов, для которых имеются экспериментальные данные; индекс i – номер рассматриваемого интервала; занесены в таблицу 1, графы 4,5. Таблица 1
По имеющимся статистическим данным построена гистограмма и ломаная- полигон частот отказов (рис.1). 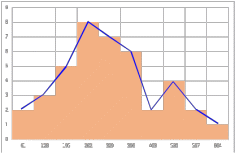 Рис.1 Гистограмма (красным) и полигон частот (синим) отказов 1.4. Проверка соответствия выбранного закона распределения случайных величин имеющимся статистическим даннымПо статистическим данным необходимо определить tср– среднее значение и S – среднее квадратичное отклонение для всего массива статистических данных по формулам: tср = 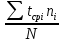 = = 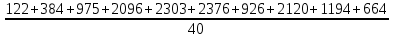 =329 сут. =329 сут.S = 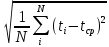 = = 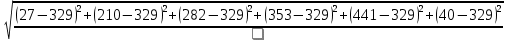 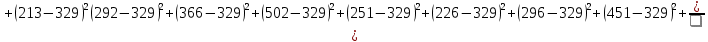 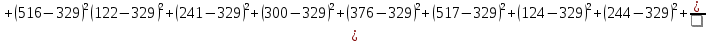 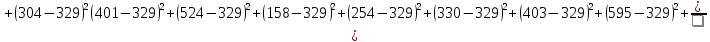 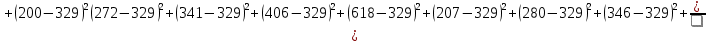 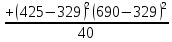 = = 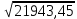 = 148,13 сут. = 148,13 сут.Для примера по закону распределения Вейбулла: f (x) = λ∙m∙xm- 1∙exp(- λ∙ xm); Вспомогательный параметр V = S / tср = 148,13 /329 = 0,45 По таблице зависимости между параметрами V и m распределения Вейбулла, определяем m = 2,25 Значение λ = 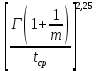 = = 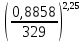 = 6,426 ∙10-7 = 6,426 ∙10-7По виду гистограммы можно предположить, что исследуемая величина имеет нормальный закон распределения с параметрами, а = tср = 329 сут; σ = S = 148,13сут. Теоретические значения функции плотности распределения отказов:
Полученные значения количества отказов n´i = f (tcp) ∙ Δt∙N записаны в таблице 2, графа 6. Производим проверку соответствия распределения статистических данных принятому закону распределения: 1. Графический способ - наиболее простой и наглядный способ проверки. На графике изменения частостей (гистограмме или полигоне распределения) построенном по статистическим данным, строится аналогичный график по полученным теоретическим данным (рис.2). 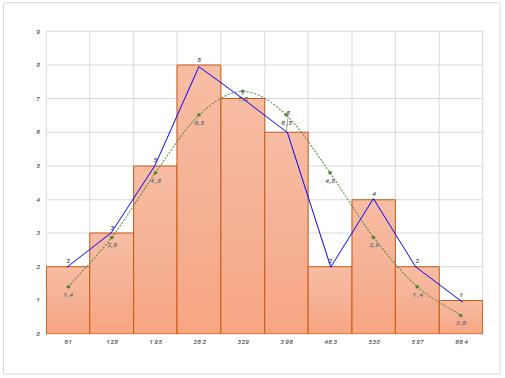 Рис.2 Гистограмма (красным) и полигон частот (синим) отказов, графикпо полученным теоретическим данным(зелёным) Теоретическая кривая в большей степени соответствует ломаной полигона частот. 2. По критерию Колмогорова. Необходимо определить накопленное количество отказов для каждого интервала по статистическим и теоретическим данным, а также d - модули их разности. di = [ni – n´i] Результаты записаны в таблицу 2, графа 7. N´ = 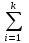 n´i = 39,6 n´i = 39,6λk = 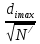 = 0,444 = 0,444По таблице значений P(λk) критерия Колмогорова вероятность P(λk) = 0,9893. Полученное значение близко к единице, что подтверждает правильность выбранного теоретического закона распределения. Таблица 2
3. По критерию χ2 (хи-квадрат). Определяется количество отказов в интервалах отказов по экспериментальным и теоретическим данным. 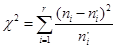 χ2 = 5,59 Число степеней свободы k по формуле: k = r – m – 1 = 10 – 2 – 3 = 7 где r = 10 - количество интервалов, m = 2 - количество параметров закона распределения. По таблице значений - χ2, в зависимости отk иРзначение вероятности Р = 0,5905, что свидетельствует о том, что принятый закон распределения соответствует статистическим данным, т.к. выполнено условие 0,7 ˃Р = 0,5905 ˃ 0,2. 1.5. Определение статистических и теоретических значений вероятности безотказной работы P (x), отказа Q (x), частоты отказов a (x) и интенсивности отказов λ (x) для массива однородных случайных величин Расчёт статистических данных: Вероятность отказа на отрезке времени: QS = mi + mi+1, где mi– частости i-ого интервала. Вероятность безотказной работы: PS = 1 - QS Частота отказов: aS = ni / (N*Δt), где N = 40 – общее число значений, N; Δt = 67 – интервал. Интенсивность отказов: λS = aS / PS Расчет теоретических данных: Вероятность безотказной работы: P(t) = (N – n’(t) / N Вероятность отказа на отрезке времени от 0 до t: Q(t) = 1 – Pt Частота отказов: a(t) = n’i / (N* Δt) Интенсивность отказов: λ(t) = at / Pt Результаты расчётов занесены в таблицу3. Таблица 3
Результаты расчётов позволяют графически согласовать параметрыQ, P, aи λ, определённые на основании статистических данных и принятого закона распределения. Графики параметровQ, P, a и λ, построенные по статистическим (красным) и теоретическим (синим) данным для выбранного закона распределения случайных величин (в примере закон Вейбулла). 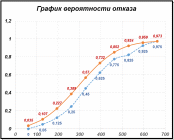 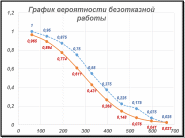 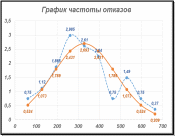 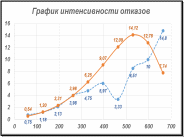 ЗаключениеВ заключении хочется ещё раз отметить исключительно важное значение рассматриваемых в задании вопросов мониторинга надёжности технически сложного оборудования ПДК. Континентальный шельф Российской Федерации является самым крупным в мире по площади. Основная роль в добыче углеводородов при этом принадлежит арктическим (70 % общих ресурсов) и дальневосточным (20 % общих ресурсов) морям. Среди объектов обустройства морских месторождений особое место занимают подводные трубопроводы и оборудование подводных добычных комплексов, эксплуатация которых происходит зачастую в сложных инженерно-геологических и природно-климатических условиях, причем с ограниченными возможностями проведения диагностических и ремонтных работ. По результатам анализа данных по инцидентам и авариям в системах подводных морских комплексах разрабатываются и принимаются технические решения по обеспечению безопасности, а также соответствующие методы контроля и мониторинга для континентального шельфа России. При обосновании показателей рисков эксплуатации ПДК, моделирование последствий аварий является одним из наиболее значимых этапов. Для решения задач, связанных с анализом данных при наличии случайных и непредсказуемых воздействий, разработаны методы математической статистики для анализа данных. Эти методы позволяют выявить закономерности на фоне случайностей, делать обоснованные выводы и прогнозы, давать оценки вероятностей их выполнения или невыполнения. Решение именно этого задания – произвести статистическую обработку массива однородных экспериментальных данных об отказах объекта. состоит в том, чтобы изучить основные понятия математической статистики и применить их к анализу полученных исходных данных. Для решения выполнены: - Предварительная обработка и обобщение статистических данных, построена гистограмма и ломаная – полигон частоты отказов; - Проверка соответствия выбранного закона распределения случайных величин имеющимся статистическим данным. Для выбора рассмотрены способы: графический, по критерию Колмогорова, по критерию χ2 (хи-квадрат). Построен график по теоретическим значениям функции плотности распределения отказов; - Определение статистических и теоретических значений вероятности безотказной работы P (x), вероятности отказа Q (x), частоты отказов a (x) и интенсивности отказов λ (x) для массива однородных случайных величин. Построены соответственно графики. Сделан вывод о соответствии принятого закона распределения статистическим данным. Список информационных источников1. Половко, А. М. Сборник задач по теории надежности / А. М. Половко, И. М. Маликов, А. Н. Жигарев, В. И. Зарудный; под ред. А. М. Половко, И. М. Маликова. – М.: Сов. радио, 1972 – 408 с. 2 Ямпурин, Н. П. Основы надежности электронных средств: учебноепособие для студ. высш. учеб. заведений / Н. П. Ямпурин, А. В. Баранова; под ред. Н. П. Ямпурина. – М.: Издательский центр «Академия», 2010 – 240 с. 3 Липатов, И. Н. Учебное пособие «Решение задач по прикладной теории надежности» / И. Н. Липатов. – Пермь, 1996 – 83 с. 4. Захаров И. В., аспирант РГУ нефти и газа им. И.М. Губкина (г. Москва) /Применение подводных добычных систем при освоении континентального шельфа России /статья/ Электронный ресурс: esa-conference.ru 5. Лисунов, Е.А. Практикум по надежности технических систем [Электронный ресурс]: учеб. пособие. – Электрон. дан. – Санкт-Петербург: 2015. 6. Колде, Я. К. Практикум по теории вероятностей и математической статистике / Я. К. Колде. – М.: Высш. школа, 1991 7. Колемаев, В. А. Теория вероятностей и математическая статистика / В. А. Колемаев, В. Н. Калинина. – М.: Индгра, 1997, | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
