Главная страница
Навигация по странице:

  • Предварительные сведения

  • Описание интерфейса программы

    		•

    курсовая КГ. Курсовая работа. Движение луча света по поверхности Безье


    Скачать 1.3 Mb.
    НазваниеКурсовая работа. Движение луча света по поверхности Безье
    Дата09.01.2022
    Размер1.3 Mb.
    Формат файлаdoc
    Имя файлакурсовая КГ.doc
    ТипКурсовая
    #326428

    Курсовая работа.

    Движение луча света по поверхности Безье

    Цель работы: Изучить представление в компьютерной графике математические модели трехмерных поверхностей, в частности, поверхностей Безье, и способов их визуализации.
    Задание на курсовую работу: разработать программу, осуществляющую имитацию движения луча по поверхности Безье. Программа должна обладать дружественным интерфейсом и предоставлять пользователю возможность влиять на свойства поверхности и луча.
    Предварительные сведения

    Практическое использование в различных областях науки и техники различных типов поверхностей, таких как бикубическая поверхность Кунса или кубических сплайновых кривых затрудняется необходимостью задания точной, интуитивно неочевидной математической информации, например, координат точек, касательных векторов и векторов кручения. Большинство этих проблем можно преодолеть, если использовать математический аппарат поверхностей Безье.

    Поверхности Безье являются обобщением понятии кривых Безье к трехмерному случаю. Декартово или тензорное произведение поверхностей Безье задается в виде:

    , где К и J есть базисные функции Бернштейна в параметрических направлениях u и w: , , а элементы Bij являются вершинами задающей полигональной сетки. Индексы n и m на единицу меньше числа многогранников в направлениях u и w соответственно.

    Из-за того, что для смешивающих функций используется базис Бернштейна, многие свойства поверхности известны:

    • Степень поверхности в каждом параметрическом направлении на единицу меньше числа вершин задающего многоугольника в этом направлении.

    • Гладкость поверхности в каждом параметрическом направлении на 2 единицы меньше числа вершин задающего многоугольника в этом направлении

    • Поверхность отображает в общем виде форму задающей полигональной сетки

    • Совпадают только угловые точки задающей полигональной сетки и поверхности

    • Поверхность содержится внутри выпуклой оболочки задающей полигональной сетки.

    • Поверхность инварианта относительно аффинного преобразования

    • Каждая из граничных линий поверхности Безье является кривой Безье.

    В матричном виде декартово произведение поверхности Безье задается преобразованием :

    Здесь U = [un, un-1, … u1, 1]

    W = [wn, wn-1, …w1, 1]T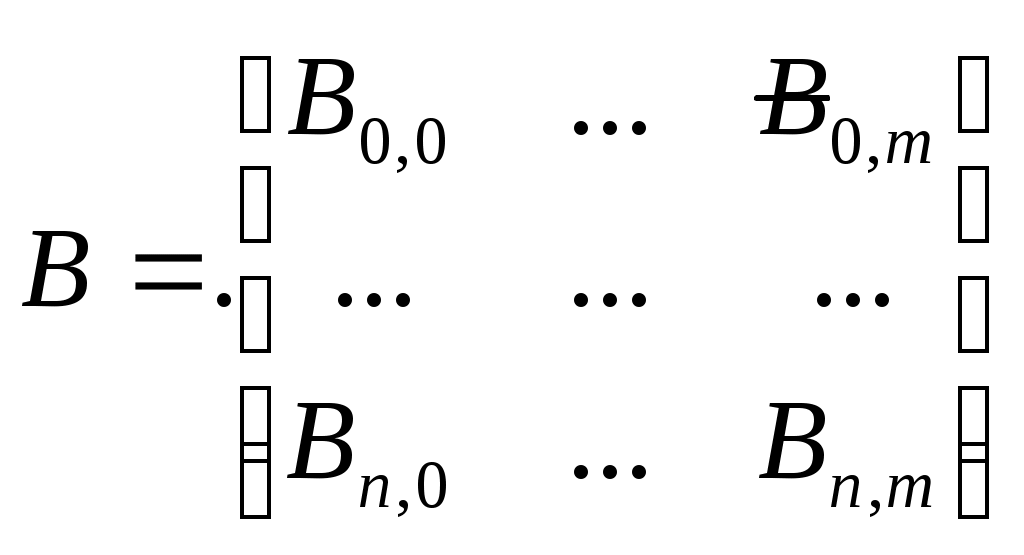

    , N и M вычисляются по формулам



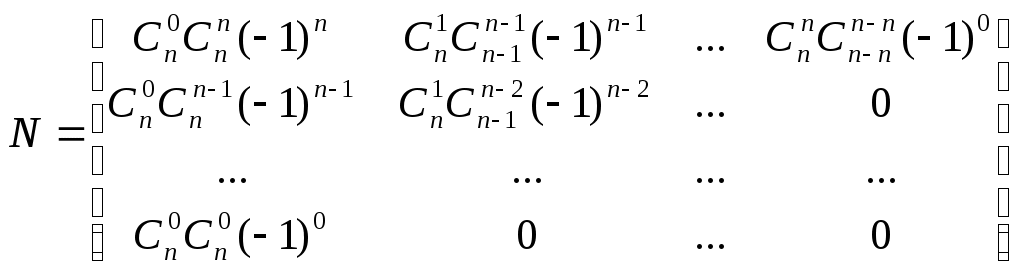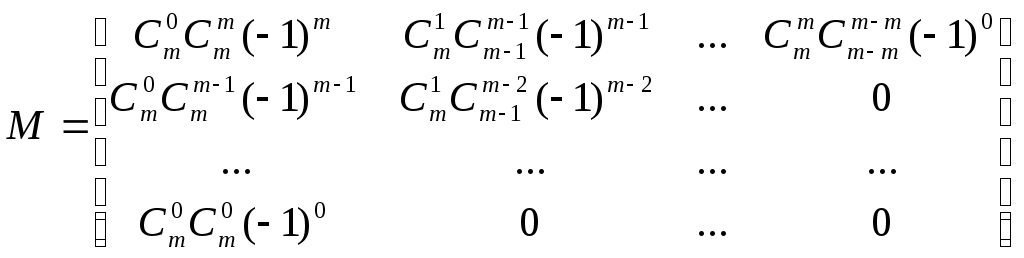    Для специального случая бикубической поверхности Безье размера 4*4 уравнение сокращается до: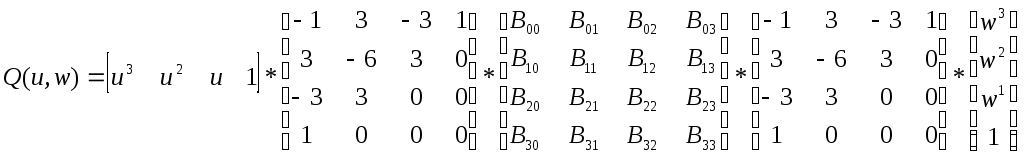



    Поверхность Безье не обязательно должна быть квадратной. Для сетки размера 5*3 уравнение превращается в: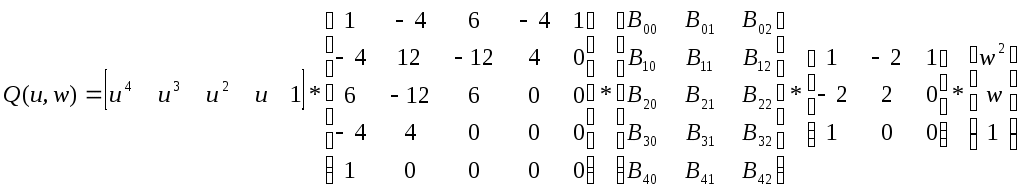

    На рисунке 1 представлена бикубическая поверхность Безье, на рисунке 2 – поверхность 5*3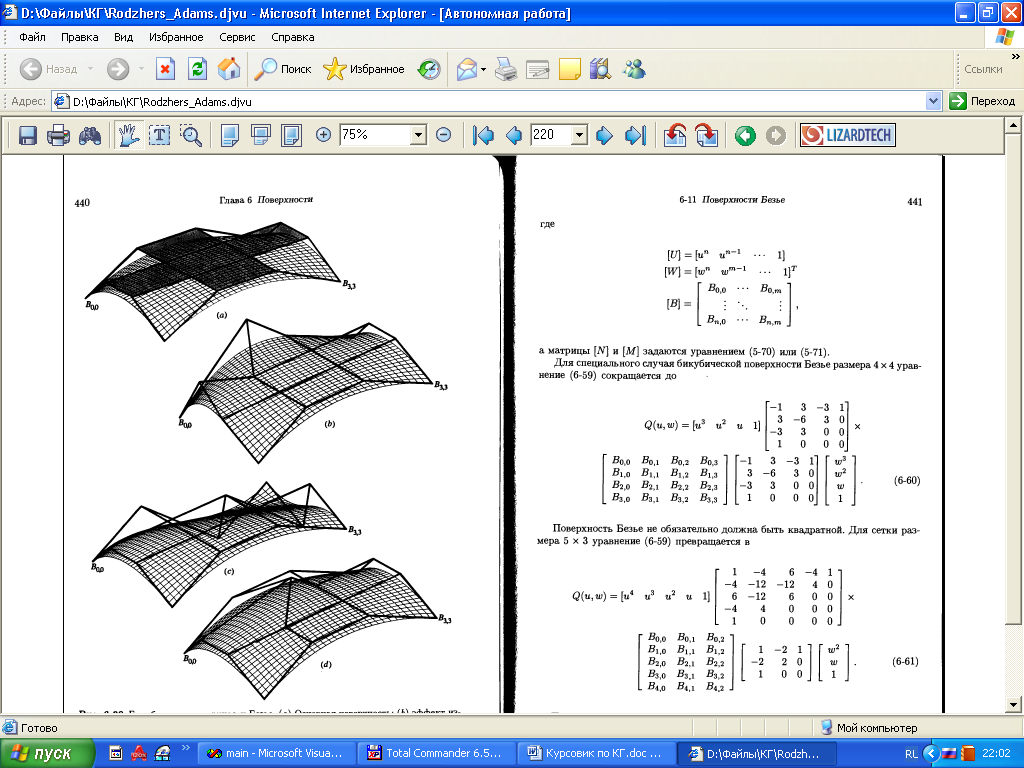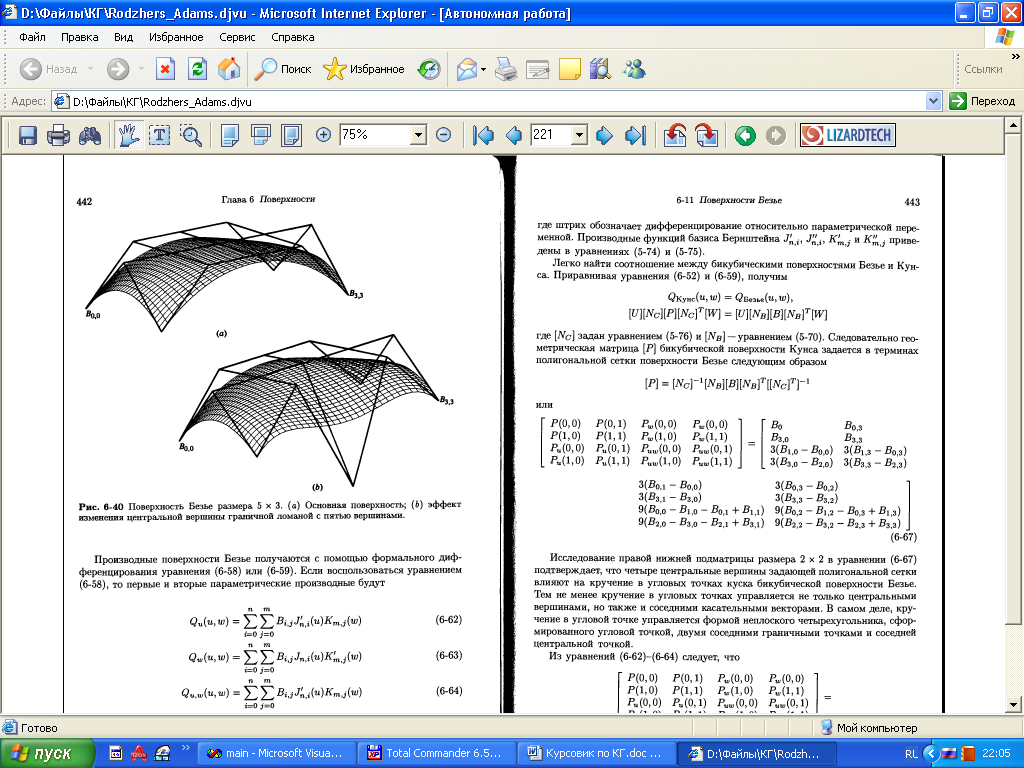



    Рисунок 1 Рисунок 2
    Поверхности Безье связаны со многими другими геометрическими моделями, например, поверхностями Кунса, рассмотрение которых остается за пределами данной работы.
    Описание интерфейса программы.

    Программа с помощью матричных преобразований создает и визуализирует поверхность Безье на основе полигональной сетки. Пользователю предоставляется возможность совершать следующие действия с помощью клавиатуры:

    • Перемещение поверхности в пространстве (клавиши ‘a’ и ‘d’ – вправо-влево, ‘w’ и ‘s’ – вверх-вниз, ‘e’и ‘r’ – вперед-назад).

    • Визуализация каркасной сетки поверхности и непрерывного изображения, переключение между ними (клавиша ‘l’)

    • Включение \ выключение источника света (клавиша ‘p’)

    • Увеличение \ уменьшение количества полигональных узлов базисной сетки:(клавиши ‘n’ и ‘m’ в одном направлении, клавиши ‘h’ и ‘j’ – в другом направлении).

    • Выбор цвета источника света:

      • Клавиша ‘1’ – красный

      • Клавиша ‘2’ – зеленый

      • Клавиша ‘3’ – синий

      • Клавиша ‘4’ – желтый

      • Клавиша ‘5’ – фиолетовый

      • Клавиша ‘6’ – голубой

      • Клавиша ‘7’ – белый

    • Расширение и сужение угла прожектора (клавиши ‘8’ и ‘9’)

    • Увеличение и уменьшение яркости цвета (клавиши ‘+’ и ‘-’)

    • Увеличение и уменьшение скорости вращения (клавиши ‘f’ и ‘F’)

    • Поворот оси вращения (клавиши ‘x’ и ‘X’ изменяют наклон оси вращения относительно оси абсцисс, ‘y’ и ‘Y’ – относительно оси ординат, ‘z’ и ‘Z’ – относительно оси апликат).



    Примеры изображения каркасной сетки поверхности Безье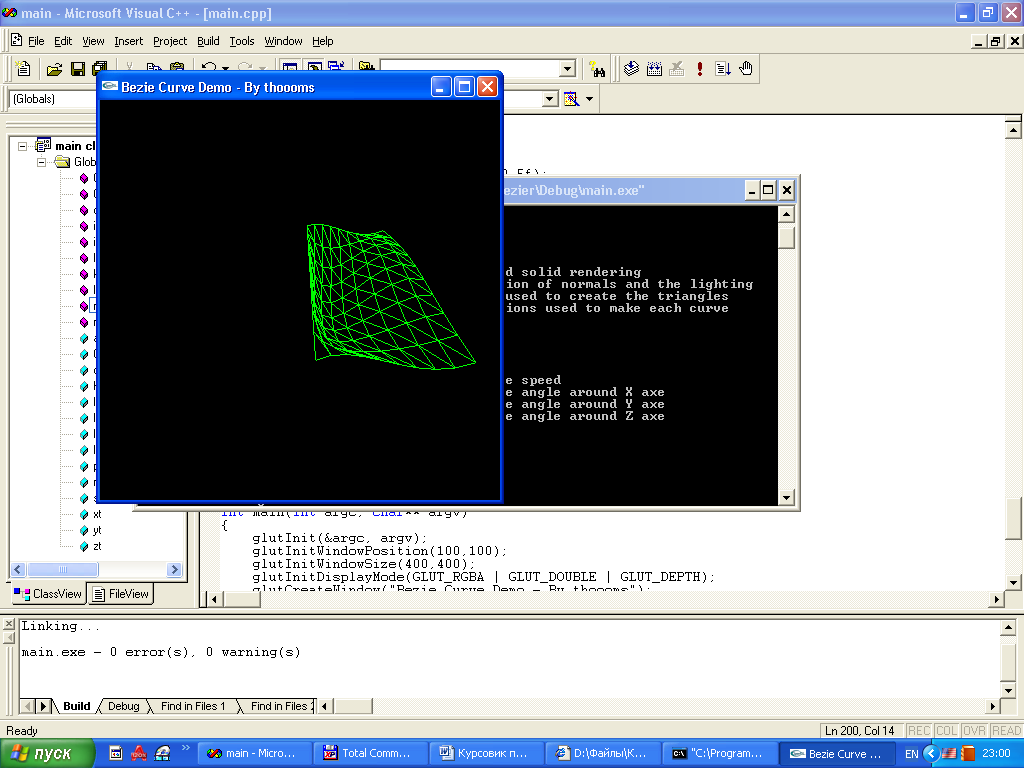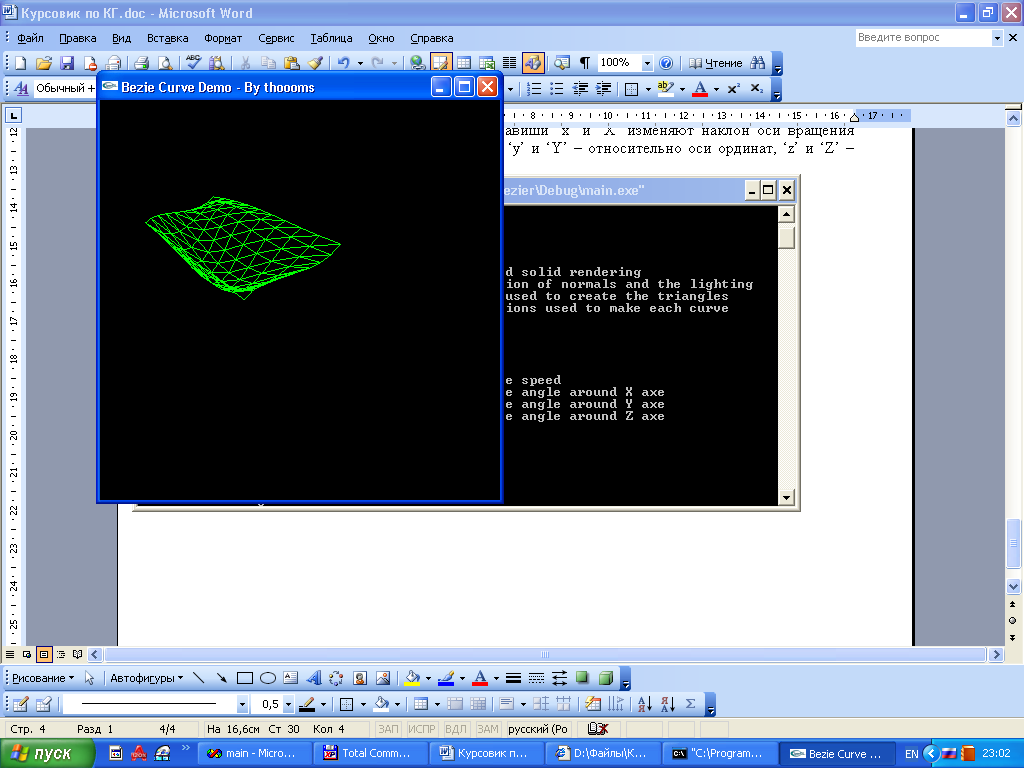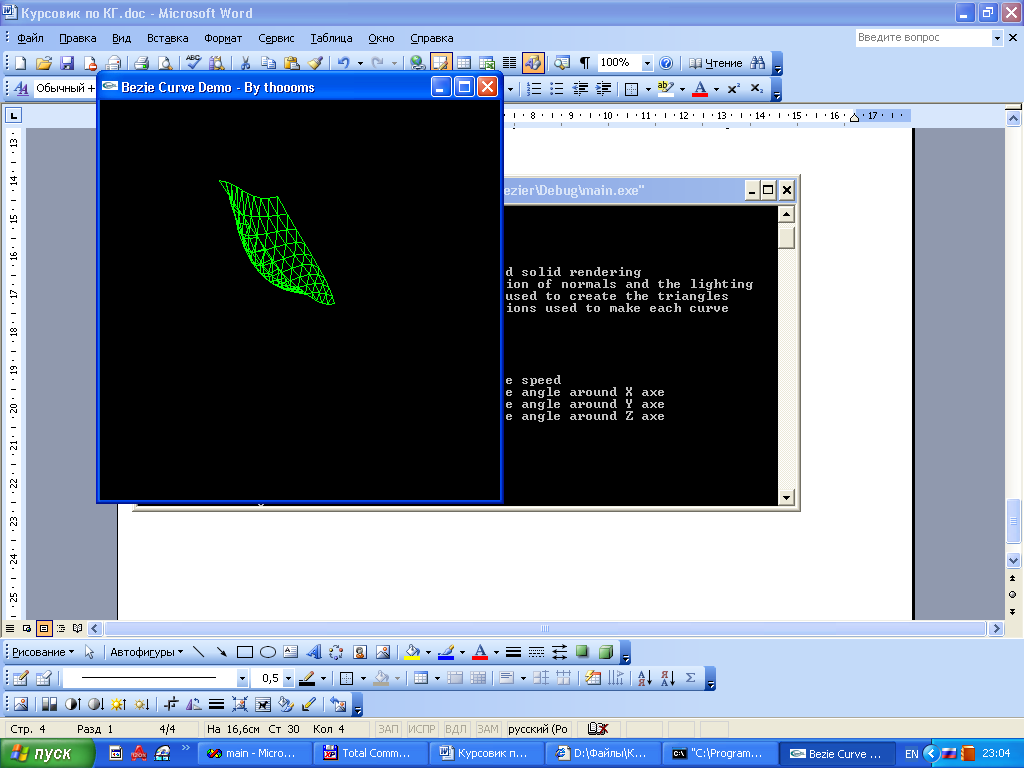



    Примеры изображения луча разных цветов и плсщади на поверхности Безье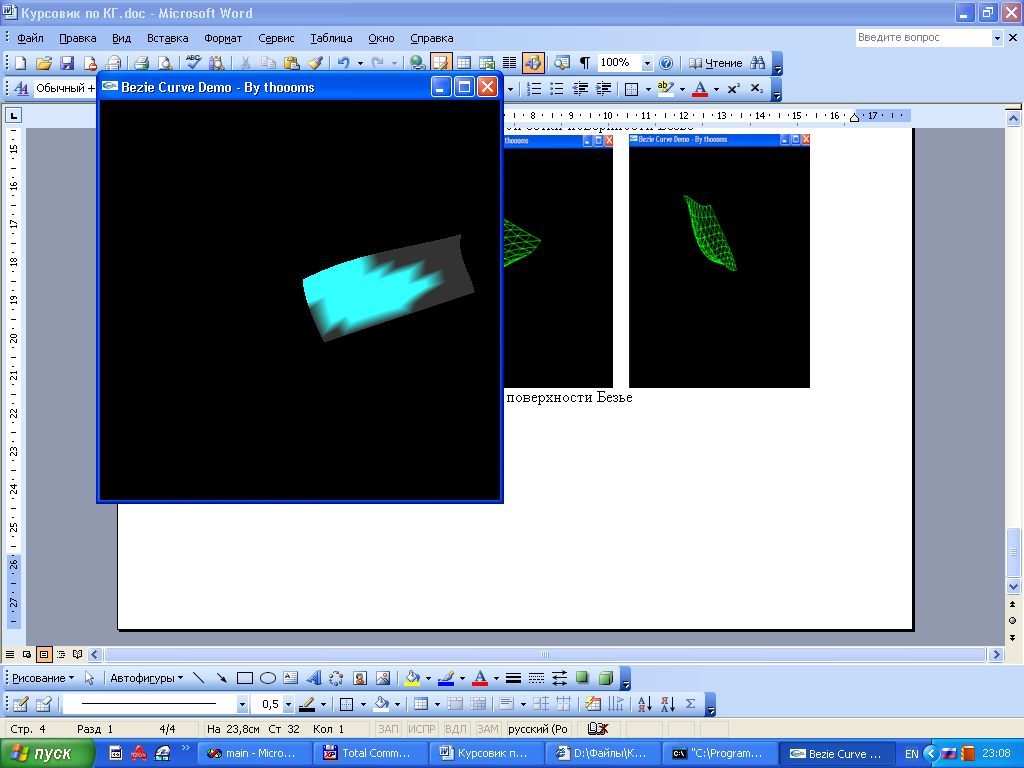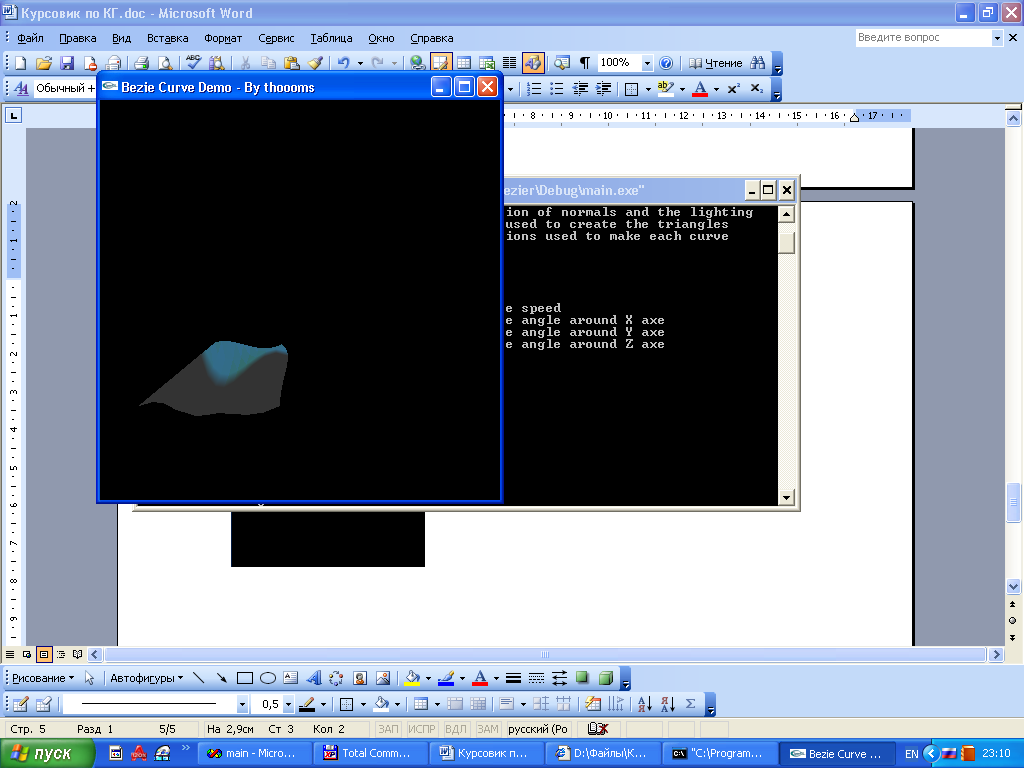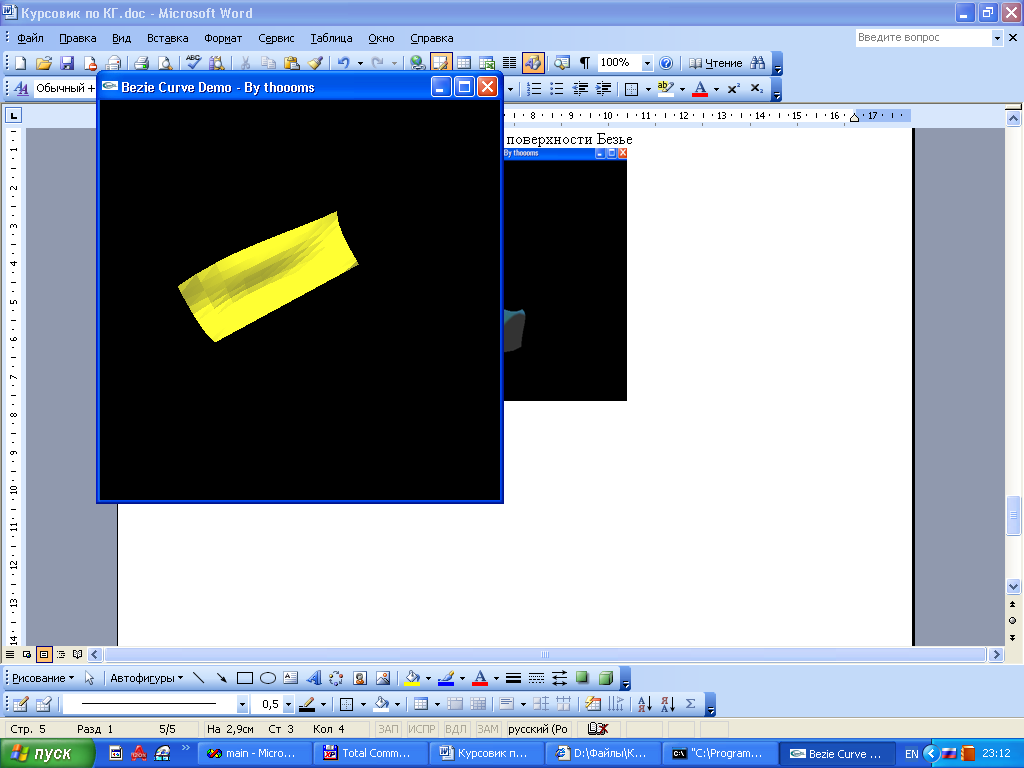


    Поверхность Безье: измененная полигональная сетка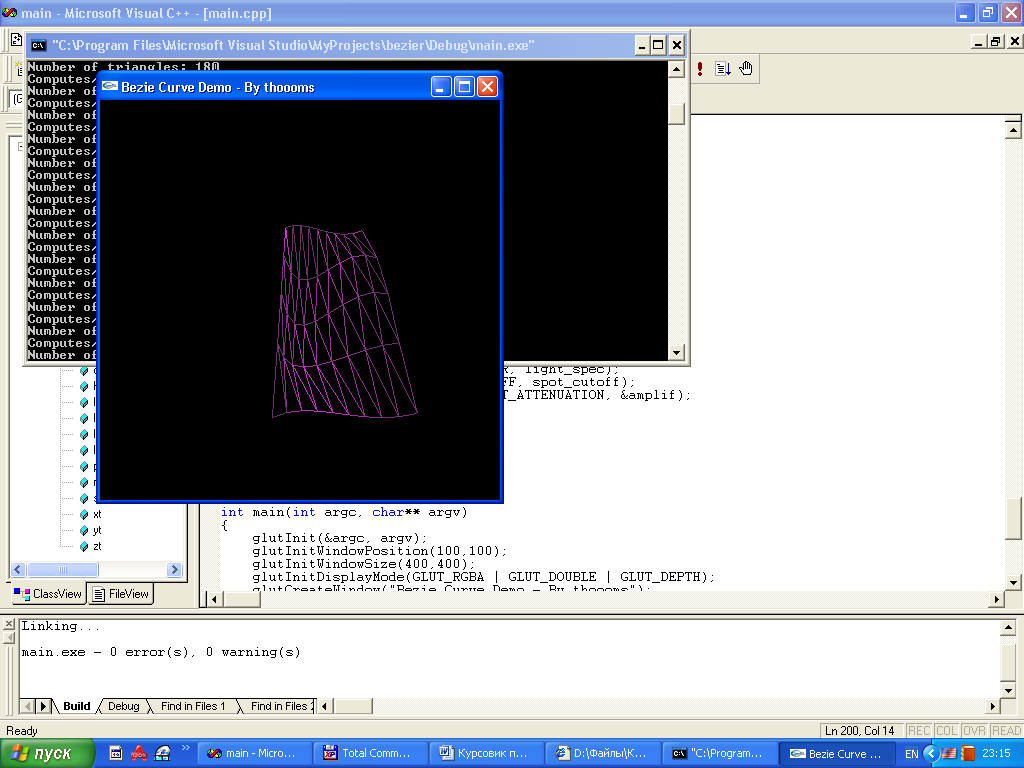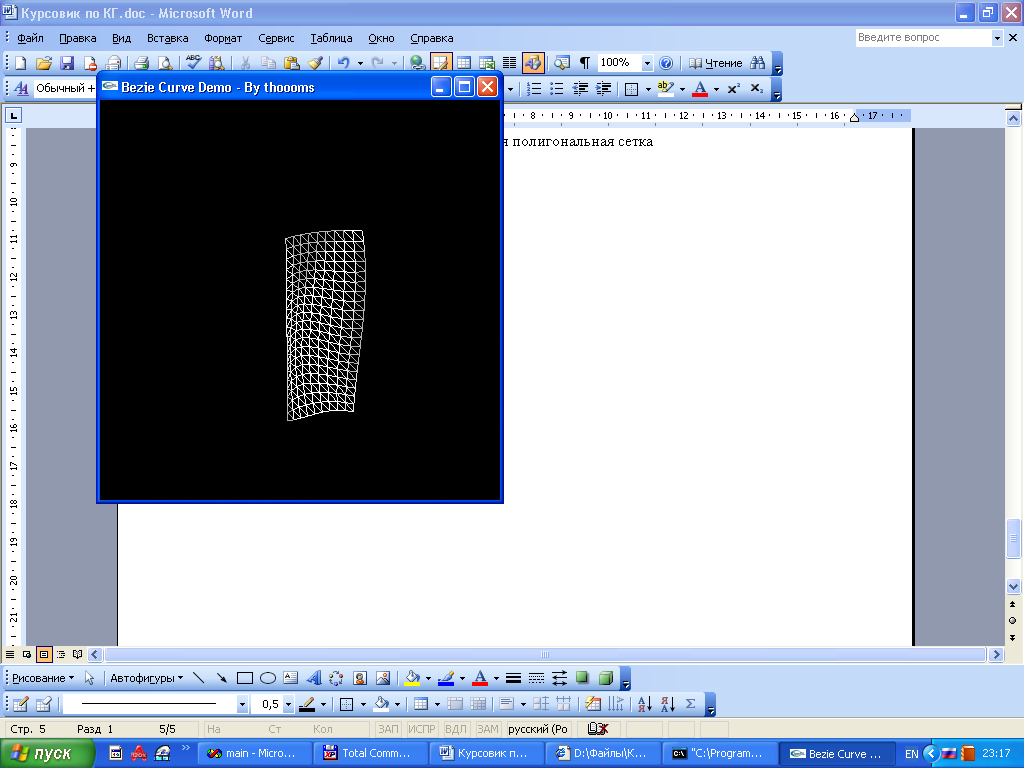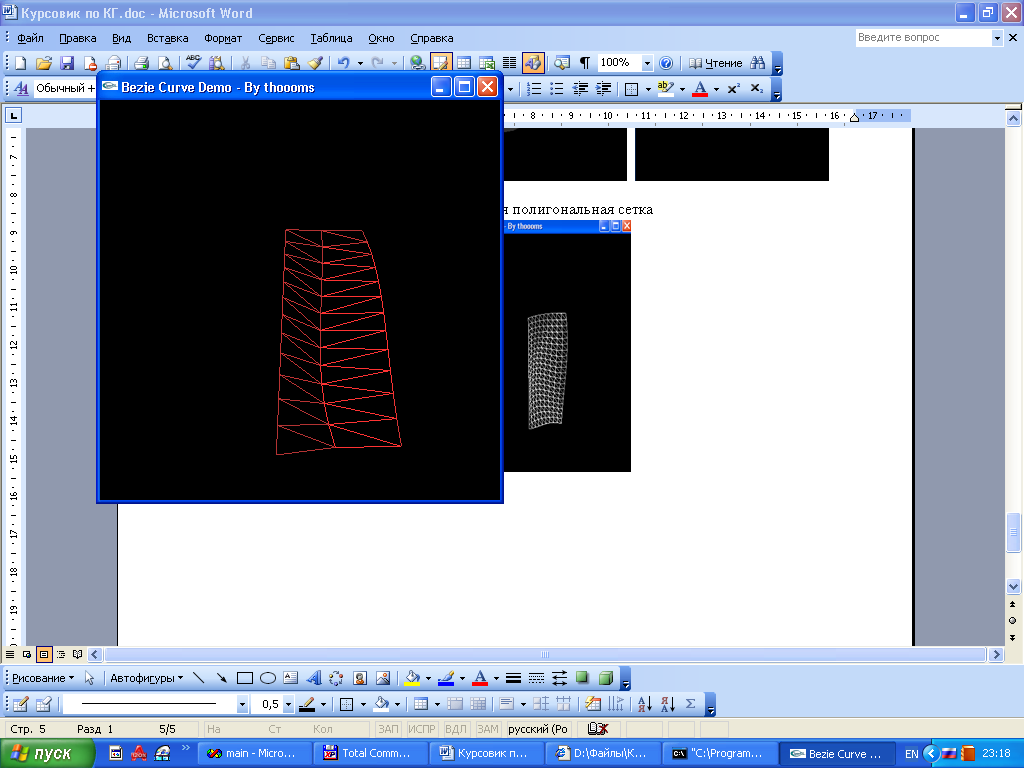



    Пояснение пользователю




    Приложение

    Текст программы на языке С++ с использованием библиотеки OpenGL

    #include "windows.h"

    #include

    #include "matrix.h"

    #include "curves.h"

    #include "stdio.h"
    float xt = 0.0f;

    float yt = 0.0f;

    float zt = 0.0f;

    float h = 1.0f;
    GLfloat light_amb[] = {0.0f, 1.0f, 0.4f, 1.0f};

    GLfloat light_diff[] = {0.0f, 0.0f, 0.3f, 1.0f};

    GLfloat light_spec[] = {0.3f, 0.8f, 0.3f, 0.5f};

    GLfloat light_pos[] = {0,0,0,1};
    float amplif = 1.0; //light amplification

    float spot_cutoff = 180; //light spot cutoff
    float rotatus[] = {1.0, 0.0, 0.0};
    //create control point for patch

    Point CP[16];
    CCubicCurve curves[4]; //four curves

    CCubicPatch patch;
    void InitCurves()

    {

    CP[0].x = 1.0f;

    CP[0].y = 1.0f;

    CP[0].z = 1.0f;

    CP[1].x = 4.0f;

    CP[1].y = 2.0f;

    CP[1].z = 0.0f;

    CP[2].x = 8.0f;

    CP[2].y =-2.0f;

    CP[2].z = 0.0f;

    CP[3].x = 12.0f;

    CP[3].y = 0.0f;

    CP[3].z = 0.0f;
    CP[4] = CP[0];

    CP[4].z += 10.0f;
    CP[5] = CP[1];

    CP[5].y = -20.0f;

    CP[5].z += 10.0f;

    CP[6] = CP[2];

    CP[6].y = 10.0f;

    CP[6].z += 10.0f;

    CP[7] = CP[3];

    CP[7].z += 10.0f;

    CP[7].x += 2.0f;
    CP[8] = CP[0];

    CP[8].z += 20.0f;
    CP[9] = CP[1];

    CP[9].y += -15.0f;

    CP[9].x = -1.0f;

    CP[9].z += 20.0f;

    CP[10] = CP[2];

    CP[10].z += 20.0f;

    CP[11] = CP[3];

    CP[11].z += 20.0f;

    CP[12] = CP[0];

    CP[12].z += 30.0f;
    CP[13] = CP[1];

    CP[13].z += 30.0f;

    CP[14] = CP[2];

    CP[14].z += 30.0f;

    CP[15] = CP[3];

    CP[15].z += 30.0f;

    patch.GeneratePatch(CP);
    Matrix4x1 p1, p2, p3, p4;

    p1.M[0] = -7.0f;

    p1.M[1] = 2.0f;

    p1.M[2] = 0.0f;
    p2.M[0] = -7.0f;

    p2.M[1] = 2.0f;

    p2.M[2] = 2.0f;
    p3.M[0] = -7.0f;

    p3.M[1] = 2.0f;

    p3.M[2] = 3.0f;
    p4.M[0] = -7.0f;

    p4.M[1] = 2.0f;

    p4.M[2] = 4.0f;
    curves[0].GenerateBezierCoefficients(p1,p2,p3,p4);
    //subdivide curve

    curves[0].SubdivideBezierCurve(&curves[1], &curves[2]);
    //give subdiveded curves another color

    curves[1].SetColor(1,0,0,0.5f);

    curves[2].SetColor(0,1,0,0.5f);
    curves[1].SubdivideBezierCurve(&curves[0], &curves[3]);

    curves[0].SetColor(1,1,1,0.5f);

    curves[3].SetColor(1,1,0,0.5f);

    }
    void lightcolor(float R = 0.0f, float G = 0.0f, float B = 0.0f)

    {

    if (R > 1.0 || R < 0.0 || G > 1.0 || G < 0.0 || B > 1.0 || B < 0.0)

    return;

    light_amb[0] = R;

    light_amb[1] = G;

    light_amb[2] = B;

    light_diff[0] = R;

    light_diff[1] = G;

    light_diff[2] = B;

    glLightfv(GL_LIGHT0, GL_AMBIENT, light_amb);

    glLightfv(GL_LIGHT0, GL_DIFFUSE, light_diff);

    }
    void reshape(int w, int h)

    {

    glViewport(0,0,w,h);

    glMatrixMode(GL_PROJECTION);

    glLoadIdentity();

    gluPerspective(60, 1, 0.1, 200);

    glMatrixMode(GL_MODELVIEW);

    glLoadIdentity();

    gluLookAt(0,-10,50, 0,-10,0, 0,1,0);

    glLightfv(GL_LIGHT0, GL_POSITION, light_pos);

    }
    void keyboard(unsigned char key, int x, int y)

    {

    static bool line_on = false;

    switch (key)

    {

    case 'l':

    if (line_on)

    glPolygonMode(GL_FRONT_AND_BACK, GL_FILL);

    else

    glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);
    line_on = !line_on;

    break;

    case 'a':

    xt -= 1.0f;

    break;

    case 'd':

    xt += 1.0f;

    break;

    case 'w':

    yt +=1.0f;

    break;

    case 's':

    yt -=1.0f;

    break;

    case 'e':

    zt -= 1.0f;

    break;

    case 'r':

    zt += 1.0f;

    break;

    case 'n':

    patch.ChangeEval(TM_S_EVALS, -1);

    break;

    case 'm':

    patch.ChangeEval(TM_S_EVALS, 1);

    break;

    case 'h':

    patch.ChangeEval(TM_CURVE_EVALS, -1);

    break;

    case 'j':

    patch.ChangeEval(TM_CURVE_EVALS, 1);

    break;

    case 'p':

    {

    static bool light = false;

    if (light)

    glDisable(GL_LIGHTING);

    else

    glEnable(GL_LIGHTING);

    patch.ToggleNormals();

    light = !light;

    }break;

    case '1':

    { lightcolor(1, 0, 0); break;}

    case '2':

    { lightcolor(0, 1, 0); break;}

    case '3':

    { lightcolor(0, 0, 1); break;}

    case '4':

    { lightcolor(1, 1, 0); break;}

    case '5':

    { lightcolor(1, 0, 1); break;}

    case '6':

    { lightcolor(0, 1, 1); break;}

    case '7':

    { lightcolor(1, 1, 1); break;}

    case '8':

    {

    spot_cutoff -= 10;

    glLightf(GL_LIGHT0,GL_SPOT_CUTOFF, spot_cutoff);

    break;

    }

    case '9':

    {

    spot_cutoff += 10;

    glLightf(GL_LIGHT0,GL_SPOT_CUTOFF, spot_cutoff);

    break;

    }

    case '+':

    {

    amplif -= 0.1;

    glLightfv(GL_LIGHT0, GL_CONSTANT_ATTENUATION, &lif);

    break;

    }

    case '-':

    {

    amplif += 0.1;

    glLightfv(GL_LIGHT0, GL_CONSTANT_ATTENUATION, &lif);

    break;

    }

    case 'f':{h = h*2; break;}

    case 'F':{h = h/2.0; break;}

    case 'x':

    {

    if (rotatus[0] < 1)

    rotatus[0] += 0.1f;

    break;

    }

    case 'X':

    {

    if(rotatus[0] > 0)

    rotatus[0] -= 0.1f;

    break;

    }

    case 'y':

    {

    if (rotatus[1] < 1)

    rotatus[1] += 0.1f;

    break;

    }

    case 'Y':

    {

    if (rotatus[1] > 0)

    rotatus[1] -= 0.1f;

    break;

    }

    case 'z':

    {

    if (rotatus[2] < 1)

    rotatus[2] += 0.1f;

    break;

    }

    case 'Z':

    {

    if (rotatus[2] > 0)

    rotatus[1] -= 0.1f;

    break;

    }

    case 27:

    exit(0);

    break;

    default:

    break;

    }

    glutPostRedisplay();

    }
    void display()

    {

    static float rot = 0;

    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

    glPushMatrix();
    //allow the user to move the patch for further examination

    glTranslatef(-xt, -yt, -zt);

    glRotatef(rot, rotatus[0], rotatus[1], rotatus[2]);

    patch.Draw();

    glPopMatrix();

    glFlush();

    glutSwapBuffers();
    if (rot >= 360.0f)

    rot -= 360.0f;

    rot += h;

    }
    void init()

    {

    glClearColor(0.0f, 0.0f, 0.0f, 0.5f);

    glEnable(GL_DEPTH_TEST);

    glColor3f(0,1,0);

    glLineWidth(1);

    InitCurves();
    glDisable(GL_LIGHTING); //is turned on by the user

    glEnable(GL_LIGHT0);
    GLfloat amb[] = {1,1,1,0.5f};

    glLightModelfv(GL_LIGHT_MODEL_AMBIENT, amb);
    //init lights

    glLightfv(GL_LIGHT0, GL_AMBIENT, light_amb);

    glLightfv(GL_LIGHT0, GL_DIFFUSE, light_diff);

    glLightfv(GL_LIGHT0, GL_SPECULAR, light_spec);

    glLightf(GL_LIGHT0,GL_SPOT_CUTOFF, spot_cutoff);

    glLightfv(GL_LIGHT0, GL_CONSTANT_ATTENUATION, &lif);
    }
    void idle()

    {

    glutPostRedisplay();

    }
    int main(int argc, char** argv)

    {

    glutInit(&argc, argv);

    glutInitWindowPosition(100,100);

    glutInitWindowSize(400,400);

    glutInitDisplayMode(GLUT_RGBA | GLUT_DOUBLE | GLUT_DEPTH);

    glutCreateWindow("Bezie Curve Demo - By thoooms");
    printf("\n\n\n-------------\nBezie Curve Demo - \n-------------");

    printf("\n'a' and 'd':\t x axis movement");

    printf("\n'w' and 's':\t y axis movement");

    printf("\n'e' and 'r':\t z axis movement");

    printf("\n'l':\t\t switches between wireframe and solid rendering");

    printf("\n'p':\t\t Enables/Disables the calculation of normals and the lighting");

    printf("\n'n' and 'm':\t Changes the number of curves used to create the triangles");

    printf("\n'h' and 'j':\t Changes the number of evaluations used to make each curve");

    printf("\n'1' - '7' :\t Light an object a color");

    printf("\n'8':\t : Cut off the entrance angle");

    printf("\n'9':\t : Extend tht entrance angle");

    printf("\n'+':\t : Add the brightness");

    printf("\n'-':\t : Delete the brightness");

    printf("\n'f' and 'F':\t Increase and decrease a rotate speed");

    printf("\n'x' and 'X':\t Increase and decrease a rotate angle around X axe");

    printf("\n'y' and 'Y':\t Increase and decrease a rotate angle around Y axe");

    printf("\n'z' and 'Z':\t Increase and decrease a rotate angle around Z axe");

    init();
    glutDisplayFunc(display);

    glutKeyboardFunc(keyboard);

    glutReshapeFunc(reshape);

    glutIdleFunc(idle);

    glutMainLoop();
    return 0;

    }
    Выводы: В процессе выполнения курсовой работы были освоены навыки в представлении полигональных моделей, в частности, поверхностей Безье для аппроксимации и визуализации трехмерных поверхностей.
    Список использованных источников

    1. Д.Роджерс, Дж.Адамс. Математические основы машинной графики, Москва, «Мир», 2001г.

    2. Ресурсы сайта alglib.source.ru

    написать администратору сайта