Гидравлика курсовая работа. курсач. Курсовая работа Гидравлический расчет сложного трубопровода и элементов оборудования по дисциплине Гидравлика и нефтегазовая гидромехпника
 Скачать 189.47 Kb. Скачать 189.47 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Уфимский государственный нефтяной технический университет» Кафедра «Гидрогазодинамика трубопроводных систем и гидромашины» КУРСОВАЯ РАБОТА «Гидравлический расчет сложного трубопровода и элементов оборудования» по дисциплине «Гидравлика и нефтегазовая гидромехпника» Выполнил Студент группы ФИО Проверил Доцент, к.т.н. ФИО Уфа 2022 2 Гидравлический расчет разветвленного трубопровода Выполнить гидравлический расчет разветвленного трубопровода, схема которого прилагается. 1) Определить Pвх и d3, d4 из условия, что Q3=Q4 2) Выполнить гидравлический расчет (комплексная задача) разветвленного трубопровода, схема которого прилагается. а) Как изменятся расходы при увеличении вязкости в 2,5 раза? 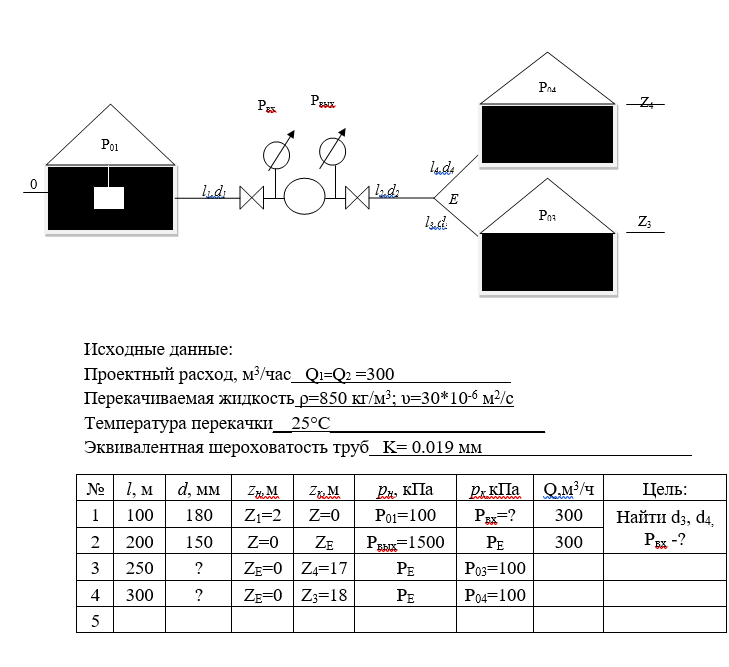 Определение входного давления на насос Данную схему можно разбить на 4 простых трубопровода, причем трубопровод 1 (l1, d1) является всасывающим и рассчитывается отдельно от сложного трубопровода, состоящего из трубы 2 (l2, d2), трубы 3 (l3, d3) и трубы 4 (l4, d4). Составим уравнение Бернулли для трубопровода 1. При этом начальное сечение соответствует свободной поверхности жидкости в первом резервуаре, а конечное сечение – на входе в насос. 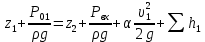 где 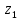 – высотная отметка начального сечения; – высотная отметка начального сечения;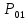 – избыточное давление на свободной поверхности в первом резервуаре; – избыточное давление на свободной поверхности в первом резервуаре;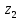 – высотная отметка входа в насос. – высотная отметка входа в насос.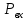 – избыточное давление на входе в насос; – избыточное давление на входе в насос;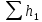 – суммарные потери напора в первом трубопроводе. – суммарные потери напора в первом трубопроводе.Средняя скорость движения жидкости в первом трубопроводе равна: 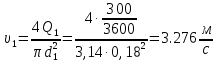 . .Рассчитываем число Рейнольдса: 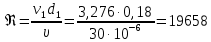 , ,Рассчитываем переходные числа Рейнольдса: 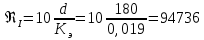 , , 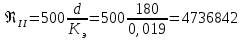 . .Полученное число Рейнольдса меньше ReI из чего следует, что в первом трубопроводе турбулентный режим течения, зона гидравлического трения. Коэффициент Кориолиса для инженерных расчетов можно принять равным единице. Коэффициент гидравлического сопротивления 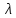 определяем по формуле Блазиуса: определяем по формуле Блазиуса: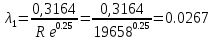 . .Рассчитываем суммарные потери напора во втором трубопроводе: 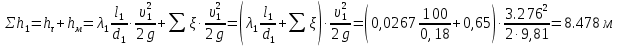 , ,где 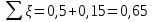 (вход в трубу, полностью открытая задвижка). (вход в трубу, полностью открытая задвижка).Из уравнения Бернулли определяем 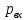 : :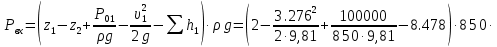 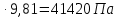 . .Определение потерей напора в 3 и 4 трубопроводе. Составим систему уравнений Бернулли для разветвленной части трубопроводной сети. Для трубопровода 2: 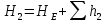 , ,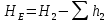 , ,Для трубопровода 3: 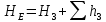 , ,Для трубопровода 4: 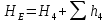 , ,Где 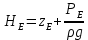 ; ;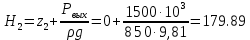 м; м;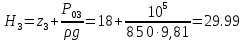 м; м;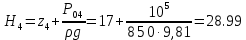 м. м.Уравнения расходов: Q1 = Q2 = Q Q = Q3 + Q4  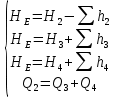 Средняя скорость жидкости в трубопроводе 2 равна: 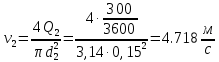 Рассчитываем число Рейнольдса: Рассчитываем число Рейнольдса: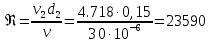 Рассчитываем переходные числа Рейнольдса: Рассчитываем переходные числа Рейнольдса: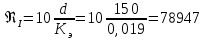 , , 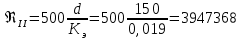 . .Полученное число Рейнольдса меньше ReI из чего следует, что в первом трубопроводе турбулентный режим течения, зона гидравлического трения. Коэффициент Кориолиса для инженерных расчетов можно принять равным единице. Коэффициент гидравлического сопротивления 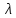 определяем по формуле Блазиуса: определяем по формуле Блазиуса: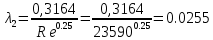 Рассчитываем суммарные потери напора во втором трубопроводе: 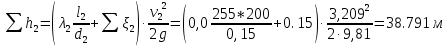 где где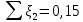 (полностью открытая задвижка). (полностью открытая задвижка).Из уравнения (1) определяем 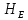 : :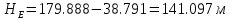 Из уравнений (2) и (3) выражаем суммарные потери напора в третьем и четвертом трубопроводе: Из уравнений (2) и (3) выражаем суммарные потери напора в третьем и четвертом трубопроводе: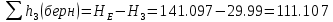 м, м,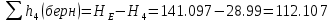 м. м.Найдем диаметры третьего и четвертого трубопроводов. Гидравлическая характеристика трубопровода № 3 При диаметре трубопровода 100 мм: 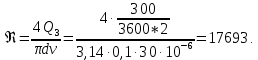 Рассчитываем переходные числа Рейнольдса 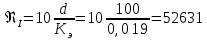 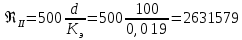 Полученное число Рейнольдса меньше 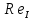 , из чего следует, что в первом трубопроводе турбулентный режим течения, зона гладкого трения. , из чего следует, что в первом трубопроводе турбулентный режим течения, зона гладкого трения.Коэффициент гидравлического сопротивления 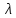 определяем по формуле Блазиуса: определяем по формуле Блазиуса: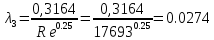 Средняя скорость движения жидкости в трубопроводе равна: 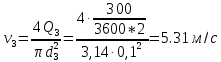 Суммарные потери напора в трубопроводе 3: 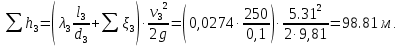 Аналогичные действия выполняются для других диаметров. Таблица 1 – Данные для построения гидравлической характеристики трубопровода № 3
Гидравлическая характеристика трубопровода № 4 будет находиться таким же образом, как и для трубопровода № 3. Таблица 2 – Данные для построения гидравлической характеристики трубопровода № 4
На оси ординат откладываем величины 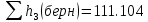 м и м и 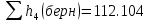 м, и проводя горизонталь до пересечения с построенной кривой Σhi(di), получаем соответствующее значение диаметра (Рисунок 5). м, и проводя горизонталь до пересечения с построенной кривой Σhi(di), получаем соответствующее значение диаметра (Рисунок 5).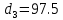 мм, мм, 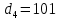 мм, мм,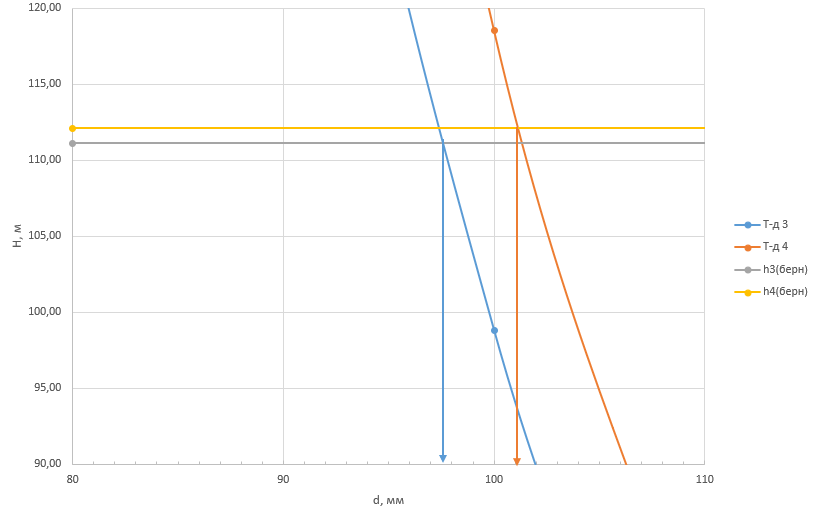 Рисунок 5 – Зависимости потерь напора от диаметра в трубопроводах Рисунок 5 – Зависимости потерь напора от диаметра в трубопроводах№ 3 и № 4 Определение расходов при изменении вязкости в 2.5 раза Проверим зависимость расходов от вязкости, построив гидравлические характеристики труб, по которым течет жидкость с вязкостью в 𝜈/2.5. Новая вязкость примет значение 𝜈 = 12*10-6 м2/c. Будем считать, что давление на выходе из насоса осталось прежним. Составим уравнение Бернулли для трубопроводов 2, 3, 4, относительно плоскости отсчета. При этом начальное сечение трубопровода 2 соответствует выходу из насоса, а конечное сечение – в т.Е. Для трубопроводов 3, 4 начальное сечение находится в т.Е, а конечное сечение – на входе в резервуары 3, 4 соответственно. 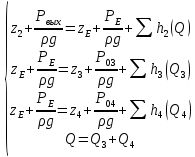 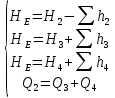 Где 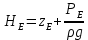 ; ;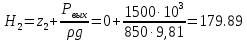 м; м;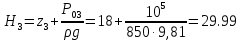 м; м;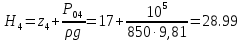 м. м.Для решения полученной системы уравнений рассчитаем гидравлические характеристики каждого трубопровода. Рассчитаем потери напора в каждой из труб по формуле: 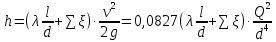 Для каждого значения расхода Q рассчитываем число Рейнольдса: 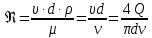 Сравнивая полученное число Рейнольдса с критическим Reкр = 2320 и граничными (переходными) числами 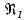 и и 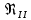 (граничные числа Рейнольдса – ReI и ReII для всех трубопроводов остались прежними (см. задание 2)), определяем режим движения (ламинарный или турбулентный) и, в случае турбулентного режима, зону гидравлического сопротивления (гладких труб, смешанного трения, шероховатых труб). (граничные числа Рейнольдса – ReI и ReII для всех трубопроводов остались прежними (см. задание 2)), определяем режим движения (ламинарный или турбулентный) и, в случае турбулентного режима, зону гидравлического сопротивления (гладких труб, смешанного трения, шероховатых труб).Если число Рейнольдса Re < Reкр=2320, то режим движения ламинарный, и λ определяем по формуле Стокса: 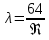 Если 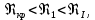 то режим движения турбулентный, зона гладких труб, и λ определяем по формуле Блазиуса: то режим движения турбулентный, зона гладких труб, и λ определяем по формуле Блазиуса: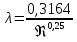 Если 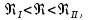 то режим движения турбулентный, зона смешанного трения, и λ определяем по формуле Альтшуля: то режим движения турбулентный, зона смешанного трения, и λ определяем по формуле Альтшуля: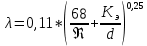 Если 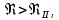 то режим движения турбулентный, зона шероховатого трения, и λ определяем по формуле Шифринсона: то режим движения турбулентный, зона шероховатого трения, и λ определяем по формуле Шифринсона: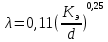 Составим гидравлические характеристики трубопроводов, с учетом зоны трения и расчета коэффициента гидравлических сопротивлений по соответствующим формулам. При средней скорости жидкости в трубопроводе 2 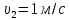 : :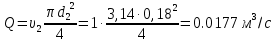 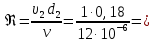 12500 12500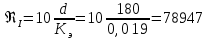 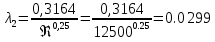 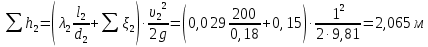 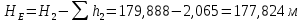 Аналогичные расчеты выполняются при других средних скоростях жидкости в трубопроводе 2. Таблица 3 – Данные для построения гидравлической характеристики трубопровода №2
Гидравлическая характеристика трубопровода № 3 будет находиться таким же образом, как и для трубопровода № 2. Таблица 4 – Данные для построения гидравлической характеристики трубопровода №3
Гидравлическая характеристика трубопровода № 4 будет находиться таким же образом, как и для трубопровода № 3. Таблица 5 – Данные для построения гидравлической характеристики трубопровода №4
Строим графическую зависимость напора от расхода (Рисунок 6). 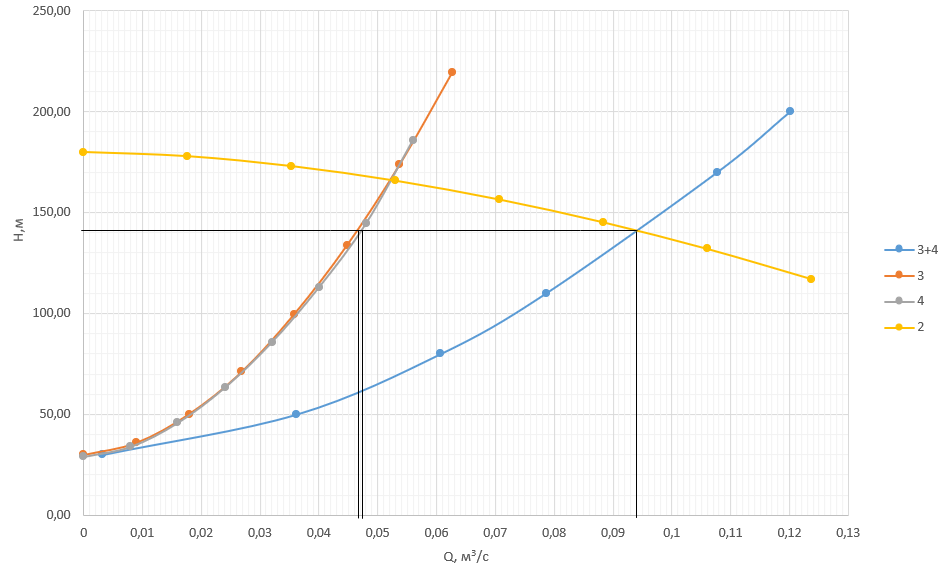 Рисунок 6 – Гидравлические характеристики трубопроводов, по которым течет жидкость вязкостью ν = 12*10-6 м2/с Точка пересечения графиков суммы расходов в трубопроводе №3 и 4 и расхода в трубопроводе №2 будет соответствовать расходу в трубопроводе №2 (по оси х) и напору в т.Е (по оси у). По графику определяем значения расходов Q2, Q3 и Q4. Они соответственно равны Q3=0,0466 м3/с = 167,76 м3/ч, Q4= 0,0474 м3/с = 170,64 м3/ч, Q2= 0,094 м3/с = 338,4 м3/ч. Сделаем вывод, что при уменьшении вязкости расход увеличивается. ВЫВОД В результате выполнения курсовой работы были реализованы следующие компетенции: 1) Способность проводить количественный и качественный анализ параметров и контроль физического, химического, экологического состояния природных и технических механизированных, в том числе автоматизированных, систем и социальных систем(ОПК-1, специальность 21.05.06 «Нефтегазовые техника и технологии»). 2) Способность использовать рациональные методы моделирования процессов природных и технических систем, сплошных и разделенных сред, геологической среды, массива горных пород(ПК-9,специальность 21.05.06 «Нефтегазовые техника и технологии»). 3) способность выбирать и применять соответствующие методы моделирования физических, химических и технологических процессов(ПК-26, направление подготовки 21.03.01 «Нефтегазовое дело», Профиль: Эксплуатация и обслуживание объектов транспорта и хранения нефти, газа и продуктов переработки). СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 1.Гидравлика, гидромашины и гидроприводы: учеб.для втузов / Т. М. Башта, Б. Б. Некрасов, С. С. Руднев. - 2-е изд., перераб. - М. : Машиностроение, 1982. - 423 с. : ил. - Библиогр.: с.418. 2. Гидромеханика: учеб.пособие по решению задач / Л. Н. Раинкина ; РГУ нефти и газа им. И.М. Губкина. - М. : Нефть и газ, 2005. - 131 с. 3.Сборник задач по машиностроительной гидравлике: учеб. пособие для вузов / ред. И. И. Куколевский, ред. Л. Г. Подвидз. - 5-е изд., стереотип. - М. : Изд-во МГТУ им. Н.Э. Баумана, 2002. - 448 с. |
