Гидравлический расчет сложного трубопровода и элементов оборудования. гидравлика. Курсовая работа Гидравлический расчет сложного трубопровода и элементов оборудования
 Скачать 323.76 Kb. Скачать 323.76 Kb.
|
Задача №3.34Исходные данные: Тело в форме цилиндра с полушаровой головкой, размеры которого d = 200 мм, R = 300 мм и масса m = 230 кг, плавает в воде, заполняющей замкнутый сосуд. Установить зависимость между избыточным давлением pи газа в сосуде и погружением h тела под уровнем воды и найти давление, при котором погружение станет равным h=R и полушар начнет выходить из воды. 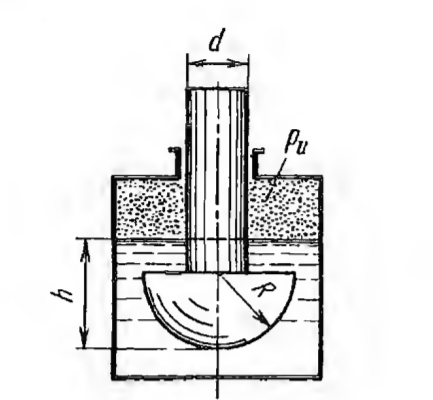 рисунок 3 Решение: 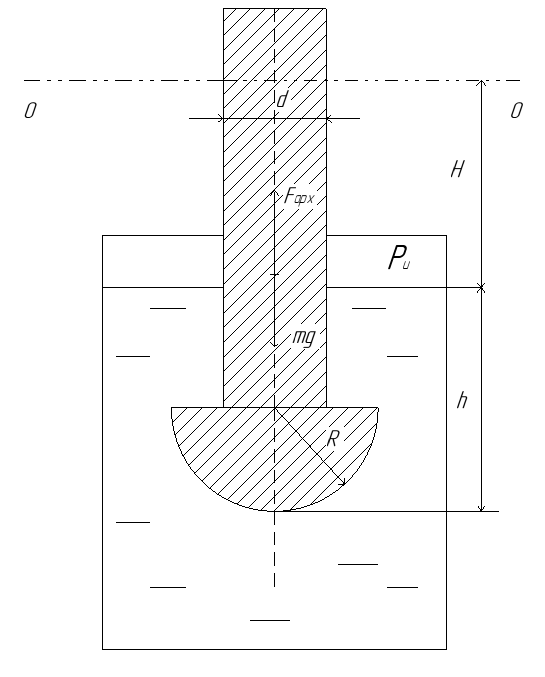 рисунок 4 Расстояние от поверхности до пьезометрической плоскости 0-0 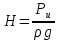 Объем тела давления или объем погруженной части тела 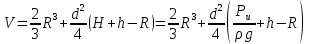 Вертикальная составляющая силы давления 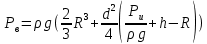 Из условия 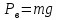 определим: определим: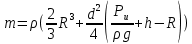 Отсюда выведем зависимость между избыточным давлением Pи газа в сосуде и погружением h тела под уровнем воды 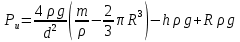 При h=R давление 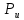 из этой зависимости: из этой зависимости: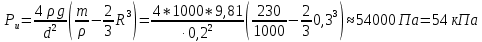 Ответ: 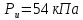 2. Гидростатический расчет сложного трубопровода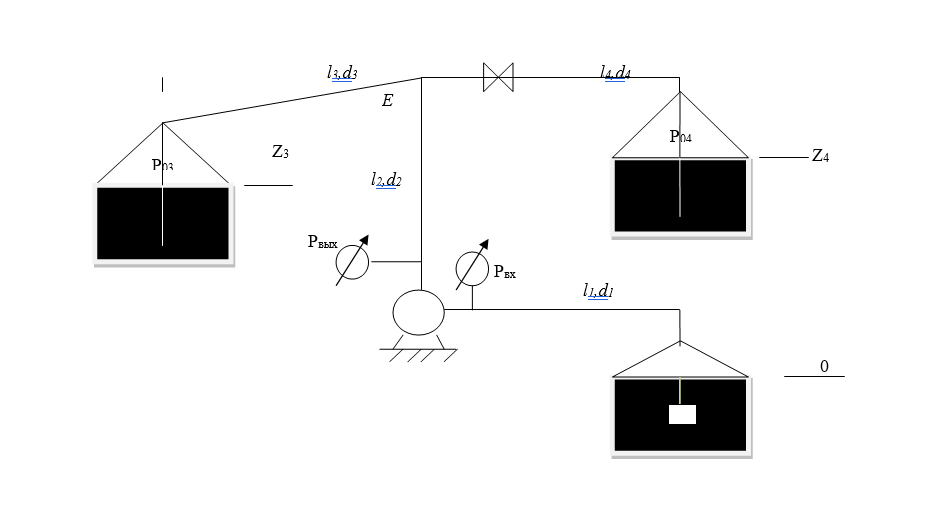 Исходные данные: Проектный расход, м3/часQ-? 0 Перекачиваемая жидкостьρ=900 кг/м3; υ=30*10-6 м2/с Температура перекачки_________________________ Эквивалентная шероховатость труб K= 0,2 мм к
Данную схему трубопровода можно разбить на 4 простых трубопровода, причем трубопровод 1 (l1d1) является всасывающим и рассчитывается отдельно от сложного трубопровода, состоящего из трубы 2 (l2d2), трубы 3 (l3d3) и трубы 4 (l4d4). Составим уравнение Бернулли для трубопровода 1, относительно плоскости отсчета, проведенной через свободную поверхность жидкости в первом резервуаре. При этом начальное сечение соответствует свободной поверхности жидкости в первом резервуаре, а конечное сечение – на входе в насос. Z1 + 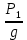 = Zвх + = Zвх + 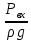 + + 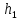 , ,Данное уравнение позволит вычислить Pвх при найденном расходе Q. Составим систему уравнений Бернулли и уравнений расходов для разветвленной части трубопроводной сети. Для трубопровода 2:
Обозначим ZЕ + 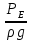 = HE, и преобразуем уравнение к виду: = HE, и преобразуем уравнение к виду:Zвых + 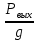 = HE + = HE + 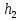 , ,или
Для трубопровода 3:
Для трубопровода 4:
Уравнения расходов:
где Q1, Q2, Q3, Q4 – расходы соответственно 1-го, 2-го, 3-го и 4-го трубопроводов. Q = S, Полученные уравнения сведем в систему:
Для решения полученной системы уравнений рассчитаем гидравлические характеристики каждого трубопровода. 2.1. Гидравлический расчет 2-го трубопровода Расчет трубопровода для = 1 м/с: Q2 = 2S = 1 ⋅ 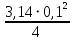 = 0,00785 = 0,00785 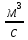 . .По найденным значениям расхода найдем значения числа Рейнольдса в каждом случае: Re = 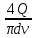 = = 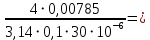 3333,33. 3333,33.Коэффициент Дарси нужно вычислять в зависимости от режима движения жидкости в трубопроводе, который определяем по критическому и граничным числам Рейнольдса: 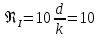 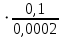 = 5000, = 5000,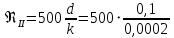 = 250000. = 250000.Анализируя полученные данные, (Reкр < Re < 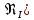 вычисляем коэффициент Дарси по формуле Блазиуса: вычисляем коэффициент Дарси по формуле Блазиуса: = 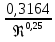 = = 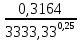 = 0,042. = 0,042.По формуле Дарси – Вейсбаха вычислим значения суммарных потерь напора во втором трубопроводе. Так как во втором трубопроводе нет местных сопротивлений, то при вычислении  h, коэффициент берем равным нулю: h, коэффициент берем равным нулю: h = h = 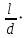 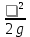 = 0,042 = 0,042 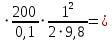 4,24 м. 4,24 м.Найдем величины статического напора 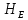 для последующего построения гидравлической характеристики трубопровода: для последующего построения гидравлической характеристики трубопровода: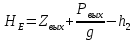 = 2 + = 2 + 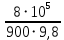 – 4,24 = 88,366 м. – 4,24 = 88,366 м.Результаты расчета сведем в таблицу 1. Таблица 1 – Гидравлический расчет 2-го трубопровода
2.2. Гидравлический расчет 3-го трубопровода: Расчет трубопровода для = 1 м/с: Q2 = 3S = 1 ⋅ 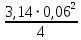 = 0,00283 = 0,00283 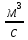 . .По найденным значениям расхода найдем значения числа Рейнольдса: Re = 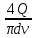 = = 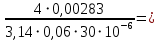 2002,83. 2002,83.Анализируя полученные данные, (Re< Reкр 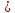 вычисляем коэффициент Дарси по формуле Стокса: вычисляем коэффициент Дарси по формуле Стокса: = 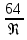 = = 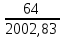 = 0,032 = 0,032По формуле Дарси – Вейсбаха вычислим значения суммарных потерь напора в третьем трубопроводе. Так как в третьем трубопроводе нет местных сопротивлений, то при вычислении  h, коэффициент берем равным нулю: h, коэффициент берем равным нулю: h = h = 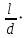 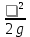 = 0,032 = 0,032 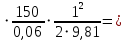 4,08 м. 4,08 м.Найдем величины статического напора 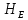 для последующего построения гидравлической характеристики трубопровода: для последующего построения гидравлической характеристики трубопровода: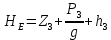 = 6 + = 6 + 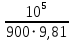 + 4,08 = 21,408 м. + 4,08 = 21,408 м.Таблица 2 – Гидравлический расчет 3-го трубопровода
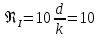 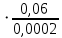 = 3000, = 3000,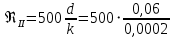 = 150000. = 150000.2.3. Гидравлический расчет 4-го трубопровода: Расчет трубопровода для = 1 м/с: Q2 = 4S = 1 ⋅ 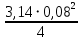 = 0,00502 = 0,00502 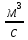 . .По найденным значениям расхода найдем значения числа Рейнольдса: Re = 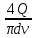 = = 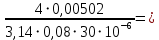 2664,67. 2664,67.Граничные числа Рейнольдса: 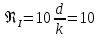 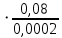 = 4000, = 4000,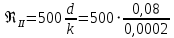 = 200000. = 200000.Анализируя полученные данные, (Reкр 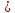 вычисляем коэффициент Дарси по формуле Блазиуса: вычисляем коэффициент Дарси по формуле Блазиуса: = 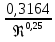 = = 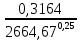 = 0,044. = 0,044.По формуле Дарси – Вейсбаха вычислим значения суммарных потерь напора в четвертом трубопроводе. Так как в четвёртом трубопроводе есть местные сопротивления, то при вычислении  h, коэффициент берем равным 0,15: h, коэффициент берем равным 0,15: h = ( h = (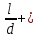 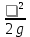 = (0,044 = (0,044 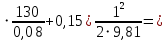 3,65 м. 3,65 м.Найдем величины статического напора 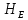 для последующего построения гидравлической характеристики трубопровода: для последующего построения гидравлической характеристики трубопровода: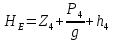 = 6 + = 6 + 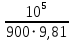 + 3,65 = 20,973 м. + 3,65 = 20,973 м.Таблица 3 – Гидравлический расчет 4-го трубопровода
На основании вычисленных данных строим график уравнений (2), (3), (4), (5) в координатах H – Q.  A 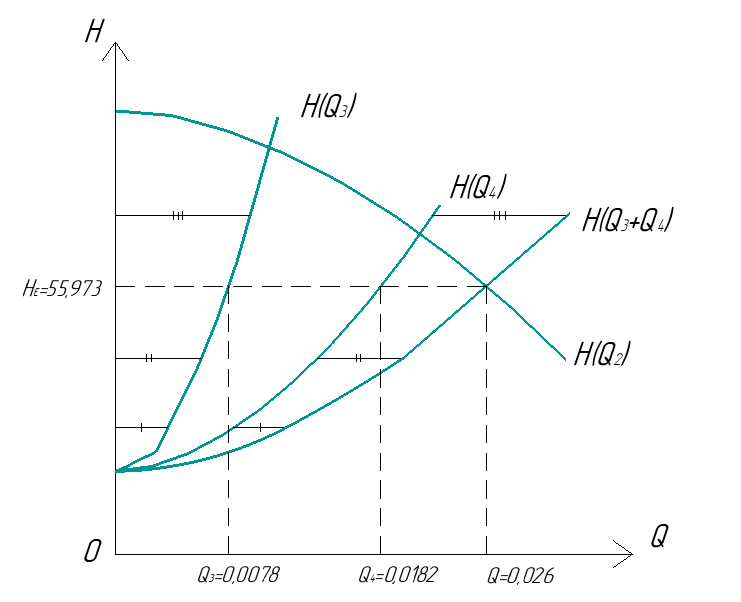 График 1 Построенные кривые на графике 1 являются графическим изображением уравнений (2), (3), (4). На основании уравнения (5), сложив графически кривые H(Q3) и H(Q4) путем добавления расхода в трубопроводе 3 к расходу в трубопроводе 4 при одинаковом значении напора, получаем кривую, представляющую собой эквивалентную гидравлическую характеристику трубопроводов 3 и 4, т.е. H(Q3 + Q4). Точка А пересечения кривых H(Q2) и H(Q3 + Q4) дает графическое решение относительно напора в узле E и расхода Q. Так как кривая H(Q3 + Q4) получена путем сложения расходов в трубопроводах 3 и 4, то, проведя горизонтальную прямую от точки А до пересечения с кривыми H(Q3) и H(Q4), получим значения расходов Q3 и Q4. Q = Q2 = 0,026 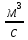 = 93,6 = 93,6 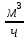 , ,Q3 = 0,0078 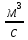 = 28,08 = 28,08 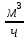 , ,Q4 = 0,0182 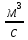 = 65,52 = 65,52 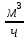 . .Приведенные расчеты показали, что проектный расход в трубопроводе составляет Q = 93,6 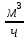 . .Для нахождения Pвх составим уравнение Бернулли для участка трубопровода l1d1: Z1 + 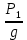 = Zвх + = Zвх + 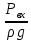 + + 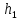 . .Расход на участке l1d1 трубопровода равен расходу на участке l2d2. Отсюда можем найти скорость потока 1: 1 = 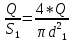 , ,где S1 – площадь сечения трубопровода 1. Подставляя численные значения получим: 1 = 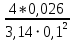 = 3,312 = 3,312 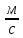 . .Определим число Рейнольдса: Re = 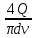 = = 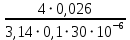 = 11040. = 11040.Вычислим граничные значения ReI и ReII: 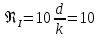 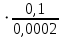 = 5000, = 5000,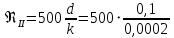 = 250000. = 250000.Сравнивая вычисленное число Re с граничными и критическим ReI < Re < ReII делаем вывод, что режим движения турбулентный, зона гидравлических гладких труб, и определяем по формуле Альтшуля: = 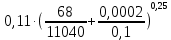 =0,033 =0,033Находим суммарные потери напора на участке l1d1, с учетом местного сопротивления в виде плавного колена (90), коэффициент которого 1 = 0,23, и прижимной коробки трубы с клапаном и сеткой, с коэффициентом 2 = 7 [2]: h1 = (1 + 2 + 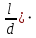 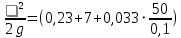 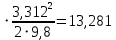 м. м.Выразим Pвх из уравнения Бернулли для первого трубопровода: Pвх = g(Z1 – Zвх + 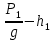 ), ),Подставляя численные значения получим: Pвх = 900 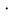 9,8 (0 – 2 9,8 (0 – 2 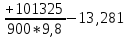 ) = – 33453,42 Па. ) = – 33453,42 Па. |

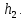
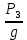 +
+ 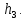
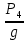 +
+ 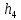 .
.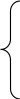 HE = Zвых +
HE = Zвых + 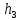
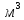 /с
/с