геометрическое выражение произв. Курсовая работа Гиперболические функции и их производные
 Скачать 137.6 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Чувашский государственный педагогический университет им. И.Я. Яковлева» Физико-математический факультет Кафедра математики и физики КУРСОВАЯ РАБОТА «Гиперболические функции и их производные» Руководитель
Чебоксары 2022 Введение Содержание Гиперболические функции 1.1. Связь с тригонометрическими функциями Производные гиперболических функций Обратные гиперболические функции Введение Гиперболические функции часто встречаются при вычислении различных интегралов. Некоторые интегралы от рациональных функций и от функций, содержащих радикалы, довольно просто выполняются с помощью замен переменных с использованием гиперболических функций. Аналогично тому, как матрицы вида 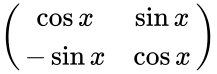 описывают повороты двумерного евклидова пространства, матрицы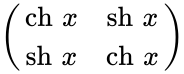 описывают повороты в простейшем двумерном пространстве Минковского. В связи с этим гиперболические функции часто встречаются в теории относительности. Однородная веревка или цепочка, свободно подвешенная за свои концы, приобретает форму графика функции  (в связи с чем график гиперболического косинуса иногда называют цепной линией). Это обстоятельство используется при проектировании арок, поскольку форма арки в виде перевёрнутой цепной линии наиболее удачно распределяет нагрузку.Гиперболические функции Гиперболические функции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. В математике, механике, электротехнике и некоторых других дисциплинах встречаются гиперболические функции, определяемые следующими формулами: Гиперболические функции задаются следующими формулами: гиперболический синус: 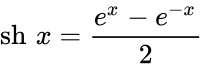 (в зарубежной литературе обозначается  )Существует сленговые названия: «шинус», «шимус»(?). Однако их использование не научно. гиперболический косинус: 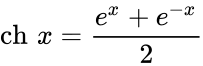 (в зарубежной литературе обозначается  )Существует сленговые названия: «чосинус», «кошинус». Однако их использование не научно. гиперболический тангенс: 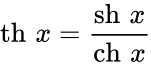 (в зарубежной литературе обозначается  ).Существует сленговые названия: «щангенс», «тахинус». Однако их использование не научно. Иногда также определяются гиперболический котангенс: 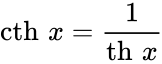 ,Существует сленговые названия: «кочангенс», «кохинус». Однако их использование не научно. гиперболические секанс и косеканс: 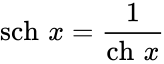 , 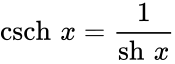.Геометрическое определение Ввиду соотношения 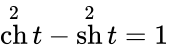 гиперболические функции дают параметрическое представление гиперболы  ( ,  ). При этом аргумент  , где S — площадь криволинейного треугольника OQR , взятая со знаком «+», если сектор лежит выше оси OX , и «−» в противоположном случае. Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом. Связь с тригонометрическими функциями Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента.  .Важные тождества 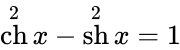  Чётность:    Формулы сложения:   Формулы двойного угла: 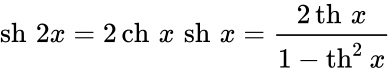 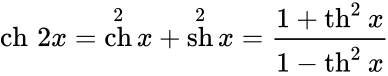 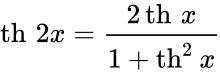 Производные: 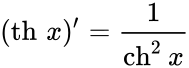 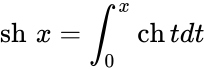 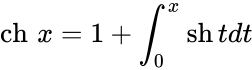 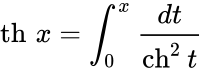   Интегралы: 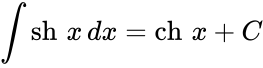 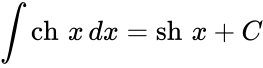 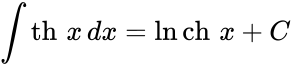 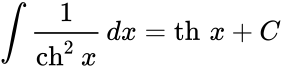 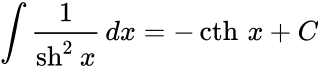 Заключение Таким образом, мы рассмотрели …. Список использованных источников |