Метод наименьших квадратов. Курсовая. МНК. Курсовая работа На учебную практику (20202021 учебный год)

Название	Курсовая работа На учебную практику (20202021 учебный год)
Анкор	Метод наименьших квадратов. Курсовая
Дата	16.12.2020
Размер	359.46 Kb.
Формат файла
Имя файла	МНК.docx
Тип	Курсовая #161163

Министерство науки и высшего образования Российской Федерации

федеральное государственное автономное образовательное учреждение высшего образования

“Казанский (Приволжский) федеральный университет”

Курсовая работа

На учебную практику

(2020/2021 учебный год)

Институт/факультет/подразделение Инженерный институт/Техническая физика

Направление подготовки (специальность) Техническая физика

Место прохождения практики КФУ Институт физики, ул. Кремлевская, д.16а

(наименование организации, адрес организации)

Обучающийся Газизова Гузель Илиясовна, 1 курс, группа 16-003

(ФИО, курс, группа)

Срок прохождения практики с “2” сентярбя 2020 г. По “29” декабря 2020 г.

Руководитель практики от Университета____________________________________

(ФИО, должность, учебное заведение)

Содержание работы:

№ п/п	Индивидуальные задания (перечень и описание работы)	Сроки выполнения
1.	Аппроксимация функции. Методом наименьших квадратов аппроксимирована зашумленная экспоненциальная функция.	С 03.11.2020 по 29.12.2020

Руководитель практики от Университета _________/__________________/

(подпись) (ФИО)

С настоящей курсовой работой, с программой практики по соответствущему практике направлению подготовки (специальности) ОЗНАКОМЛЕН(А)

_________/__________________/

(подпись) (ФИО обучающего)

СОДЕРЖАНИЕ

1.Содержание…………………………………………………………………………………… 2

2.Введение……………………………………………………………….……………………… 3

3.Линейная регрессия………………………………………………………………………..… 5

4.Код программы………………………………………………………………………..……... 7

5.Результат работы программы……………………………...…….………………………… 11

6.Вывод………………………………………………………………………………………... 12

7.Список используемой литературы……………………………………………………….... 13

ВВЕДЕНИЕ

Задача. Аппроксимация функции методом наименьших квадратов.

Одной из самых распространенных задач экспериментальной физики является задача статистической обработки данных эксперимента, в частности, составление эмпирических формул для нахождения зависимости одной величины от другой, когда известна таблица их значений, полученных в результате некоторой серии физических экспериментов. Для получения параметров таких формул обычно используется метод наименьших квадратов.

Предположим, что предметом наблюдений (измерений) в исследуемой системе служит величина у, значения которой меняются в зависимости от некоторого аргумента х. Общей задачей здесь является нахождение функции определенного вида, которая наилучшим образом отражает зависимость между величинами xи y. Подбор математической формулы, наилучшим образом описывающей экспериментальные данные, выполняется с помощью регрессионного анализа. Математическая постановка задачи заключается в следующем. Зависимость величины y от переменнойx зарегистрирована множеством точек (x_i,y_i), при этом в каждой точке значения y_i отображают действительные значения y(х_i) со случайной погрешностью s_i, распределенной, как правило, по нормальному закону. По совокупности значений y_iтребуется подобрать функцию f(x_i, a₀, a₁, … , a_k), отображающую зависимость y(x), т.е.

y_i = f(x_i, a₀, a₁, … , a_k)+ s_i_,

при этом погрешность s_iдолжна быть минимизирована.

Аппроксимирующая функция f может быть математической функцией любого типа, линейной комбинацией различных функций или функциональным рядом из степенных, тригонометрических и любых других функций. В основу ее построения желательно закладывать априорные (теоретические) предположения о сущности изучаемого явления.

Обычно ограничиваются функциями одного из следующих видов:

линейная: y=ax+b или y=a₁x₁+a₂x₂+b

(зависимость от двух параметров)

квадратичная: y=ax²+bx+c,

(иногда - полином более высокой степени)

степенная: y=axⁿ
экспоненциальная: y=ae^bx
логарифмическая: y=a∙ln(x)+b
гиперболическая: y=1/(ax+b) или y=a/x+b

При полном отсутствии априорной информации о распределении случайной составляющей данных на начальном этапе обычно используется квадратичная мера приближения (дисперсия).

Погрешность приближения вычисляется методом наименьших квадратов (МНК). Для этого выполняется минимизация функции квадратов остаточных ошибок

.

Для определения параметров a₀, a₁, … , a_kфункция остаточных ошибок дифференцируется по всем параметрам; полученные уравнения частных производных приравниваются нулю и решаются в совокупности относительно всех значений параметров. Виды регрессии обычно называются по типу аппроксимирующей функцииf: полиномиальная, экспоненциальная, логарифмическая и т.п.

Требование минимального разброса будет удовлетворено, если минимизировать s(a₀, a₁, … , a_k). Как известно, необходимым условием того, что функция приобретает минимальное значение, является то, что ее первая производная (или частные производные для функции многих переменных) равна нулю.

Применение метода наименьших квадратов имеет смысл, если число экспериментальных точек n больше числа определяемых коэффициентов k.

Линейная регрессия

Рассмотрим реализацию МНК применительно к уравнению вида:

y = ax + b.

Графическая иллюстрация линейной аппроксимации набора данных представлена на рис. 1.1.

Рис. 1.1. Аппроксимация экспериментальных данных (точек)
линейной зависимостью

Для нахождения коэффициентов а, b искомой прямой необходимо минимизировать сумму квадратов расстояний y_i по ординате от всех точек (х_i,y_i) до прямой. Цель – определить коэффициенты a и b таким образом, чтобы величина приняла наименьшее значение.

Известно, что для поиска экстремумов гладких функций нескольких переменных нужно находить критические точки, т. е. те точки, в которых все частные производные функции равны нулю. В нашем случае необходимо решить следующую систему:

Это система двух линейных уравнений с двумя неизвестнымиaи b. Перепишем ее в следующем виде:

Получим систему нормальных уравнений метода наименьших квадратов.

Введем стандартные в статистике обозначения для статистических моментов М выборки:

(*)

Тогда наша система перепишется в следующем виде:

и может быть решена, например, методом Крамера, а именно:

.

Код программы:

#include "graphics.h"

#include

#include

#include

#include

double X1, X2, Y1,Y2,a,b1,b,m,DIs;

float fun_start(float X){

return 2*exp(0.1*X); ; //Исходная функция

}

double px(double X)

{

return (X-X1)/(X2-X1)*getmaxx();(); //Переход от математических координат к экранным

}

double f(double X)

{

return b1*exp(a*X); ;//Функция для который мы будем искать a,b

}

double py(double Y)

{

return getmaxy()-(Y-Y1)/(Y2-Y1)*getmaxy();

}

int main()

{

int i,n;

int j=0;

printf("Vvedite kol-vo tochek:");

scanf("%d", &n);

float buffer,x[n],y[n],c[n],t[n];

srand(time(NULL));

for (i=0;i
{

x[i]=(float)((rand()%10000))/1000 - 5; ;//Заполнение массива, элементами которого являются значения аргумента, рандомными числами

}

}

}}

for (j=0;j
{

c[j]=(float)((rand()%1000))/1000-0.5; ;//задание шума

y[j]=(2*exp(0.1*x[j]))+c[j];

t[j]=log(y[j]);

printf("x[%d] =%3.3f\t", j, x[j]);

printf("c[%d] = %5.3f\t", j, c[j]);

printf("y[%d] = %5.3f\t", j, y[j]);

printf("t[%d] = %5.3f\n", j, t[j]);

}

double Mx = 0;

double My = 0;

double Mxx = 0;

double Mxy = 0;

double Dis = 0;

for(j=0;j
{

Mx += x[j]/n;

My += t[j]/n;

Mxx += (x[j]*x[j])/n;

Mxy += (x[j]*t[j])/n;

}

a=(Mxy-My*Mx)/(Mxx-Mx*Mx);

b=(Mxx*My-Mx*Mxy)/(Mxx-Mx*Mx); //Решение системы методом Крамера

b1=exp(b);

for(j=0;j
DIs += pow((f(x[j])-y[j]),2); //подсчетДисперсии

printf("a=%.3f b1=%2.3f DIs=%.3f\n",a,b1,DIs);

printf("Y=%.3f*exp(%2.3f*x)",b1,a);

initwindow(900, 600);

double X, Y;

int nPoints;

double dx;

X1=-5;

X2=5; //Верхняя и нижняя границы аргумента

nPoints=getmaxx();

dx=(X2-X1)/nPoints;

Y1=-2;

Y2=4; // Верхняя и нижняя границы функции

setcolor(BLUE);

moveto(px(x[0]), py(y[0]));

for (i=0;i
{

circle(px(x[i]), py(y[i]),2);

setfillstyle(SOLID_FILL, BLUE);

floodfill(px(x[i]), py(y[i]),BLUE); //Выводточекнаэкран

}

setcolor(YELLOW);

setcolor(GREEN);

Y=f(x[0]);

moveto(px(x[0]), py(Y));

for (X=X1; X<=X2; X+=dx)

{

Y=f(X);

lineto(px(X), py(Y)); //Рисование искомой функции

}

setcolor(WHITE);

outtextxy (px(0)+5, py(0)+5, "0");

outtextxy (px(1), py(0)+5, "1");

outtextxy (px(-1)-15, py(0)+5, "-1");

outtextxy (px(0)-40, py(1)-10, "1");")//Обозначение Оси Х и Y

outtextxy (px(0)-40, py(2)-10, "2");

outtextxy (px(X2)-13, py(0)+10, "X");

outtextxy (px(0)-20, py(Y2)+5, "Y");

line(px(0), py(Y2), px(0)+4, py(Y2)+20); //стрелки

line(px(0), py(Y2), px(0)-4, py(Y2)+20);

line(px(X2), py(0), px(X2)-20, py(0)+4);

line(px(X2), py(0), px(X2)-20, py(0)-4);

for(X=-12;X<=X2;X+=1)

line(px(X), py(0)+5, px(X), py(0)-5);

for(Y=-1;Y<=Y2;Y+=1)

line(px(0)+5, py(Y), px(0)-5, py(Y)); )//Рисованиештрихов

line(px(X1), py(0), px(X2), py(0)); //os X

line(px(0), py(Y1), px(0), py(Y2));//os Y

setcolor(LIGHTMAGENTA );

for (X=-12; X<=X2; X+=dx)

{

Y=fun_start(X);

putpixel(px(X), py(Y),15);

}

getch();

closegraph();

return 0;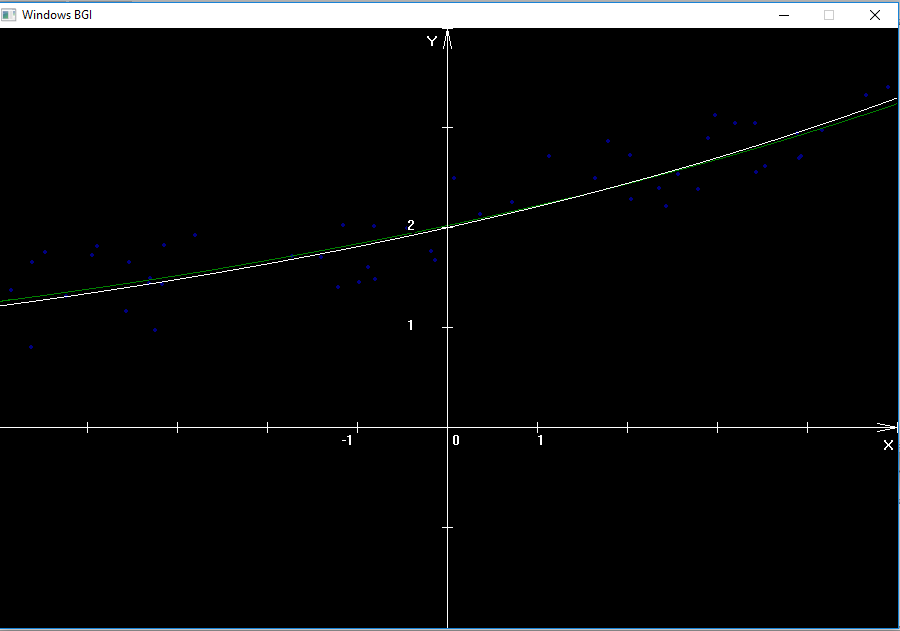

}

В результате работы программы мы получаем- график, коэффиценты и уравнение: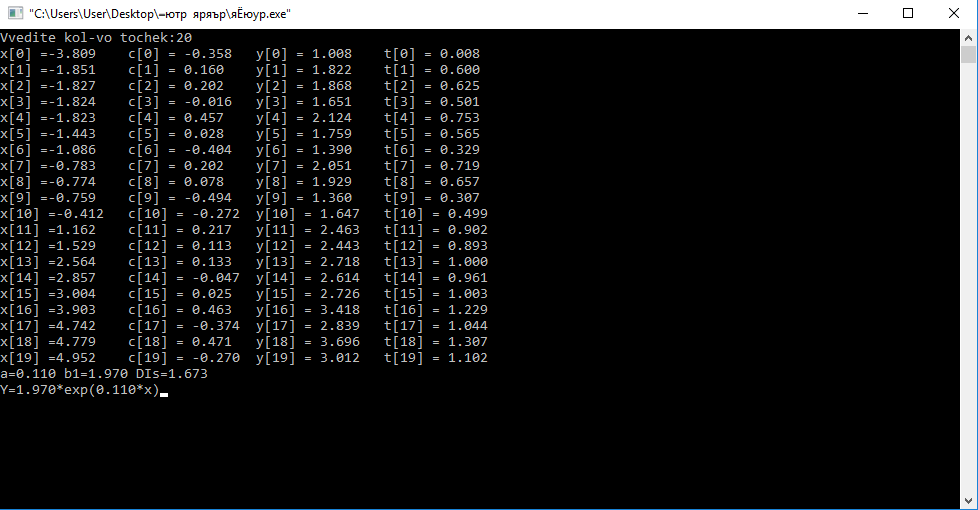

Где Dis-это среднее квадратичное отклонение, Аппроксимирующая функция : y=1.970*exp(0.110*x), (С-шум «эксперимента)

ВЫВОД

Мы произвели аппроксимацию функции методом наименьших квадратов, а именно зашумленная экспоненциальная функция. В результате работы программы мы получили график, коэффиценты и уравнение. Можно сделать вывод, что программа успешно произвела все вычисления и вывела наглядный график.

Список используемой литературы:
1)Г.М. Тептин, О.Г. Хуторова, Ю.М. Стенин, А.А. Журавлев, В.Р. Ильдиряков, В.Е. Хуторов, К.В. Скобельцын «Численные методы в физике и радиофизике» .Методическое пособие. -Казань. -2013, 38 с.

2)Хуторова О. Г., Стенин Ю. М., Фахртдинов Р. Х., Зыков Е. Ю., Журавлев А. А. Практикум по информатике. Программирование на языке Си. Учебнометодическое пособие. Казань: Казанский государственный ун-т, 2009. – 46 c.

3) Программирование на языке Си / А.В.Кузин, Е.В.Чумакова - М.: Форум, НИЦ ИНФРА-М, 2015. - 144 с.

4) Царев, Р. Ю. Программирование на языке Си [Электронный ресурс] : учеб. пособие / Р. Ю. Царев. – Красноярск : Сиб. федер. ун-т, 2014. – 108 с. - Режим доступа: http://znanium.com/catalog/product/510946