Написать программу, позволяющую выполнять арифметические действия над двоичными, восьмеричными или шестнадцатеричными числами. Курсовая программирование. Курсовая работа Название дисциплины Программирование Тема
 Скачать 313.88 Kb.
|
Основные данные о работе
СодержаниеОсновные данные о работе 1 Содержание 2 Введение 3 Основная часть 5 1 Системы счисления 5 1.1 Десятичная система счисления 5 1.2 Двоичная система счисления 5 1.3 Восьмеричная система счисления 6 1.4 Шестнадцатиричная система счисления 7 2 Разработка алгоритмов 8 3 Разработка пользовательского интерфейса 12 Заключение 17 Глоссарий 18 Список использованных источников 19 Приложения 20 ВведениеСистемой счисления называется совокупность приемов наименования и записи чисел. В любой системе счисления для представления чисел выбираются некоторые символы (их называют цифрами), а остальные числа получаются в результате каких-либо операций над цифрами данной системы счисления. Система называется позиционной, если значение каждой цифры (ее вес) изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Число единиц какого-либо разряда, объединяемых в единицу более старшего разряда, называют основанием позиционной системы счисления. Если количество таких цифр равно 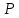 , то система счисления называется -ичной. Основание системы счисления совпадает с количеством цифр, используемых для записи чисел в этой системе счисления.Запись произвольного числа 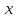 в -ичной позиционной системе счисления основывается на представлении этого числа в виде многочлена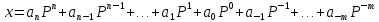 Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами. При этом нужно только пользоваться теми таблицами сложения и умножения, которые соответствуют данному основанию 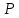системы счисления.Тема курсовой работы – «Арифметические операции над числами различных систем счисления». Цель курсовой работы – разработка программного обеспечения, осуществляющего арифметические действия над числами выбранной системы счисления. Для достижения цели необходимо решить следующие задачи: Рассмотреть системы счисления; Разработать алгоритмы арифметических действий; Разработать интерфейс пользователя. Основная часть1 Системы счисления1.1 Десятичная система счисленияДесятичная система счисления пришла из Индии (не позднее VI века нашей эры). Алфавит этой системы: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} — всего 10 цифр, таким образом, основание системы счисления – 10. Число записывается как комбинация единиц, десятков, сотен, тысяч и так далее. Пример: 1998=8*100 + 9*101 + 9*102 + 1*103. В этой системе 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, но информацию несет не только цифра, но и место, на котором цифра стоит (то есть ее позиция). Самая правая цифра числа показывает число единиц, вторая справа – число десятков, следующая – число сотен и т.д. 1.2 Двоичная система счисленияДвоичная система счисления была придумана математиками и философами ещё до появления компьютеров (XVII — XIX вв.). Выдающийся математик Лейбниц говорил: "Вычисление с помощью двоек... является для науки основным и порождает новые открытия... При сведении чисел к простейшим началам, каковы 0 и 1, везде появляется чудесный порядок". Позже двоичная система была забыта, и только в 1936 — 1938 годах американский инженер и математик Клод Шеннон нашёл замечательные применения двоичной системы при конструировании электронных схем. В двоичной системе числа записываются с помощью двух цифр: 0,1. Перевод десятичного числа в двоичное число: 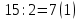 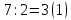 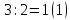 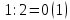 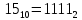 Существуют системы счисления, родственные двоичной. При работе с компьютерами иногда приходится иметь дело с двоичными числами, так как двоичные числа заложены в конструкцию компьютера. Двоичная система удобна для компьютера, но неудобна для человека — слишком длинные числа неудобно записывать и запоминать. На помощь приходят системы счисления, родственные двоичной — восьмеричная и шестнадцатеричная. 1.3 Восьмеричная система счисленияВ восьмеричной системе числа записываются с помощью восьми цифр: 0,1,2,3,4,5,6,7, а сама восьмерка числом 10. Удобство восьмеричной системы счисления заключается в том, что переход от восьмеричной к двоичной очень прост: достаточно каждую восьмеричную цифру заменить ее двоичным представлением (двоичной триадой), в соответствии с приведенной ниже таблицей.
Например, 5028 = 101 000 0102 Достаточно прост и обратный переход от двоичной с/с к восьмеричной. Для этого в двоичной записи числа нужно выделить триады (влево и вправо от десятичной точки) и заменить каждую триаду соответствующей восьмеричной цифрой. В случае необходимости неполные триады дополняются нулями. Например, 1 111 1102 = 001 111 1102 = 1768 1.4 Шестнадцатиричная система счисленияШестнадцатеричная система счисления, так же как восьмеричная, широко используется в компьютерной науке из-за простоты перевода в нее двоичных чисел. В случае шестнадцатеричной записи числа получаются более компактными. В качестве алфавита шестнадцатеричной системы счисления используются цифры от 0 до 9 и шесть первых латинских букв – A, B, C, D, E, F. При переводе в десятичную систему буквы заменяются числами 10, 11, 12, 13, 14, 15 соответственно. При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не кратно четырем, первая четверка дописывается нулями впереди. Каждой четверке соответствует одноразрядное число шестнадцатеричной системы счисления.
0100 1100 0101 = 4 C 5 2 Разработка алгоритмовДля выполнения арифметических действий над числами будет использоваться следующий алгоритм: 1. Проверка введенных чисел на принадлежность к выбранной системе счисления; 2. Перевод введенных чисел в десятичную систему; 3. Выполнение арифметических действий над десятичными числами (+, -, *, /); 4. Перевод результата в выбранную систему счисления и вывод на экран. Функция определения принадлежности введенного числа выбранной системе счисления: function CheckInput(ch:String;r:Byte):Boolean; var i,j:Byte; res:Boolean; begin CheckInput:=True; For i:=1 to Length(ch) do begin res:=False; For j:=1 to r do if ch[i]= digit[j] then begin res:=True; break; end; if (res=False) and (ch[i]<>',') then begin CheckInput:=False; break; end; end; end; Где ch – строковое значение введенного числа, r – основание системы счисления. Функция перевода из любой системы счисления в десятичную систему целого числа: function ToDec(var ss: string; cc: byte): integer; var i, n, sum: integer; begin sum := 0; n := length(ss); for i := 1 to n do begin dec(n); sum := sum + round((pos(ss[i], digit) - 1) * exp(ln(cc) * n)); end; ToDec := sum; end; Где ss – строковое значение введенного числа, cc – основание системы счисления. Функция перевода из десятичной системы счисления в любую систему счисления целого числа: function Cel(d: real; c: integer): string; var s: string; n2: integer; begin n2 := round(int(d)); s := ''; repeat s := ((digit[n2 mod c + 1]) + s); n2 := n2 div c; until (n2 = 0); Cel := s; end; Где d – строковое значение введенного числа, c – основание системы счисления. Процедура разделения дробного числа на целое и остаток: procedure Del(var ss: string); var i: integer; begin ind := 0; s2 := ''; for i := 1 to length(ss) do if ss[i] in [',', '.'] then begin ind := i; break end else s2 := s2 + ss[i]; s3 := ''; if ind <> 0 then begin delete(s, 1, ind); s3 := ss; end; end; Функция перевода дробной части из десятичной системы счислению в любую систему: function Drob(var d: real; t, c: integer): string; var s: string; l2, k: real; i: integer; begin k := d - int(d); s := ''; i := 0; if t <> 0 then begin repeat l2 := k * c; k := frac(l2); s := s + digit[round(int(l2)) + 1]; inc(i); until i = t; end else s := '0'; Drob := s; end; Функция перевода дробной части из любой системы счислению в десятичную систему: function drob2(ss: string; c: integer): real; var i: integer; sum: real; begin sum:=0; for i := 1 to length(ss) do sum := sum + (pos(ss[i], digit) - 1) * exp(ln(c) * -i); drob2 := sum; end; 3 Разработка пользовательского интерфейсаДля удобства работы пользователя с программой разработаем пользовательский интерфейс. На форме слева расположим блок для выбора системы счисления. Далее поля для ввода чисел и поле для вывода результата. Под полями ввода разместим кнопки с обозначениями арифметических действий. При нажатии на них будет формироваться и выводится результат. В правом нижнем углу разместим кнопку «Выход» для завершения работы с программой. Интерфейс пользователя представлен на рисунке 1. 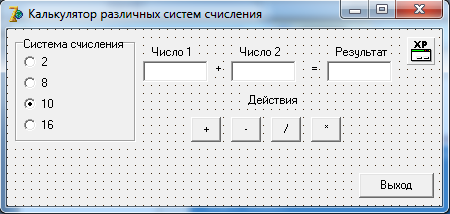 Рисунок 1. Интерфейс пользователя Проведем тестирование разработанного программного обеспечения. 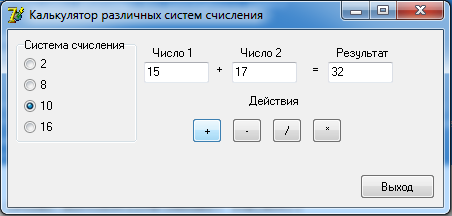 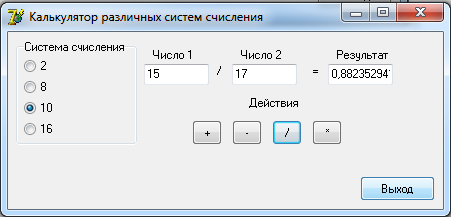 Рисунок 2. Операции над десятичными числами При вводе неверного числа программа выдает об этом ошибку, очищает поле и переводит в него фокус для повторного ввода. 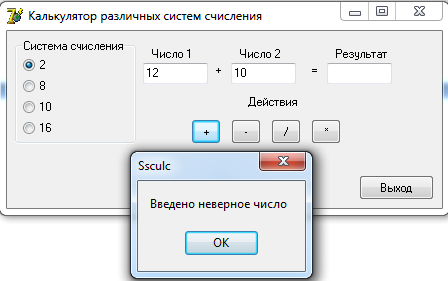 Рисунок 3. Ошибка ввода 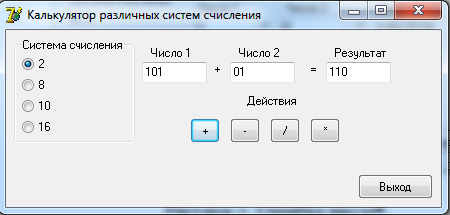 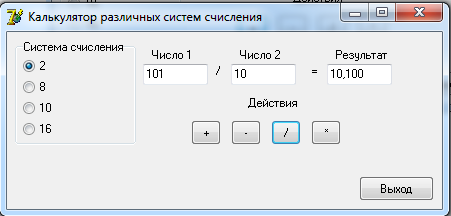 Рисунок 4. Операции над двоичными числами 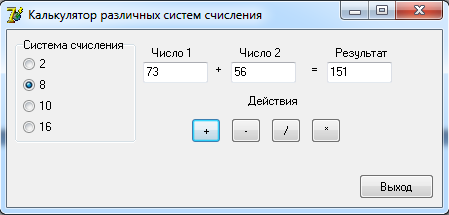 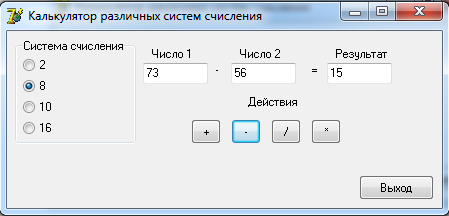 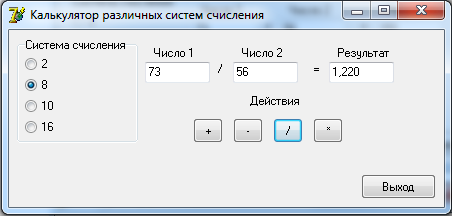 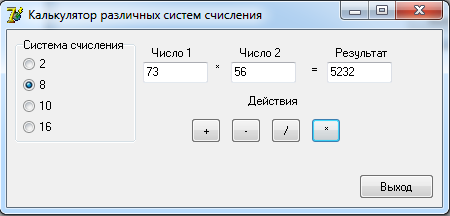 Рисунок 5. Операции над восьмеричными числами 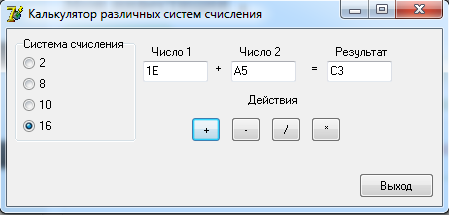 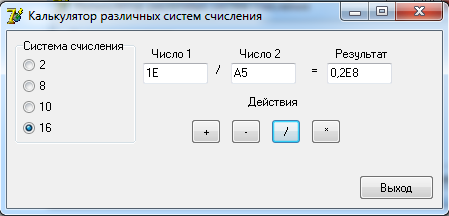 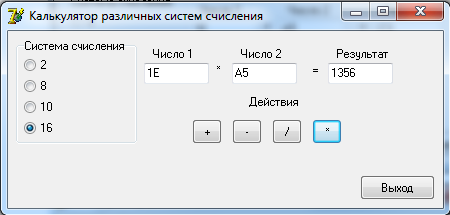 Рисунок 6. Операции над шестнадцатиричными числами Проверка показала, что разработанное программное обеспечение работает корректно. ЗаключениеВ ходе выполнения курсовой работы были рассмотрены популярные системы счисления и способы перевода чисел из одной системы счисления в другую. Далее были разработаны процедуры и функции для перевода чисел одной системы счисления в другую, разделения числа на целую и дробную части, проверку числа на принадлежность к системе счисления. Результатом стало ПО «SSCulc», которое производит арифметические действия над числами различных систем счисления. Программа была проверена на верность вычислений и может быть использована как калькулятор. Глоссарий
Список использованных источников
Приложения
|