Курсовая работа оценка безопасности систем человек машина среда

• Название: Курсовая работа оценка безопасности систем человек машина среда
• Дата: 27.04.2023
• Размер: 0.72 Mb.
• Имя файла: 41409-KURSOVAYa_Proizodstvennaya_bezopasnost_isakovoy.doc
• Тип: Курсовая; #1094382
• страница: 2 из 3

5. МОДЕЛИРОВАНИЕ ВНЕЗАПНЫХ ОТКАЗОВ

Построим интегральную функцию экспоненциального распределения:

где  — интенсивность отказов.
Интенсивность отказов рассчитывается по формуле:



где Т_ср — среднее время наработки на отказ.

Примем среднюю наработку на отказ устройства при срезе валика (Х₃ ) Тср = 20000 час;

F(5000)=0,3 F(50000)=0,92

F( 10000)=0,4 F(60000)=0,95

F(20000)=0,6 F(70000)=0,97

F(30000)=0,8 F(80000)=0,98

F(40000)=0,9 F(90000)=0,99


По расчетным данным построим интегральную функцию экспоненциального распределения. На оси абсцисс отложим время tв 34 раза больше Т_ср. На оси ординат — значение функции F(t).

На основе метода «Монте-Карло» промоделируем вероятность случайных отказов. Выбрасываем с помощью генератора случайных чисел числовую последовательность R в диапазоне значений (01).

Интегральная функция экспоненциального распределения,
=1,2510^-5, 1/час.

Временная выборка из пяти реализаций для шести элементов (X₃) t10³ час

m n		Количество элементов						t0	tобщ	t0/tобщ
		1	2	3	4	5	6
Количество реализаций	1
	2
	3
	4
	5
Итого:

Далее временные значения t_i, приведенные в таблице, сравниваем с Т_ср/2, поскольку нас интересует поведение системы в первый полупериод эксплуатации. Затем получим время t₀ нерабочего состояния элемента системы Х₉, выбирая лишь те случаи, когда t_i<Т_ср/2. Расчет производится по формуле



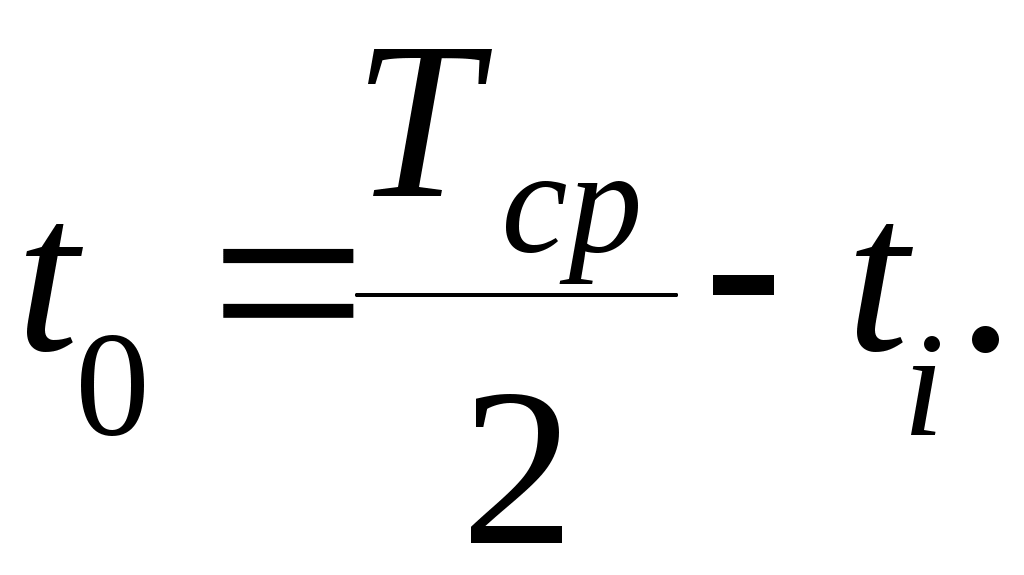
Полученное значение t₀ заносим в таблицу, указав его в скобках, затем суммируем нерабочее время в единичной реализации t₀ и берем отношение к сумме общего времени t_общ работы элемента в этой реализации. На основе полученных значений определим вероятность отказа элемента системы Х₉ для данной реализации по формуле:



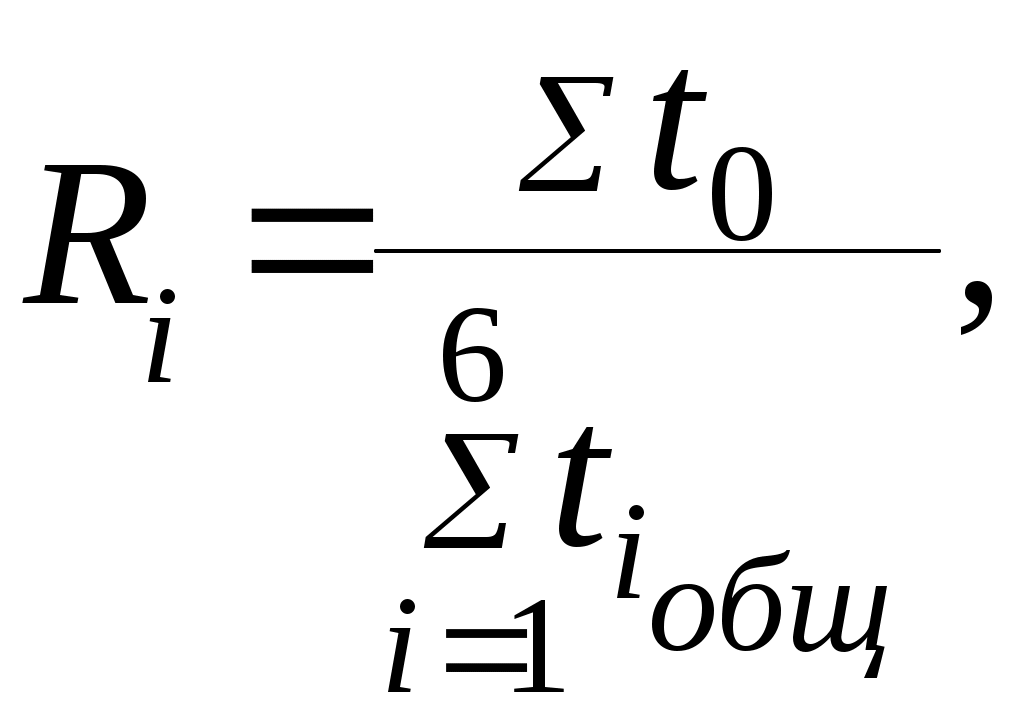
и так для каждой реализации.

Вероятность отказа элемента системы Х₃ является средним арифметическим этих значений:
R_X=1/5ΣR_i,
R_X9=
Аналогично определяем вероятности отказов элементов системы R_X4, R_x4, R_x10.
Примем среднюю наработку на отказ устройства при поломке корпуса (X₄) Т_ср = 80 000 час;

F(5000)=0,2 F(80000)=0,93

F(10000)=0,3 F(100000)=0,96

F(20000)=0,5 F( 120000)=0,98

F(40000)=0,7 F( 140000)=0,99
F(60000)=0,9




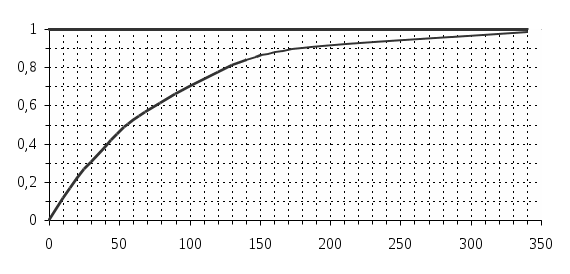
Интегральная функция экспоненциального распределения,
=1,2510^-5, 1/час.

Временная выборка из пяти реализаций для шести элементов (X₄) t10³ час

m n		Количество элементов						t0	tобщ	t0/tобщ
		1	2	3	4	5	6
Количество реализаций	1
	2
	3
	4
	5
Итого:

R_X4=

Примем среднюю наработку на отказ устройства при поломке крышке (Х₇) Т_ср=80000 час.
График

Временная выборка из пяти реализаций для шести элементов (Х₇) t10³ час
Таблица
R_X7=