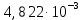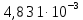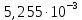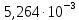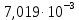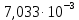Курсовая работа Электротехника ВГТУ 16 вариант. Курсовая работа по дисциплине Электротехника и электроника
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФГБОУ ВО «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Факультет радиотехники и электроники Кафедра конструирования и производства радиоаппаратуры КУРСОВАЯ РАБОТА по дисциплине «Электротехника и электроника» Расчет линейной электрической цепи при гармоническом воздействии Вариант № 16
Воронеж 2021 Задание к курсовой работе 1. Каждому студенту в соответствии с порядковым номером по журналу выбрать вариант схемы по рисунку 1. Различные конфигурации схемы образуются в зависимости от положения ключей «К1 - К5», которые устанавливаются по номеру варианта, представленному в двоичном коде. Номера позиций единиц и нулей в номере варианта следуют слева направо. 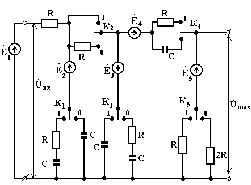 Рисунок 1 – Схема электрической цепи для выбора варианта 2. Определить величины элементов схемы рисунка 1 и частоту генераторов с помощью следующих формул:
где N - номер студента по журналу, n - номер элемента в схеме. 3. В схеме, полученной в п. 1.1, исключить (замкнуть) все источники кроме 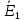 и рассчитать, используя простые преобразования цепей, ток в цепи источника и рассчитать, используя простые преобразования цепей, ток в цепи источника 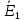 . По результатам расчета построить векторную диаграмму для цепи, в которой все элементы цепи, кроме резистора R, подключенного к источнику . По результатам расчета построить векторную диаграмму для цепи, в которой все элементы цепи, кроме резистора R, подключенного к источнику 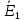 , объединены в эквивалентное сопротивление , объединены в эквивалентное сопротивление 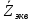 , как показано на рисунке 2. , как показано на рисунке 2.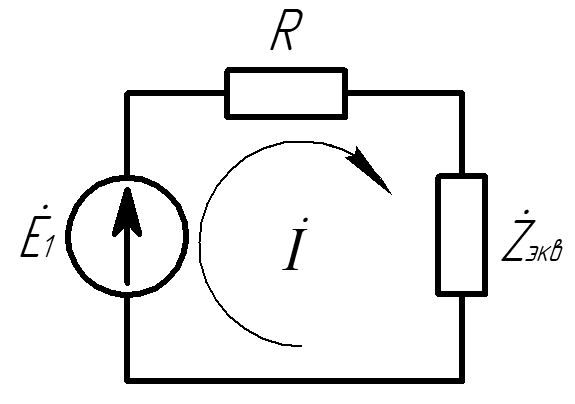 Рисунок 2 - Схема эквивалентной цепи Осуществить моделирование цепи с помощью программы EWB-5.12 и определить значение тока в цепи источника 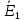 , а также напряжения на сопротивлении , а также напряжения на сопротивлении 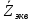 и R. и R.1.4. Используя схему из п. 1.1, рассчитать токи и напряжения на ее элементах, используя формулы Крамера, а также обращение матриц. Осуществить сравнение результатов. 1.5. Для схемы из п. 1.3 найти выражение для комплексного коэффициента передачи электрической цепи. 1.6. Используя формулу для комплексного коэффициента передачи цепи определить выражение для АЧХ и ФЧХ цепи. 1.7. Построить, используя выражения из п. 1.6, графики для АЧХ и ФЧХ цепи. 1.8. Определить граничные частоты полосы пропускания и коэффициент прямоугольности цепи, используя результаты п. 1.7. 1.9. Дать характеристику исследуемой цепи по п. 1.3 с точки зрения фильтрации электрических колебаний. Содержание 1 Первый этап. Представление в двоичном коде номера варианта и схемы..................6 2 Второй этап. Расчет простой электрической цепи..........................................................8 2.1 Упрощение схемы и составление формул для простой электрической цепи.......................................................................................................................................8 2.2 Построение векторной диаграммы...................................................................11 3 Третий этап. Расчет сложной электрической цепи......................................................13 3.1 Расчет сложной электрической цепи методом Крамера.................................16 3.2 Расчет сложной электрической цепи методом обращения матриц................27 4 Четвертый этап................................................................................................................21 4.1 Определение выражения для комплексного коэффициента передачи цепи для схемы............................................................................................................................21 4.2 Построение АЧХ и ФЧХ цепи с указанием граничных частот и коэффициента прямоугольности......................................................................................24 Заключение.........................................................................................................................28 Список литературы............................................................................................................29 Приложение........................................................................................................................30 Приложение А. Расчет простой цепи в Mathcad 15...............................................30 Приложение Б. Схема простой цепи в EWB-5.12.................................................31 Приложение В. Расчет контурных токов сложной цепи в Mathcad с помощью формулы Крамера..............................................................................................................32 Приложение Г. Расчет контурных токов сложной цепи в Mathcad методом обращения матриц .............................................................................................................33 Приложение Д. Схема сложной цепи в EWB-5.12................................................34 Приложение Е. Вывод формул контурных токов для нахождения коэффициента передачи..............................................................................................................................35 1 Первый этап. Представление в двоичном коде номера варианта и схемы Для выбора схемы необходимо представить свой номер по журналу в двоичной форме. Мой номер варианта по журналу 16. Установим переключатели К1- К5 в положения, соответствующие номеру 16 в двоичной записи. Таблица 1 – Положение ключей в схеме
Зарисуем получившуюся схему без переключателей и отсоединенных элементов. 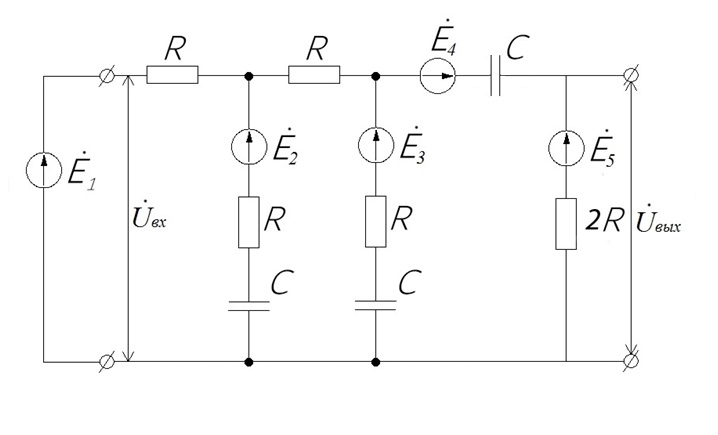 Рисунок 4 – Схема с замкнутыми переключателями Определим величины элементов схемы (рисунок 4) по формулам (1), (2), (3), (4), учитывая, что все генераторы в схеме имеют одинаковую частоту. R = 100 · [4 + 0,2 · 16] = 720 [Ом]; С = 100 · [5 + 0,2 · 18] = 820 [пФ] = 820·10-12 [Ф]; 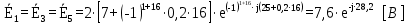 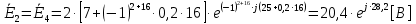 f1 = 10·[7+(-1)16·0,2·16] = 102 [кГц] = 102·103 [Гц] Значение фазы источников 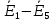 задается в градусах, а Mathcad осуществляет расчеты в радианах. Вследствие этого при вычислениях величину фазы задается в градусах, а Mathcad осуществляет расчеты в радианах. Вследствие этого при вычислениях величину фазы 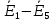 будем умножать на величину будем умножать на величину 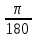 . .2 Второй этап. Расчет простой электрической цепи 2.1 Упрощение схемы и составление формул для простой электрической цепи Замкнем все источники в схеме, кроме 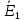 (рисунок 5). (рисунок 5).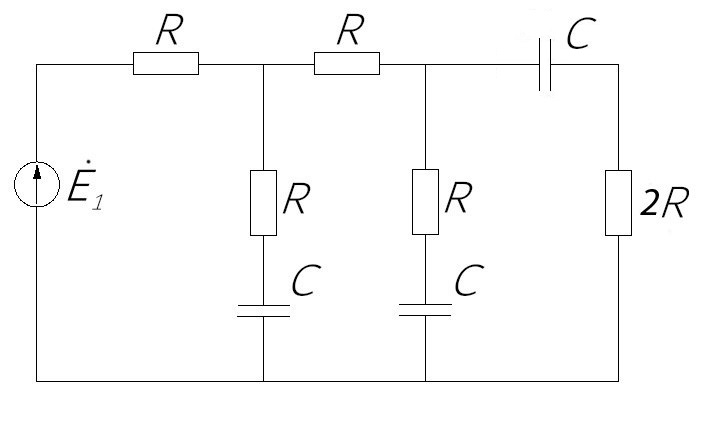 Рисунок 5 - Схема простой цепи с замкнутыми источниками 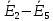 Преобразуем данную схему, объединив все элементы цепи, кроме R, подключенного к источнику Ė1, в эквивалентное сопротивление 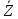 экв эквРассчитаем, используя простые преобразования цепей, ток в цепи источника Ė1, а также напряжения на R и 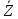 экв. экв.Значение тока в цепи источника определяется по формуле: 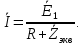 (5) (5)Эквивалентное сопротивление 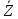 экв определим, используя формулы для последовательного и параллельного соединения нескольких элементов. Значение сопротивления конденсатора экв определим, используя формулы для последовательного и параллельного соединения нескольких элементов. Значение сопротивления конденсатора 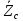 определяется по формуле (6): определяется по формуле (6):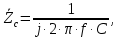 (6) (6)где j – мнимая единица, π – математическая постоянная, f - частота, C – ёмкость конденсатора. Сопротивления 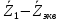 находят по формулам последовательного и параллельного соединения (7) и (8): находят по формулам последовательного и параллельного соединения (7) и (8):1) Последовательное соединение: R = R1 + R2; (7) 2) Параллельное соединение: 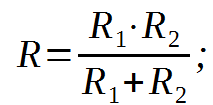 (8) (8)Значения сопротивлений 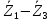 исходя из преобразований на рисунке 6 будут равны: исходя из преобразований на рисунке 6 будут равны: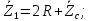 (9) (9)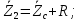 (10) (10)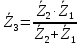 . (11) . (11)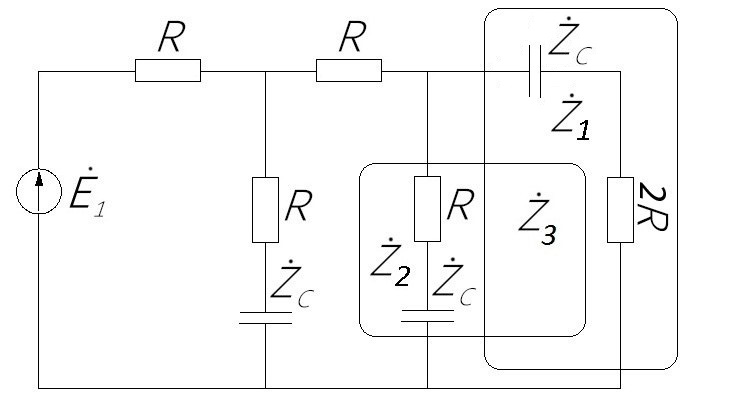 Рисунок 6 – Сопротивления 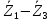 Значения сопротивлений 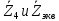 после преобразований на рисунке 7 будут равны: после преобразований на рисунке 7 будут равны: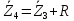 ;(12) ;(12)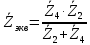 . (13) . (13)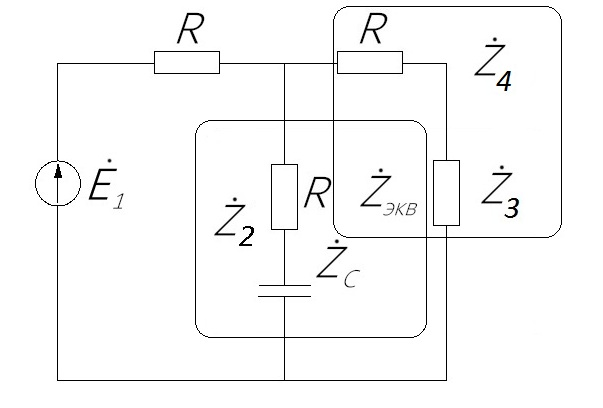 Рисунок 7 – Сопротивления 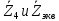 Напряжение на сопротивлении R определяется по формуле (14) 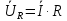 . (14) . (14)Напряжение на сопротивлении 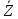 экв определяется по формуле (15) экв определяется по формуле (15)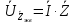 экв. (15) экв. (15)Все необходимые расчеты проведем в среде Mathcad (Приложение А). 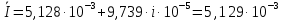 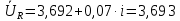 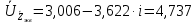 2.2 Построение векторной диаграммы По полученным значениям строим векторную диаграмму в масштабе для 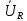 , , 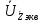 , ,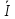 , Ė1, имея в виду, что в цепи выполняется второй закон Кирхгофа, т.е. , Ė1, имея в виду, что в цепи выполняется второй закон Кирхгофа, т.е. 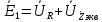 , а для векторов это отражается в виде их векторной суммы. Для построения векторной диаграммы запишем значения тока , а для векторов это отражается в виде их векторной суммы. Для построения векторной диаграммы запишем значения тока 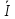 , напряжений , напряжений 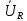 , , 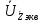 и источника Ė1 в показательной форме, т.е. и источника Ė1 в показательной форме, т.е.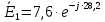 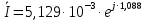 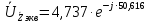 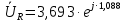 Расчеты аргументов 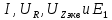 также проведем в среде Mathcad (Приложение А). также проведем в среде Mathcad (Приложение А).Построим векторную диаграмму. 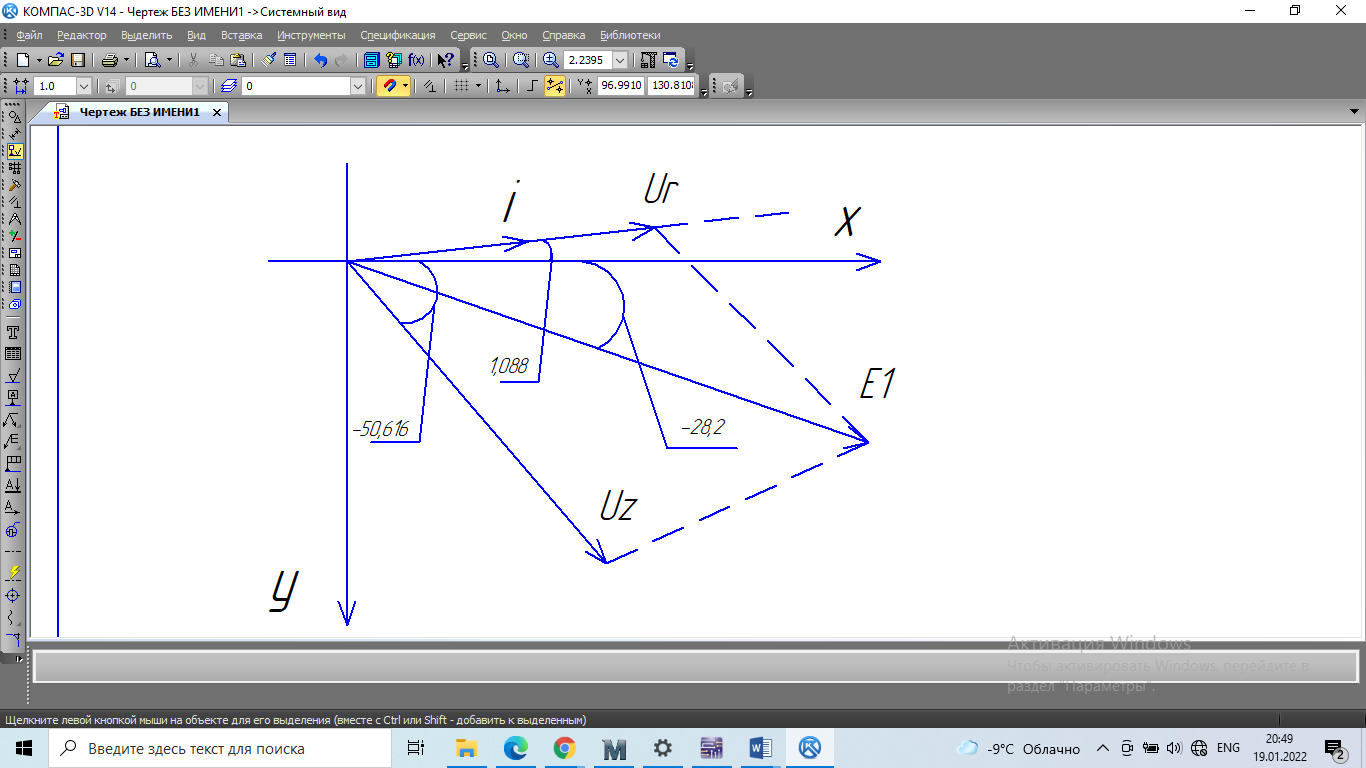 Рисунок 8 - Векторная диаграмма 3 Третий этап. Расчёт сложной электрической цепи Для определения токов и напряжений на всех элементах цепи при известных значениях R, C и E необходимо составить систему уравнений по методу контурных токов. 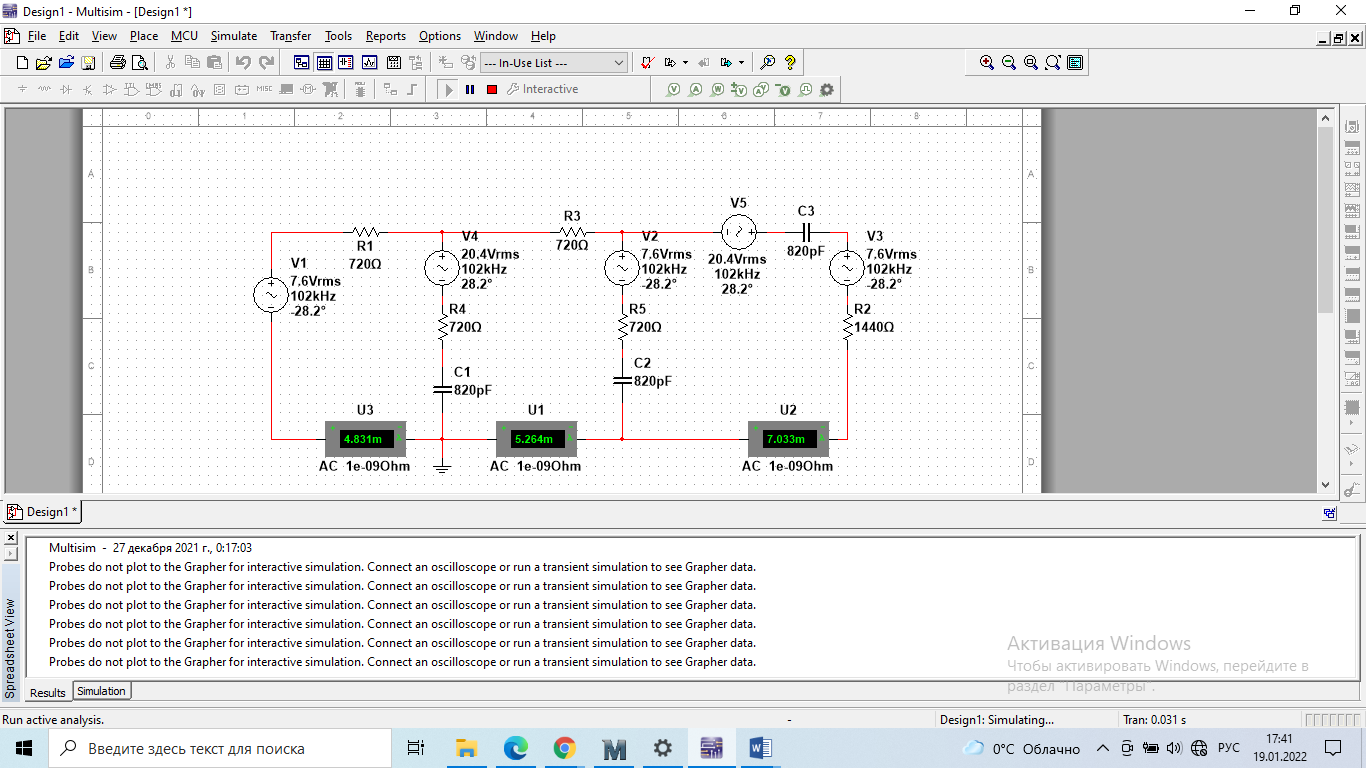 Рисунок 9 - Сложная электрическая цепь Вначале составляется граф данной электрической цепи, по которому выбираются независимые контуры и задаются контурные токи. 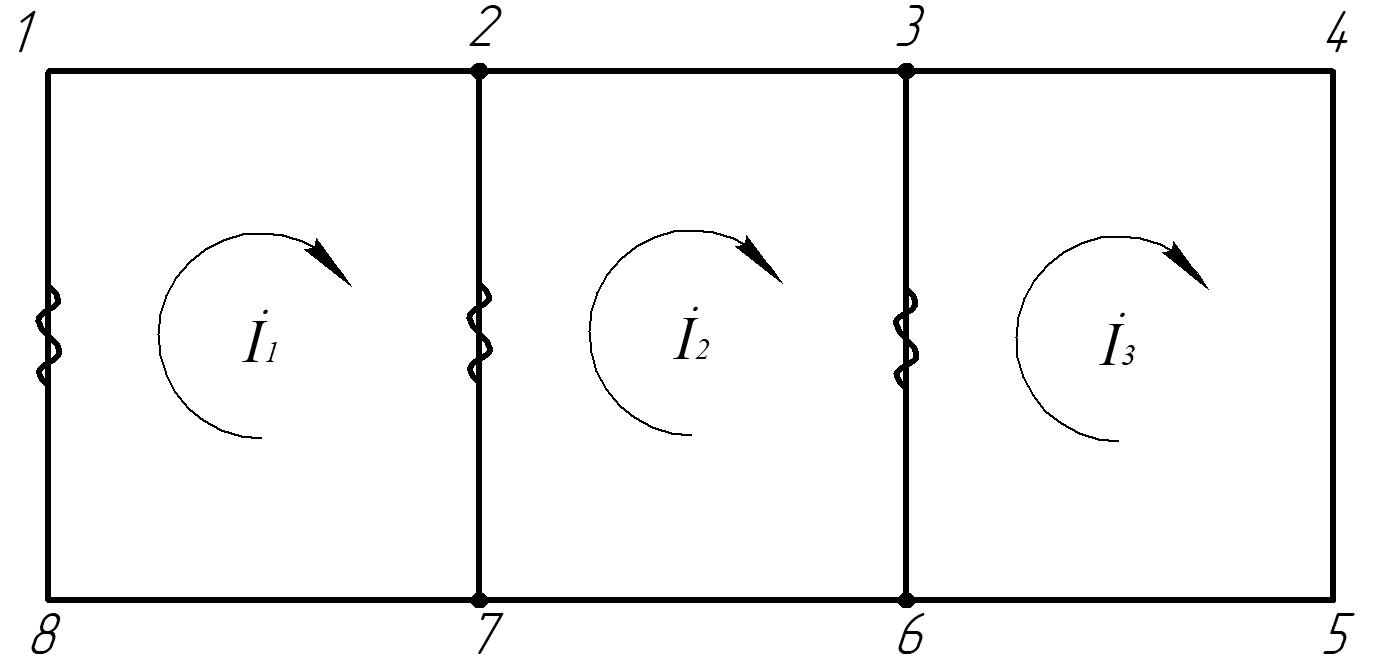 Рисунок 10 – Граф сложной электрической цепи Независимые контуры: 12781, 23672, 34653. Следовательно, система уравнений будет содержать три независимых уравнения. Проверим количество уравнений через количество узлов и ветвей цепи. Первый закон Кирхгофа имеет отношение к узлам цепи. Второй закон Кирхгофа к контурам. Если электрическая цепь содержит m узлов, то число уравнений, которые надо составить по первому закону Кирхгофа определяется как 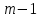 . .Если электрическая цепь содержит n ветвей, то число уравнений, которые надо составить по второму закону Кирхгофа определяется как 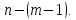 В моей электрической цепи количество узлов 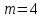 , количество ветвей , количество ветвей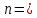 6. Следовательно для моей цепи надо составить 6. Следовательно для моей цепи надо составить 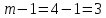 уравнения по первому закону Кирхгофа и уравнения по первому закону Кирхгофа и 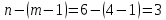 уравнения по второму закону Кирхгофа. уравнения по второму закону Кирхгофа.Преобразуем элементы электрической схемы, воспользовавшись формулами для последовательного и параллельного соединения нескольких элементов. 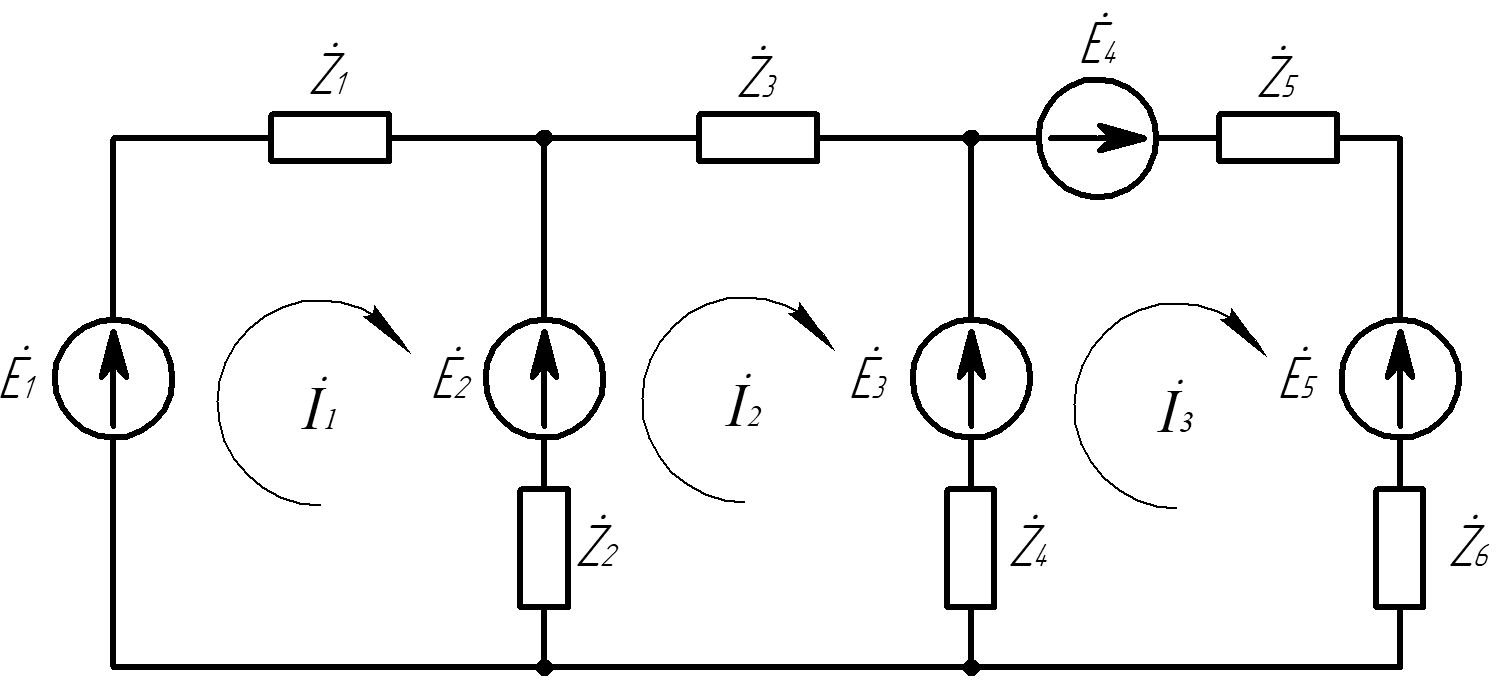 Рисунок 11 – Обозначение элементов 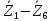 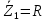 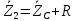 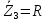 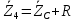 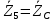 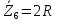 Получим систему, состоящую из трех независимых уравнений: 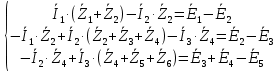 (16) (16)Теперь переменные 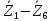 будут иметь новые значения: будут иметь новые значения: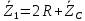 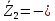 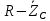 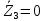 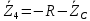 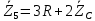 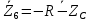 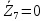 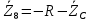 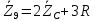 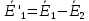 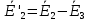 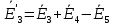 3.1 Расчёт сложной электрической цепи методом Крамера Исходя из системы уравнений, вначале составим матрицу сопротивлений, т.е. выписываем соответствующие коэффициенты при токах 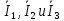 . .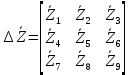 (17) (17)Затем по матрице найдем ее частичные определители: 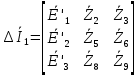 ; (18) ; (18)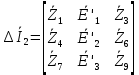 ; (19) ; (19)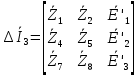 . (20) . (20)Контурные токи определяются по формулам Крамера: 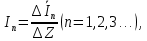 (21) (21)где 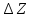 – полный определитель матрицы; – полный определитель матрицы;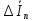 – определитель из – определитель из 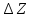 , получающийся при замене его элементов к-го столбца соответствующими правыми частями уравнения. , получающийся при замене его элементов к-го столбца соответствующими правыми частями уравнения.Расчеты произведены в среде Mathcad (Приложение В): Для сравнения с результатами, полученными в EWB-5.12, найдем аргументы 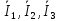 (Приложение В): (Приложение В):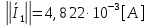 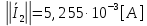 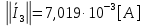 3.2 Расчет токов и напряжений в сложной электрической цепи методом обращения матрицы Представим систему уравнений в матричной форме: 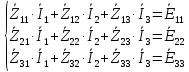 , (22) , (22)где 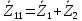 ; ;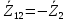 ; ; 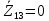 ; ; 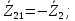 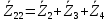 ; ; 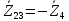 ; ; 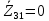 ; ; 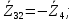 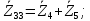 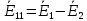 ; ; 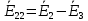 ; ;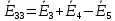 . .Уравнения можно записать в виде произведения матриц 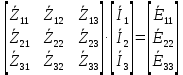 . (22) . (22)или в сокращенном варианте как: 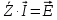 , (23) , (23)где 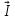 - вектор-столбец токов; - вектор-столбец токов;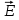 - вектор-столбец напряжений. - вектор-столбец напряжений.Если 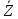 - квадратная матрица и ее определитель отличен от нуля, то существует такая обратная матрица - квадратная матрица и ее определитель отличен от нуля, то существует такая обратная матрица 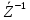 , что , что 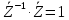 Умножив уравнение 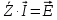 слева и справа на обратную матрицу слева и справа на обратную матрицу 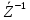 , получим, что , получим, что 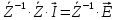 . . Принимая во внимание 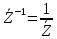 , получим: , получим: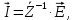 (24) (24)где 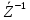 - обращенная матрица комплексных сопротивлений схемы, состоящая из коэффициентов: - обращенная матрица комплексных сопротивлений схемы, состоящая из коэффициентов: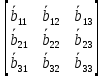 . (25) . (25)Значения контурных токов 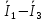 определяются через формулы определяются через формулы 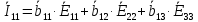 ; (26) ; (26)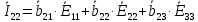 ; (27) ; (27)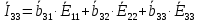 ; (28) ; (28)Таким образом, для вычисления неизвестных токов 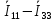 необходимо определить коэффициенты необходимо определить коэффициенты 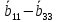 обратной матрицы обратной матрицы 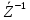 и осуществить их подстановку в уравнение. и осуществить их подстановку в уравнение.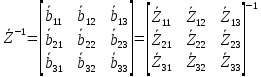 . (29) . (29)Расчеты произведем в среде Mathcad (Приложение Г). Используя EWB-5.12, соберем схему сложной цепи (Приложение Д). Сравним результаты, полученные методом Крамера и методом обращения матрицы: 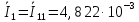  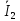 = =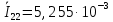 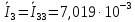 Результаты равны, сравнения значений тока с EWB-5.12 представлены в таблице 3. Таблица 3 - Сравнение результатов сложной схемы
4. Четвёртый этап. 4.1 Определение выражения для комплексного коэффициента передачи В соответствии с определением комплексный коэффициент передачи 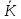 схемы определяется: схемы определяется: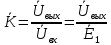 . (30) . (30)Напряжение 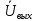 определим, используя метод контурных токов. Преобразуем схему (рисунок 12): определим, используя метод контурных токов. Преобразуем схему (рисунок 12):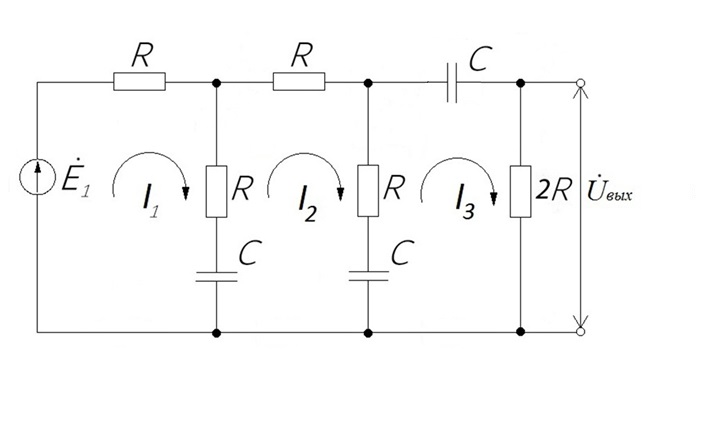 Рисунок 12 - Схема цепи для определения 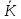 Составим систему уравнений по методу контурных токов: 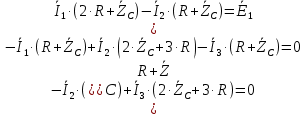 . (31) . (31)Выразим из первого уравнения ток 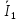 и подставим его во второе уравнение, из второго уравнения выразим ток и подставим его во второе уравнение, из второго уравнения выразим ток 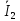 и подставим его в третье уравнение, из которого найдем ток и подставим его в третье уравнение, из которого найдем ток 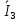 . .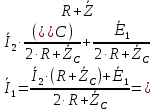 ; (32) ; (32)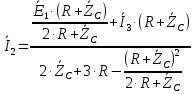 ; (33) ; (33)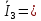 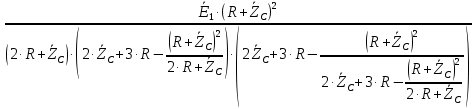 ; (34) ; (34)Напряжение на выходе цепи 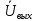 в схеме (Рисунок 10) равно в схеме (Рисунок 10) равно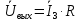 (35) (35)Определение выражения для комплексного коэффициента передачи методом обращения матрицы сопротивлений 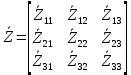 ; (36) ; (36)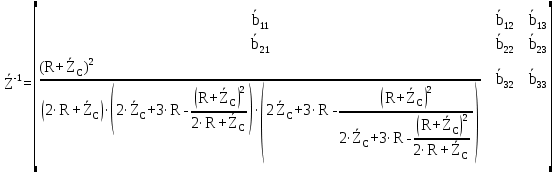 ; (37) ; (37)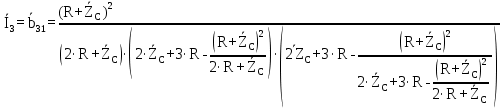 . (38) . (38)Сравним выражения комплексного коэффициента передачи, полученного по обращения матрицы и по методу контурных токов. Комплексный коэффициент передачи, полученный по методу контурных токов, равен: 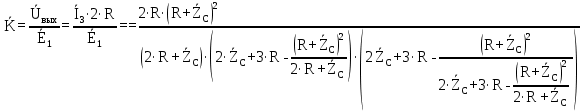 . (39) . (39)Комплексный коэффициент передачи, полученный по методу обращения матрицы сопротивлений, равен: 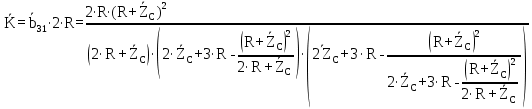 . (40) . (40)Уравнения комплексного коэффициента передачи, полученные обоими способами равны. 4.2 Построение графиков АЧХ и ФЧХ (Mathcad и EWB 5.12) с определением их характеристик Для построения амплитудно-частотной характеристики определим выражение для АЧХ: 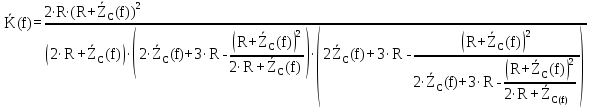 (41) (41)Для построения фазо-частотной характеристики (ФЧХ) определим аргумент комплексного коэффициента передачи 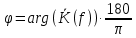 После определения выражений для АЧХ и ФЧХ необходимо осуществить построение их графиков с использованием соответствующих операций из программы Mathcad (рисунки 13 и 14) 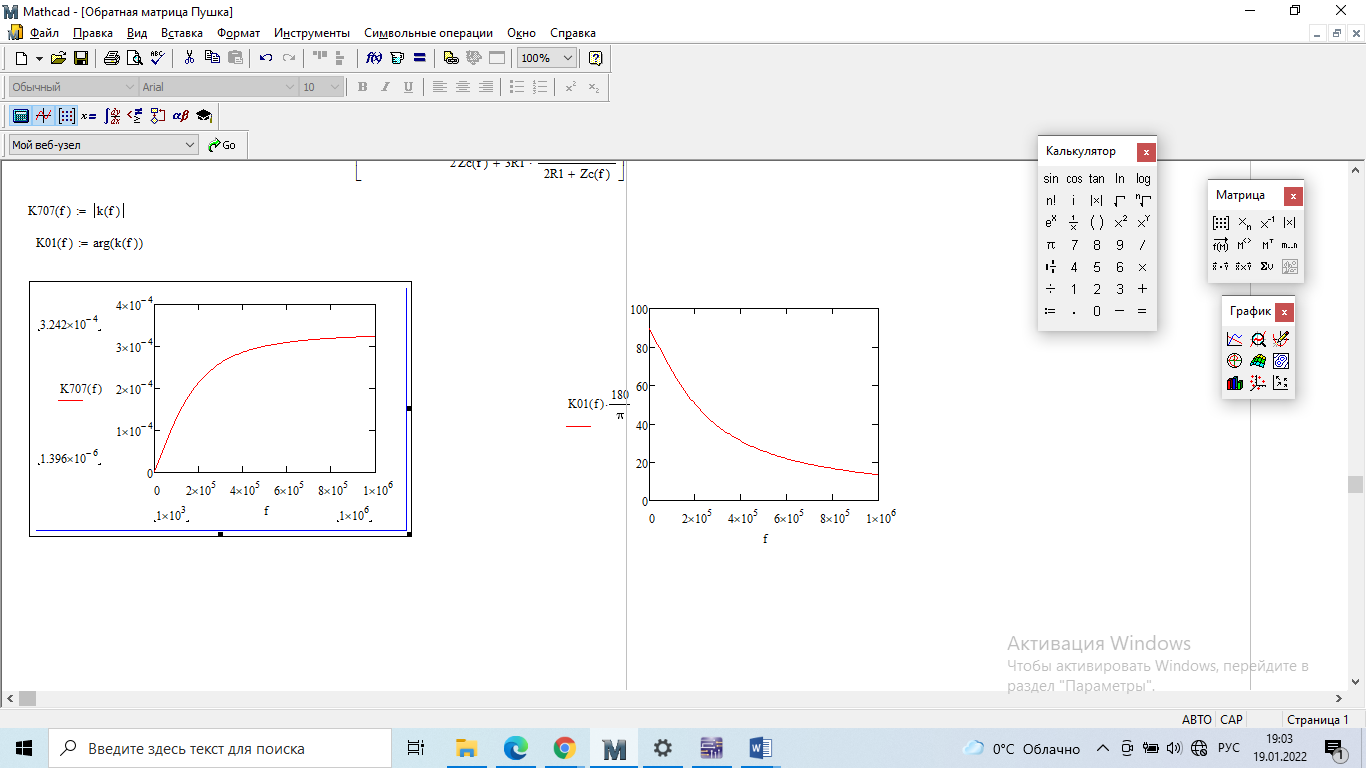 Рисунок 13 – Амплитудно-частотная характеристика цепи 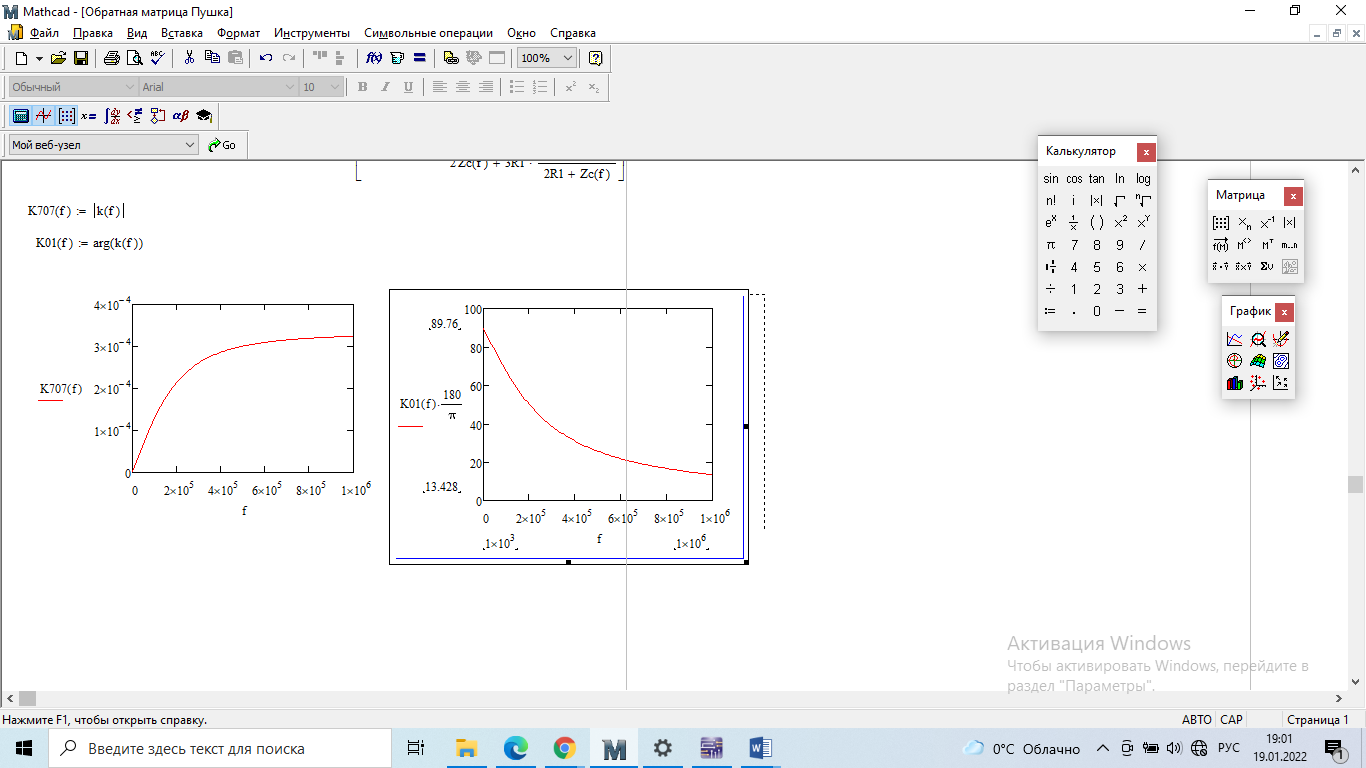 Рисунок 14 – Фазо-частотная характеристика цепи При анализе АЧХ и ФЧХ цепи установим значения R=1000 Ом, С= 1 нФ = 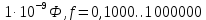 , частоту изменений с интервалом 100 Гц. , частоту изменений с интервалом 100 Гц.Для сравнения построим АЧХ и ФЧХ, используя программный симулятор EWB-5.12 (рисунок 15 и 16). Рисунок 15 – Схема для определения АЧХ и ФЧХ Для вычисления коэффициента прямоугольности воспользуемся формулой 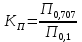 , (42) , (42)где 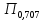 – полоса частот по уровню сигнала – полоса частот по уровню сигнала 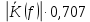 , ,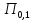 – полоса частот по уровню сигнала – полоса частот по уровню сигнала 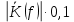 . .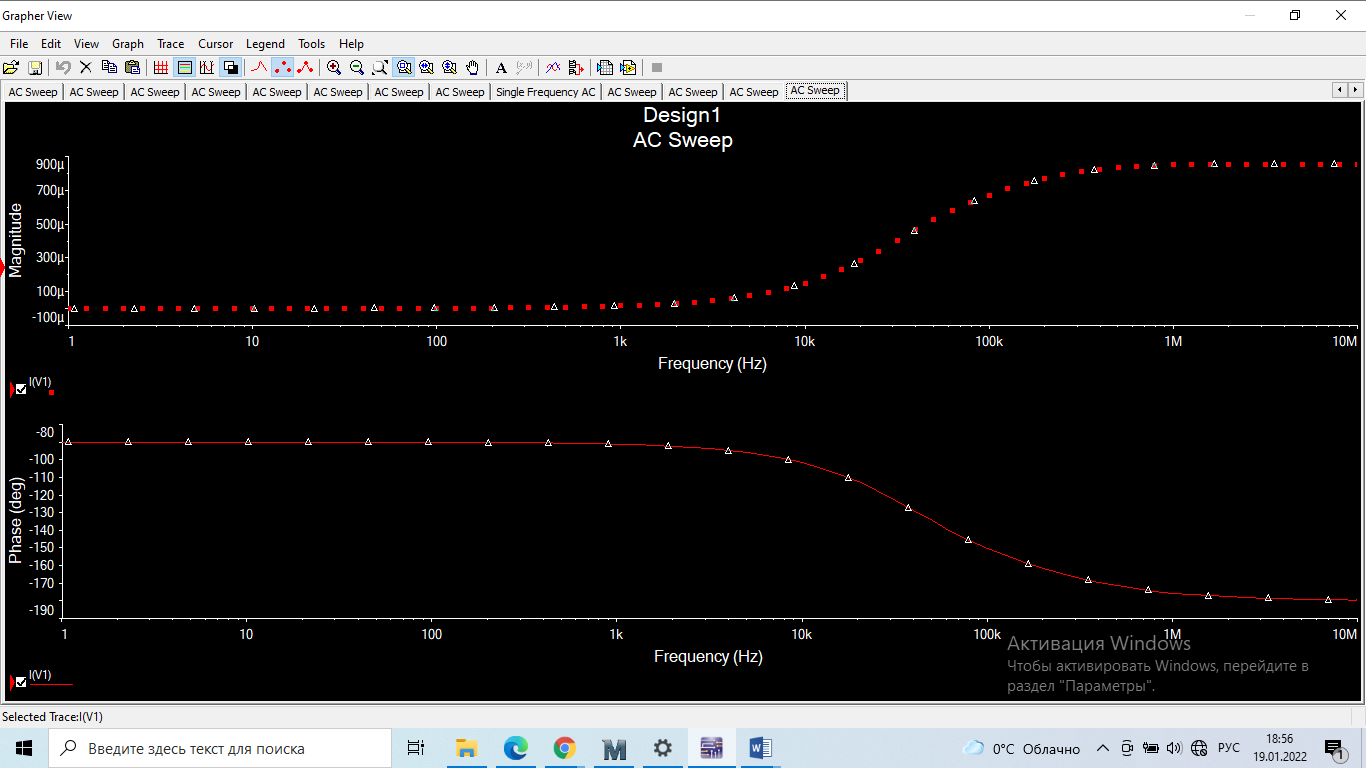 Рисунок 16 – Результат АЧХ и ФЧХ в EWB-5.12 Используя построенный график АЧХ в Mathcad, определим 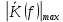 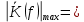 0,3 [В] 0,3 [В]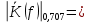 0,267 [B] 0,267 [B]что соответствует fгр1= 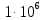 [Гц] [Гц]fгр2= 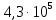 [Гц] [Гц]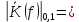 0,1 [B] 0,1 [B]что соответствует f1= 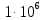 [Гц] [Гц] f2= 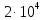 [Гц] [Гц]Таким образом, полоса частот по уровню 0,707: П0,707 = fгр1- fгр2= 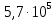 [Гц] [Гц]Полоса частот по уровню 0,1: П0,1 = fгр1- fгр2= 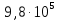 [Гц] [Гц]Вычислим коэффициент прямоугольности по формуле 42: 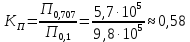 Данная цепь с точки зрения фильтрации колебаний, является интегрирующей RC-цепью. Она обеспечивает прохождение высоких частот в диапазоне от 57 кГц, а низкие «заваливает», то есть является фильтром высоких частот (ФВЧ). Заключение В процессе выполнения курсовой работы мы освоили методы расчета схем с использованием вычислительной техники, компьютерного схемотехнического моделирования и экспериментальных исследований электрических цепей На основе полученных знаний в процессе выполнения курсовой работы мы освоили следующие темы дисциплины "Общая электротехника и электроника": переходные процессы, цепи гармонического тока; частотноизбирательные цепи; методы расчетов электрических цепей; электрические фильтры. Все это обеспечивает студентов необходимой подготовкой для предстоящих инженерных исследований. Список литературы Методические указания к курсовой работе «Расчет линейной электрической цепи при гармоническом воздействии» / ФБОУ ВО «Воронежский государственный технический университет»; сост.: Б. В. Матвеев, В. Н. Поветко, И. И. Малышев – Воронеж: Изд-во ВГТУ, 2018. 20 с. Матвеев Б. В. Общая электротехника и электроника: учеб. пособие. Часть 1. Линейные электрические цепи / Воронеж: ГОУВПО «Воронежский государственный технический университет», 2006. 241 с. Электротехника. В 2 ч. Часть 1: учеб, пособие для академического бакалавриата / под ред. 10. Л. Хотунцева. — 3-е изд., перераб, и доп. М.: Издательство Юрайт, 2019. 243 с. Электротехника и электроника: Учебник для сред. проф. образования / Б. И. Петленко, Ю. М. Иньков, А. В. Крашенинников и др.; Под ред. Б. И. Петленко. — М.; Издательский центр, «Академия». 2003. 320 с. Приложение А Вычисления в Mathcad Приложение Б Схема простой цепи в EWB-5.12 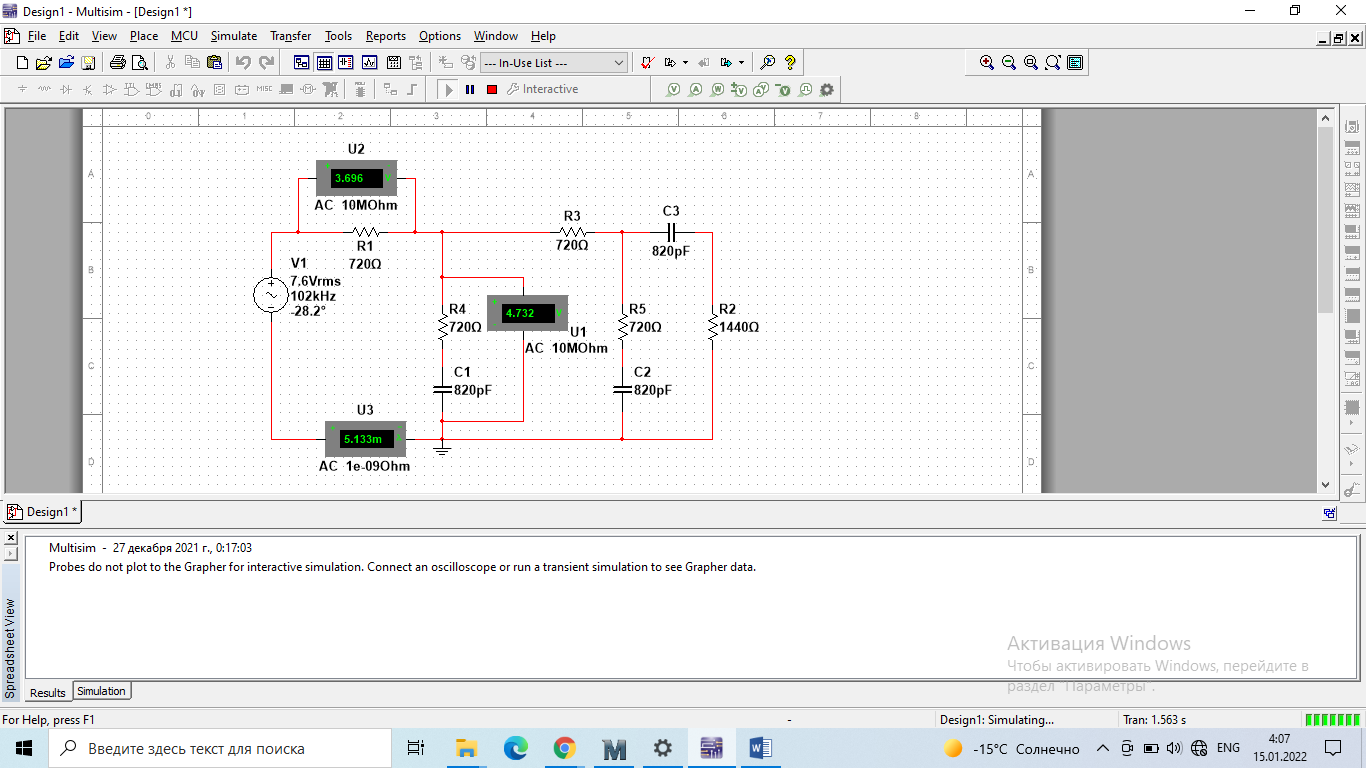 Приложение В Расчет контурных токов сложной цепи в Mathcad с помощью формулы Крамера        Приложение Г Расчет контурных токов сложной цепи в Mathcad методом обращения матрицы   Приложение Д Схема сложной цепи в EWB-5.12  |

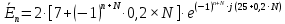 [В];
[В];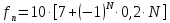 [кГц],
[кГц],