МЖГ Решение мат модели 7. Курсовая работа по дисциплине Теория и расчёт лопаточных машин На тему Турбина силовая
 Скачать 0.94 Mb. Скачать 0.94 Mb.
|
МАТЕМАТИЧЕСКАЯ МОДЕЛЬДля описания вихря используется уравнение Эйлера: где Ускорение от массовых сил есть сумма ускорений от сил тяжести и центробежного ускорения: Центробежное ускорение определяется следующим выражением: Закон постоянства циркуляции: Для связи давления с осевой и окружной скоростями применяется уравнение Бернулли: Для дальнейших расчетов уравнение Бернулли (6) делится на dr, в результате уравнение примет вид: Для нахождения распределения температуры по радиусу используется тепловое уравнение энергии: Аналогично данное уравнение следует разделить на dr, в результате получается: РЕШЕНИЕВектор свободного перемещения имеет вид: Для перехода от частных дифференциалов к полным уравнение Эйлера (2) умножается скалярно на вектор свободного перемещения: Подставляя (12) и (13) в (2), можно получить уравнение Эйлера в нужном виде: Из (5) окружную скорость можно представить в следующем виде: Центробежное ускорение с учётом (4) и (15) примет вид: Подставив (16) в (14), получается следующее уравнение: Для последующего интегрирования уравнение (17) преобразовывается к виду: Далее производится интегрирование левой и правой части уравнения (18): 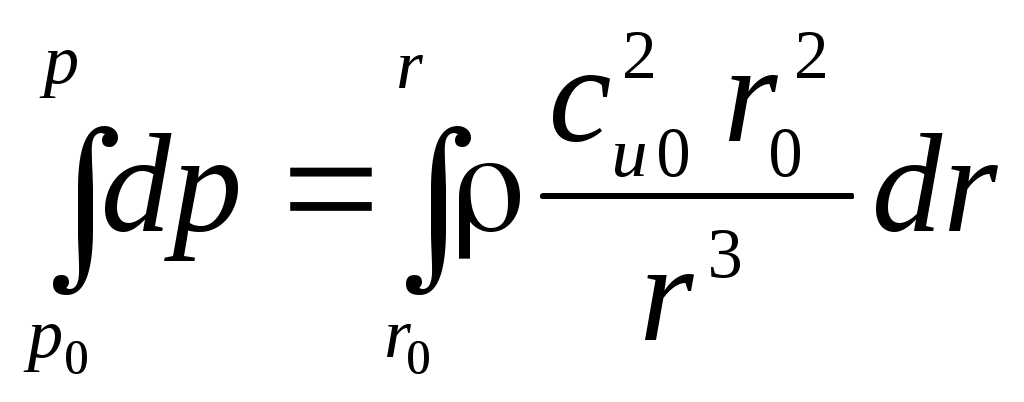 , (19.1) , (19.1)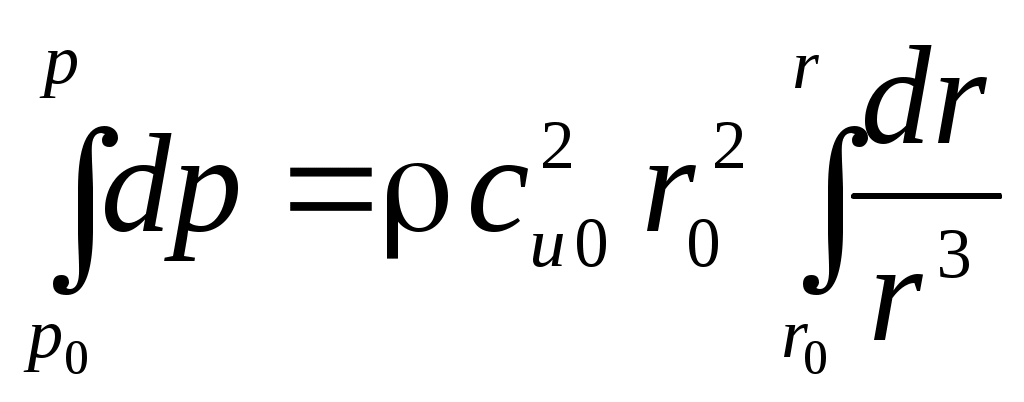 , (19.2) , (19.2)В результате зависимость давления от радиуса имеет вид: 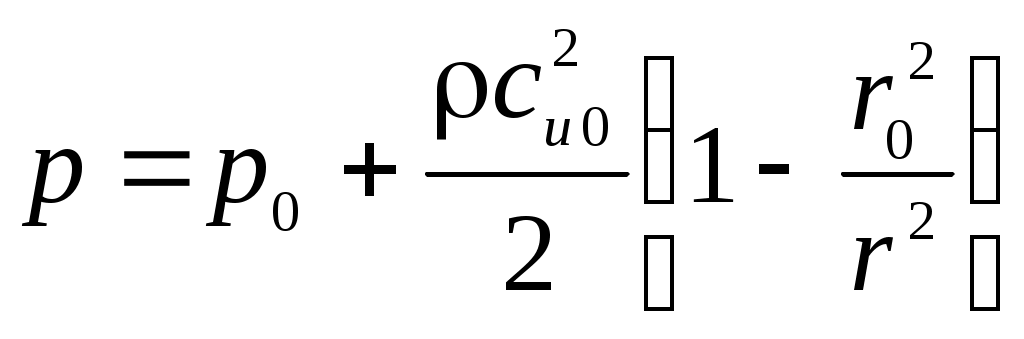 . (20) . (20)При Подставив (21) в (20), получается выражение для функции r: Для определения зависимости осевой составляющей скорости от радиуса необходимо воспользоваться уравнением Бернулли. Выражения (17) и (15) подставляются в уравнение Бернулли (7): 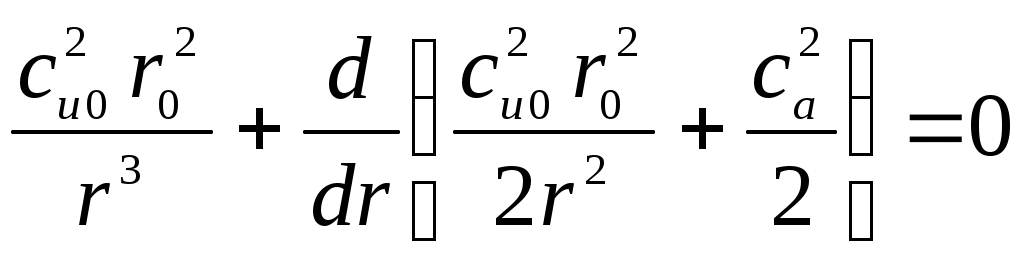 . (23) . (23)После умножения на dr уравнение (23) примет вид: 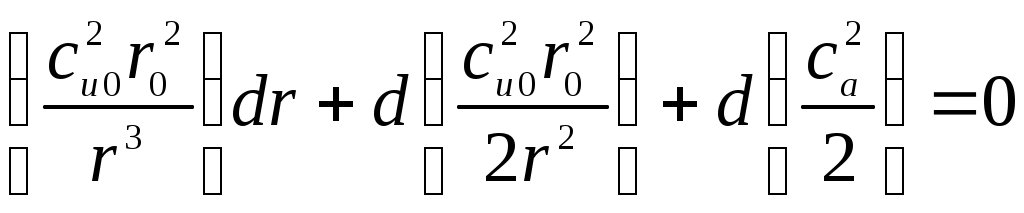 . (24) . (24)Второе слагаемое преобразуется к виду: 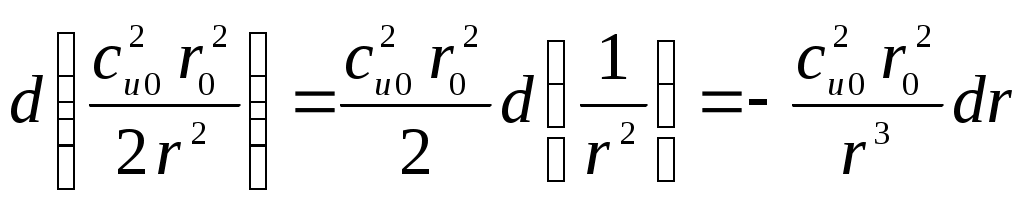 . (25) . (25)С учетом (25) уравнение (24) примет вид: Из выражения (26) следует, что ca не зависит от радиуса, т.е. осевая составляющая скорости постоянна. Для определения зависимости температуры от радиуса необходимо воспользоваться уравнением энергии (9). Второе слагаемое уравнения (9) можно записать с учётом (25) и (26) в следующем виде: Тогда уравнение (9) c учетом (26) примет вид: Уравнение (28) умножается на dr, далее решается интегральное уравнение: 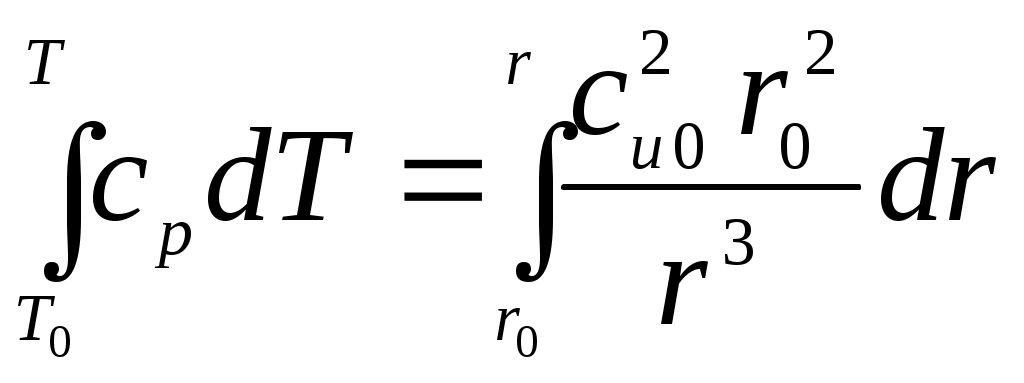 , (29.2) , (29.2)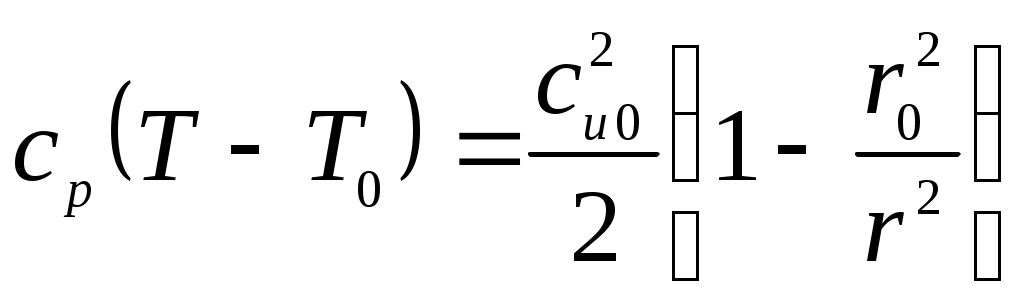 . (29.4) . (29.4) Из уравнения (29.4) выражается функция зависимость температуры от радиуса: 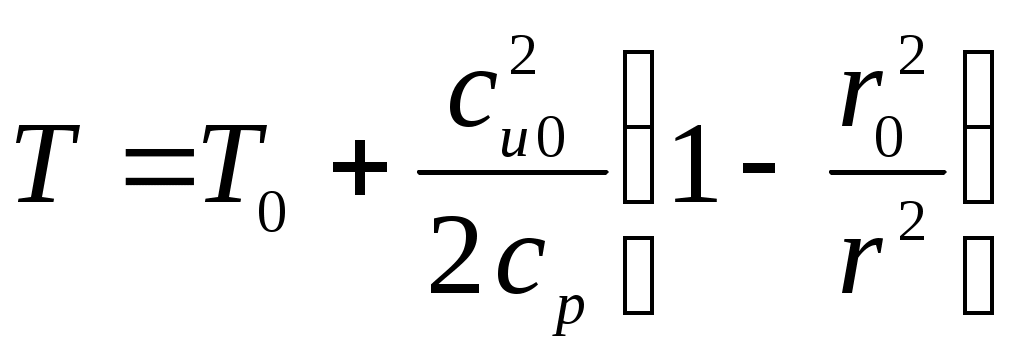 . (30) . (30)При Подставляя (31) в выражение (30), получается выражение для функции T(r): |
