МЖГ Решение мат модели 7. Курсовая работа по дисциплине Теория и расчёт лопаточных машин На тему Турбина силовая
 Скачать 0.94 Mb.
|
Решение задачи по математической моделиДля наибольшей наглядности решения задачи рассчитаем параметры воздуха в центре вихря, при условии что  , также дополнительно зададим области, незахваченные вихрем. Пусть начальные условия будут следующие:      Тогда можем определить параметры воздуха в центре вихря:   Анализ результатовПроанализируем температуры, распределения давлений и окружную скорость вдоль радиуса. Воспользуемся полученными уравнениями (15), (20), (30). С помощью Microsoft Excel построим графики и таблицы Анализ адекватности Каких-либо неадекватных результатов не наблюдается, отметим только то, что не была рассмотрена задача в центре вихря при  . Здесь, ближе к центру, окружная скорость cu стремится к бесконечности, так как полученная зависимость (15) обратно пропорциональная, даже если осевая скорость cа и уходит в ноль.То есть задача решаема только при бесконечно большой кинетической энергии Eкин, что неадекватно, следовательно, необходимо ограничить область применимости. Так как центр будет вращаться по другому закону, то cu будет меняться по линейному закону («закон твердого тела»), если учесть, что существует некая переходная зона, то физически задача реальна Анализ изменения давления и температуры по радиусу Согласно расчётам, которые представлены в пункте «Решение математической задачи» давление вблизи центра вихря принимает значение  , а температура  . Такие значения вполне реальны и соответствуют, например, буре.Расчёт вихря вдоль радиуса показывает, что по мере увеличения радиуса, уменьшается интенсивность изменения параметров. А при параметры стремятся к атмосферным.Область применимости Как было сказано ранее, решение не работает при . Если при намечается зона, где работает закон постоянства циркуляции, то в той зоне, работает другой закон, закон твердого тела.Полученное решение применимо для вихря, происходящего без диссипации, за пределами зоны, где происходит вращение по закону твёрдого тела. ЗаключениеПо работе можно сделать следующие выводы: 1. Выяснено, что вихрь вращается по двум законам: закону постоянства циркуляции за границей ядра вихря и по закону твёрдого тела внутри ядра. 2. Из анализа численных данных, полученных путём применения математического решения по данным условиям, понятно, что решение является адекватным и достоверным, есть соответствие реальным процессам. 3. Решение имеет свою область применимости для окружной скорости: на произвольном радиусе закон постоянства циркуляции работает лишь за пределами зоны вращения по закону твёрдого тела. 4. Возникает еще одна задача о вращении при приближении к центру, при этом считая, что переходную зону можно свести к нулю – законы перетекают сменяют друг друга мгновенно. 5. Путём сопоставления значений за пределами вихря, то есть атмосферные, с полученными вблизи центра, получено представление о глубине разряжения и охлаждения:  ; .Приложение А Результаты вычислений Таблица 1 Параметры свободного вихря
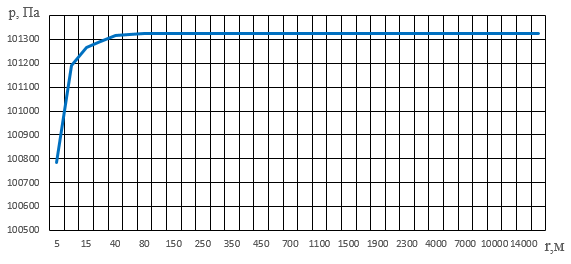 Рис. А. 1. График зависимости давления от радиуса 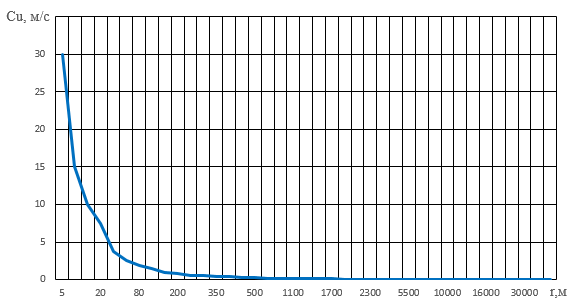 Рис. А. 2. График зависимости окружной скорости от радиуса 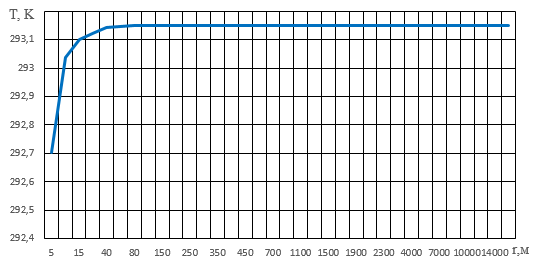 Рис. А. 3. График зависимости температуры от радиуса |