доп билеты. 29. Интегрирование уравнения Эйлера для потенциального потока
 Скачать 5.26 Mb. Скачать 5.26 Mb.
|
|
29.Интегрирование уравнения Эйлера для потенциального потока. 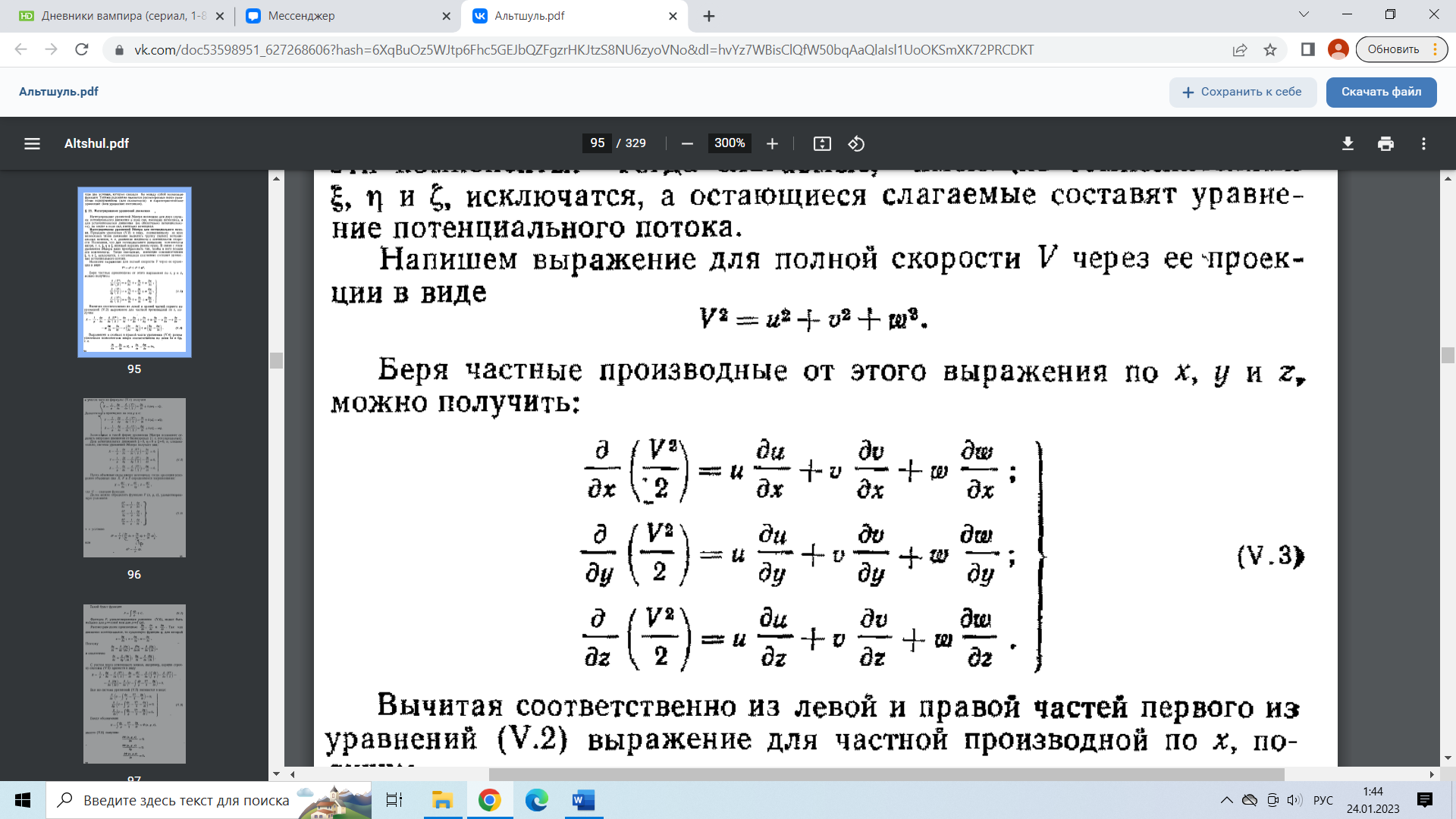 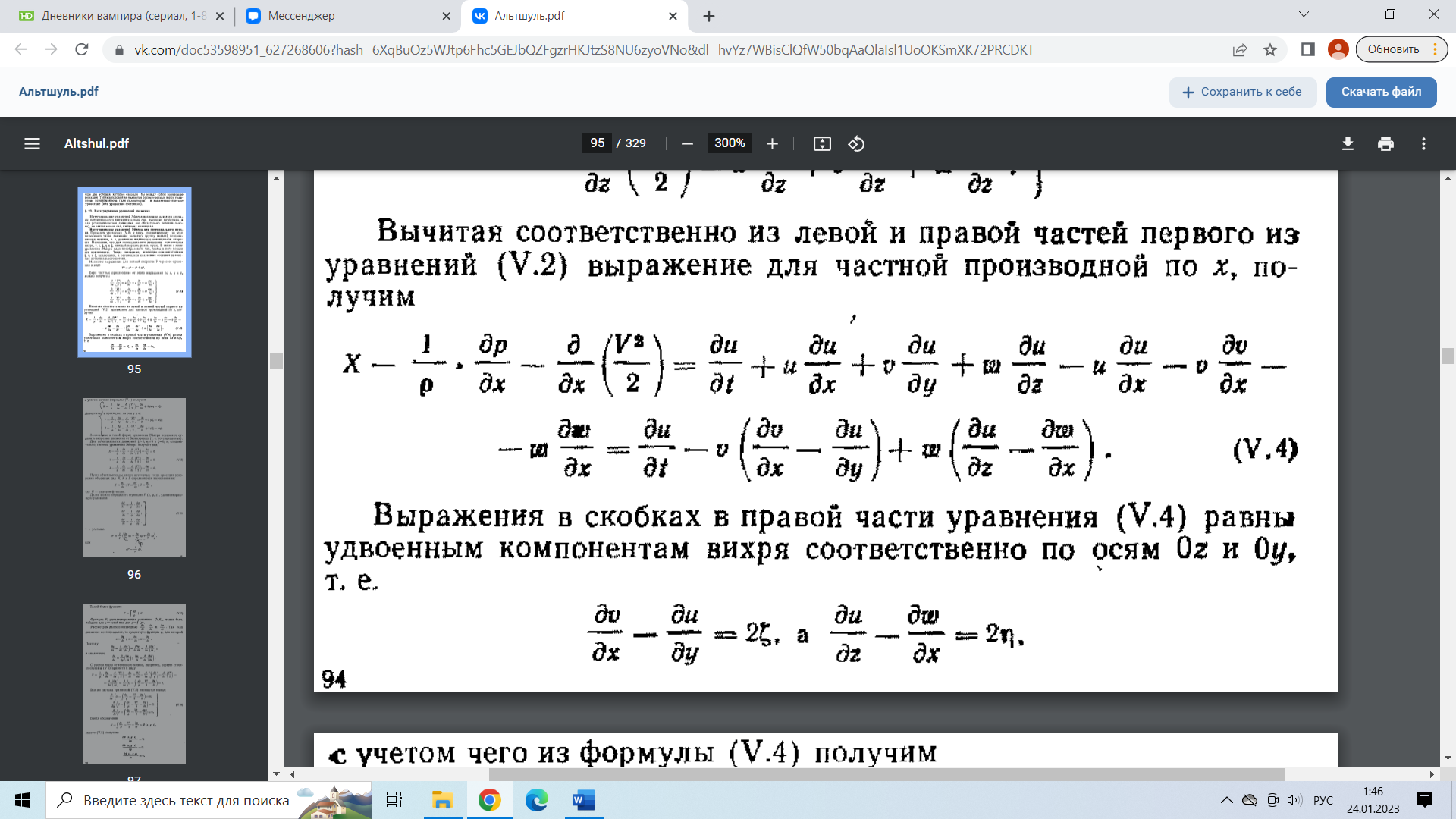 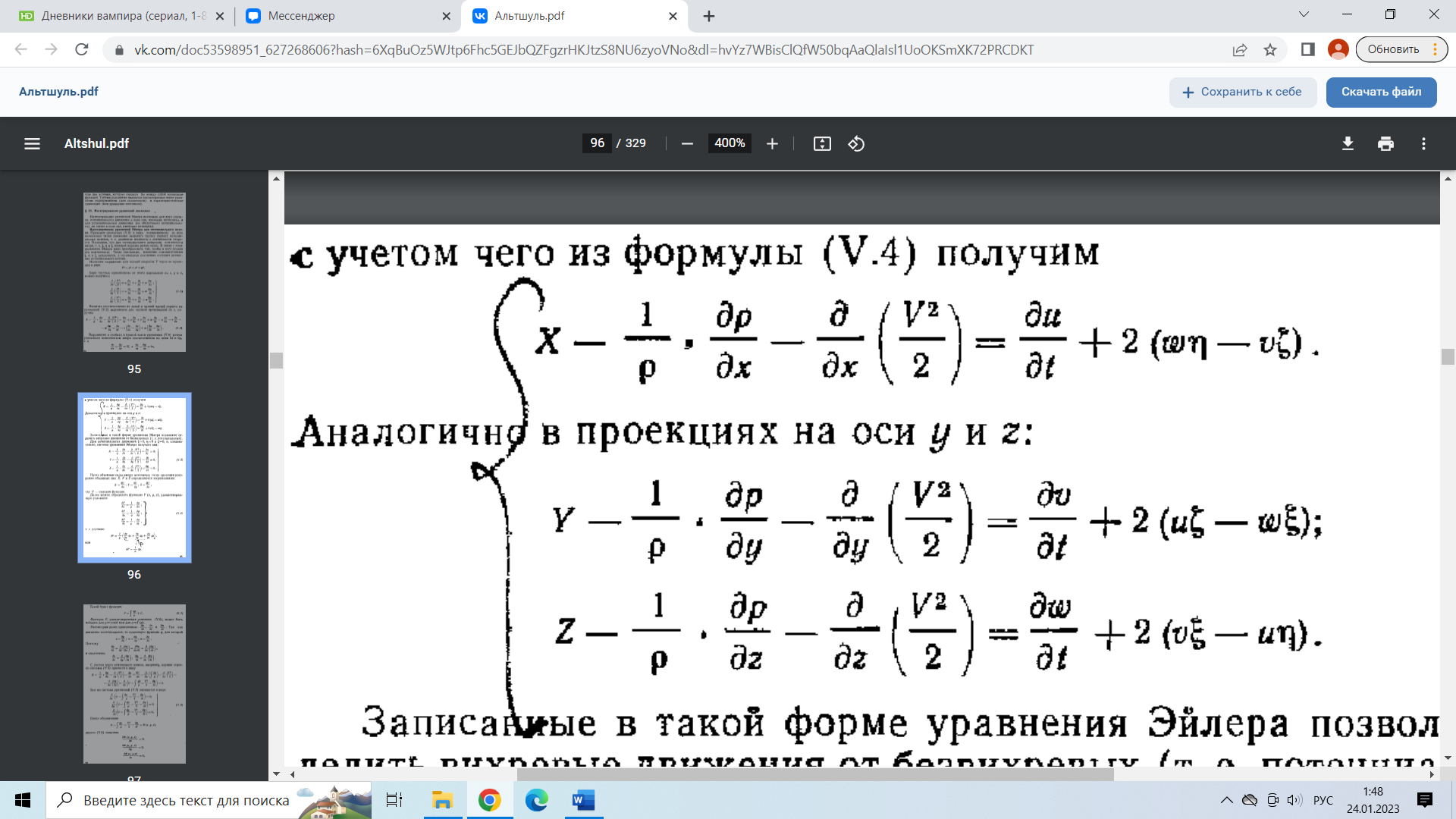 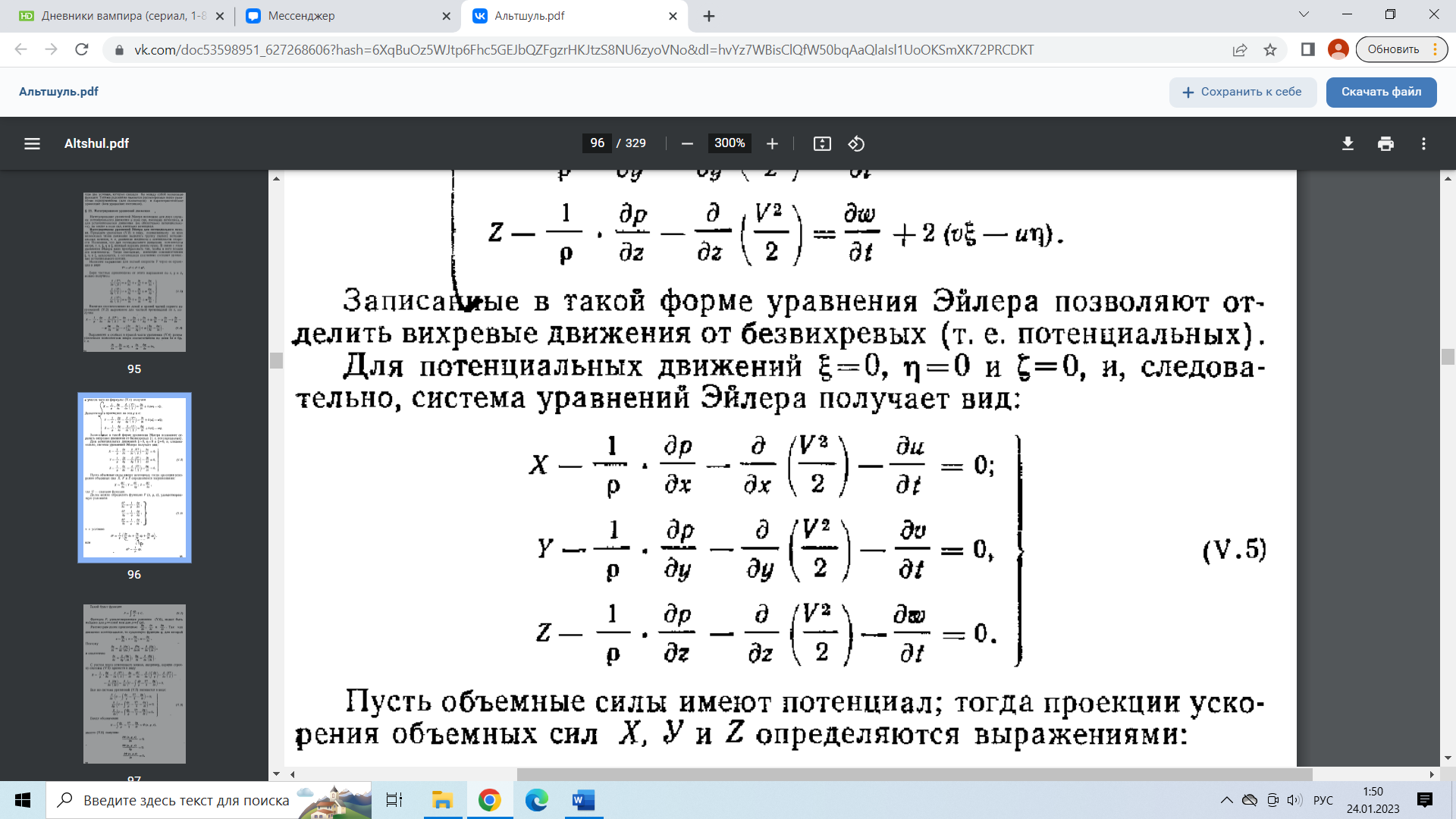 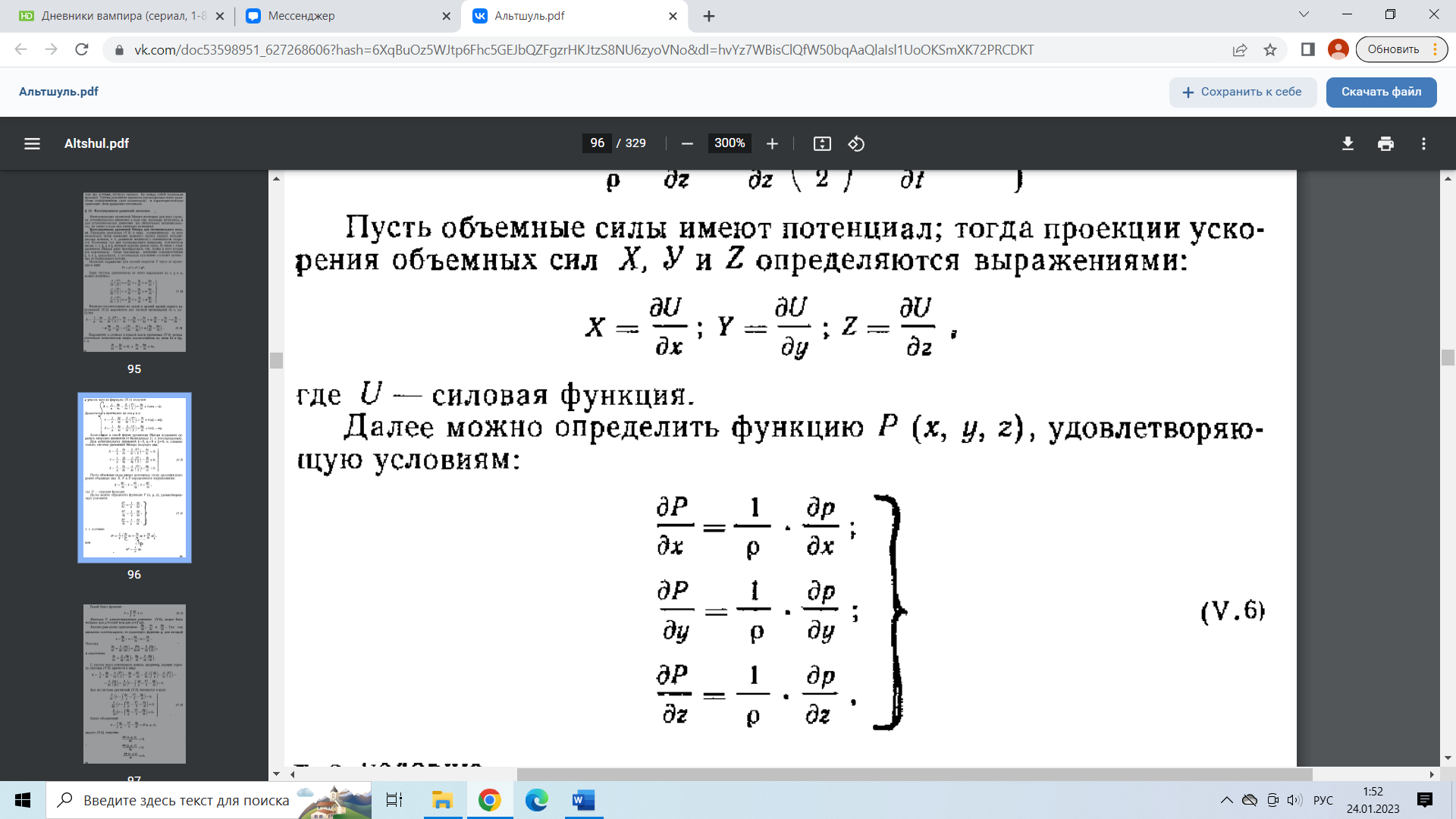 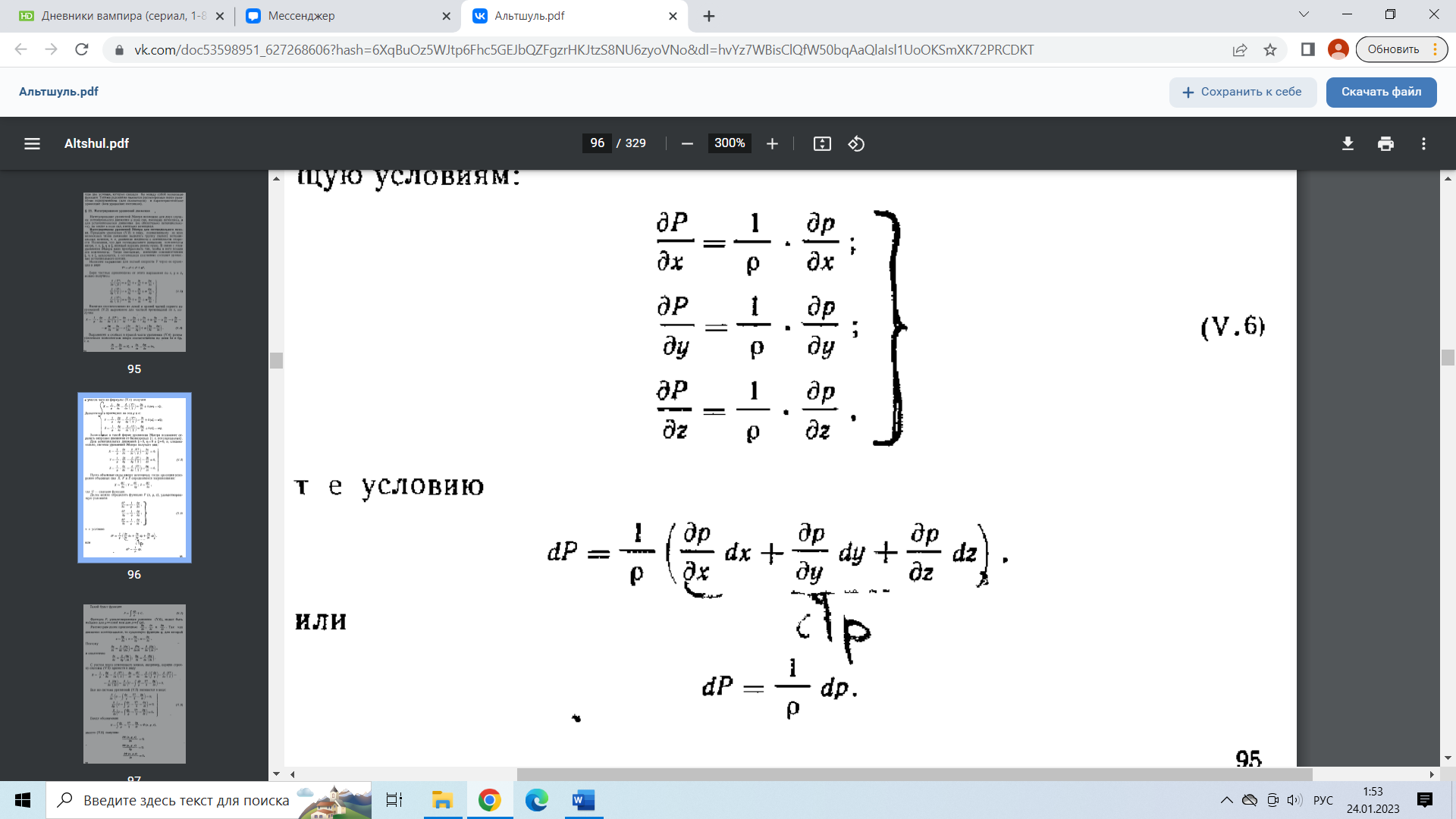 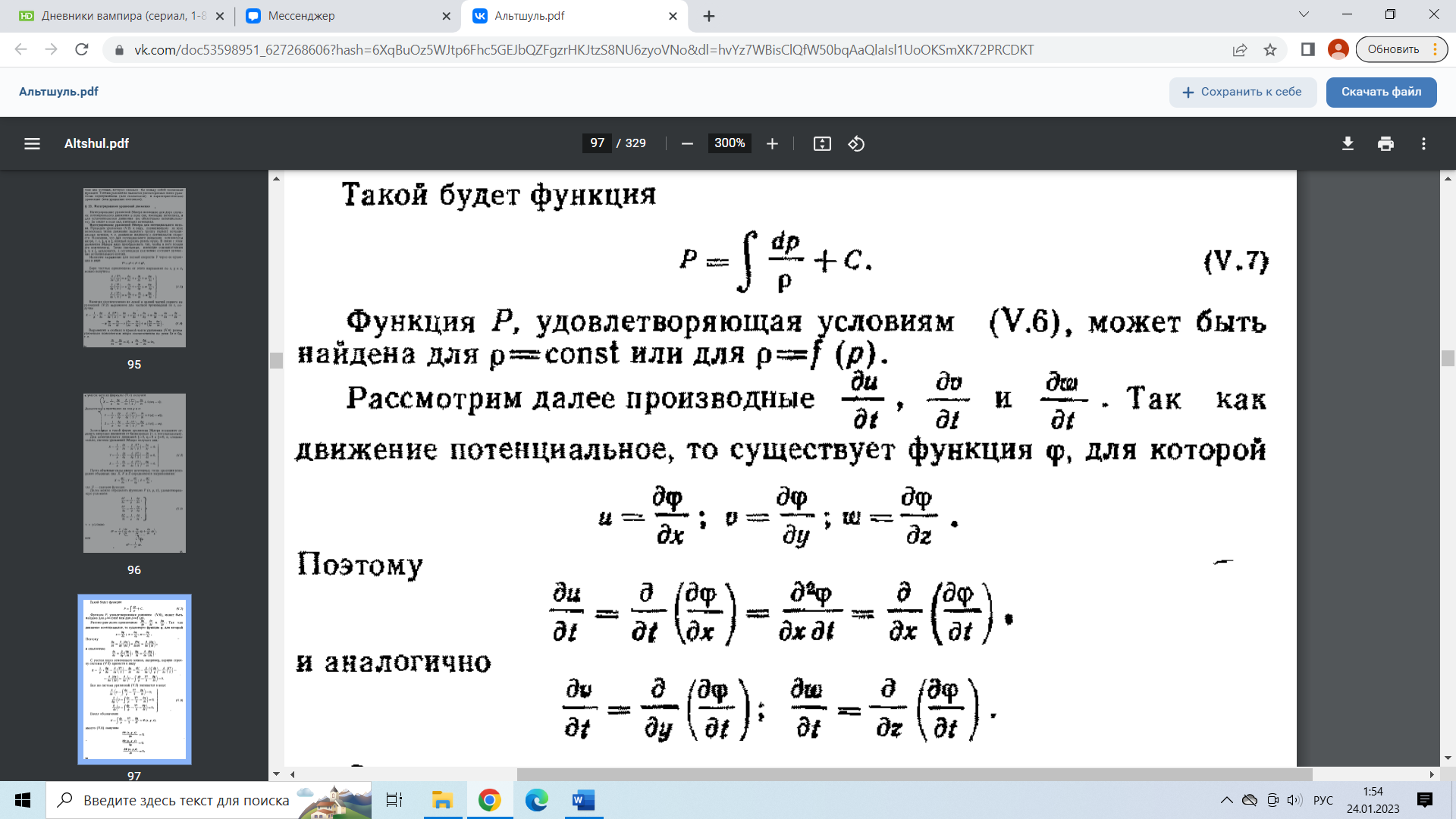 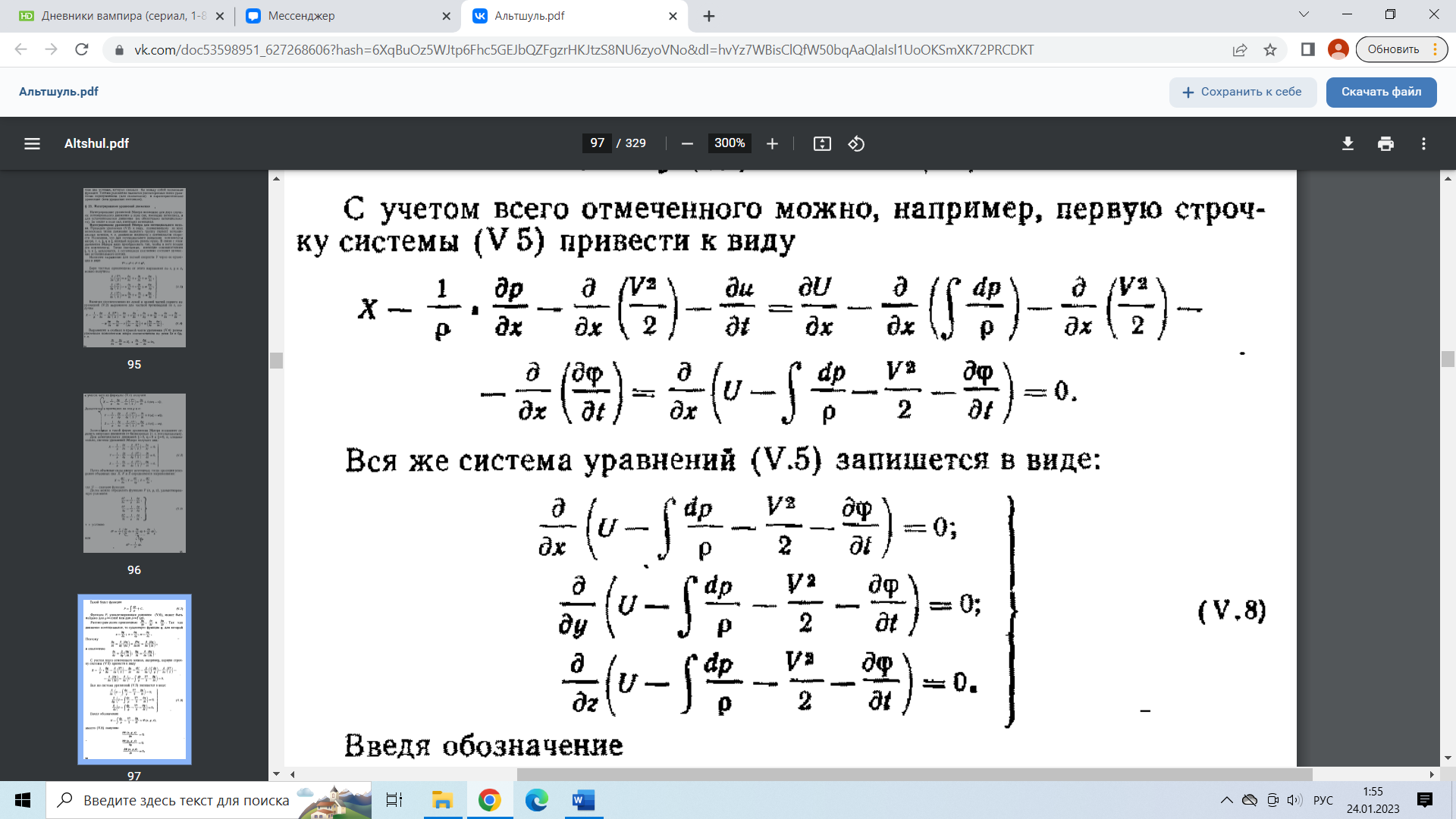 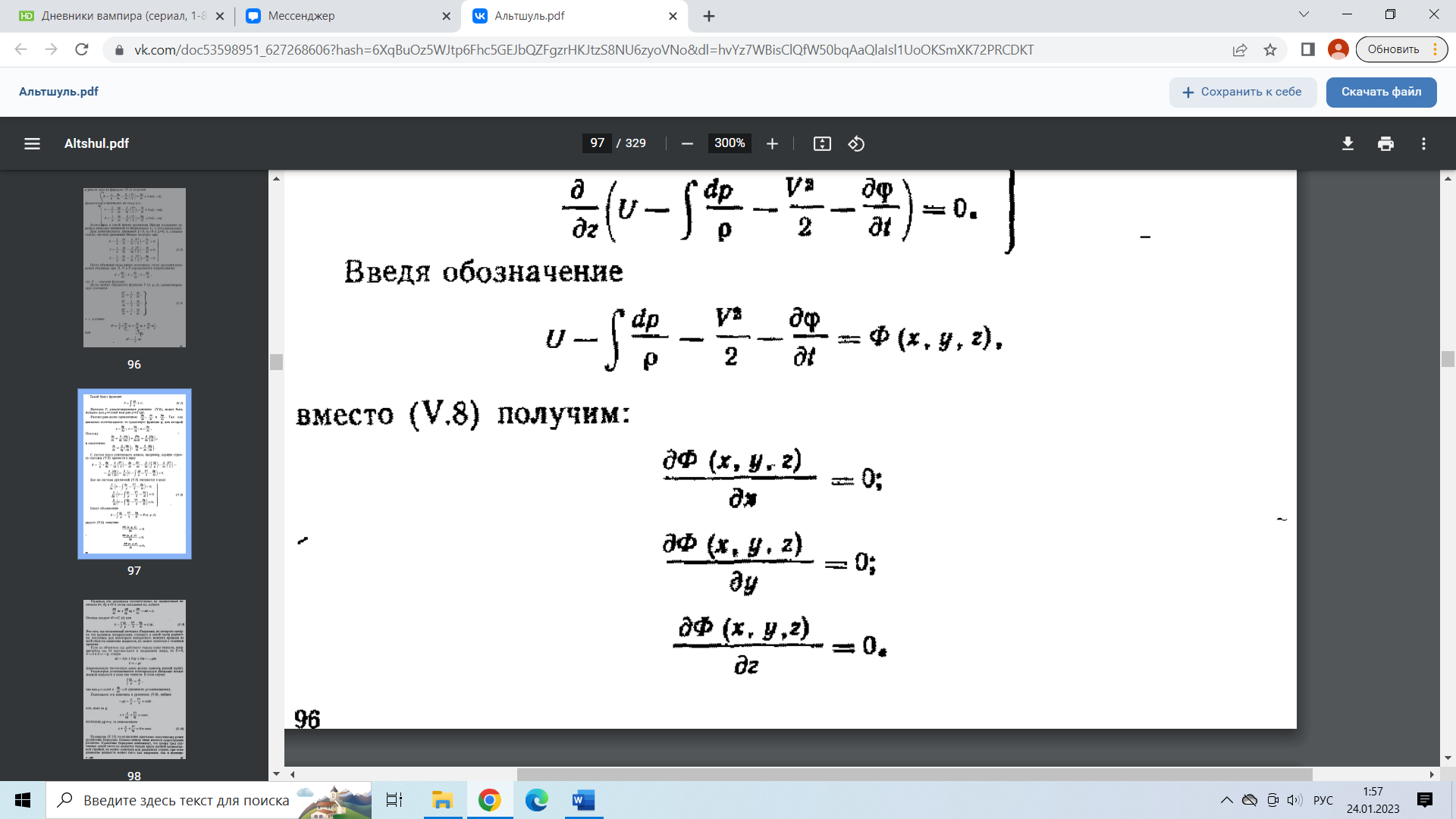 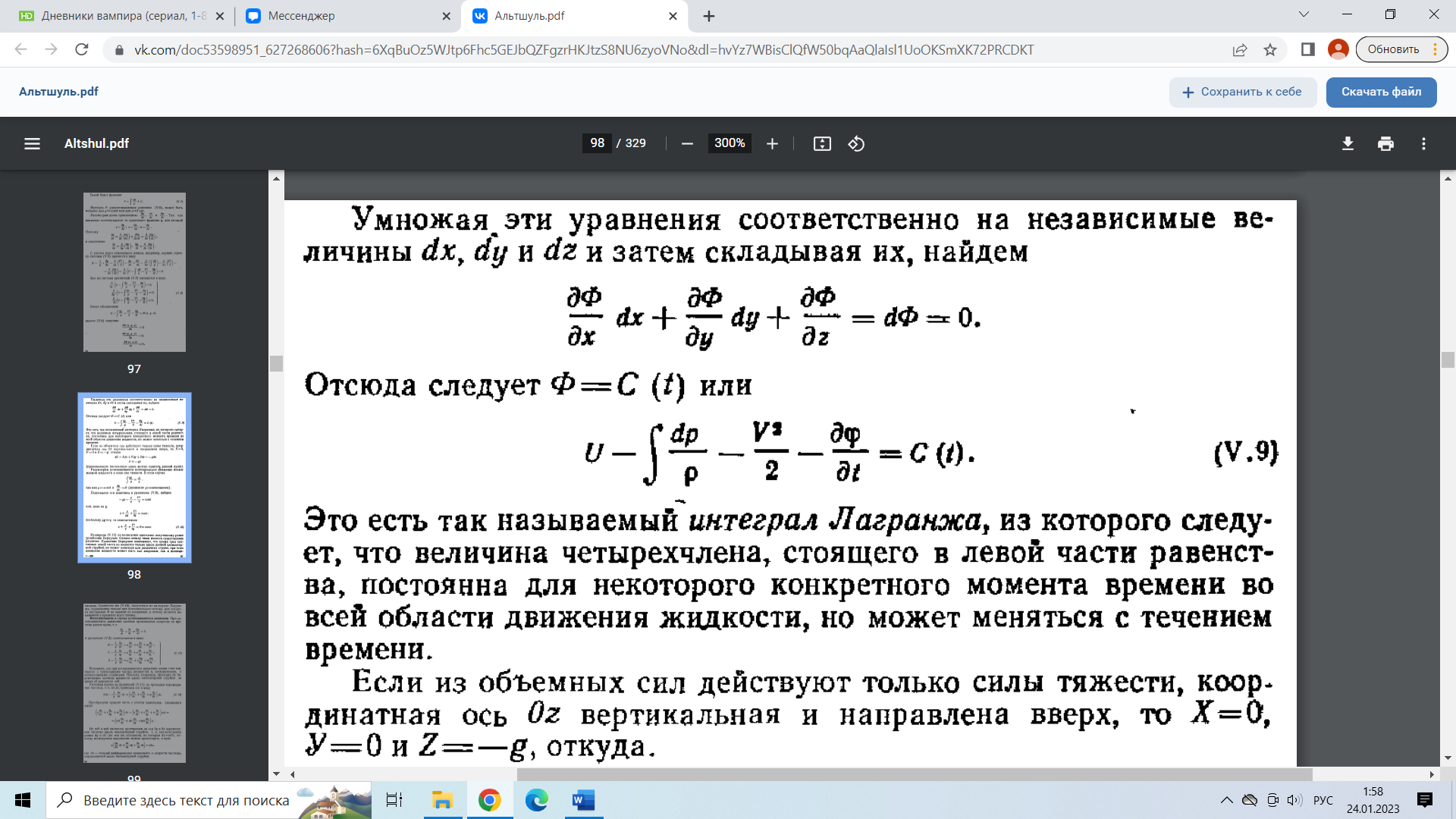 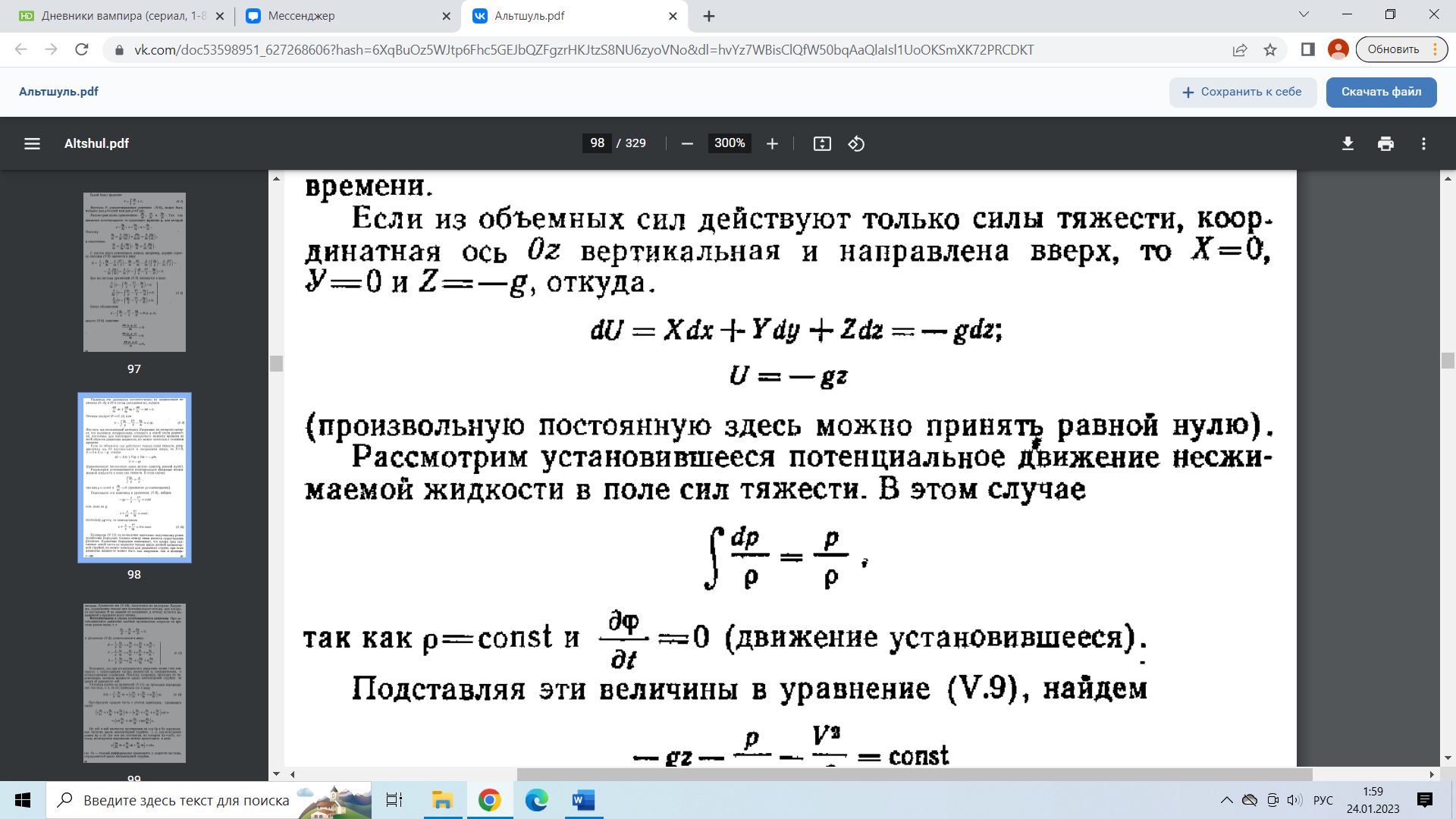 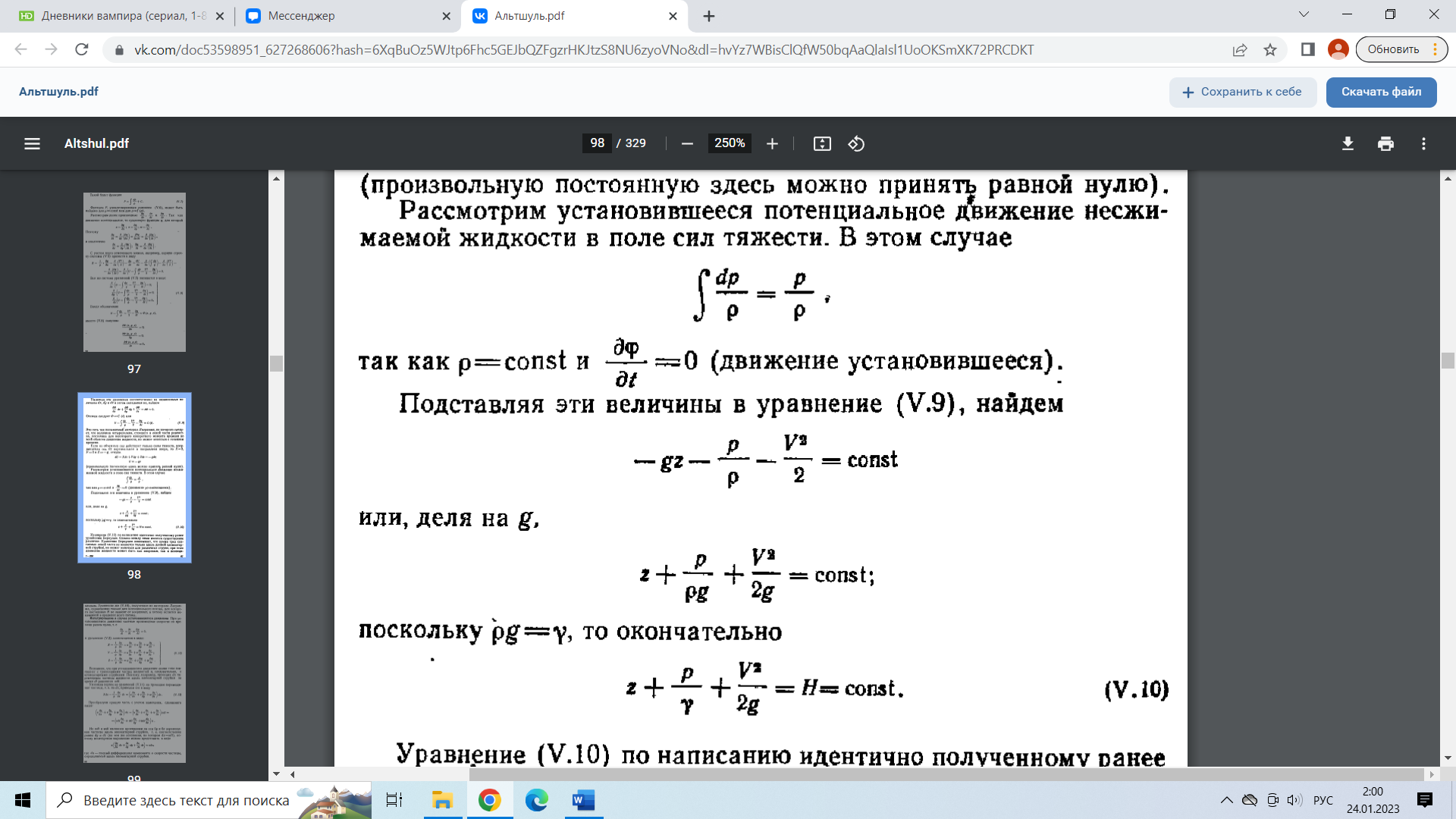 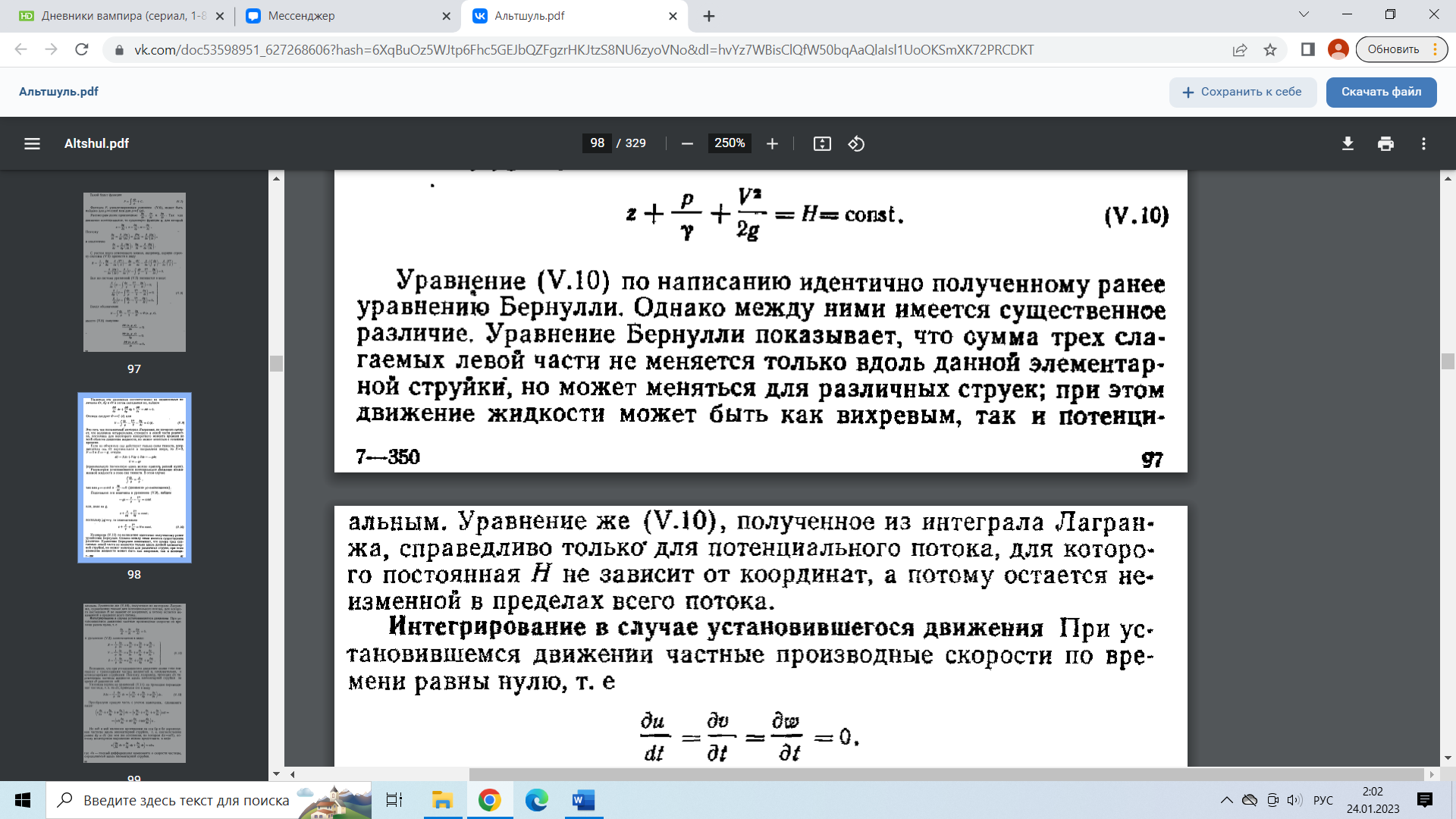  30.интегрирование в случае установившегося движения. Интеграл Эйлера-Бернулли.  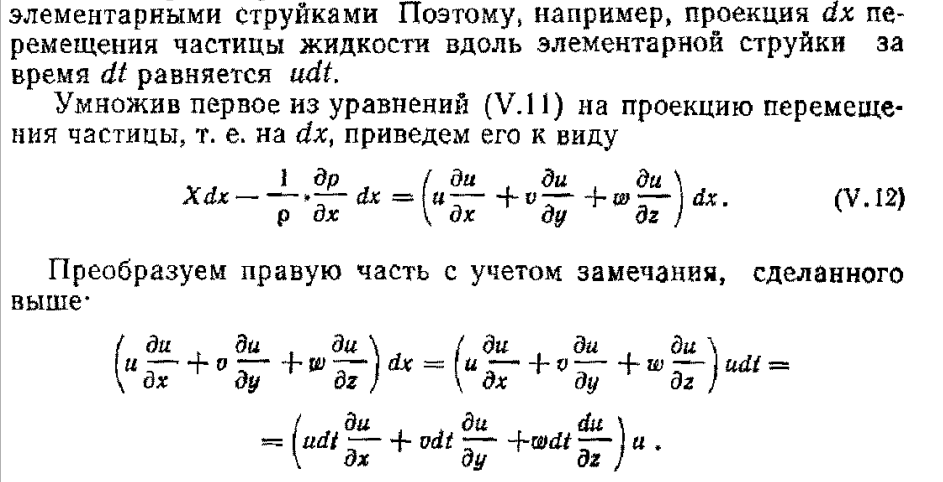  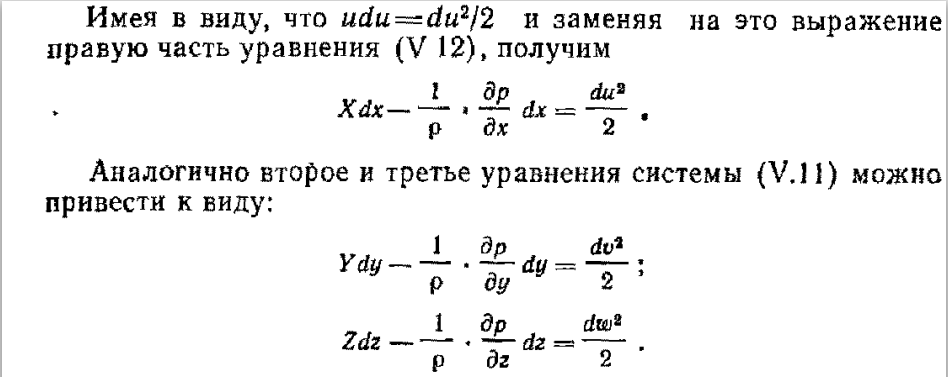  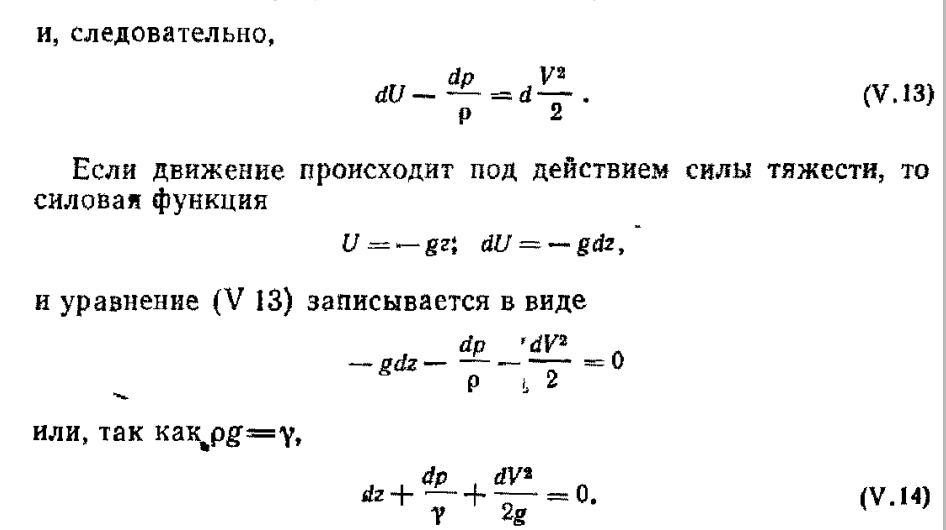  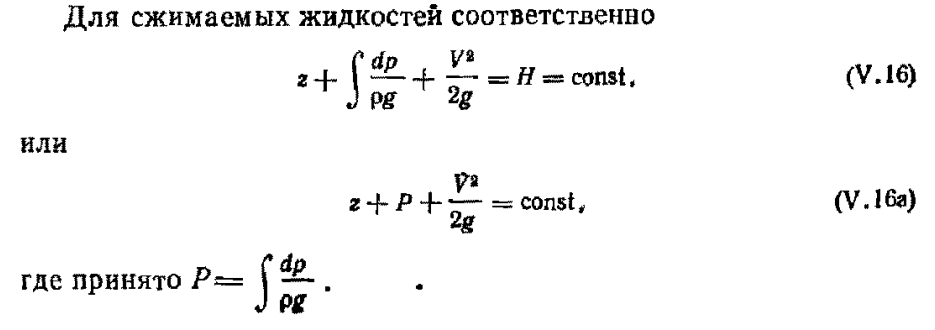 41. Определение компонент вихря и полного значения вихря при ламинарном движении. Существенно отметить, что ламинарное движение является вихревым. Чтобы убедиться в этом, найдем величину компонентов вихря 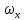 , , 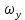 , , 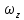 для этого движения. Для ламинарного потока в цилиндрической трубе: для этого движения. Для ламинарного потока в цилиндрической трубе: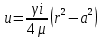 в соответствии с чем: 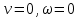 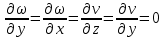 Но производные 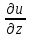 и и 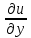 не равны нулю, а потому для компонентов вихря найдем: не равны нулю, а потому для компонентов вихря найдем: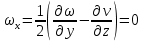 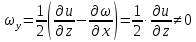 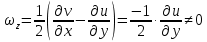 Следовательно, вихрь 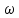 не равен нулю. не равен нулю.Представим выражение для скорости 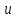 в функции координат в функции координат 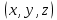 . .Так как 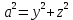 , то , то 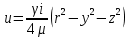 , откуда , откуда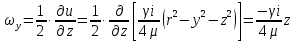 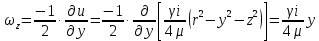 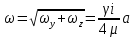 Максимальную скорость вращения имеют частицы у стенок трубы 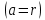 , ,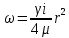 . Для частиц, расположенных на оси трубы, . Для частиц, расположенных на оси трубы, 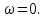 31. Уравнение движения вязкой жидкости (уравнение Навье - Стокса.) 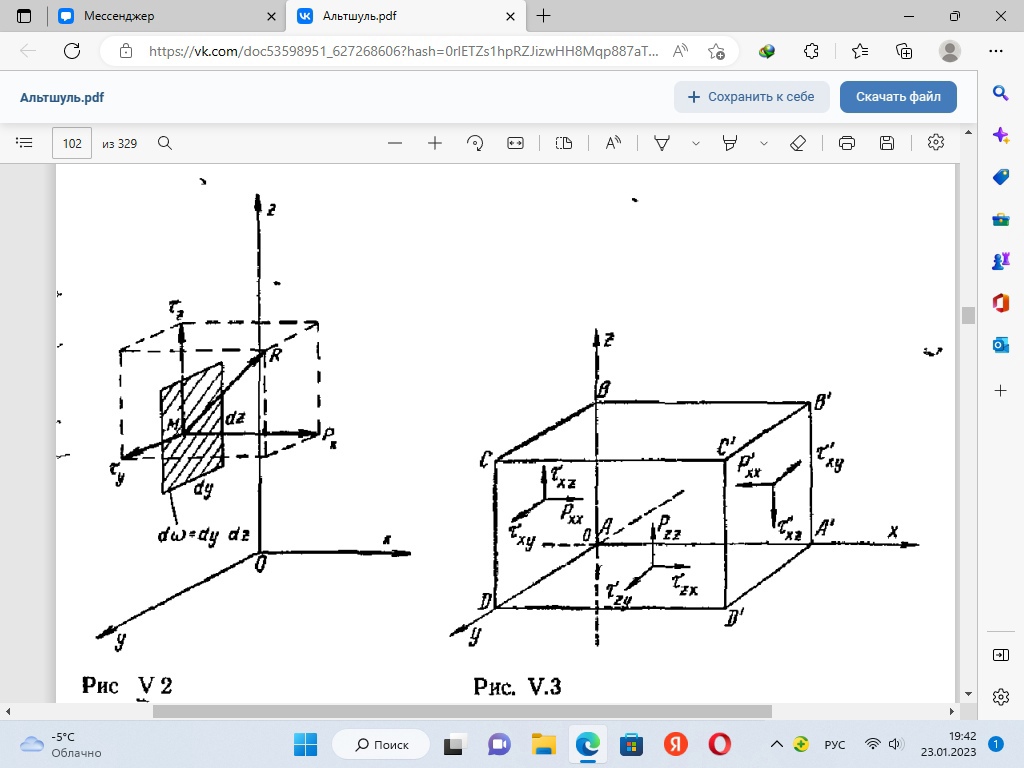 Дифференциальные уравнения движения вязкой жидкости могут быть составлены путем дополнения уравнений Эйлера теми слагаемыми, которые определяют собой силы сопротивления движению, обусловленные вязкостью жидкости. Дифференциальные уравнения движения вязкой жидкости могут быть составлены путем дополнения уравнений Эйлера теми слагаемыми, которые определяют собой силы сопротивления движению, обусловленные вязкостью жидкости. 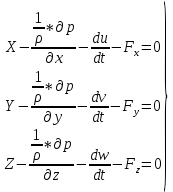 Где Fx, Fy, Fz - проекции сил вязкости на координатные оси, отнесенные к единице массы жидкости, т. е. записанные в виде ускорений Fx=F’x/ρ∆W (здесь F’x -проекция силы, действующей на массу ρ∆W, а Fx - проекция ускорения). Где Fx, Fy, Fz - проекции сил вязкости на координатные оси, отнесенные к единице массы жидкости, т. е. записанные в виде ускорений Fx=F’x/ρ∆W (здесь F’x -проекция силы, действующей на массу ρ∆W, а Fx - проекция ускорения).Под действием сил вязкости (сил сопротивления смещению од них частиц жидкости относительно других, смежных с ними) возникают как тангенциальные (касательные), так и нормальные напряжения (напряжения сжатия или растяжения). Найдем силы F’x, F’y, F’z; предполагая, что жидкость движется слоями без перемешивания движущейся массы. В общем случае направление движения не совпадает с направлением координатных осей, вследствие чего не совпадает с направлением этих осей и сила вязкости. Рассмотрим площадку d площадью dydz, лежащую в плоскости y0z. Пусть в некоторой точке М этой площади действует сила вязкости R, отнесенная к единице площади (как напряжение). Разложим эту силу по координатным осям на три составляющих. Тогда получим силу рх нормальную к данной площадке d, и две касательные силы: y, z .В соответствии с этим для всей площадки d получим три силы: нормальную Рx=pхdydz (параллельную оси Ох) и две касательные Ty=ydydz и Tz=zdydz, соответственно параллельные осям Oу и Ох. Понятно, что из этих трех сил только сила Px проектируется на ось Ох в натуральную величину, а силы Тx и Ту проектируются на ось Ох в нуль. Сказанное справедливо для любой площадки, выбранной в любой координатной плоскости. Теперь выделим элемент жидкости в форме параллелепипеда с ребрами, параллельными координатным осям, и определим сумму проекций сил вязкости, действующих только на те три грани параллелепипеда, которые образуют трехгранный угол с верши ной А. Отметим, что для каждой координатной оси мы получим проекции только трех сил (из девяти); остальные будут проектироваться в точку. Так, для оси Ох: Px=pxdydz; Tx,1=xdxdу и Тх,2=xdxdz. Для удобства дальнейших рассуждений введем двойную индексацию напряжений: например, для нормального напряжения рхх, для касательного напряжения ху и т. д.; здесь первый индекс указывает на то, что площадка, для которой определяется напряжение, расположена нормально к данной оси координат, а второй - направление действия напряжения. С учетом этого по лучим следующую запись проекции сил на ось Ох: Проекция нормальной силы на грань ABCD …. pxхdydz Касательной ABB’A’A …. yхdхdz AA’D’D …. zхdxdy Аналогичные выражения можем составить и для двух других координатных осей, в результате чего получим следующие выражения для проекций сил, действующих на грани трехгранного угла с вершиной А: Для оси Ох … pxхdydz; yхdхdz; zхdxdy Оу ... pyydxdz; хydydz; zydxdy Оz ... pzzdxdy; хzdydz; yzdxdz Переходя затем к проекциям сил, действующих на грани трехгранного угла с вершиной С', отметим, что напряжения на этих гранях будут отличаться от напряжений на гранях первого угла (с вершиной в точке А) на величину соответствующих частных дифференциалов этих напряжений. Следовательно: Для оси Ох … p’xхdydz; 'yхdхdz; 'zхdxdy Оу ... p'yydxdz; 'хydydz; 'zydxdy Оz ... p'zzdxdy; 'хzdydz; 'yzdxdz где для оси Ох: p'xх 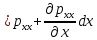 'yх 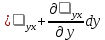 'zх 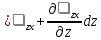 Аналогичные выражения можно получить и для двух других осей. Составим теперь выражение для силы F’x, представляющей собой, как сказано выше, сумму проекций на ось Ох всех сил вязкости, действующей на массу жидкости в объеме выделенного параллелепипеда. Полагая, что направление сил, действующих на грани угла с вершиной С, противоположно направлению сил, действующих на грани трехгранного угла с вершиной А, получим 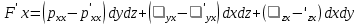 Но: pxx-p'xх 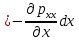 yх -'yх 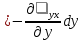 zх -'zх 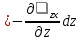 в силу чего, делая соответствующую подстановку, найдем 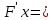 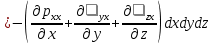 Сила 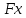 , входящая в уравнение Эйлера, как указано выше, , входящая в уравнение Эйлера, как указано выше,представляет собой проекцию силы вязкости, отнесенную к единице массы жидкости, т. е. Fx=F’x/ρ∆W, где в данном случае ∆W=dxdydz, а поэтому для силы Fx, получим следующее выражение: 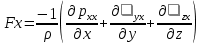 Здесь 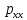 - нормальные, а - нормальные, а 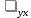 и и 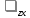 - касательные напряжения. - касательные напряжения.Касательные напряжения 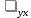 в пределах грани dxdz остаются в пределах грани dxdz остаютсяодинаковыми для всех точек этой площадки, т. е. не зависят от координат х и z и изменяются только при перемещении этой площадки вдоль оси Оу, т. е. зависят от координаты у. Другими словами, 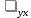 - это касательные напряжения, зависящие только от - это касательные напряжения, зависящие только отградиента скорости 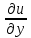 . Поэтому в соответствии с законом Ньютона yx=ϻ . Поэтому в соответствии с законом Ньютона yx=ϻ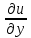 и по аналогии zx=ϻ и по аналогии zx=ϻ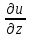 , ,Откуда 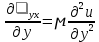 и и 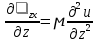 . .Рассмотрим производную 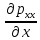 . Здесь . Здесь 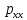 представляет представляетсобой нормальиое к площади dydz напряжение, обусловленное влияннем вязкости (сжатия - в условиях торможения и растяжения - в условиях ускоренного движения) в зависимости от изменения скорости вдоль оси Ох, т. е. в зависимости от градиента скорости 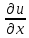 . Поэтому можно допустить, что напряжение . Поэтому можно допустить, что напряжение 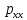 может также определяться по закону Ньютона: pxx=ϻ может также определяться по закону Ньютона: pxx=ϻ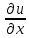 ; а ; атогда 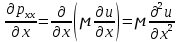 . .Делах соответствующие подстановки в уравнение, получим 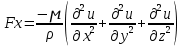 или, так как ϻ/ρ=ν (кинематической вязкости), или, так как ϻ/ρ=ν (кинематической вязкости),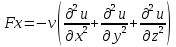 Аналогично получим: Аналогично получим: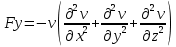 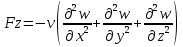 Вводя теперь полученные выражения сил Fx, Fy, Fz в систему уравнений, после некоторой перестановки слагаемых в окончательной форме запишем дифференциальные уравнения движения вязкой жидкости: 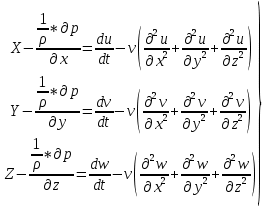 Эти уравнения именуются уравнениями Навье - Стокса. Эти уравнения именуются уравнениями Навье - Стокса. |
