курсач. Курсовая работа По дисциплине Теплотехнический расчет транспортно технологических систем
 Скачать 79.86 Kb. Скачать 79.86 Kb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Федеральное государственное бюджетное образовательное учреждение высшего образования «ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ (ФГБОУ ВО ИрГУПС)» Факультет транспортных систем Кафедра «Вагоны и вагонное хозяйство» Курсовая работа По дисциплине: «Теплотехнический расчет транспортно – технологических систем» Выполнил Проверил студент гр. ЭТТм.1-22-1 к.т.н., доцент Дроняк Д. П. Матвиенко А. С. Иркутск 2022 Задание 1В секционном теплообменном аппарате типа «труба в трубе» вода с расходом 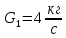 , движущаяся по внутренней трубе, охлаждается до , движущаяся по внутренней трубе, охлаждается до 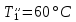 . Холодная вода с расходом . Холодная вода с расходом 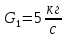 поступает в аппарат с температурой поступает в аппарат с температурой 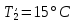 . Конструктивные параметры теплообменника: внутренний диаметр большой трубы . Конструктивные параметры теплообменника: внутренний диаметр большой трубы 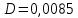 м, внутренний диаметр малой трубы м, внутренний диаметр малой трубы 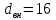 мм, наружный мм, наружный 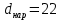 мм, длина каждой секции не более мм, длина каждой секции не более 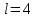 м, количество трубок в каждой секции (внутри большой трубы) м, количество трубок в каждой секции (внутри большой трубы) 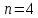 . Трубы выполнены из нержавеющей стали. Температура горячего теплоносителя на выходе в теплообменный аппарат принять их интервала . Трубы выполнены из нержавеющей стали. Температура горячего теплоносителя на выходе в теплообменный аппарат принять их интервала 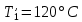 . Определить число параллельно и последовательно соединенных секций . Определить число параллельно и последовательно соединенных секций 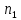 и и 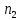 , тепловую мощность аппарата Q, скорости движения теплоносителей , тепловую мощность аппарата Q, скорости движения теплоносителей 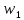 и и 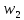 , и температуру холодного теплоносителя на выходе из аппарата , и температуру холодного теплоносителя на выходе из аппарата 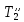 . Схема движения теплоносителей – противоток. . Схема движения теплоносителей – противоток.Решение. Тип расчёта – тепловой конструктивный. При выполнении теплового конструктивного расчета определяют поверхность теплообмена, необходимую для нагрева холодного теплоносителя или охлаждения горячего теплоносителя до заданной температуры. Последовательность теплового конструктивного расчета следующая: 1. Из уравнения теплового баланса находим тепловую мощность аппарата Q и температуру холодного теплоносителя на выходе из теплообменника 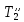 . .Для однофазных теплоносителей уравнение теплового баланса примет вид: 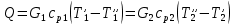 Поскольку температуры горячего теплоносителя заданы по условию, то из левой части уравнения теплового баланса рассчитываем тепловую мощность теплообменника Q. Для этого по табл. 1.65 [1] при средней температуре горячего теплоносителя 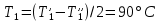 находим удельную теплоемкость воды находим удельную теплоемкость воды 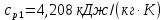 . .Тогда тепловая мощность аппарата равна: 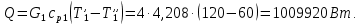 Зная Q, из правой части уравнения теплового баланса находим температуру холодного теплоносителя на выходе из теплообменного аппарата: 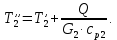 Удельная теплоемкость 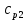 зависит от искомой температуры зависит от искомой температуры 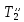 , поэтому расчет ведем методом последовательных приближений. , поэтому расчет ведем методом последовательных приближений. В первом приближении примем 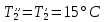 . По табл. 1.74 [1] при средней температуре холодного теплоносителя . По табл. 1.74 [1] при средней температуре холодного теплоносителя 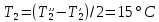 находим находим 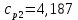 кДж/(кг·К). кДж/(кг·К). Рассчитываем температуру холодного теплоносителя на выходе во втором приближении: 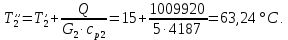 Расхождение между принятым и полученным значениями температуры 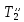 составляет составляет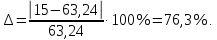 Погрешность итерационного процесса определения температуры 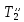 больше 5 %, поэтому расчет повторяем. При этом удельную теплоемкость воды находим по табл. 1.74 [1] для нового значения больше 5 %, поэтому расчет повторяем. При этом удельную теплоемкость воды находим по табл. 1.74 [1] для нового значения 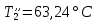 . При средней температуре холодного теплоносителя . При средней температуре холодного теплоносителя 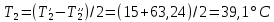 находим находим 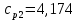 кДж/(кг·К). кДж/(кг·К). Рассчитываем температуру холодного теплоносителя на выходе в третьем приближении: 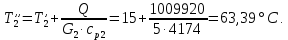 Расхождение между принятым и полученным значениями температуры 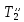 составляет составляет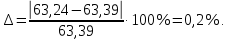 Расхождение между температурами второго и третьего приближения меньше 5 %, поэтому расчет заканчиваем. Для дальнейших расчетов принимаем температуру холодного теплоносителя на выходе равной 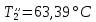 2. Из уравнения неразрывности (1.12) определяем скорость движения горячего и холодного теплоносителей. При этом для секционного теплообменника типа «труба в трубе» предварительно необходимо найти количество параллельно 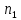 соединенных секций. Алгоритм определения соединенных секций. Алгоритм определения 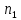 приведен в разделе 3.3 учебного пособия. приведен в разделе 3.3 учебного пособия. – Из уравнения неразрывности находим скорости движения теплоносителей без распараллеливания потоков теплоносителей, т.е. при 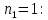  В данном случае воздух движется в межтрубном пространстве, поэтому площадь поперечного сечения для прохода горячего теплоносителя равна   Холодный теплоноситель вода движется в трубках, поэтому площадь поперечного сечения для прохода холодного теплоносителя находим по формуле  Плотность горячей воды находим при средней температуре 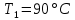 по табл. 1.74 [1] по табл. 1.74 [1] 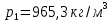 . Плотность холодной воды находим при средней температуре . Плотность холодной воды находим при средней температуре 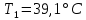 по табл. 1.74 [1] по табл. 1.74 [1] 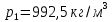 . .Рассчитываем скорости движения теплоносителей при 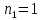 : :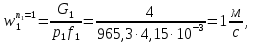 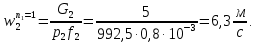 – Сравниваем значения скоростей 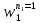 и и 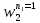 с рекомендуемым интервалом изменения скоростей: с рекомендуемым интервалом изменения скоростей: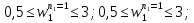 Скорость горячего теплоносителя попадает в требуемый диапазон значений, а скорость холодного теплоносителя превышает максимально допустимую 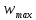 , поэтому необходимо распараллеливание потока горячего теплоносителя. , поэтому необходимо распараллеливание потока горячего теплоносителя.– Выбираем число параллельных секций 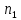 таким образом, чтобы скорость воды таким образом, чтобы скорость воды 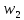 находилась в рекомендуемом интервале значений. Для этого примем скорость холодного теплоносителя (воды), например, зад находилась в рекомендуемом интервале значений. Для этого примем скорость холодного теплоносителя (воды), например, зад 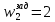 и определим число параллельных секций для движения холодного теплоносителя и определим число параллельных секций для движения холодного теплоносителя 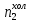 по формуле: по формуле: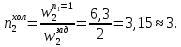 Уточняем 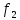 и и 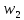 при при 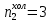 : :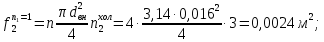 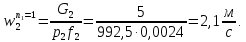 3. Строим график изменения температур теплоносителей вдоль поверхности нагрева Т=f(F) и рассчитываем среднюю разность температур теплоносителей 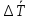 . . Схема движения теплоносителей – противоток. Так как 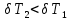 , и соответственно , и соответственно 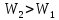 , то выпуклость кривых изменения температуры теплоносителей направлена в сторону холодного теплоносителя – вниз. , то выпуклость кривых изменения температуры теплоносителей направлена в сторону холодного теплоносителя – вниз.Из графика Т=f(F) определяем максимальную и минимальную разности температур теплоносителей: 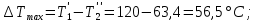 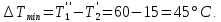 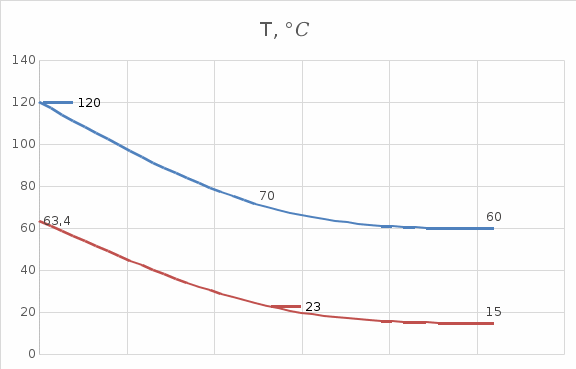 Рис. 1. Изменение температуры теплоносителей вдоль поверхности нагрева Отношение 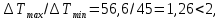 поэтому среднюю разность температур рассчитываем по формуле: поэтому среднюю разность температур рассчитываем по формуле: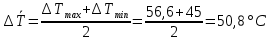 4. Рассчитываем коэффициенты теплоотдачи 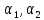 и коэффициент теплопередачи k. и коэффициент теплопередачи k.Основная сложность определения коэффициентов теплоотдачи 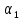 и и 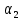 заключается в том, что в критериальные формулы входят величины, зависящие от температур наружной и внутренней стенок заключается в том, что в критериальные формулы входят величины, зависящие от температур наружной и внутренней стенок 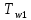 и и 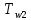 , поэтому расчёт ведут методом последовательных приближений по одному из алгоритмов, описанных в разделе 1.5. Выполним расчет по первому алгоритму. , поэтому расчёт ведут методом последовательных приближений по одному из алгоритмов, описанных в разделе 1.5. Выполним расчет по первому алгоритму. – Задаем неизвестные температуры стенок 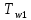 и и 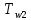 в первом приближении: в первом приближении: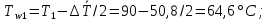 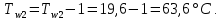 – По табл. 1.11 [1] при средней температуре стенки 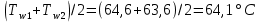 находим коэффициент теплопроводности хромистой нержавеющей стали марки 1Х13 (Ж1) находим коэффициент теплопроводности хромистой нержавеющей стали марки 1Х13 (Ж1) 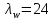 Вт/(мК). Вт/(мК). – По критериальным уравнениям определяем коэффициенты теплоотдачи со стороны горячего и холодного теплоносителей 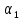 и и 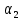 . .Находим коэффициент теплоотдачи при вынужденном движении воздуха в межтрубном пространстве 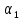 . . При движении теплоносителя в каналах сложной формы в качестве определяющего размера принимают эквивалентный диаметр 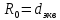 , который для межтрубного пространства теплообменника «труба в трубе» с числом трубок n рассчитывается по формуле , который для межтрубного пространства теплообменника «труба в трубе» с числом трубок n рассчитывается по формуле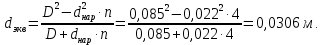 По табл. 1.74 [1] при определяющей температуре 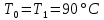 находим физические свойства воды: находим физические свойства воды: 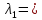 68 Вт/(мК); 68 Вт/(мК); 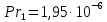 Пас; Пас; 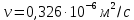 . При температуре стенки . При температуре стенки 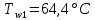 находим находим 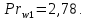 Рассчитываем критерий Рейнольдса и определяем режим течения: 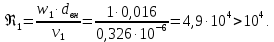 Число Рейнольдса больше 10000, поэтому режим течения воздуха турбулентный. По критериальной формуле (1.41) для турбулентного режима течения получим: 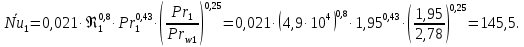 Находим коэффициент теплоотдачи 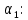 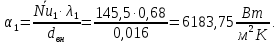 Находим коэффициент теплоотдачи 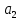 . .По табл. 1.74 [1] при определяющей температуре 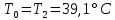 находим физические свойства воды: находим физические свойства воды: 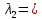 63,35 Вт/(мК); 63,35 Вт/(мК); 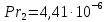 Пас; Пас; 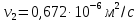 . При температуре стенки . При температуре стенки 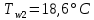 находим находим 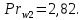 Определяющий размер – внутренний диаметр трубок 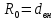 . . Рассчитываем критерий Рейнольдса и определяем режим течения: 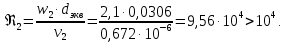 Число Рейнольдса больше 10000, поэтому режим течения воздуха турбулентный. По критериальной формуле (1.41) для турбулентного режима течения получим: 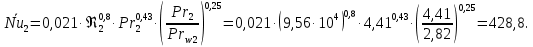 Находим коэффициент теплоотдачи 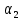 : :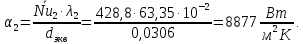 – Определяем коэффициент теплопередачи k. Отношение наружного диаметра стенки трубы к внутреннему диаметру меньше двух ( 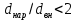 ), поэтому коэффициент теплопередачи рассчитываем по формуле для плоской стенки. При этом термическим сопротивлением загрязнений пренебрегаем ( ), поэтому коэффициент теплопередачи рассчитываем по формуле для плоской стенки. При этом термическим сопротивлением загрязнений пренебрегаем (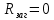 ). ).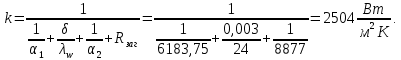 – Уточняем температуры стенок 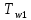 и и 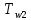 . Для этого рассчитаем плотность теплового потока через стенку между средними температурами . Для этого рассчитаем плотность теплового потока через стенку между средними температурами 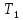 и и 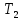 теплоносителей теплоносителей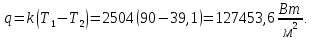 Температуры стенок найдем по формулам 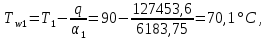 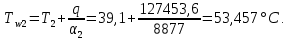 Расхождение между принятым и полученным значениями температуры составляет: 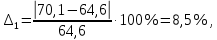 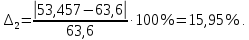 Так как расхождение больше 5 %, то расчет проводим аналогично пункту 4 для новых значений 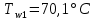 и и 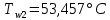 . Заметим, что в формулах для расчета . Заметим, что в формулах для расчета 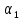 и и 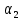 изменятся только значение критериев Прандтля изменятся только значение критериев Прандтля 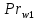 и и 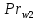 . . Из табл. 1.11 [1] найдем коэффициент теплопроводности хромистой нержавеющей стали марки 1Х13 (Ж1) 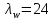 Вт/(мК) при средней температуре стенки Вт/(мК) при средней температуре стенки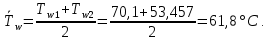 Рассчитываем 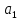 и и 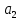 . . По табл. 1.65 [1] при температуре стенки 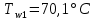 находим находим 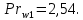 По табл. 1.74 [1] при температуре стенки 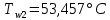 находим находим 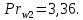 Рассчитываем коэффициент теплоотдачи 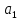 : :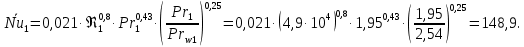 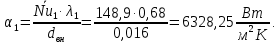 Рассчитываем коэффициент теплоотдачи 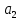 : :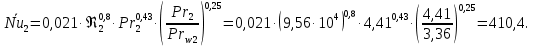 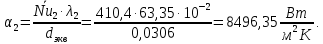 Рассчитываем коэффициент теплоотдачи k: 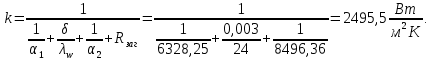 Уточняем температуры стенок 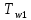 и и 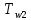 . .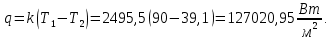 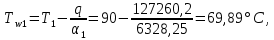 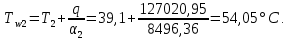 Расхождение между принятым и полученным значениями температуры составляет: 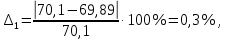 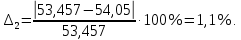 Так как расхождение между рассчитанным вновь и предыдущим значениями температур стенок меньше 5 %, то расчет заканчиваем. Для дальнейших расчетов принимаем коэффициент теплопередачи равным 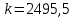 Вт/(м2·К). Вт/(м2·К). 5. Находим площадь поверхности теплообмена F из уравнения теплопередачи (1.19):  6. Определяем количество последовательно соединенных секций  по формуле (3.22). При условии по формуле (3.22). При условии  в качестве расчетного принимаем внутренний диаметр в качестве расчетного принимаем внутренний диаметр  . . По условию задачи l 4 м, длину каждой секции принимаем равной l = 2м. 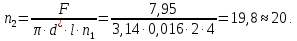 Уточняем длину трубок по формуле 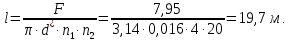 Использованные источники 1. Бухмиров, В.В. Справочные материалы для решения задач по курсу «Тепломассообмен»: учеб. пособие / В.В. Бухмиров, Д.В. Ракутина, Ю.С. Солнышкова; ГОУ ВПО «Ивановский государственный энергетический университет имени В.И. Ленина». – Иваново: ИГЭУ, 2009. – 102 с. |
