КУРСОВАЯ. Курсовая работа по курсу Специальные разделы математического анализа и геометрии тема Поверхностные интегралы первого типа Выполнил студент m 22 группы 2 курса очной формы обучения
 Скачать 175.37 Kb. Скачать 175.37 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ Государственное образовательное учреждение высшего образования Московской области МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОБЛАСТНОЙ УНИВЕРСИТЕТ (МГОУ) Кафедра математического анализа и геометрии КУРСОВАЯ РАБОТА по курсу «Специальные разделы математического анализа и геометрии» тема: Поверхностные интегралы первого типа Выполнил студент: M-22 группы 2 курса очной формы обучения физико-математического факультета Мирошкина Маргарита Станиславовна (ФИО) Научный руководитель: _________________________________ (уч. степень, звание,ФИО) Дата защиты: «___» __________ 2019 г. Оценка:___________________________ __________________________________ (подпись научного руководителя) Регистрационный номер _________ Дата регистрации:_______________ Мытищи 2019 Содержание §1. Введение………………………………………………………………………3 §2. Поверхностный интеграл 1-ого рода……………………………………..5 §3. Применение теории на практике………………………………………….6 §4. Список литературы………………………………………………...………17 §1. Введение Что такое поверхностный интеграл? Поскольку речь идет о понятии «интегрирование», проще всего описать его, как бесконечно большую сумму бесконечно малых величин по поверхности. Для примера можно представить озеро, дно которого далеко не является ровным и гладким. Где-то его неровности делают озеро более мелким, где-то более глубоким. И если вдруг будет поставлена задача вычислить водоизмещение озера, нужно будет учитывать и мель, и глубокие места, и другие неровности дна, чтобы правильно определить объем, занимаемый водой. В таком случае, чтобы вычислить поверхность дна озера, на помощь и приходит поверхностный интеграл первого рода. И, воспользовавшись, введением системы координат можно получить математическое представление задачи 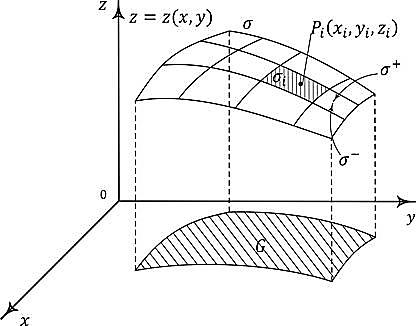 Рис.1 Представление поверхности озера в системе координат позволит вычислить ее с помощью поверхностного интеграла первого рода, чтобы в дальнейшем учитывать полученный результат при определении водоизмещения озера. И этот утрированный пример не так далёк от сути – поверхностные интегралы получили широчайшее распространение не только в математике, но и в физике, где часто возникает надобность подсчитать ту или иную физическую величину по поверхности. Поверхности тоже бывают неоднородны. В задачах на практике встречаются «обычные» и «кусочно-гладкие», то есть образованные из «кусков» сфер, цилиндров и других видов поверхностей. Поверхность обычно обозначают буквой σ, Ω или S. Поверхностный интеграл по поверхности σ обозначают удвоенным значком интеграла: 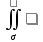 Как и криволинейные, поверхностные интегралы также бывают первого и второго рода. Интеграл первого рода рассмотрим подробнее. Поверхностные интегралы первого рода. Рассмотрим некоторую поверхность σ, состоящую из точек с координатами (x,y,z) Тогда функция трех переменных u=f(x,y,z) будет определена в каждой точке данной поверхности. То есть каждой точке M(x,y,z) поверхности будет соответствовать определённое число u=f(M). Если вернуться к примеру, каждая песчинка или камешек, лежащие на бесконечно малом участке dσ данной поверхности (дна). Следуя общему принципу интегрирования, интеграл 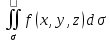 объединяет все эти «камешки и песчинки»по всем бесконечно малым площадям dσ поверхности σ. Можно понять, что при объединяет все эти «камешки и песчинки»по всем бесконечно малым площадям dσ поверхности σ. Можно понять, что при 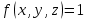 он как раз равен площади самой поверхности: он как раз равен площади самой поверхности: 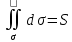 . .§2. Поверхностный интеграл 1-ого рода Если S – кусочногладкая двусторонняя поверхность 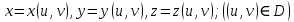 и и 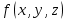 – функция, определенная и неопределенная в точках поверхности S, то – функция, определенная и неопределенная в точках поверхности S, то 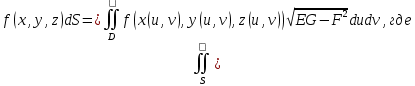 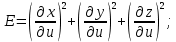 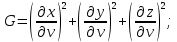 (1) (1)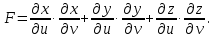 В частности случае, если уравнение поверхности S имеет вид где z(x, y) – однозначная непрерывно дифференцируемая функция, то 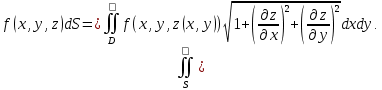 Этот интеграл не зависит от выбора стороны поверхности S. Этот интеграл не зависит от выбора стороны поверхности S. Если функцию 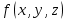 рассматривать как плотность поверхности S в точке рассматривать как плотность поверхности S в точке 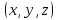 , то интеграл (1) представляет собой массу этой поверхности. , то интеграл (1) представляет собой массу этой поверхности.§3. Применение теории на практике Вычислить следующие поверхностные интегралы 1-ого рода: №4343 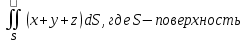 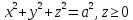 . .Решение: S: 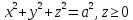 (верхняя полусфера) (верхняя полусфера)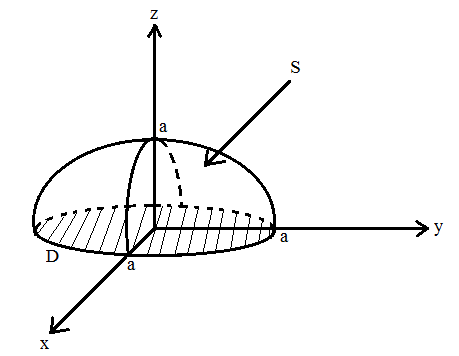 Рис.2 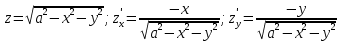 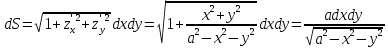 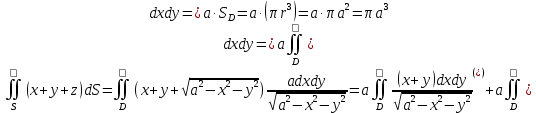 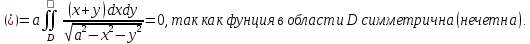 Ответ: 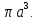 №4344 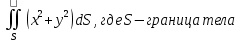 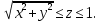 Решение: S: граница 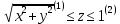 (1) = 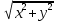 – конус; – конус;(2) = 1 – плоскость. 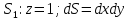 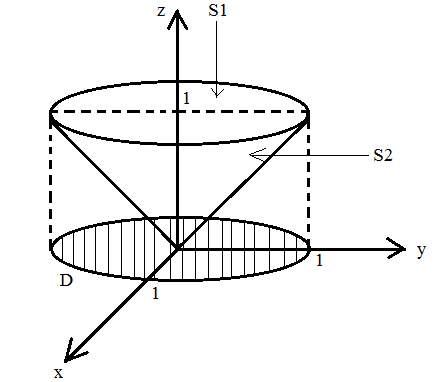 Рис.3 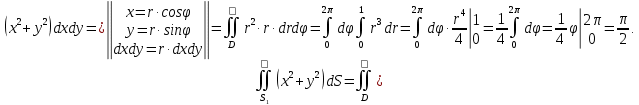 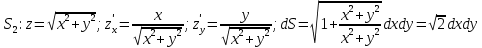 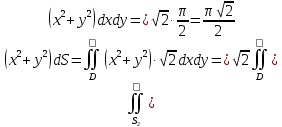 (смотрите предыдущий интеграл). (смотрите предыдущий интеграл).Тогда, 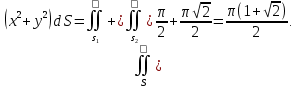 Ответ: 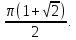 №4345 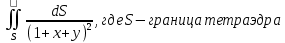 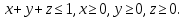 Решение: S: граница 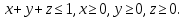 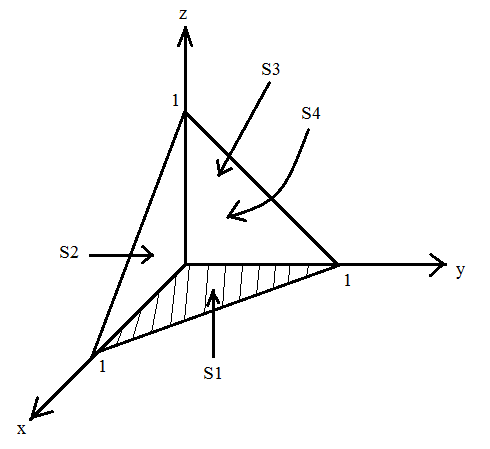 Рис.4 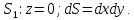 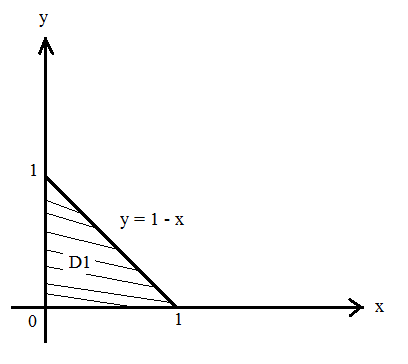 Рис.5 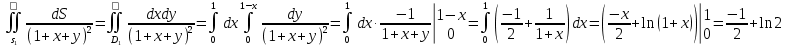 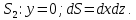 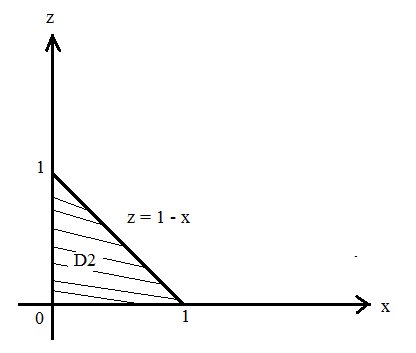 Рис.6 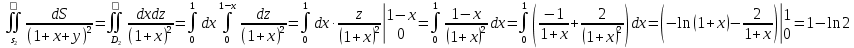 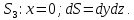 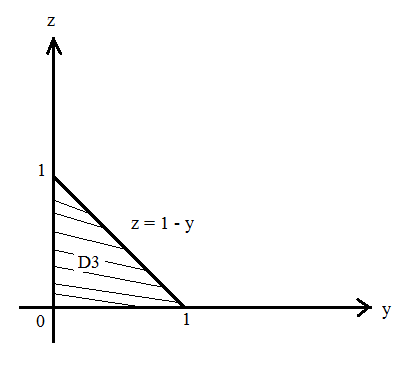 Рис.7 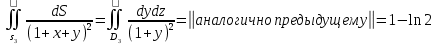 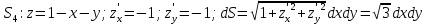  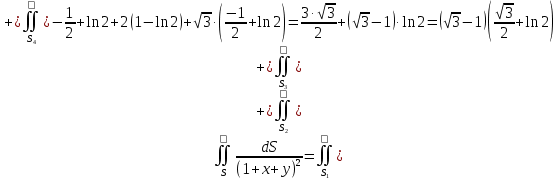 . . Ответ: 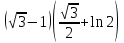 . .№4346 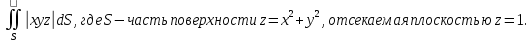 Решение: S: 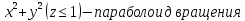 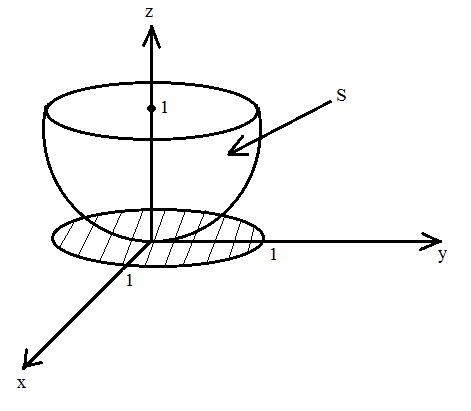 Рис.8 Так как в области функция четная, то достаточно проинтегрировать по области в 1-ой октанте. 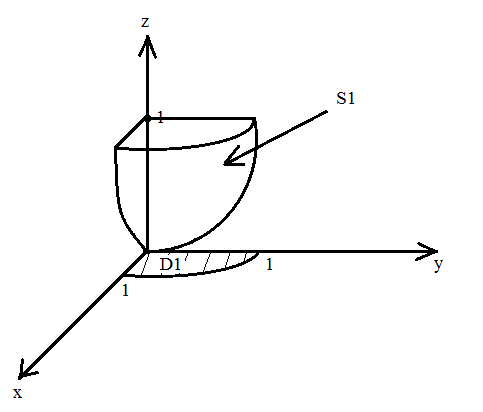 Рис.9 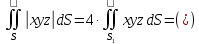 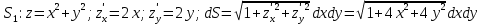 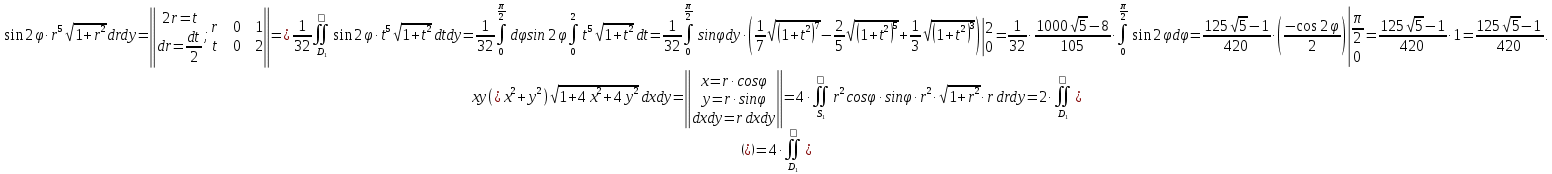 Ответ: 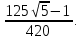 №4347 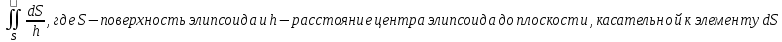 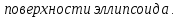 Решение: (1) = 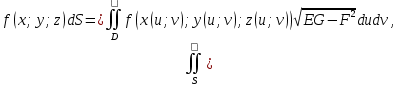 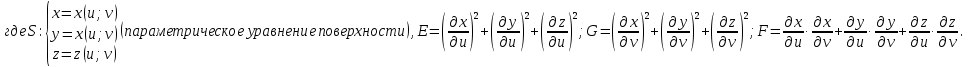 Решение h – определяется формулой 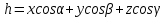 , где , где 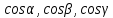 – направляющие косинусы внешней единичной нормали x поверхности в точке (x, y, z). Напишем параметрические уравнения поверхности эллипсоида в виде – направляющие косинусы внешней единичной нормали x поверхности в точке (x, y, z). Напишем параметрические уравнения поверхности эллипсоида в виде 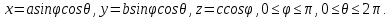 Наша задача заключается в том, чтобы привести поверхностный интеграл к повторному с помощью формулы (1) (положив там 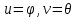 ). Из соображений симметрии можем написать равенство ). Из соображений симметрии можем написать равенство 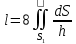 , где , где 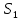 – восьмая часть поверхности эллипсоида, лежащая в первом октанте. Поскольку вектор единичной нормали во всех внутренних точках поверхности – восьмая часть поверхности эллипсоида, лежащая в первом октанте. Поскольку вектор единичной нормали во всех внутренних точках поверхности 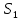 образует с положительным направлением оси Oz острый угол, можем написать формулы образует с положительным направлением оси Oz острый угол, можем написать формулы 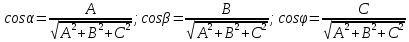 (выбрав перед радикалом знак «+»), где (выбрав перед радикалом знак «+»), где 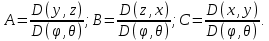 Так как 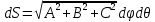 , то, принимая во внимание формулу для расстояния h, имеем: , то, принимая во внимание формулу для расстояния h, имеем: 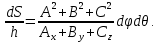 Вычислим значения A, B, C: 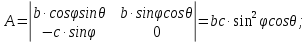 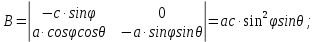 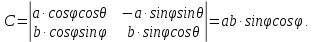 Подставляя в выражение 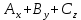 значения x, y, z, зависящие от значения x, y, z, зависящие от 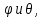 получаем: получаем: 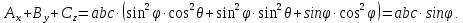 Далее находим: 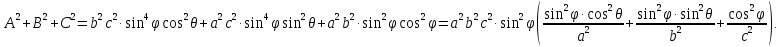 Заменяя поверхностный интеграл соответствующим двойным, получим: 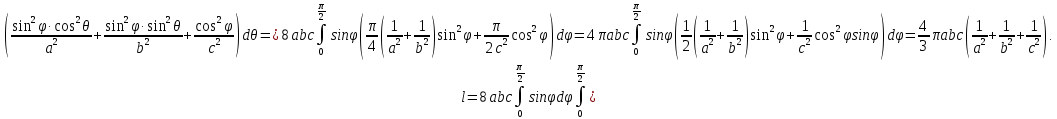 Ответ: 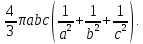 №4348 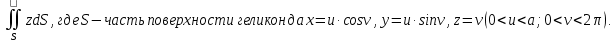 Решение: 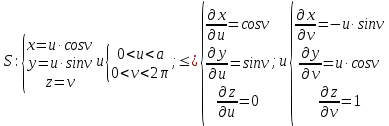 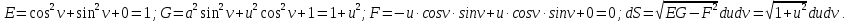 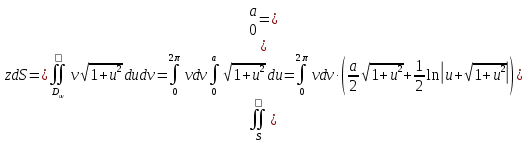 Ответ: 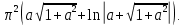 №4349 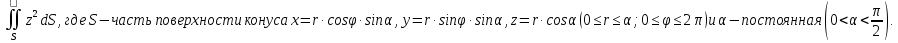 Решение: 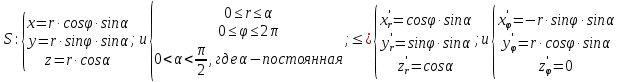 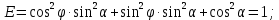 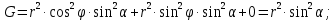 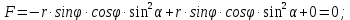 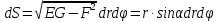 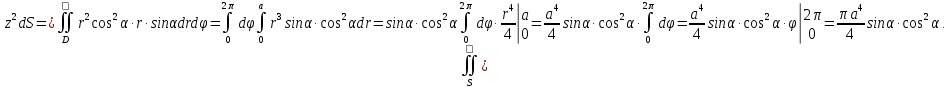 Ответ: 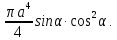 §4. Список литературы Б. П. Демидович. Сборник задач и упражнений Сборник задач и упражнений по математическому анализу: Учеб. пособие. — 13-е изд., испр. — М.: Изд-вo Моск. ун-та, ЧеРо, 1997. — 624 с. |
