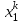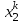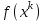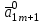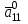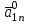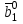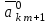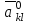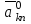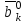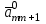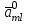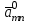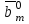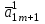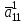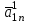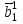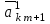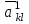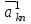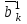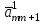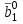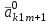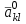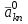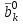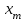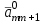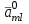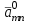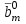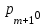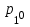Методы оптимизации. Курсовая методы оптимизации. Курсовая работа по предмету Методы оптимизации
 Скачать 347.29 Kb. Скачать 347.29 Kb.
|
1 2 ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Курсовая работа по предмету «Методы оптимизации» студентки 5-го курса Группа № 0-439-81а специальность 220400 «Программное обеспечение вычислительной техники и автоматизированных систем». Нефёдовой А.А. г. Житикара 2005 г. Содержание: Введение Задание на курсовое проектирование Решение задач безусловной оптимизации Анализ задачи Описание алгоритма и его схема Анализ результатов (решение и таблица) Решение задач линейного программирования Анализ задачи Описание алгоритма и его схема Анализ результатов (решение) Заключении Список литературы Приложение к заданию 1 Приложение к заданию 2 1. Введение В наиболее общем смысле теория оптимизации представляет собой совокупность фундаментальных математических результатов и численных методов, ориентированных на нахождение и идентификацию наилучших вариантов из множества альтернатив и позволяющих избежать полного перебора и оценивания возможных вариантов. Процесс оптимизации лежит в основе всей инженерной деятельности. Важность и ценность теории оптимизации заключается в том, что она дает адекватные понятийные рамки для анализа и решения многочисленных задач: в исследовании операций: оптимизация технико-экономических систем, транспортные задачи, управление запасами и т.д.; в численном анализе: аппроксимация, регрессия, решение линейных и нелинейных систем, численные методы, включая методы конечных элементов и т.д.; в автоматике: распознавание образов, оптимальное управление, фильтрация, управление производством, робототехника и т.д.; в математической экономике: решение больших макроэкономических моделей, моделей предпринимательства, теория принятия решений и теория игр. Постановка каждой задачи оптимизации (ЗО) включает в себя два объекта: множество допустимых решений и целевую функцию (функционал), которую следует минимизировать или максимизировать на указанном множестве. С этой общей точки зрения и рассматриваются различные классы экстремальных задач, составляющие предмет линейного, нелинейного, динамического программирования, вариационного исчисления и теории оптимального управления. 2. Задание на курсовое проектирование: Найти точку минимума функции: 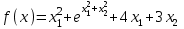 Решить задачу линейного программирования 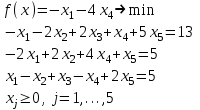 3. Решение задач безусловной оптимизации 3.1 Анализ задачи Данная задача является задачей оптимизации без ограничений или задачей безусловной оптимизации. Данная функция является выпуклой на множестве D, так как все угловые миноры матрицы Гессе – матрицы вторых производных положительны при 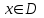 . Для решения данной задачи выбран метод Коши. . Для решения данной задачи выбран метод Коши.3.2 Описание алгоритма и его схема Метод наискорейшего спуска (метод Коши) Известный французский математик Коши Огюстен Луи (21.08.1789–23.05.1857) первым использовал аналогичный алгоритм для решения системы линейных уравнений. В этом широко используемом методе (МК) 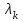 выбираются так, чтобы минимизировать функцию по выбираются так, чтобы минимизировать функцию по 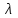 : :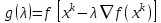 на множестве значений 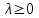 (одномерная минимизация). (одномерная минимизация).Алгоритм Коши. Ш. 1 Выбрать начальную точку 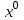 . .Ш. 2 На 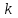 -ой итерации, где -ой итерации, где 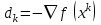 , найти такое , найти такое 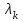 , что , что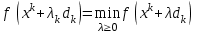 . .Положить 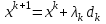 . .Ш. 3 Проверка критерия останова. Да: окончание поиска 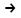 конец. Нет: конец. Нет: 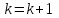 , , 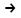 Ш. 2. Ш. 2.Определение. Будем говорить, что алгоритм А глобально сходится, если для любой выбранной исходной точки 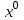 последовательность последовательность 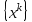 , порожденная точками , порожденная точками 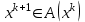 , сходится к точке, удовлетворяющей необходимым условиям оптимальности. , сходится к точке, удовлетворяющей необходимым условиям оптимальности. Замечание. МК обладает глобальной сходимостью, но это не означает обязательного получения глобального экстремума функции 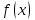 . Если . Если 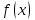 дважды дифференцируема в стационарной точке дважды дифференцируема в стационарной точке 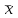 и гессиан и гессиан 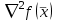 положительно определен, то положительно определен, то 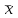 - локальный минимум ЦФ. И только если - локальный минимум ЦФ. И только если 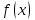 является выпуклой функцией, то является выпуклой функцией, то 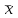 является точкой глобального минимума является точкой глобального минимума 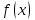 . .МК обладает устойчивостью, т.е. при достаточно малом значении 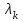 обеспечивается выполнение неравенства: обеспечивается выполнение неравенства: 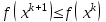 . .МК позволяет существенно уменьшить значение ЦФ (быстро спуститься на "дно оврага") при движении из точек, расположенных на значительных расстояниях от точки 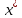 , но в дальнейшем может произойти "зацикливание". Поэтому МК часто используются совместно с другими градиентными методами (например, методом Ньютона) в качестве начальной процедуры. , но в дальнейшем может произойти "зацикливание". Поэтому МК часто используются совместно с другими градиентными методами (например, методом Ньютона) в качестве начальной процедуры.Недостаток: для некоторых типов функций сходимость может оказаться медленной. В самом деле, если 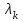 минимизирует функцию минимизирует функцию 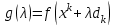 , то должно быть , то должно быть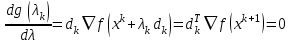 , ,откуда вытекает равенство: 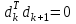 , ,которое доказывает, что последовательные направления ортогональны. В случае ярко выраженной нелинейности ("овражности") ЦФ происходит "зацикливание". Сравнение методов безусловной оптимизации Предполагается, что выполняются следующие условия: 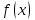 дважды дифференцируема; гессиан дважды дифференцируема; гессиан 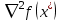 положительно определен. положительно определен.Метод наискорейшего спуска (метод Коши). Последовательность 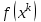 удовлетворяет неравенству: удовлетворяет неравенству: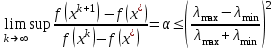 , ,где 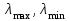 - соответственно наибольшее и наименьшее собственные значения матрицы Гессе - соответственно наибольшее и наименьшее собственные значения матрицы Гессе 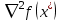 , вычисленные в точке , вычисленные в точке 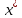 . .Таким образом, в худшем случае имеет место линейная сходимость, для которой коэффициент асимптотической сходимости 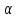 (называемый отношением Канторовича) непосредственно связан с (называемый отношением Канторовича) непосредственно связан с 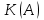 - обусловленностью матрицы - обусловленностью матрицы 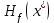 . .Для плохо обусловленной функции (овражного типа) сходимость может быть очень медленной ( 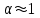 ). ).Ускоренные методы наискорейшего спуска. Для ускоренного метода второго порядка имеем 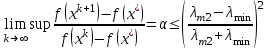 , ,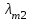 - второе наибольшее собственное значение - второе наибольшее собственное значение 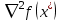 . В двумерном случае имеем . В двумерном случае имеем 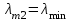 , и следовательно, ускоренный метод второго порядка имеет сходимость высшего порядка, что очень эффективно. Однако в размерностях выше 2-ой сходимость методов с , и следовательно, ускоренный метод второго порядка имеет сходимость высшего порядка, что очень эффективно. Однако в размерностях выше 2-ой сходимость методов с 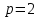 может практически быть такой же плохой, как и в обычном методе, т.к. 2-ое собственное значение может мало отличаться от может практически быть такой же плохой, как и в обычном методе, т.к. 2-ое собственное значение может мало отличаться от 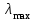 . .При 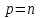 (размерность производства) имеем суперлинейную сходимость. Но при этом на каждой итерации требуется применение ( (размерность производства) имеем суперлинейную сходимость. Но при этом на каждой итерации требуется применение (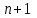 ) одномерных минимизаций. В таком случае метод становится эквивалентным методу сопряженного градиента. ) одномерных минимизаций. В таком случае метод становится эквивалентным методу сопряженного градиента.Метод Ньютона. Обладает квадратичной локальной сходимостью. На практике глобальная сходимость не гарантируется. Методы сопряженных направлений (относительно метода Флетчера-Ривза). Доказано, что 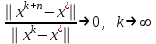 , ,т.е. последовательность 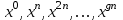 сходится к сходится к 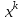 суперлинейно. суперлинейно.Если 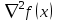 удовлетворяет условию Липшица удовлетворяет условию Липшица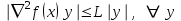 в окрестности точки 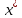 , то имеем квадратичную сходимость по n шагам: , то имеем квадратичную сходимость по n шагам: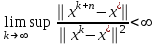 . .Квазиньютоновские методы (применительно к алгоритму ДФП). Сходимость суперлинейная: 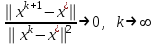 . .Если, кроме того, 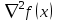 удовлетворяет условию Липшица в окрестности точки удовлетворяет условию Липшица в окрестности точки 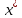 , то сходимость к , то сходимость к 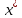 квадратичная: квадратичная: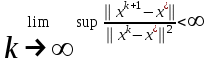 . .Преимущества квазиньютоновских методов по сравнению с методами сопряженных градиентов: требуют в 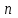 раз меньше этапов (шагов), т.е. в раз меньше этапов (шагов), т.е. в 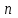 раз меньше числа одномерных минимизаций. Сходимость для одного и того же поведения - квадратичная или суперлинейная. раз меньше числа одномерных минимизаций. Сходимость для одного и того же поведения - квадратичная или суперлинейная.Недостатки. загрузка памяти пропорциональна 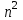 ; ;объем вычислений пропорционален 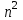 . .3.3 Решение: 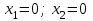 Вычислим компоненты градиента: 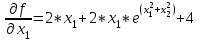 ; ; 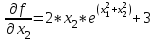 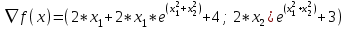 , , 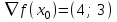 Находим 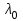 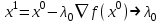 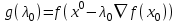 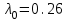 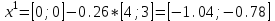 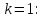 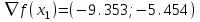 Критерий останова : 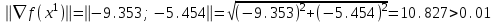 Данные, полученные при проведении дальнейшего поиска приведены в таблице
Решение задач линейного программирования 4.1 Анализ задачи. Задачами линейного программирования (ЛП) называются задачи оптимизации, в которых ограничения, представленные в виде неравенств или равенств, и целевая функция линейны. Данная задача – линейная. Данная задача приведена к стандартному виду. В данной задаче не выделен базис. Для того, чтобы выделить базис, нужно преобразовать систему так, чтобы базисные переменные встречались только в одном неравенстве и с коэффициентом 1. Делается это путем вычитания ограничений друг из друга с умножение на соответствующие константы. После этого базисные переменные выражаются через свободные и подставляются в целевую функцию. Теперь, когда в целевой функции остались только свободные переменные, можно приступать к решению. Нужно проверить, является ли начальное базисное решение допустимым (приравнять свободные переменные к нулю). Если все переменные неотрицательные, то базис допустим. если же нет, то нужно использовать другие переменные для выделения базиса. Описание алгоритма и его схема Основы симплекс–метода Рассмотрим общую задачу линейного программирования с m ограничениями и n переменными, записанную в стандартной (канонической) форме: 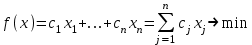 при ограничениях: 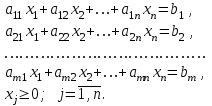 (1) (1)Как правило, число уравнений задачи меньше числа переменных (т.е. 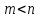 ), поэтому множество ее допустимых решений бесконечно. Следовательно, выбор наилучшего допустимого решения, минимизирующего ЦФ ), поэтому множество ее допустимых решений бесконечно. Следовательно, выбор наилучшего допустимого решения, минимизирующего ЦФ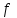 (x), нетривиален. (x), нетривиален. Известен классический метод решения систем линейных уравнений – метод Гаусса–Жордана. Основная идея этого метода состоит в сведении системы mуравнений с nнеизвестными к каноническому виду при помощи элементарных операций над строками. При использовании первых mпеременных 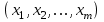 такая система имеет следующий вид: такая система имеет следующий вид: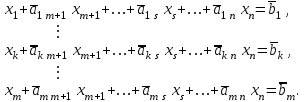 (2) (2)Или (2) можно переписать следующим образом: 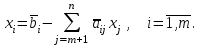 (3) (3)Переменные 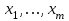 , входящие с единичными коэффициентами только в одно уравнение системы (2) или (3), с нулевыми – в остальные, называются базисными или зависимыми. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. , входящие с единичными коэффициентами только в одно уравнение системы (2) или (3), с нулевыми – в остальные, называются базисными или зависимыми. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Остальные 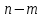 переменных переменных 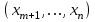 называются небазисными или независимыми переменными. называются небазисными или независимыми переменными.При записи системы в каноническом виде все ее решения можно получить, присваивая независимым переменным произвольные значения и решая затем получающуюся систему относительно зависимых переменных. Для приведения системы к каноническому виду можно использовать 2 типа элементарных операций над строками: умножение любого уравнения системы на положительное или отрицательное число; прибавление к любому уравнению другого уравнения системы, умноженного на положительное или отрицательное число. Базисным решением системы (2) называется решение, полученное при нулевых значениях небазисных переменных. Например: в системе (2) одно из базисных решений задается как: 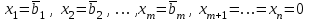 . (4) . (4)Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных 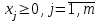 , что эквивалентно условию неотрицательности , что эквивалентно условию неотрицательности 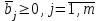 . .Допустимое базисное решение является угловой точкой допустимого множества 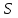 задачи линейного программирования и называется иногда опорным планом. задачи линейного программирования и называется иногда опорным планом.Если среди неотрицательных чисел 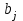 в (2) есть равные нулю, то допустимое базисное решение называется вырожденным (вырожденной угловой точкой) и соответствующая задача линейного программирования называется вырожденной. в (2) есть равные нулю, то допустимое базисное решение называется вырожденным (вырожденной угловой точкой) и соответствующая задача линейного программирования называется вырожденной.В основе симплекс–метода (СМ) лежит следующая теорема. Теорема. Если ЗЛП разрешима, то экстремум целевой функции 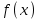 достигается хотя бы в одной из угловых точек допустимого множества достигается хотя бы в одной из угловых точек допустимого множества 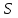 этой задачи. этой задачи.Так как различные базисные решения системы (2) соответствуют различным вариантам выбора 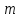 из общего числа из общего числа 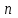 переменных переменных 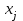 , то число допустимых базисных решений (угловых точек) не превышает , то число допустимых базисных решений (угловых точек) не превышает 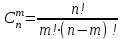 . .Поэтому ЗЛП можно решать посредством перебора конечного числа угловых точек допустимого множества 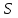 , сравнивая значения целевой функции в этих точках – наихудший вариант. , сравнивая значения целевой функции в этих точках – наихудший вариант.Пример: Если 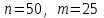 (задача небольшой размерности), то ЭВМ, выполняя 105 переборов варианта в 1 секунду, будет искать решение 106 лет. (задача небольшой размерности), то ЭВМ, выполняя 105 переборов варианта в 1 секунду, будет искать решение 106 лет.Идея СМ состоит в направленном переборе угловых точек допустимого множества 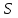 с последовательным уменьшением целевой функции с последовательным уменьшением целевой функции 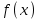 . .СМ разработан Дж. Данцигом. Наиболее простой метод, используемый для решения ЗЛП, - это симплексный метод Данцига. Здесь начало координат переносится в угловую точку допустимой области и рассматриваются линии, соединяющие эту угловую точку со смежными угловыми точками. Исследуется вариация целевой функции 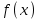 вдоль этих линий, и если какая-нибудь из них дает улучшение, начало координат переносится в угловую точку, в которую ведется линия. Процесс затем повторяется для новой угловой точки и прекращается, когда достигается угловая точка, где вдоль этих линий, и если какая-нибудь из них дает улучшение, начало координат переносится в угловую точку, в которую ведется линия. Процесс затем повторяется для новой угловой точки и прекращается, когда достигается угловая точка, где 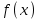 не увеличивается (не уменьшается) вдоль любой такой линии. не увеличивается (не уменьшается) вдоль любой такой линии. Описание симплекс–методаПредположим, что ЗЛП (1) является невырожденной, а базисное решение (4) – допустимым; обозначим его: 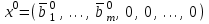 . (5) . (5)Используя соотношение (3), выразим целевую функцию из (1) через свободные переменные 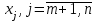 : :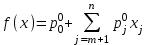 , (6) , (6)где 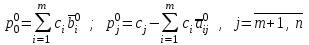 . .Справедливы следующие утверждения: а) если в (6) все коэффициенты 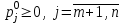 , то в угловой точке (5) достигается минимум целевой функции , то в угловой точке (5) достигается минимум целевой функции 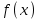 из (1) на допустимом множестве из (1) на допустимом множестве 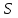 ЗЛП (1) и этот минимум равен ЗЛП (1) и этот минимум равен 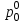 ; ;б) если среди отрицательных коэффициентов 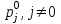 из (6) есть такой (например из (6) есть такой (например 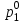 ), что в (2) все коэффициенты ), что в (2) все коэффициенты 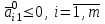 , то целевая функция , то целевая функция 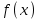 не ограничена снизу на не ограничена снизу на 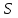 и задача (1) не имеет решений; и задача (1) не имеет решений;в) если хотя бы один из коэффициентов 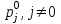 в (6) отрицателен (например, в (6) отрицателен (например, 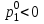 ) и при этом среди коэффициентов ) и при этом среди коэффициентов 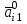 в (2) есть хотя бы один положительный, то существует угловая точка в (2) есть хотя бы один положительный, то существует угловая точка  такая, что такая, что 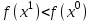 . . В случаях (а) и (б) процесс решения ЗЛП заканчивается. Рассмотрим подробнее случай (в). Пусть в (6) коэффициент 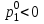 и в (2) имеются положительные коэффициенты и в (2) имеются положительные коэффициенты 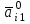 . Найдем номер . Найдем номер 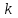 базисной переменной из условия: базисной переменной из условия: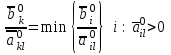 , (7) , (7)где минимум берется по всем номерам 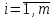 , для которых , для которых 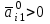 . .Найдем решение системы ограничений из (1), т. е.: 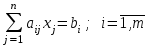 , ,считая свободными переменные: 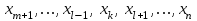 , т. е. поменяв местами свободную переменную , т. е. поменяв местами свободную переменную 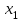 с базисной переменной с базисной переменной 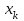 . Система уравнений (2) в этом случае запишется следующим образом: . Система уравнений (2) в этом случае запишется следующим образом: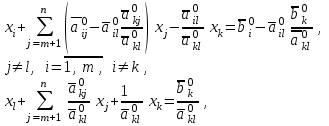 (8) (8)а зависимость целевой функции от новых свободных переменных примет вид: 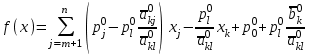 . (9) . (9)Компоненты нового базисного решения 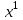 можно найти, приравняв нулю свободные переменные можно найти, приравняв нулю свободные переменные 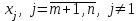 и и 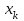 и найдя при этом условии значения базисных переменных из (8). Базисное решение и найдя при этом условии значения базисных переменных из (8). Базисное решение 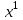 является допустимым, то есть угловой точкой множества ОДР является допустимым, то есть угловой точкой множества ОДР 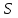 , причем выполнение неравенства , причем выполнение неравенства 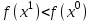 приводит к новой симплекс–таблице (СТ), для определения элементов которой необходимо выполнить следующие операции: приводит к новой симплекс–таблице (СТ), для определения элементов которой необходимо выполнить следующие операции:Поменять местами переменные 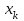 и и 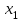 , остальные переменные оставить на прежних местах. , остальные переменные оставить на прежних местах.Таблица 1
На место опорного элемента поставить число 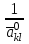 . .На остальных местах разрешающей (опорной) строки записать соответствующие элементы исходной таблицы, деленные на опорный элемент. На свободные места разрешающего столбца поставить со знаком минус соответствующие элементы исходной таблицы, деленные на опорный элемент. Оставшиеся свободные места в новой СТ заполнить построчно следующим образом: из строки элементов исходной таблицы вычесть произведение ее элемента из разрешающего столбца на уже заполненную разрешающую строку новой таблицы. Например, для строки 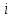 –ой базисной переменной имеем: –ой базисной переменной имеем: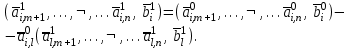 Знак «» стоит на месте элемента разрешающего столбца, заполненного согласно определению операции 4. По знакам коэффициентов в системе (8) и выражению для целевой функции (9) можно сделать одно из трех приведенных выше заключений, как это было сделано для угловой точки 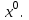 В случае (в) следует совершить переход к очередной точке В случае (в) следует совершить переход к очередной точке 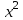 , аналогичный переходу от , аналогичный переходу от 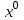 к к 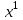 , и т. д. , и т. д.Так как число угловых точек допустимого множества 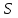 не превышает не превышает 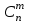 , то случай (в) может повторяться конечное число раз, т. е. в результате конечного числа шагов перехода к новой угловой точке будет найдено решение ЗЛП либо будет сделано заключение о том, что она не имеет решения. , то случай (в) может повторяться конечное число раз, т. е. в результате конечного числа шагов перехода к новой угловой точке будет найдено решение ЗЛП либо будет сделано заключение о том, что она не имеет решения.Реализация описанного выше симплекс–метода значительно упрощается при использовании симплекс–таблицы. Записав коэффициенты уравнений (2) и (6) соответствующим образом, получим СТ задачи (1) для угловой точки 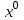 из (5). из (5).Таблица 2
Рассмотрим переход от СТ–1, соответствующей угловой точке 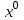 к СТ-2 для угловой точки к СТ-2 для угловой точки 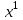 . .Пусть номера 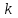 и и 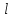 определены так, как это сделано выше. Элемент определены так, как это сделано выше. Элемент 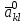 , а также строка и столбец СТ–1, на пересечении которых он стоит, называются разрешающими или опорными. Из формул (8) и (9) следует, что преобразование исходной СТ с опорным элементом , а также строка и столбец СТ–1, на пересечении которых он стоит, называются разрешающими или опорными. Из формул (8) и (9) следует, что преобразование исходной СТ с опорным элементом 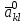 (см. Таблицу 2). (см. Таблицу 2).4.3 Решение: 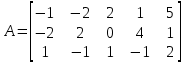 В качестве начальной угловой точки 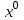 используем базисное решение, соответствующее свободным переменным используем базисное решение, соответствующее свободным переменным 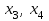 . .Возьмем 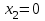 и и 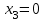 . .Приведем систему к виду, где базисными являются переменные 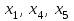 . .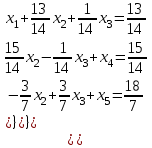 В итоге получим 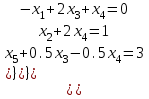 Получим 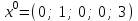 Исключив базисные переменные в выражение для целевой функции, получим: 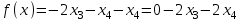 Составим симплекс-таблицу, соответствующую точке 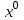
Среди коэффициентов нижней строки таблицы есть отрицательные, следовательно угловая точка 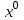 не является решением задачи. не является решением задачи.Составим новую симплекс-таблицу. Найдем опорный элемент. Возьмем в качестве опорного столбца столбец, соответствующий свободной переменной 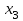 . Так как опорный элемент должен быть больше 0, то в качестве опорной строки берется строка, соответствующая базисной переменной . Так как опорный элемент должен быть больше 0, то в качестве опорной строки берется строка, соответствующая базисной переменной 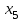 . Опорный элемент равен 0,5. . Опорный элемент равен 0,5.Для определения элементов симплекс-таблицы необходимо выполнить следующие операции: а) Поменять местами переменные 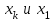 , остальные переменные оставить на прежних местах , остальные переменные оставить на прежних местах
б) На место опорного элемента поставить число 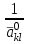 . .в) На остальных местах разрешающей (опорной) строки записать соответствующие элементы исходной таблицы, деленные на опорный элемент г) На свободные места разрешающего столбца поставить со знаком минус соответствующие элементы исходной таблицы, деленные на опорный элемент д) Оставшиеся свободные места в новой симплекс-таблице заполнить построчно следующим образом: из строки элементов исходной таблицы вычесть произведение ее элемента из разрешающего столбца на уже заполненную разрешающую строку новой таблицы. По правилам, описанным выше, заполним новую симплекс-таблицу
Среди коэффициентов нижней строки таблицы есть отрицательные, следовательно угловая точка 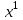 не является решением задачи. не является решением задачи.Составим новую симплекс-таблицу. Найдем опорный элемент. Возьмем теперь в качестве опорного столбца столбец, соответствующий свободной переменной 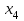 . Так как опорный элемент должен быть больше 0, то в качестве опорной строки берется строка, соответствующая базисной переменной . Так как опорный элемент должен быть больше 0, то в качестве опорной строки берется строка, соответствующая базисной переменной 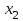 . Опорный элемент равен 2. . Опорный элемент равен 2.По правилам, описанным выше, заполним новую симплекс-таблицу
В данной таблице оба коэффициента в последней строке положительны, поэтому угловая точка 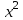 , соответствующая свободным переменным , соответствующая свободным переменным 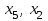 является минимумом целевой функции является минимумом целевой функции 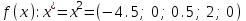 . Минимальное значение . Минимальное значение 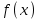 со знаком минус записано в правом нижнем углу СТ, поэтому со знаком минус записано в правом нижнем углу СТ, поэтому 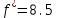 . .5. Заключение В результате выполнения курсовой работы был изучены методы решения задач безусловной оптимизации и задач линейного программирования. Для безусловной оптимизации были рассмотрены и сравнены несколько методов, был выбран метод Коши. Для линейного программирования был выбран симплекс-метод. В данной работе имеются программы вычисления значения оптимума заданных функций. 1 2 |