курсовая. Курсач. Курсовая работа примеры и принципы Алгоритмического анализа Ф. И. О студента Архипов Алексей Владимирович Группа 1Дд

• Название: Курсовая работа примеры и принципы Алгоритмического анализа Ф. И. О студента Архипов Алексей Владимирович Группа 1Дд
• Анкор: курсовая
• Дата: 19.04.2022
• Размер: 249.06 Kb.
• Имя файла: Курсач.docx
• Тип: Курсовая; #485076

Комитет образования и науки Волгоградской области

Государственное автономное профессиональное образовательное учреждение

«Волгоградский социально-педагогический колледж»

КУРСОВАЯ РАБОТА
Примеры и принципы Алгоритмического анализа

Ф.И.О студента: Архипов Алексей Владимирович

Группа 1«Дд»

Специальность 09.02.07 «Информационные системы и программирование»
Руководитель: Гермашев Илья Васильевич
Работа допущена к защите «__»_________20__г
Оценка:

(роспись руководитель)

Волгоград, 2020 г.
Содержание

Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Глава 1. Теоретическая часть . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1

1. 
   Понятие «Алгоритм» и «Алгоритмический анализ» . . . . . . . . . . . . . . . . . .1
   
2. 
   Применение Алгоритмического анализа . . . . . . . . . . . . . . . . . . . . . . . . . . .2
   
3. 
   Анализ алгоритмов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
   
   1. 
      Анализ алгоритмов и производительность . . . . . . . . . . . . . . . . . . . . . 9
      
4. 
   Свойство алгоритмов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10
   
5. 
   Способы описания алгоритмов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11
   
   1. 
      Правила создания блок-схем . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .12
      
   2. 
      Виды алгоритмов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .13
      
6. 
   Алгоритмы объединение-поиск . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .14
   
7. 
   Алгоритмы сортировки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .14
   
   1. 
      Виды алгоритмов сортировки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .15
      
8. 
   Другие алгоритмические инструменты . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
   
   1. 
      Жадные приближенные алгоритмы . . . . . . . . . . . . . . . . . . . . . . . . . . .17
      
   2. 
      Вероятностные алгоритмы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
      
9. 
   Алгоритмы на графах . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .18
   
   1. 
      Виды алгоритмов на графах . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .18
      

1.10 Оценка сложности . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

1. 
   Виды сложности . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .20
   

Глава 2. Практическая часть . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .21

Заключение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .25

Список литературы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .25
Благодаря бурному развитию науки информатики и проникновению её в различные отрасли народного хозяйства слово "алгоритм" стало часто встречающимся и наиболее популярным в житейском плане понятием для большого круга лиц, более того, с переходом к информационному обществу алгоритмы становятся одним из важных факторов цивилизации.

Известно, что математическая теория алгоритмов сложилась вовсе не в связи с сильным развитием информатики и вычислительной техники, а возникла в недрах математической логики, для решения её собственных проблем. Она, прежде всего, оказала большое влияние на мировоззрение математиков и на их науку.

Тем не менее, взаимовлияние теоретических областей, связанных с вычислительной техникой, и теории алгоритмов также, несомненно повлияло.

Теория алгоритмов оказала влияние на теоретическое программирование. В частности, большую роль в теоретическом программировании играют модели вычислительных автоматов, которые, по существу, являются ограничениями тех представительных вычислительных моделей, которые были созданы ранее в теории алгоритмов, трактовка программ, как объектов вычисления, операторы, используемые для составления структурированных программ (последовательное выполнение, разветвление, повторение) пришли в программирование из теории алгоритмов. Обратное влияние выразилось, например, в том, что возникла потребность в создании и развитии теории вычислительной сложности алгоритмов. Таким образом, можно сказать, что теория алгоритмов применяется не только в информатике, но и в других областях знаний.

Глава 1. Теоретическая часть

1. 
   . Понятие «Алгоритма» и «Алгоритмического анализа».
   

Алгоритм — описанная на некотором языке точная конечная система правил, определяющая содержание и порядок действий над некоторыми объектами, строгое выполнение которых дает решение поставленной задачи.

1

Само слово «алгоритм» происходит от имени хорезмского учёного аль-Хорезми. Около 825 года он написал сочинение Китаб аль-джебр валь-мукабала («Книга о сложении и вычитании»), из оригинального названия которого происходит слово «алгебра» (аль-джебр — восполнение). В этой книге впервые дал описание придуманной в Индии позиционной десятичной системы счисления.

Алгоритмический анализ - это универсальный методологический инструмент познания не только в традиционной области вычислений, но и в других областях, ранее казалось бы далеких от точных описаний.

2. 
   . Применение Алгоритмического анализа
   

Применение алгоритмического анализа позволяет составить описание практически любых действий, выполняемых оператором при управлении технологическими процессами. В качестве примера такого описания на рис. IV-4 приведена логическая схема алгоритма действий оператора в ситуации, характеризующейся выходом за нормы регламента температуры пожароопасного продукта, перерабатываемого в экструдере.



Рис. IV-4 Логическая схема алгоритма действий оператора при нарушениях технологического процесса.


2

Анализ алгоритмов деятельности оператора можно проводить на системном и операционно-психологическом уровнях. На системном уровне алгоритм рассматривается как целое и выявляется общая психологическая и физиологическая специфика работы оператора в системе. Операционно-психологический уровень подразумевает расчленение алгоритма на элементарные операции или блоки операций.

В настоящее время наиболее распространеным методом исследования на операционно-психологическом уровне является

операционно-структурный метод описания деятельности человека-оператора, основанный на алгоритмическом описании деятельности.

Можно привести основные определения, на которых базируется этот метод.

1. 
   Алгоритм – точное предписание о выполнении в определенной последовательности элементарных операций ( из системы данных операций) для решения любой из задач, принадлежащих к некоторому классу.
   
2. 
   Понятие «элементарная операция» относительно и зависит от особенностей системы, выполняющей эти операции, Критерием элементарности операции при анализе деятельности человека является его способность выполнять их как единый целостный акт. В качестве элементарных операций при алгоритмическом анализе принимают операторы и логические условия.
   
3. 
   Оператор – элементарное действие, воспринимаемое как единое целое.
   
4. 
   Логическое условие – условие, определяющее, какой из возможных операторов будет иметь место при выполнении или невыполнении этого условия.
   

С помощью алгоритмического анализа решают следующие задачи: исследование влияния сложности алгоритма на качество работы человека-оператора;

3

распределение функций между человеком и машиной, обоснование степени автоматизации трудового процесса на этапе проектирования СЧМ в зависимости

от сложности алгоритма; разработка алгоритмов работы человека-оператора при проектировании СЧМ; проведение инженерно-психологической экспертизы существующих образцов техники на этапах испытаний и эксплуатации в целях выявления наиболее сложных элементов деятельности и планирования на этой основе конструктивных доработок; исследование вопросов профессионального обучения человека-оператора, его подготовки на тренажерах, а также разработка количественных критериев оценки эффективности обучения.

Существует две основные формы записи алгоритмов: логическая схема алгоритма и блочная схема алгоритма.

В логической схеме алгоритмы записываются в строчку, в виде последовательности операторов и логических условий. Операторы обозначаются прописными буквами латинского алфавита, а логические условия – строчными. После каждого логического условия стоит начальная нумерованная стрелка: конечная стрелка с таким же номером стоит перед каким-либо другим членом алгоритма. Работа алгоритма начинается с того, что срабатывает самый левый член схемы.

Если это оператор, то за ним срабатывает тот член схемы, который стоит непосредственно справа.

С позиций алгоритмического анализа похожесть форм определяется единой общей схемой их алгоритмического строения ( рекурсией), расхождение вызвано многообразием форм конкретной реализации алгоритмов. В нем найдется в принципе зеркальное соответствие каждому изображению. Лишь в крошечном уголке зеркала есть малюсенькое пятнышко, в котором отражение не происходит.

На основе данного алгоритмического анализа оценивается степень стереотипности процесса управления, которую можно рассматривать как однозначно детерминированную последовательность реакций на определенный раздражитель.

4

При алгоритмическом описании такой этап деятельности представляется в форме ряда последовательных элементов, между которыми нет членов, определяющих проверяемые логические условия.

В настоящее время алгоритмический анализ приобретает роль универсального методологического инструмента познания не только в традиционной области вычислений, но и в других областях, ранее казалось бы далеких от точных описаний. Происходит новое переосмысливание старых понятий, объяснимое следующей схемой рассуждений. Глубокое проникновение в тайны природы привело к возникновению сложных технических устройств и становлению соответствующего алгоритмического аппарата, однако созданный формальный аппарат приобрел самостоятельный универсальный статус и позволяет с достаточной степенью адекватности анализировать существующие закономерности природы. При таком подходе стержневым моментом является понимание алгоритма как некоторой общей категории. Остановимся на этом более подробно.

Понятие алгоритма относится к фундаментальным понятиям естествознания. История алгоритмов прошла длинный путь от интуитивного понимания и стихийного применения до осознания закономерностей и практического использования в современных ЭВМ. По сути, алгоритмы проявляются в функционировании любой системы, порожденной природой, включая человека и его творения. Развитие науки можно представить как непрерывный процесс уточнения этих алгоритмов и построения соответствующих моделей.
1.3. Анализ алгоритмов

При анализе алгоритма определяется количество «времени», необходимое для его выполнения. Это не реальное число секунд или других промежутков времени, а приблизительное число операций, выполняемых алгоритмом. Число операций и измеряет относительное время выполнения алгоритма. Таким образом, иногда мы будем называть «временем» вычислительную сложность алгоритма. Фактическое количество секунд, требуемое для выполнения алгоритма на ком

5

пьютере, непригодно для анализа, поскольку нас интересует только относительная эффективность алгоритма, решающего конкретную задачу. Мы также увидим, что и вправду время, требуемое на решение задачи, не очень хороший способ измерять эффективность алгоритма, потому что алгоритм не становится лучше, если его перенести на более быстрый компьютер, или хуже, если его исполнять на более медленном.

Что такое анализ?

Анализируя алгоритм, можно получить представление о том, сколько времени займет решение данной задачи при помощи данного алгоритма. Одну и ту же задачу можно решить с помощью различных алгоритмов. Анализ алгоритмов дает нам инструмент для выбора алгоритма.

Результат анализа алгоритмов — не формула для точного количества секунд или компьютерных циклов, которые потребует конкретный алгоритм. Нужно понимать, что разница между алгоритмом, который делает N + 5 операций, и тем, который делает N + 250 операций, становится незаметной, как только N становится очень большим.

Классы входных данных

При анализе алгоритма выбор входных данных может существенно повлиять на его выполнение. Скажем, некоторые алгоритмы сортировки могут работать очень быстро, если входной список уже отсортирован, тогда как другие алгоритмы покажут весьма скромный результат на таком списке. А вот на случайном списке результат может оказаться противоположным. Поэтому не будем ограничиваться анализом поведения алгоритмов на одном входном наборе данных. Практически нужно искать такие данные, которые обеспечивают как самое быстрое, так и самое медленное выполнение алгоритма. Кроме того, полезно оценивать и среднюю эффективность алгоритма на всех возможных наборах данных.

6

Наилучший случай

Время выполнения алгоритма в наилучшем случае очень часто оказывается маленьким или просто постоянным, поэтому подобный анализ проводится редко.

Наихудший случай

Анализ наихудшего случая чрезвычайно важен, поскольку он позволяет представить максимальное время работы алгоритма. При анализе наихудшего случая необходимо найти входные данные, на которых алгоритм будет выполнять больше всего работы.

Средний случай

Анализ среднего случая является самым сложным, поскольку он требует учета множества разнообразных деталей. В основе анализа лежит определение

различных групп, на которые следует разбить возможные входные наборы данных. На втором шаге определяется вероятность, с которой входной набор данных принадлежит каждой группе. На третьем шаге подсчитывается время работы алгоритма на данных из каждой группы. Время работы алгоритма на всех входных данных одной группы должно быть одинаковым, в противном случае группу следует подразбить. Среднее время работы вычисляется по формуле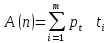



где через n обозначен размер входных данных, через m — число групп. через pi — вероятность того, что входные данные принадлежат группе с номером i, а через ti — время, необходимое алгоритму для обработки данных из группы с номером i.
В большинстве случаев мы будем предполагать, что вероятности попадания входных данных в каждую из групп одинаковы. Другими словами, если групп пять, то вероятность попасть в первую группу такая же, как вероятность попасть

7

во вторую, и т.д., то есть вероятность попасть в каждую группу равна 0.2. В этом случае среднее время работы можно либо оценить по предыдущей формуле, либо воспользоваться эквивалентной ей формулой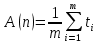



Нижние границы. Дерево решений.

Алгоритм является оптимальным, если любой любой другой алгоритм, решающий данную задачу, работает не быстрее данного. Как узнать оптимальность алгоритма? Для этого мы должны знать минимальное количество операций, необходимое для решения поставленной задачи, которое называется нижней границей. Но для этого нам нужно изучать именно ЗАДАЧУ, а не конкретный алгоритм!


Как пример, рассмотрим анализ процесса сортировки списка из 3 чисел, воспользовавшись бинарным деревом. Такое дерево называется деревом решений.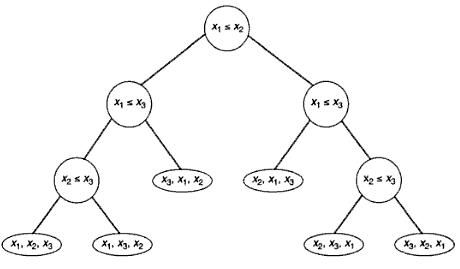


8

Самый длинный путь в данном дереве соответствует наихудшему случаю и наоборот, кратчайший — наилучшему. Средний случай описывается частным от деления числа ребер в дереве на число листов.
Для перестановки 2-х элементов мы имеем 1лист, для N эл-тов, по правилам комбинаторики, N! листов. Число листов на уровне K равно 2k-1, поэтому в нашем дереве решений буде L -уровней, где L — наименьшее целое число, для которого N! ≤ 2L-1. Логарифмируя, получим




В конечном итоге, получаем:



Вот мы и узнали, что любой алгоритм сортировки, порядка О(NlgN) является наилучшим и его можно считать оптимальным, более того, из этого исследования вытекает, что алгоритм, решающий задачу сортировки быстрее О(NlgN) операций, не может работать правильно!

1.3.1. Анализ алгоритмов и производительность

Анализ алгоритмов можно определить как теоретическое исследование производительности компьютерных программ и использования ими ресурсов. Мы сосредоточимся на производительности.

9

Если сверхбыстрая программа выдает неверный результат, это плохая про-грамма. Еще есть такие понятия, как простота, удобство обслуживания, надежность, безопасность, функциональность и удобство для пользователя. Все они гораздо важнее производительности. Вот например, Эван Шпигель решил перепроектировать Snapchat. Зачем? Snapchat уже работает отлично, как было задумано. Просто пользователи жаловались на определенную сложность работы с приложением, и Эван решил сделать его проще в использовании. Удобство явно перевешивает эффективность алгоритмов. Очевидно, что производительность – это не самая важная вещь. Тогда почему мы о ней говорим? Дело в том, что иногда удобство использования напрямую связано с производительностью. Представим, что мы смотрии на веб-страницу, которая загружается уже целую вечность. В режиме реального времени недостаточно быстрое приложение считается неработающим. Слишком большое использование памяти тоже ухудшает пользовательский опыт.

1.4. Свойство алгоритмов

Существует множество определений понятия «алгоритм»:

1. 
   «процедура, которая принимает любой из возможных входных экземпляров задачи и преобразует его в соответствии с требованиями, указанными в условии задачи».
   
2. 
   «точное предписание, однозначно определяющее вычислительный процесс, ведущий от варьируемых начальных данных к искомому результату».
   
3. 
   «конечный набор правил, однозначно раскрывающих содержание и последовательность выполнения операций для систематического решения определенного класса задач за конечное число шагов».
   

Из определений вытекают свойства алгоритма:

1. 
   Дискретность. В определениях 3 и 4 говорится, что алгоритм состоит из отдельных действий или правил. Алгоритм обладает дискретностью, если
   

10
его можно разделить на отдельные этапы (части, команды).

2. 
   Детерминированность (определенность). Алгоритм обладает свойством детерминированности, если для одних и тех же наборов исходных данных он будет выдавать один и тот же результат, т.е. результат однозначно определяется исходными данными (на это свойство указывается в определении 3).
   
3. 
   Результативность. Свойство результативности означает, что алгоритм должен выдавать результат за конечное число шагов. О том, что число шагов должно быть конечным говорится в определениях 3 и 4.
   
4. 
   Массовость. В определениях 1, 2, 3 говорится о некоторых классах задач (входных экземплярах задачи, варьируемых начальных данных) на которых алгоритм должен работать алгоритм. Это означает, что набор исходных данных, на которых алгоритм должен выдавать верное решение, заранее ограничен.
   
5. 
   Правильность. Под правильностью понимается соответствие результатов работы алгоритма условию задачи (определение 1). Казалось бы, очень сомнительное свойство, ведь выше было описано свойство результативности, однако, программа должна не просто выдавать результат, а результат правильный.
   

1.5. Способы описания алгоритмов.

Словесная форма записи алгоритмов обычно используется для алгоритмов, ориентированных на исполнителя-человека. Команды такого алгоритма выполняются в естественной последовательности, если не оговорено противного.

Графическая запись с помощью блок-схем осуществляется рисованием последовательности геометрических фигур, каждая из которых подразумевает выполнение определенного действия алгоритма. Порядок выполнения действий указывается стрелками. Графическая запись алгоритма имеет ряд преимуществ: каждая операция вычислительного процесса изображается отдельной геометри

11

ческой фигурой и графическое изображение алгоритма наглядно показывает разветвления путей решения задачи в зависимости от различных условий, повторение отдельных этапов вычислительного процесса и другие детали.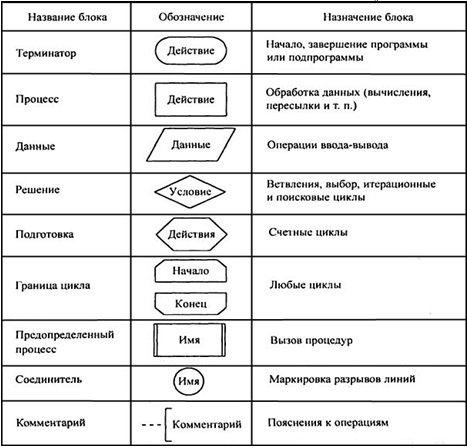


1.5.1 Правила создания блок-схем

1. 
   Линии, соединяющие блоки и указывающие последовательность связей между ними, должны проводится параллельно линиям рамки.
   
2. 
   Стрелка в конце линии может не ставиться, если линия направлена слева направо или сверху вниз.
   
3. 
   В блок может входить несколько линий, то есть блок может являться
   

12
преемником любого числа блоков.

4. 
   Из блока (кроме логического) может выходить только одна линия.
   
5. 
   Логический блок может иметь в качестве продолжения один из двух блоков, и из него выходят две линии.
   
6. 
   Если на схеме имеет место слияние линий, то место пересечения выделяется точкой. В случае, когда одна линия подходит к другой и слияние их явно выражено, точку можно не ставить.
   
7. 
   Схему алгоритма следует выполнять как единое целое, однако в случае необходимости допускается обрывать линии, соединяющие блоки.
   

1.5.2 Виды алгоритмов

В линейном алгоритме операции выполняются последовательно, в порядке их записи. Каждая операция является самостоятельной, независимой от каких-либо условий. На схеме блоки, отображающие эти операции, располагаются в линейной последовательности.

В алгоритме с ветвлением предусмотрено несколько направлений (ветвей). Каждое отдельное направление алгоритма обработки данных является отдельной ветвью вычислений. Направление ветвления выбирается логической проверкой, в результате которой возможны два ответа:

1.«да» — условие выполнено.

2.«нет» — условие не выполнено.

Циклические алгоритмы содержат цикл – это многократно повторяемый участок алгоритма. Различают циклы с предусловием и постусловием. Также циклы бывают детерминированные и итерационные. Цикл называется детерминированным, если число повторений тела цикла заранее известно или определено. Цикл называется итерационным, если число повторений тела цикла заранее неизвестно, а зависит от значений параметров (некоторых переменных), участвующих в вычислениях.

13
1.6. Алгоритмы объединение-поиск.

Первый шаг в процессе разработки эффективного алгоритма, решение данной задачи – реализация простого алгоритма ее решения, если нужно решить несколько вариантов конкретной задачи, которые оказываются простыми, это может быть выполнено посредством простой реализации. Если требуется более сложный алгоритм, то простая реализация предоставляет возможность проверить правильность работы алгоритма для простых случаев и может служить отправной точкой для оценки характеристик производительности, эффективность всегда является предметом заботы, но первоочередная забота при разработке первой программы решения задачи – убедиться в том, что программа обеспечивает правильное решение.

Первое что приходит в голову – как-либо сохранить все вводимые пары, а затем создать функцию для их просмотра, что бы попытаться выяснить, связанна ли следующая пара объектов, однако придётся использовать другой подход. Во-первых, количество пар может быть достаточно велико, что не может позволит сохранить их все в памяти в используемом на практике приложением. Во-вторых, что гораздо важнее, не существует никакого простого метода, который сам по себе позволяет определить связаны ли два объекта в наборе всех соединений, даже если бы удалось их все сохранить.

1.7. Алгоритмы сортировки.

Алгоритм сортировки — это алгоритм для упорядочивания элементов в списке, в случае, когда элемент списка имеет несколько полей, поле, служащее критерием порядка, называется ключом сортировки. На практике в качестве ключа часто выступает число, а в остальных полях хранятся какие-либо данные, не влияющие на работу алгоритма.

По некоторым источникам, программа сортировки стала первой программой для вычислительных машин. Некоторые создатели ЭВМ, в частности разработчики EDVAC, называли сортировки данных наиболее характерной нечисловой

14
задачей для вычислительных машин.

1.7.1. Виды алгоритмов сортировки.

1. Сортировка пузырьком — один из самых известных алгоритмов сортировки. Здесь нужно последовательно сравнивать значения соседних элементов и менять числа местами, если предыдущее оказывается больше последующего. Таким образом элементы с большими значениями оказываются в конце списка, а с меньшими остаются в начале.
Этот алгоритм считается учебным и почти не применяется на практике из-за низкой эффективности: он медленно работает на тестах, в которых маленькие элементы (их называют «черепахами») стоят в конце массива. Однако на нём основаны многие другие методы, например, шейкерная сортировка и сортировка расчёской.

2. 
   Шейкерная сортировка отличается от пузырьковой тем, что она двунаправленная: алгоритм перемещается не строго слева направо, а сначала слева направо, затем справа налево.
   
3. 
   Сортировка расчёской — улучшение сортировки пузырьком. Её идея состоит в том, чтобы «устранить» элементы с небольшими значения в конце массива, которые замедляют работу алгоритма. Если при пузырьковой и шейкерной сортировках при переборе массива сравниваются соседние элементы, то при «расчёсывании» сначала берётся достаточно большое расстояние между сравниваемыми значениями, а потом оно сужается вплоть до минимального.
   

Первоначальный разрыв нужно выбирать не случайным образом, а с учётом специальной величины — фактора уменьшения, оптимальное значение которого равно 1,247. Сначала расстояние между элементами будет равняться раз

15

меру массива, поделённому на 1,247; на каждом последующем шаге

расстояние будет снова делиться на фактор уменьшения — и так до окончания работы алгоритма.

4. 
   При сортировке вставками массив постепенно перебирается слева направо. При этом каждый последующий элемент размещается так, чтобы он оказался между ближайшими элементами с минимальным и максимальным значением.
   
5. 
   Сортировка выбором - нужно рассмотреть подмножество массива и найти в нём максимум (или минимум). Затем выбранное значение меняют местами со значением первого неотсортированного элемента. Этот шаг нужно повторять до тех пор, пока в массиве не закончатся неотсортированные подмассивы.
   
6. 
   Быстрая сортировка - этот алгоритм состоит из трёх шагов. Сначала из массива нужно выбрать один элемент — его обычно называют опорным. Затем другие элементы в массиве перераспределяют так, чтобы элементы меньше опорного оказались до него, а большие или равные — после. А дальше рекурсивно применяют первые два шага к подмассивам справа и слева от опорного значения.
   

Быструю сортировку изобрели в 1960 году для машинного перевода: тогда словари хранились на магнитных лентах, а сортировка слов обрабатываемого текста позволяла получить переводы за один прогон ленты, без перемотки назад

7. 
   Сортировка слиянием – она пригодится для таких структур данных, в которых доступ к элементам осуществляется последовательно
   

16

(например, для потоков). Здесь массив разбивается на две примерно равные

части и каждая из них сортируется по отдельности. Затем два отсортированных подмассива сливаются в один.

8. 
   Пирамидальная сортировка - при этой сортировке сначала строится пирамида из элементов исходного массива. Пирамида (или двоичная куча) — это способ представления элементов, при котором от каждого узла может отходить не больше двух ответвлений. А значение в родительском узле должно быть больше значений в его двух дочерних узлах.
   

Пирамидальная сортировка похожа на сортировку выбором, где сначала нужно найти максимальный элемент, а затем поместить его в конец. Дальше нужно рекурсивно повторять ту же операцию для оставшихся элементов.

1.8. Другие алгоритмические инструменты.

1.8.1. Жадные приближенные алгоритмы

Жадный алгоритм (greedy algorithm) — это алгоритм, который на каждом шагу делает локально наилучший выбор в надежде, что итоговое решение будет оптимальным.

К примеру, алгоритм Дейкстры нахождения кратчайшего пути в графе вполне себе жадный, потому что на каждом шагу нужно искать вершину с наименьшим весом, в которой мы еще не бывали, после чего обновляем значения других вершин. При этом можно доказать, что кратчайшие пути, найденные в вершинах, являются оптимальными.

К слову, алгоритм Флойда, который тоже ищет кратчайшие пути в графе (правда, между всеми вершинами), не является примером жадного алгоритма. Флойд демонстрирует другой метод — метод динамического программирования.

17

1.8.2. Вероятностные алгоритмы

Вероятностный алгоритм — алгоритм, предусматривающий обращение на определённых этапах своей работы к генератору случайных чисел с целью получения экономии во времени работы за счёт замены абсолютной достоверности результата достоверностью с некоторой вероятностью.

Вероятностный алгоритм не гарантирует правильность результата. Однако мы можем получить вероятность ошибки настолько маленькую, что это почти гарантирует, что алгоритм вырабатывает правильный ответ. Сложность разрядной операции алгоритма может стать полиномиальной, при этом мы допускаем небольшой шанс для ошибок. Вероятностный алгоритм в этой категории возвращает результат либо простое число, либо составной объект, основываясь на следующих правилах:

a. Если целое число, которое будет проверено, — фактически простое число, алгоритм явно возвратит простое число.

b. Если целое число, которое будет проверено, — фактически составной объект, алгоритм возвращает составной объект с вероятностью 1 - ℇ, но может возвратить простое число с ℇ вероятности. Вероятность ошибки может быть улучшена, если мы выполняем алгоритм несколько раз с различными параметрами или с использованием различных методов. Если мы выполняем алгоритм m раз, вероятность ошибки может уменьшиться до _m.

1.9. Алгоритмы на графах.

1.9.1. Виды алгоритмов на графах.

1. 
   Поиск в глубину - из названия этого метода графа ясно, что в процессе поиска нужно идти «вглубь» графа настолько, насколько возможно. Следуя алгоритму, мы сможем последовательно обойти все вершины графа, которые
   

18



доступны из начальной вершины. Если ребро ведет в не пройдённую до этого момента вершину, то алгоритм запускается с нее. В случае если ребер, которые ведут в не рассмотренную вершину нет, то происходит возврат назад.

2. 
   Поиск в ширину - алгоритм позволяет найти кратчайший (содержащий наименьшее число ребер) путь из одной вершины графа до всех остальных вершин. В нем сначала посещаются все вершины, смежные с текущей, а затем их потомки.
   
3. 
   Топологическая сортировка - является упорядочиванием вершин бесконтурного ориентированного графа. Его цель состоит в том, чтобы перенумеровать вершины так, чтобы каждое ребро из вершины с меньшим номером вело в вершину с большим. Другими словами, нужно найти перестановку вершин, которая соответствует порядку, задаваемому всеми ребрами графа.
   
4. 
   Алгоритм Косарайю - для того чтобы найти компоненты сильной связности, сначала выполняется поиск в глубину, каждый раз выбирается не посещенная вершина с максимальным номером, который был получен при обратном проходе. Полученные деревья являются сильно связными компонентами.
   
5. 
   Алгоритм Тарьяна - Этот алгоритм в первую очередь представляет из себя один из вариантов поиска в глубину. Вершины посещаются от корней к листьям, а окончание их обработки происходит на обратном пути.
   

1.10. Оценка сложности.

Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000.

19

При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.

Допустим, некоторому алгоритму нужно выполнить 4n³ + 7n условных операций, чтобы обработать n элементов входных данных. При увеличении n на итоговое время работы будет значительно больше влиять возведение n в куб, чем умножение его на 4 или же прибавление 7n. Тогда говорят, что временная сложность этого алгоритма равна О(n³), т. е. зависит от размера входных данных кубически.

Использование заглавной буквы О (или так называемая О-нотация) пришло из математики, где её применяют для сравнения асимптотического поведения функций. Формально O(f(n)) означает, что время работы алгоритма (или объём занимаемой памяти) растёт в зависимости от объёма входных данных не быстрее, чем некоторая константа, умноженная на f(n).

1.10.1. Виды сложности.

1. 
   O(n) — линейная сложность
   

Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придётся пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.

2. O(log n) — логарифмическая сложность

Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нём какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отбросим вторую половину массива — там его точно нет. Если же меньше, то наоборот — отбросим начальную половину.

20

И так будем продолжать делить пополам, в итоге проверим log n элементов.

3. O(n²) — квадратичная сложность

Такую сложность имеет, например, алгоритм сортировки вставками. В канонической реализации он представляет из себя два вложенных цикла: один, чтобы проходить по всему массиву, а второй, чтобы находить место очередному элементу в уже отсортированной части. Таким образом, количество операций будет зависеть от размера массива как n * n, т. е. n².

Бывают и другие оценки по сложности, но все они основаны на том же принципе.

Также случается, что время работы алгоритма вообще не зависит от размера входных данных. Тогда сложность обозначают как O(1). Например, для определения значения третьего элемента массива не нужно ни запоминать элементы, ни проходить по ним сколько-то раз. Всегда нужно просто дождаться в потоке входных данных третий элемент и это будет результатом, на вычисление которого для любого количества данных нужно одно и то же время.

Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.

Глава 2. Практическая часть.

В своей курсовой работе я хочу рассмотреть и сравнить два вида сортировки это Сортировка пузырьком и Обычная сортировка:

1)Сортировка пузырьком (англ. bubble sort) — простой алгоритм сортировки. Для понимания и реализации этот алгоритм — простейший, но эффективен он лишь для небольших массивов.

21

Как было сказано выше, данный метод сортировки являетя простейшим и нет никаких особых проблем для его освоения. Ниже будет представлен код данной сортировки

#include

using namespace std;

int main() {

setlocale(LC_ALL, "rus");

int digitals[7]; // объявили массив на 10 ячеек

cout << "Введите 7 чисел для заполнения массива: " << endl;

for (int i = 0; i < 7; i++) {

cin >> digitals[i]; // "читаем" элементы в массив

}

for (int i = 0; i < 7; i++) {

for (int j = 0; j < 6; j++) {

if (digitals[j] > digitals[j + 1]) {

int b = digitals[j]; // создали дополнительную переменную

digitals[j] = digitals[j + 1]; // меняем местами

digitals[j + 1] = b; // значения элементов

}

}

}

cout << "Массив в отсортированном виде: ";

22

for (int i = 0; i < 7; i++) {

cout << digitals[i] << " "; // выводим элементы массива

}

system("pause");

return 0;

}

1. 
   Для начала мы объявляем массив на 7 элементов (int digitals[7];)
   
2. 
   Дальше начинается первый цикл в котором мы “читаем” элементы в данном масиве ( for (int i = 0; i < 7; i++)
   

cin >> digitals[i];)

3. 
   Начинается второй цикл в котором сначала мы сравниваем массив ( if (digitals[j] > digitals[j + 1]) ) и если он оказывается больше то происходит следующее:
   

• 
  Создаётся дополнительная переменная ( int b = digitals[j]; )
  
• 
  Массив ( digitals[j] ) меняется местами с массивом ( digitals[j + 1] )
  
• 
  Массив ( digitals[j + 1] ) приравнивается к значению ( b )
  

4. 
   В последнем цикле элементы от первого номера до седьмого выводятся элементы массива ( for (int i = 0; i < 7; i++)
   

cout << digitals[i] << " "; )

Принцип работы Сортировки пузырьком довольно таки прост, мы идём по массиву слева направо. Если текущий элемент массива больше следующего, то эти элементы меняются местами, так происходит до того момента, пока весь массив не будет отсортирован.

2)Простая сортировка – в этой сортировке все неупорядоченные элементы будут располагаться в упорядоченном порядке Сортировка данных является

23

очень важным моментом в программировании, т.к. абсолютно любой программист рано или поздно сталкивается с необходимостью сортировать какие-либо данные. Ниже код данной простенькой сортировки:

#include;

#include;

#include

using namespace std;

int main()

{

setlocale(LC_ALL, "Rus");

vector v = { 43,20,7,22,54 };

sort(v.begin(), v.end());



for (auto element : v)

cout << element << endl;

}

В данном программном коде мы должны подключить такую библиотеку как <algorithm> что бы использовать команду ( sort ). Далее в векторе мы должны указать массив из произвольных чисел в данном случае это ( { 43,20,7,22,54 }; ), затем использую команду ( sort ) отсортировать данный массив. В цикле мы используем команду ( auto ) что бы вывести отсортированный массив.

24

Заключение.

В данной курсовой работе были рассмотрены такие виды сортировки как:

Сортировка пузырьком и Обычная сортировка. Сортировка пузырьком – простой в реализации и малоэффективный алгоритм сортировки. Данный метод сортировки изучается одним из самых первых в теории, в то время когда на практике данный метод используется очень редко. Что бы отсортировать какое то большое количество информации, лучше не использовать данный метод.

Список литературы.

1. 
   Генри С. Уоррен — Алгоритмические трюки для программистов, 2-е издание
   
2. 
   Дасгупта С., Пападимитриу Х., Вазирани У. — Алгоритмы
   
3. 
   Дж. Макконелл — Анализ алгоритмов. Вводный курс, 2-е дополненное издание
   
4. 
   Бёрд Р. — Жемчужины проектирования алгоритмов. Функциональный подход
   
5. 
   Р. Лафоре — Структуры данных и алгоритмы в Java, 2-е издание
   
6. 
   Р. Седжвик, К. Уэйн — Алгоритмы на Java, 4-е издание
   
7. 
   Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн — Алгоритмы. Построение и анализ. Издание 3-е
   
8. 
   Т. Кормен — Алгоритмы. Вводный курс
   

25