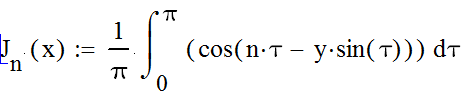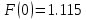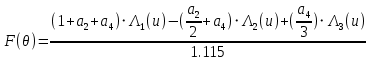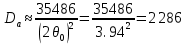|
|
ДВУХЗЕРКАЛЬНАЯ АНТЕННА ПО СХЕМЕ КАССЕРГЕНА. РРвАФУиСМС_ЖуковскийАС_БСМС1851. Курсовой проект двухзеркальная антенна по схеме кассергена студент 3 курса группа бсмс1851
МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ
КАФЕДРА ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
КУРСОВОй ПРОЕКТ
двухзеркальная антенна
по схеме кассергена
Выполнил:
студент
3 курса
группа БСМС1851
Жуковский Артемий Сергеевич
Вариант 07
Научный руководитель:
Доцент Смирнов Е. В.
МОСКВА 2021 г
содержание
введение
Зеркальные антенны являются наиболее распространёнными узконаправленными антеннами. Их широко примененяют благодаря простоте их конструкции, возможности получения разнообразных видов диаграмм направленности (ДН), а также высокому коэффициенту полезного действия (КПД). В радиолокационных применениях зеркальные антенны позволяют легко получить равносигнальную зону, допускают одновременное формирование нескольких диаграмм направленности общим зеркалом (в том числе суммарных и разностных). Некоторые типы зеркальных антенн могут обеспечивать достаточно быстрое качание луча в значительном угловом секторе. Зеркальные антенны являются наиболее распространённым типом антенн в космической связи и радиоастрономии, и именно с помощью зеркальных антенн удаётся создавать гигантские антенные сооружения с эффективной поверхностью раскрыва, измеряемой тысячами квадратных метров.
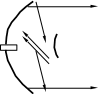
Рис. 1. Идея конструкции двухзеркальной антенны.
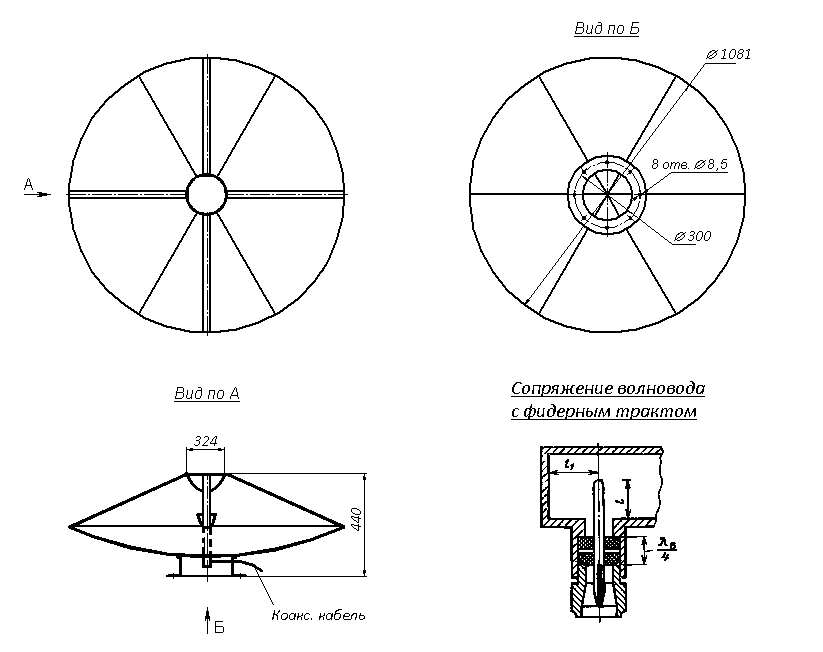
Двухзеркальня антенна по схеме Кассегрена представляет собой систему состоящую из двух отражающих поверхностей – софокусных параболоида и гиперболоида – и облучателя, установленного во втором фокусе гиперболоида. Все расстояния по ломаной линии от фокуса до раскрыва одинаковы, что обеспечивает синфазность поля в раскрыве. Двухзеркальная антенна является более компактной, чем однозеркальная, и обеспечивает более равномерное распределение возбуждения по раскрыву, а также является более помехозащищённой, даёт возможность укоротить тракт СВЧ и разместить основную часть конструкции облучателя за зеркалом, что особенно удобно в моноимпульсных радиолокаторах. При оптимизации размеров облучателя и малого зеркала удаётся получить высокий коэффициент использования поверхности (КИП)νисп = 0,650,7. Недостаток системы – затенение её раскрыва малым зеркалом, а также обратная реакция малого зеркала на облучатель.
Принцип работы двухзеркальной антенны по схеме Кассегрена состоит в том, что электромагнитное поле от облучателя, отражаясь от второго зеркала (гиперболоида) попадает на поверхность первого зеркала (параболоида), а отражённое от него, наконец, излучается в пространство, причём вид излучаемого в простанство поля совпадает с полем излучаемым плоской синфазной поверхностью.
исходные данные и задание на проектирование
Спроектировать двухзеркальную антенну Кассергена. Антенна устанавливается на борту искусственного спутника Земли (ИСЗ) и осуществляет передачу на Землю линейно поляризованных сигналов на частоте f0. ИСЗ находится на стационарной орбите и предназначен для ретрансляции телевизионных сигналов на радиолинии Земля-ИСЗ-Земля.
Исходные данные:
Частота f0, ГГц6
Мощность бортового передатчика Pпер, Вт 50
Коэффициент усиления приемной антенны на ЗемлеGпр, дБ50
Мощность на входе наземного приемникаPвх.пр, Вт 1·10–10
Потери в фидерных трактах радиопередающей антенны αпер, дБ 0,5
Потери в фидерных трактах приемной антенны αпр, дБ 0,5
Потери в атмосфере Земли αпр, дБ 0
Протяженность радиолинии ИСЗ-Земля r, км 40000
ЭНЕРГЕТИКА РАДИОЛИНИИ ИСЗ-ЗЕМЛЯ
На линии ИСЗ-Земля передача информации ведется непосредственно из пункта передачи в пункт приема, т.е. используется линия передачи I типа. Для этой линии мощность на входе приемника в условиях свободного пространства выражается соотношением:
Pвх.пр = PперηперGперGпрηпрλ2/(4πr2)
КПД фидерного тракта со стороны передатчика и приемника выражаются через соответствующие потери формулами:
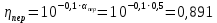 (2) (2)
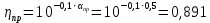 (3) (3)
Длина волны на заданной частоте f0 равна:
λ = с / f0 = 3·108 / 6·109 = 0,05 м
(c – скорость света в вакууме и атмосфере, коэффициент преломления будем считать равным 1).
Выразим коэффициент усиления приемной антенны на Земле в абсолютных единицах:
Gпр = 100,1·50 = 100000.
Тогда можно получить выражение для коэффициента усиления у бортовой передающей антенны:
Pвх.пр = PперηперGперGпрηпрλ2/(4πr2)
Gпер = 4πr2Pвх.пр/(Pпер(1)ηпер(1)Gпр(2)ηпр(2)λ2) =
= 4π·(4·107)2·1·10–10/(50·0,891·100000·0,891·0,052) ≈ 2026
или в логарифмической форме:
Gпер = 10 lg (2026) = 33,07 дБ.
Положим КПД антенны равным ηа = 0,87, тогда коэффициент направленного действия (КНД) Dантенны может быть определен из формулы:
Dа = G / ηа = 203 / 0,87 ≈ 2329
или в логарифмической форме:
Dа = 10 lg (232,9) = 33,67дБ.
Расчет размера рефлекторов, фокусных расстояний, угловых размеров
Перед началом расчётов основных конструктивных параметров зеркал двух зеркальной антенны по схеме Кассегрена рассмотрим рис.2, на котором показаны основные параметры зеркал.
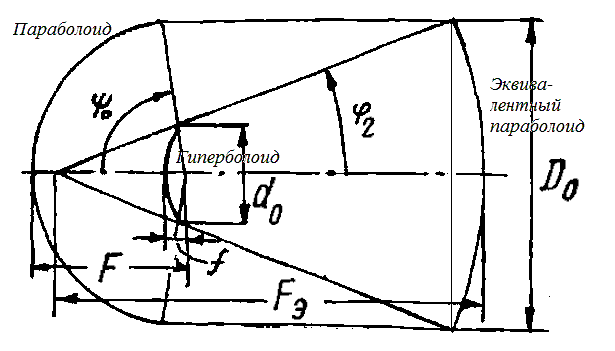
Рис. 2. Эквивалентный параболоид.
На рис.2: e – эксцентриситет гиперболического зеркала; 0 – половина угла раскрыва большого зеркала (или угла раскрыва эквивалентного параболоида); 2 – половина угла зрения на малое зеркало (); F – фокусное расстояние большого зеркала; f – фокусное расстояние малого зеркала (гиперболоида); FЭ – фокусное расстояние эквивалентного параболоида; D0 – диаметр раскрыва большого зеркала; d0 – диаметр раскрыва малого зеркала.
Диаметр раскрыва большого зеркала определяем из соотношения (8.15) [1], принимая в качестве оценочного значения КИП νисп = 0,7 , где S– площадь раскрыва:
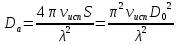 , откуда , откуда
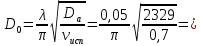 0,918 м 0,918 м
Диаметр вспомогательного зеркала выбираем, в соответствии с рекомендациями в методических указаниях на курсовую, из соотношения d0 = (0,06÷0,2) D0, примем
d0= 0,19·D0 = 0,174 м
Обычно эксцентриситет лежит в пределах e = (1,2÷2). Примем ориентировочное значение
e = 1,25.
Для определения конструктивных параметров антенны воспользуемся соотношением из методических указаний к курсовой. Фокусное расстояние большого зеркала:
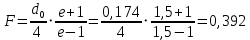 м м
Из формулы
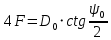
находим:
ψ0 = 2 arcctg (4F / D0) = 60,64°
Эксцентриситет гиперболического зеркала определяется соотношением:
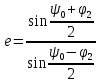
Тогда можно численно определить 2 – угол облучения краев малого зеркала:
2 = 7,435°
Фокусное расстояние малого зеркала:
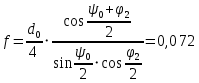 м м
Расстояние между фокусами гиперболоида:
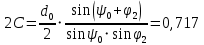 м м
Расчёт облучателя
В качестве облучателя проектируемой антенны будем использовать прямоугольный рупор. Его конструкция показана на рис. 3.
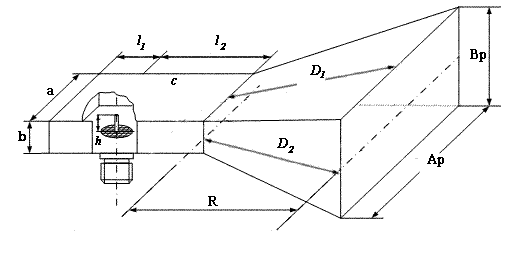
Рис. 3. Прямоугольный рупор.
Рассчитаем параметры прямоугольного рупора:
Размеры сечения (a и b) прямоугольного волновода выбирается из условия распространения только одного основного типа волны H10
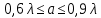 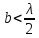
Выбираем стандартный волновод по Таблице 17.14 из справочника Р. Г. Варламова [5]. Нам подходит R58 размерами a = 40,39 мм и b = 20,193 мм, т.е. a = 40,39·10–3 м и b = 20,193·10–3 м
Проверка выполнения условия распространения волны H10 :
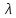 = 50·10–3 м , = 50·10–3 м , 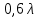 = 30·10–3 м = 30·10–3 м 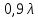 = 45·10–3 м = 45·10–3 м
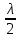 = 25·10–3 м = 25·10–3 м
Для a: 30·10–3 м 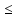 40·39–3 м 40·39–3 м 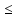 45·10–3 м 45·10–3 м
т.е. условие 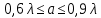 выполняется. выполняется.
Для b:
20,193·10–3 м 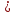 25·10–3 м 25·10–3 м
т.е. условие 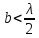 выполняется. выполняется.
Критическая длина волны для волны H10:
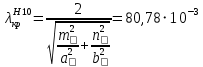 м м
Длина волны в волноводе:
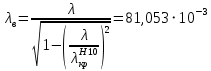 м м
Длина отрезка волновода l1 от возбуждающего штыря до закорачивающей стенки выбирается из условия согласования с питающей коаксиальной линией:
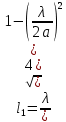 м м
Длина волновода l2 от возбуждающего устройства до горловины рупора выбирается из условия фильтрации высших типов волн. Вблизи штыря кроме волны H10 возбуждается множество высших типов волн, все они оказываются в за критическом режиме, и по мере движения к рупору затухают по экспоненте. Высшие типы волн не должны проходить в горловину рупора, а затем в его раскрыв, для этого их амплитуда должна уменьшиться на длине l2 примерно в 100 раз. Ближайшей к основной высшей волной в таком возбуждающем устройстве является волна H20. Для уменьшения её амплитуды в 100 раз, величину l2 выражаем из уравнения:
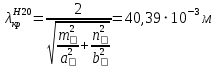
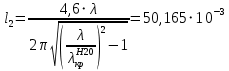 м м
Для нахождения размеров раскрыва прямоугольного рупора, необходимых для получения диаграммы направленности шириной 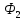 , воспользуемся формулами (6.7 6.8) [4]: , воспользуемся формулами (6.7 6.8) [4]:
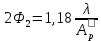 - в плоскости вектора H - в плоскости вектора H
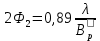 - в плоскости вектора E - в плоскости вектора E
Следовательно, размеры раскрыва прямоугольного рупора:
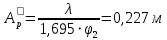
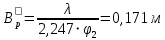
Где значение 2 нужно подставлять в радианах (2 = 7,435° = 0,1298 рад)
Определения длины рупора:
Для пирамидального рупора длины рупора в плоскости вектора H и в плоскости вектора Е формуле 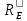 и и 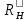 могут быть различными. В нашем случае так и есть, следовательно рупор - клиновидный. Потому для получения в итоге оптимального рупора т.е. рупора, который при заданной длине имеет максимальный КНД, берём наибольшее значение. В нашем случае, наибольшее значение имеет длина рупора в плоскости вектора Н. Фазовые искажения в раскрыве рупора при расчёте таким методом не будут превышать допустимых ( могут быть различными. В нашем случае так и есть, следовательно рупор - клиновидный. Потому для получения в итоге оптимального рупора т.е. рупора, который при заданной длине имеет максимальный КНД, берём наибольшее значение. В нашем случае, наибольшее значение имеет длина рупора в плоскости вектора Н. Фазовые искажения в раскрыве рупора при расчёте таким методом не будут превышать допустимых (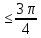 ), чтобы не оказывать значительного негативного влияния на КНД рупора. ), чтобы не оказывать значительного негативного влияния на КНД рупора.
Определим длину рупора сперва в плоскости вектора H по формуле (6.13) [4]
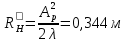
После определим длину рупора в плоскости вектора E по отношению длин рупора в плоскостях векторов E и H к размерам раскрыва и размерам питающего волновода из формулы (6.16) [4]
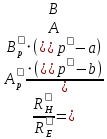 Следовательно Следовательно 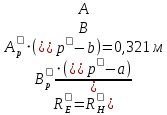
В итоге длина рупора получается R = 0,344 м
Расчёт возбуждающего устройства
В данной антенне схема возбуждения представляет собой волноводно-коаксиальный переход, при котором штыревой вибратор возбуждает прямоугольный волновод.
Критерием согласования возбуждающего устройства с волноводом служит режим бегущей волны в коаксиальном питающем фидере, т.е. равенство входного сопротивления Rвх возбуждающего устройства волновому сопротивлению фидера ф (для коаксиального кабеля 50 Ом). Согласно (6.18) [4], для прямоугольного волновода с расположением возбуждающего штыря в середине широкой стенки:
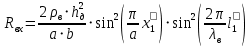
Где 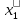 - положение штыря на широкой стенке волновода, в нашем случае по середине, следовательно - положение штыря на широкой стенке волновода, в нашем случае по середине, следовательно 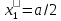
Используем эту формулу в дальнейшем для проверки верности расчётов.
А пока расчитаем требуемые параметры:
Расчитаем волновое сопротивление волновода:
в=120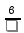 = 611 Ом = 611 Ом
l1– длина отрезка волновода от возбуждающего штыря до закорачивающей стенки. Была рассчитана выше. Равняется 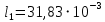 м м
l – геометрическая длина штыря, подбираем значение так, чтобы итоговое сопротивление возбуждающего устройство максимально приблизилось к сопротивлению фидера (50 Ом)
l = 0,0362 м
hд – действующая высота штыря в волноводе, находим ее по формуле (6.21) [4]
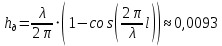 м м
Проверяем согласование: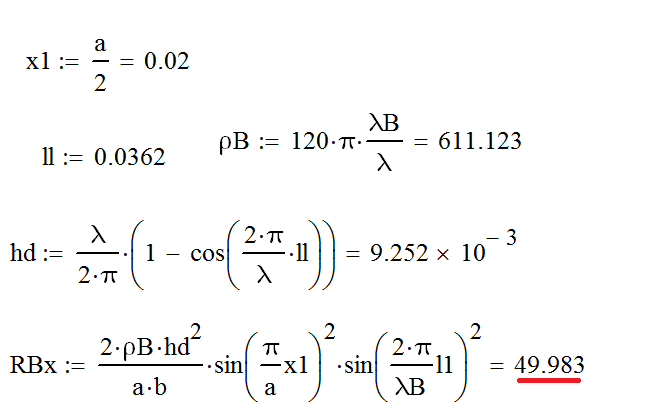
Получаем входное сопротивление питающего устройства на 0,017 Ом расходящееся с сопротивлением фидера, что гарантирует хорошее согласование и незначительные потери на переходе фидер-волновод.
Сначала рассчитаем диаграмму направленности прямоугольного рупора в плоскостях Е и Н по формулам Кирхгофа (6.30)-(6.31) [4]:
- в плоскости H
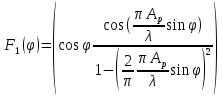
- в плоскости E
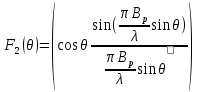
Результаты расчета поля в раскрыве зеркала по данным формулам в программе Mathcad 15 представлены на рис. 4.
Диаграмма направленности рупора по половинному уровню напряжённости поля (-3 дБ или -0.707) имеет ширину 15, угол на малое зеркало от облучателя равен 22 = 14,87°. Таким образом, диаграмма направленности облучателя получилась подходящей для эффективного облучения малого зеркала системы.
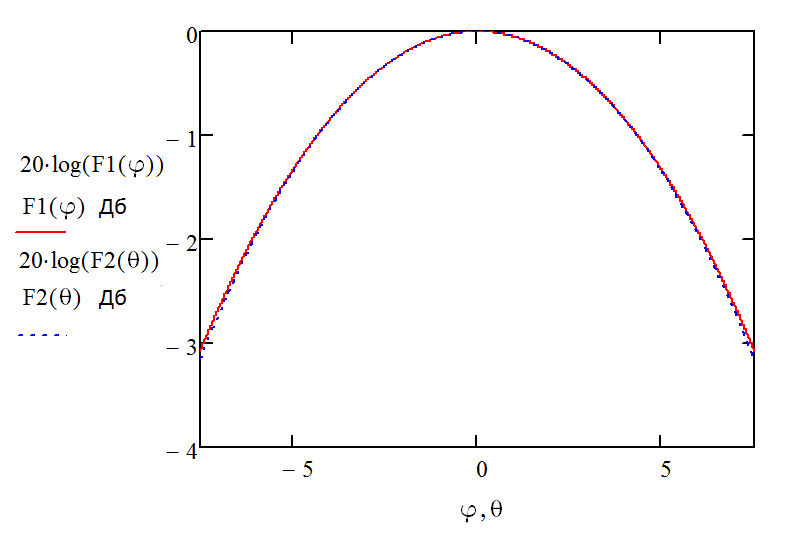
Рис. 4. Диаграмма направленности конического рупора в плоскостях Н и Е.
Для расчета диаграммы направленности антенны исходную двухзеркальную антенну заменим эквивалентной однозеркальной антенны, определим распределение амплитуд поля по раскрыву этого эквивалентного зеркала, и по нему рассчитаем форму диаграммы направленности антенны. Диаметр эквивалентного зеркала равен диаметру большого зеркала двухзеркальной антенны, а фокусное расстояние равно:
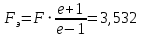 м м
По известной нормированной диаграмме направленности облучателя определяется поле в раскрыве параболоида F(). При этом считается, что фазовый центр облучателя (точка, из которой распространяются сферические волны) совмещен с фокусом параболоида, а параболоид находится от облучателя на расстоянии, соответствующем дальней зоне. Как известно, в сферической волне амплитуда напряженности поля убывает обратно пропорционально расстоянию, поэтому на пути от фокуса до поверхности зеркала (расстояние от фокуса до разных точек параболоида различное) произойдет изменение амплитудных соотношений в соответствии с изменением ( возрастает по мере движения точки от центра зеркала к его периферии). После отражения от поверхности зеркала пучок лучей принимается за параллельный, а волна за плоскую. По этой причине можно считать, что амплитудные соотношения поля на поверхности зеркала соответствуют амплитудным соотношениям на раскрыве. Кроме того, равенство путей, проходимых любым лучом от фокуса до поверхности раскрыва, позволяет утверждать, что поле на раскрыве будет синфазным.
Дальнейший расчет проведем для функции F1(φ).
Амплитуда напряженности поля в произвольной точке раскрыва в нормированном представлении:
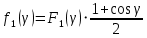 (31) (31)
где γ – угол между направлением из фокуса на данную точку и фокальной осью зеркала.
Перейдем от функции f1(γ) к функции относительного переменного радиуса раскрыва f1(ρ/R0) и аппроксимируем ее полиномом 4 степени:
f(ρ/R0) = 1 + a2(ρ/R0)2 + a4(ρ/R0)4
Для нахождения коэффициентов a2 и a4 выберем две точки, например, x = 0,15 и x = 0,4, приравняем в них f1(x) и f(x) и решим систему из двух уравнений с двумя неизвестными, относительно a2 и a4, методом обратной матрицы. Решение в Mathcad и сравнение графика аппроксимации напряжённости поля с его реальным графиком показано на рис.5.

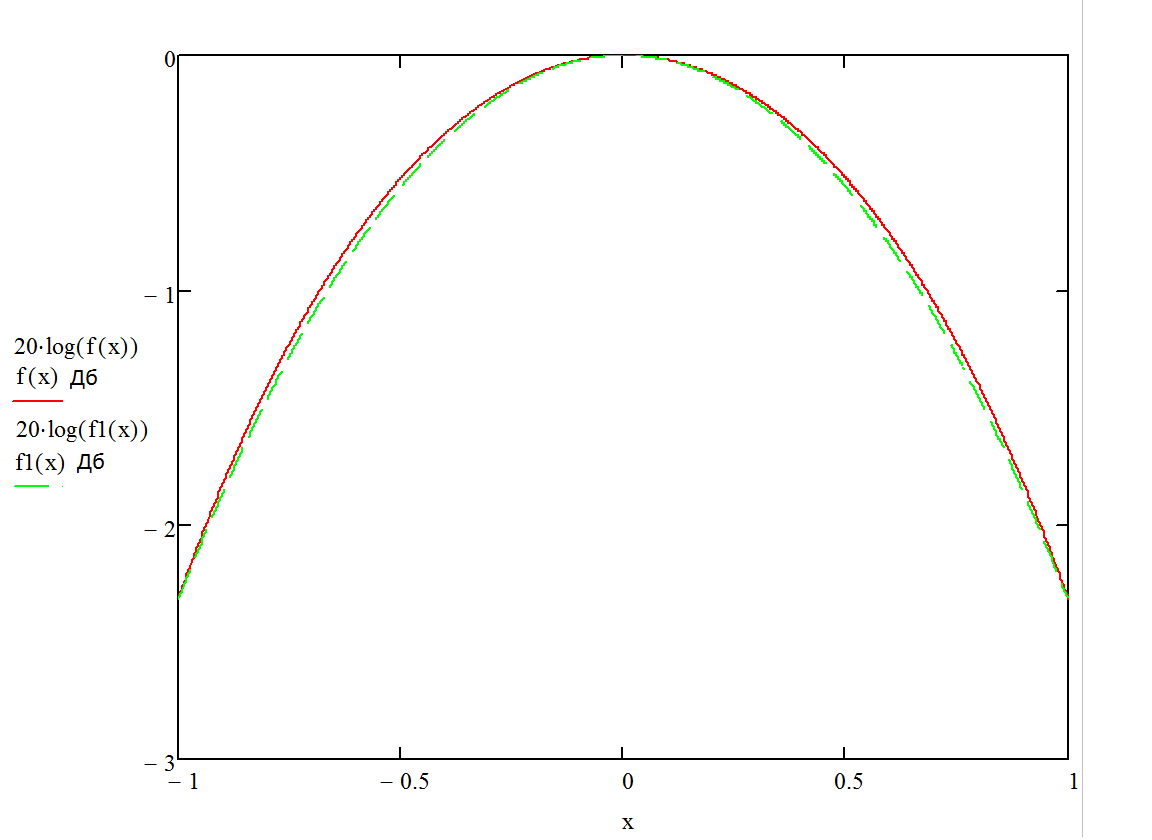
Рис. 5. Определение коэффициентов a2 и a4.
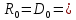 0,918 м 0,918 м
Поскольку график аппроксимации близок к графику реального распределения поля, можно считать диаграмму направленности следующей:
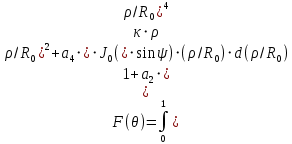
После интегрирования получаем:
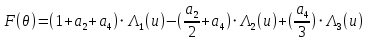
где 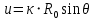
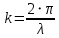 - волновое число - волновое число
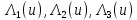 - лямбда – функции на основе функций Бесселя 1-го, 2го и 3го порядков: - лямбда – функции на основе функций Бесселя 1-го, 2го и 3го порядков:
.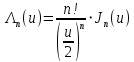 (6.39) [4] (6.39) [4]
Функция Бесселя n-го порядка:
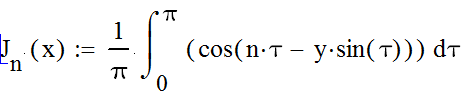
После расчёта был выявлен максимум функции ДН 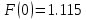
Для построения нормированной ДН используем функцию:
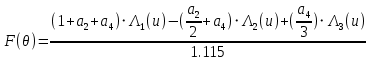
График нормированной ДН антенны показан на рис. 6, а со шкалой в ДБ - на рис. 7.
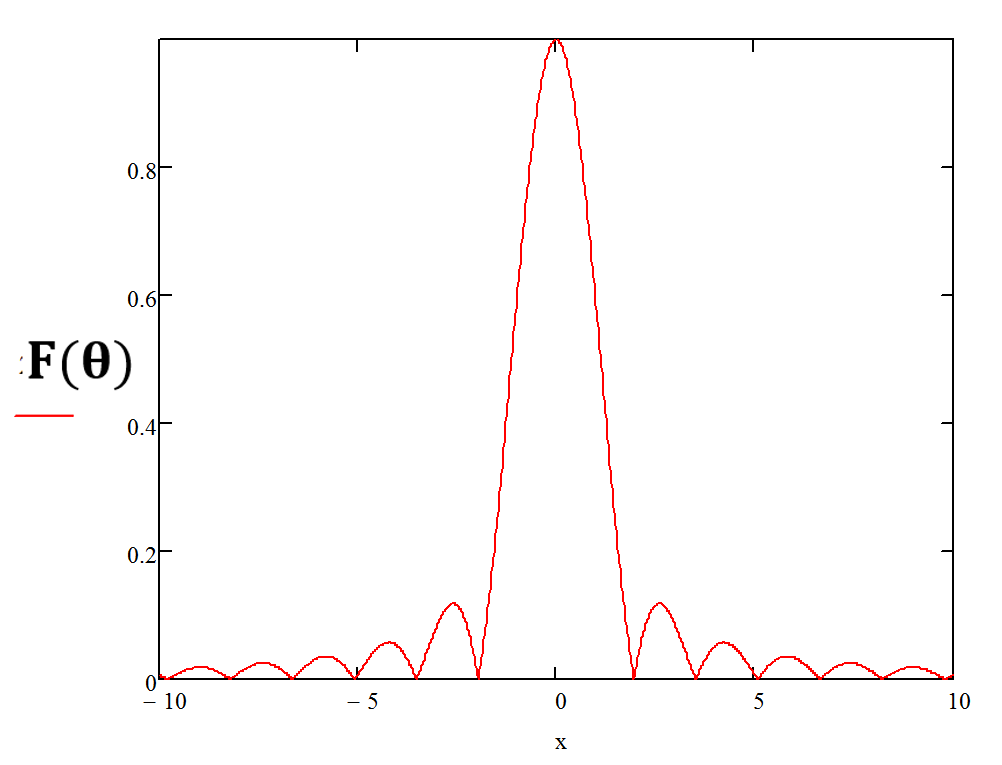
Рис. 6. Диаграмма направленности антенны +-10 градусов.
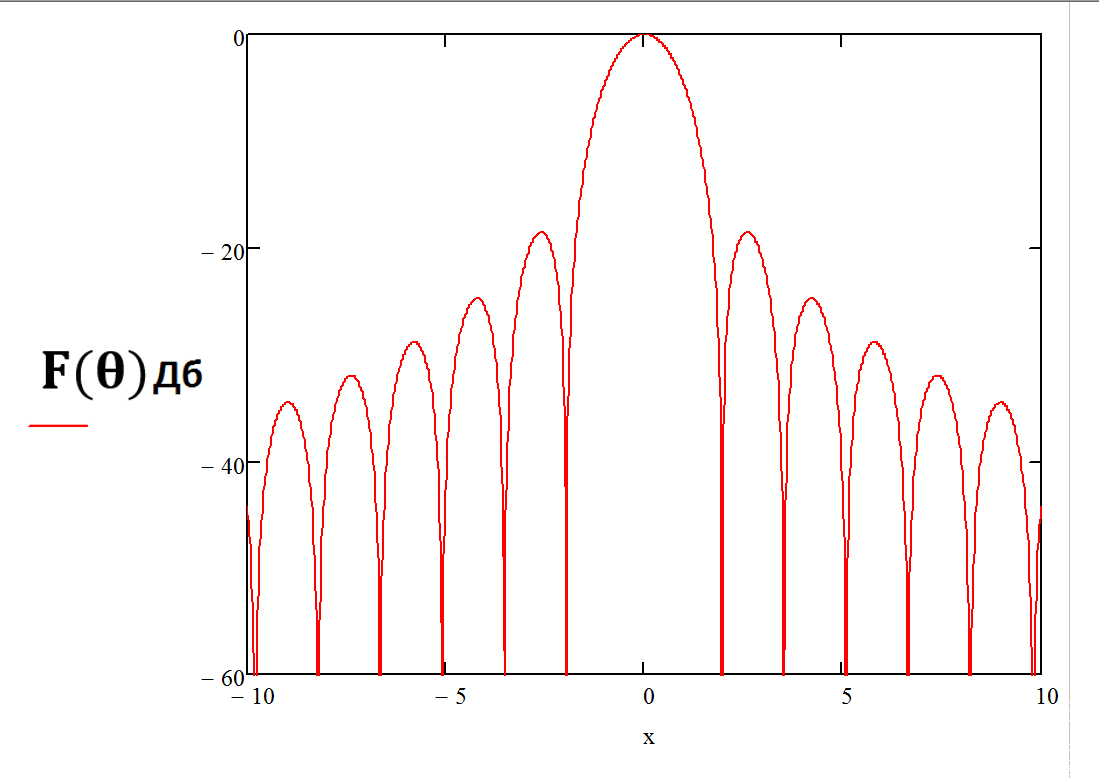
Рис. 7. Диаграмма направленности антенны +-10 градусов в децибелах.
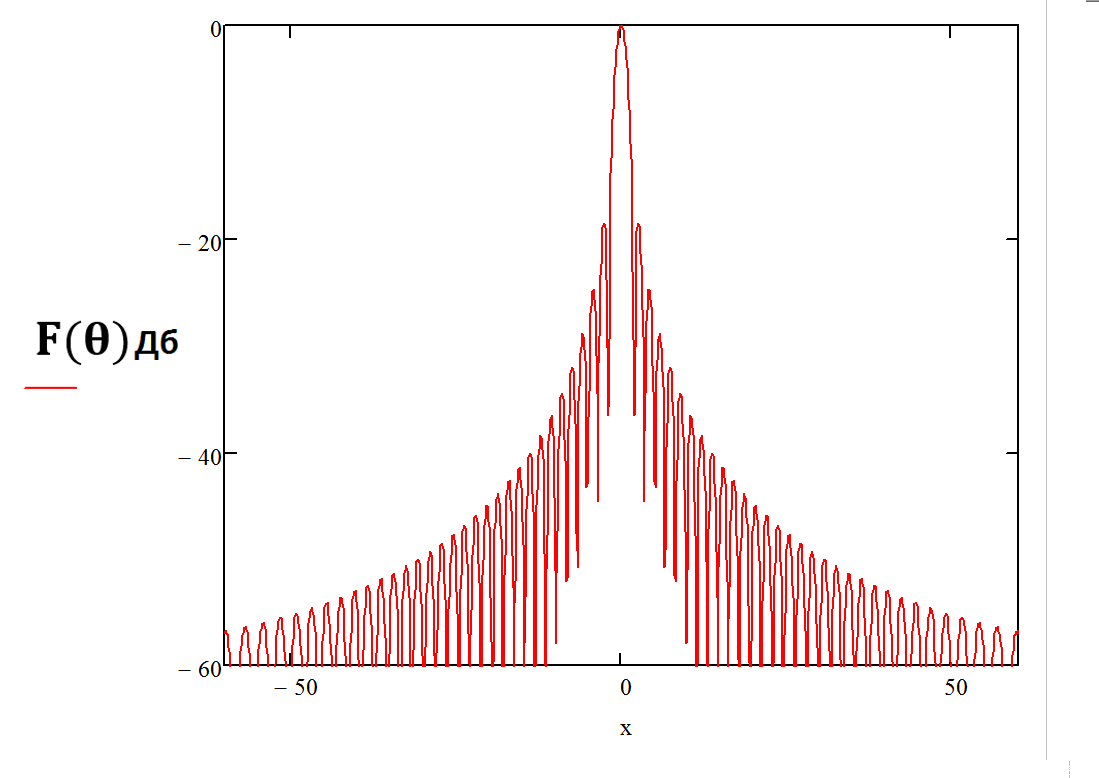
Рис. 8. Диаграмма направленности антенны +-60 градусов в децибелах
По графику рис. 6 определяем:
- уровень первого бокового лепестка F(θ*) = 0,119= -18.5 Дб;
- ширина главного лепестка 2θ0,5 = 2.26°; 2θ0 = 3.94°.
Коэффициент направленного действия антенны приблизительно рассчитаем по ширине главного лепестка, приняв энергию главного лепестка за 87%:
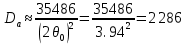
В начале расчетов мы принимали КНД равным Dа(оцен.) = 2329 при оценочном КИП раскрыва νисп(оцен.) = 0,7. Таким образом, с учетом реального значения Dа, результирующий КИП раскрыва равен:
νисп = νисп(оцен.)*Dа / Dа(оцен.) = 0,7*2286 / 2329 = 0,687
ЛИТЕРАТУРА
Ерохин Г.А. и др. Антенно-фидерные устройства и распространение радиоволн. – М.: Горячая линия-Телеком, 2007.
Методические указания и задания на курсовой проект по курсу: «Распространение радиоволн и антенно-фидерные устройства в системах радиосвязи и радиодоступа» для студентов-заочников 3 курса (направление 210700, профиль: Системы радиосвязи и радиодоступа). Сост.: В. И. Корнюхин, В. Г. Кочержевский, В. М. Седов. –
М.: МТУСИ, 2013.
Айзенберг Г. З. и др. Антенны УКВ / Под ред. Г. З. Айзенберга. В 2-х ч. Ч.2. – М.: Связь, 1977.
Антенны и устройства СВЧ / Под ред. Д. И. Воскресенского. – М.: Сов. радио, 1972.
Краткий справочник конструктора радиоэлектронной аппаратуры. Под ред. Р. Г. Варламова. – М.: Сов. радио, 1972.
Методические указания по проектированию двухзеркальных антенн / Г. В. Кравцова / МЭИС. – М., 1982.
Гольдштейн Л.Д., Зернов Н.В. Электромагнитные поля и волны. –
М.: Сов. радио, 1971.
Кочержевский Г. Н. Антенно-фидерные устройства. – М.: Связь, 1972.
https://www.bsuir.by/m/12_100229_1_85506.pdf Белорусский государственный университет информатики и радиоэлектроники – «Исследование прямоугольного волновода и элементов на его основе.»
Драбкин А.Л., Лузенко В.Л., Кислов А.Г. Антенно-фидерные устройства. Изд. 2-е, доп. и перераб.- М.: Сов. радио, 1974
Приложение
 |
|
|
 Скачать 277.55 Kb.
Скачать 277.55 Kb.

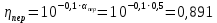 (2)
(2)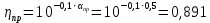 (3)
(3)
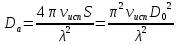 , откуда
, откуда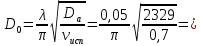 0,918 м
0,918 м 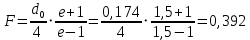 м
м 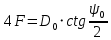
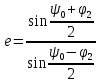
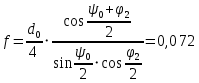 м
м 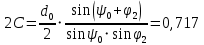 м
м 
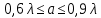
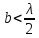
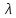 = 50·10–3 м ,
= 50·10–3 м , 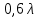 = 30·10–3 м
= 30·10–3 м 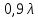 = 45·10–3 м
= 45·10–3 м 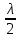 = 25·10–3 м
= 25·10–3 м 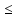 40·39–3 м
40·39–3 м 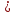 25·10–3 м
25·10–3 м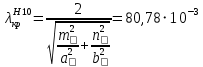 м
м 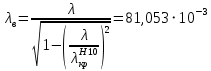 м
м 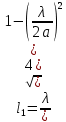 м
м 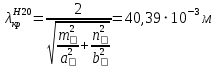
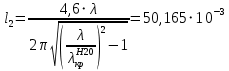 м
м 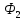 , воспользуемся формулами (6.7 6.8) [4]:
, воспользуемся формулами (6.7 6.8) [4]: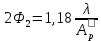 - в плоскости вектора H
- в плоскости вектора H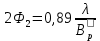 - в плоскости вектора E
- в плоскости вектора E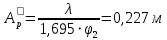
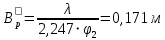
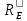 и
и 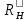 могут быть различными. В нашем случае так и есть, следовательно рупор - клиновидный. Потому для получения в итоге оптимального рупора т.е. рупора, который при заданной длине имеет максимальный КНД, берём наибольшее значение. В нашем случае, наибольшее значение имеет длина рупора в плоскости вектора Н. Фазовые искажения в раскрыве рупора при расчёте таким методом не будут превышать допустимых (
могут быть различными. В нашем случае так и есть, следовательно рупор - клиновидный. Потому для получения в итоге оптимального рупора т.е. рупора, который при заданной длине имеет максимальный КНД, берём наибольшее значение. В нашем случае, наибольшее значение имеет длина рупора в плоскости вектора Н. Фазовые искажения в раскрыве рупора при расчёте таким методом не будут превышать допустимых (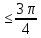 ), чтобы не оказывать значительного негативного влияния на КНД рупора.
), чтобы не оказывать значительного негативного влияния на КНД рупора.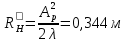
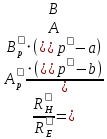 Следовательно
Следовательно 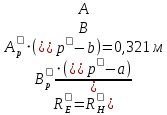
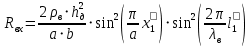
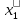
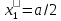
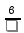
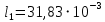
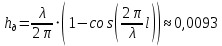
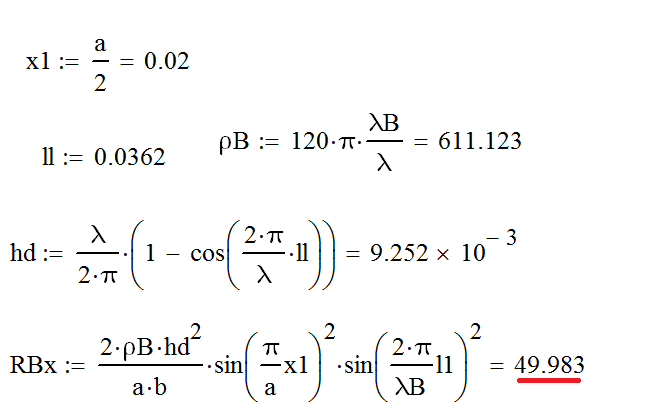
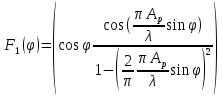
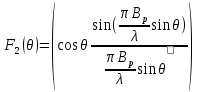

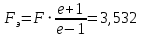 м
м 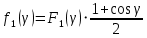 (31)
(31)

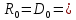 0,918 м
0,918 м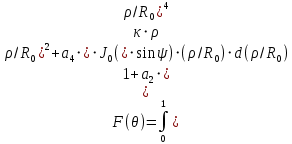
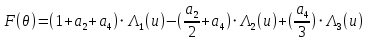
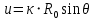
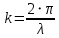 - волновое число
- волновое число 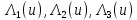 - лямбда – функции на основе функций Бесселя 1-го, 2го и 3го порядков:
- лямбда – функции на основе функций Бесселя 1-го, 2го и 3го порядков: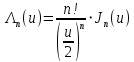 (6.39) [4]
(6.39) [4]