Математическое моделирование процессов чрезвычайных ситуаций. Курсовая матмод. Курсовой проект по дисциплине Математическое моделирование процессов чрезвычайных ситуаций Тема проекта
 Скачать 2.63 Mb. Скачать 2.63 Mb.
|
 Министерство науки и высшего образования Российской Федерации федеральное государственное автономное образовательное учреждение высшего образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Инженерная школа неразрушающего контроля и безопасности Направление подготовки 20.03.01 «Техносферная безопасность» Отделение контроля и диагностики КУРСОВОЙ ПРОЕКТ по дисциплине: Математическое моделирование процессов чрезвычайных ситуаций
Студент
Руководитель
Томск – 2022  Министерство науки и высшего образования Российской Федерации федеральное государственное автономное образовательное учреждение высшего образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Школа неразрушающего контроля и безопасности Направление подготовки 20.03.01 «Техносферная безопасность» Отделение контроля и диагностики ЗАДАНИЕ на выполнение курсового проекта Студенту:
Тема проекта:
ЗАДАНИЕ:
Задание выдал руководитель:
Задание принял к исполнению студент: Введение На предприятиях вода активно используется в производственных процессах, как в качестве химического вещества для протекания определенных реакций, так и как элемент системы охлаждения или очистки. Поэтому многие заводы и фабрики строятся на берегах рек для забора необходимого объема воды из них. Если на производстве организована система последовательного водоснабжения, то после очистки и охлаждения отработанной жидкости она снова используется. Но это требует дополнительных затрат на оборудование и расходные фильтрующие материалы. В большинстве случаев с целью экономии на предприятии работает система прямоточного водоснабжения, когда после однократного участия в технологическом процессе вода сбрасывается в тот же водоем, откуда она была ранее получена, что ведет к загрязнению. Все это приводит к невозможности её использования в будущем. Чтобы решить эти проблемы, необходимо знать и понимать, как будет распространяться загрязнение в водной среде. Математическое моделирование процесса загрязнения является решением этой проблемы. Цели работы: Изучение метода математического моделирования для применения в описании процессов чрезвычайных ситуаций Задачи: Познакомиться с литературными данными по данной работе Создать программу в среде MATLAB Произвести численные расчеты 1 Основная часть 1.1 Загрязнение водной среды Загрязнение водной среды – это актуальная проблема современности. В загрязнении учувствуют как предприятия, так и могут произойти различные аварии судов или загрязнение сведётся путем природных источников. Сточные воды — любые воды и атмосферные осадки, отводимые в водоёмы с территорий промышленных предприятий и населённых мест через систему канализации или самотёком, свойства которых оказались ухудшенными в результате деятельности человека. Промышленные отходы. В одних случаях стоки с производственных предприятий попадают в водоемы из-за пренебрежения очистными сооружениями. В других случаях утечки загрязненной воды происходят из-за поломок и аварий. Сельскохозяйственные предприятия. Современное земледелие не может обойтись без удобрений и пестицидов. Осадки смывают химические вещества в водоемы и грунтовые воды. Животноводство вносит свою лепту: дожди и паводки способствуют попаданию экскрементов в пресные водоемы. Даже небольшое количество навозосодержащей жидкости вызывает мор рыбы в реках и озерах. Попадают в водоемы и антибиотики, дезинфицирующе средства, стимуляторы роста, которые применяют в животноводстве. Утечки нефти. Небольшое количество нефтепродуктов содержится в стоках дорог и ливневой канализации. На судоходных реках случаются разливы нефти из танкеров. Нефтяные пятна крайне опасны для речной фауны. Твердые отходы. В водоемы попадет огромное количество мусора. Часть приносит ветром, часть несознательные граждане выбрасывают прямо в воду. В Азии есть реки, сплошь покрытые слоем плавучих отходов. Тепловое загрязнение. В озера и реки сливают воду из систем охлаждения тепловых и атомных станций и даже серверных центров. Такая вода не содержит повышенных концентраций загрязняющих веществ. Для экосистемы водоема губительна температура стоков: водоросли разрастаются сверх меры, а животные погибают. Атмосферные загрязнения. Пепел, сажа вредные атмосферные примеси также попадают в водоемы. Загрязнения воздуха при реакции с водой приводят к кислотным дождям. Природные источники загрязнений. Вулканический пепел, трупы животных, гниющие остатки растений, подмывание берегов. В поймах рек встречаются залежи ртути, свинца и других опасных веществ. Экологические проблемы, связанные с загрязнением воды: Ухудшение здоровья людей. Высокая концентрация опасных веществ приводит к онкологическим, дерматологическим заболеваниям, кишечным инфекциям. Опасно употреблять в пищу рыбу из грязных водоемов. Нарушение экосистем водоемов. В условиях избытка органики и удобрений водная флора активно растет, а рыба гибнет. Засорение водоемов порой приводит к гибели птиц. Реки несут мусор и растворенные опасные вещества в моря, что приводит к загрязнению Мирового океана. 1.2 Пути решения проблемы загрязнения воды Основной источник загрязнения вод – деятельность человека. Пути решения проблемы лежат в области очистки стоков, недопущения попадания загрязняющих веществ в водоемы и грунт. Чтобы полностью решить проблему загрязнения водных объектов, нужно применять комплексный подход. Играет роль и работа над сокращениями вредных выбросов в атмосферу, и личная культура водопользования. Поскольку проблема глобальная, необходимы совместные усилия всех стран. 1.2.1 Очистка промышленных и бытовых сточных вод Загрязненные стоки промышленных предприятий попадают в реки. В водоемы ведут канализационные коллекторы. Не везде применяют полноценную очистку сточных вод. Органические остатки менее опасны для природы, чем химические вещества. Но биологические сбросы представляют опасность для городов, расположенных ниже по течению реки. Во избежание загрязнения водоемов стоками разрабатывают и внедряют новые технологии очистки. Очистные сооружения называют «станции аэрации», хотя аэрация на них – далеко не единственный процесс. Этапы очищения стоков: Механическая очистка. Стоки проходят через решетки, песколовки, жироловки, первичные отстойники, фильтры и септики. Биологическая очистка. Активный ил, представляющий собой комбинацию бактерий и простейших, удаляет органические включения. Физико-химический этап. Нужен для удаления растворенных веществ и взвешенных частиц. Включает аэрацию, флотацию, центрифугирование и другие методы. Дезинфекция очищенных стоков. Для обеззараживания применяют ультрафиолетовое облучение, озонирование, обработку хлором и его соединениями. 1.2.2 Обеззараживание сточных вод с помощью химических реактивов Популярный способ уничтожить нежелательные микроорганизмы – добавление в воду реагентов-окислителей. С этой целью часто применяются хлор, диоксид хлора, озон, гипохлорит натрия. Недостаточное количество реагента не окажет желаемого эффекта, а избыточное навредит здоровью. Некоторые из обеззараживающих веществ уменьшают содержание солей металлов: окислитель реагирует с примесями, вследствие чего они выпадают в осадок в виде хлопьев. Точно рассчитанное количество реактивов убивает даже те бактерии, которые попадают в воду после обеззараживания. 1.2.3 Откачка загрязнённых вод в специальные резервуары Для откачки сильнозагрязненной воды применяют поверхностные и глубинные дренажные насосы. Откачивают жидкость в таких случаях: При прорывах канализационных труб; Удаление воды из подвалов и погребов; Очистка загрязненных водоемов; Осушение луж после дождей, паводков и прорывов труб; Откачка выгребных ям. Опасные жидкости, которые невозможно очистить, хранят в резервуарах. К таким жидкостям относится вода, загрязненная радиоактивными элементами. Железобетонные и металлические резервуары расположены на поверхности, под землей или заглублены. Они имеют сложную систему защиты от протечек и повреждений при землетрясениях. 1.2.4. Использование в производстве технологий обратного водоснабжения, не требующего дополнительного водозабора и стока вод Химическая, металлургическая, нефтеперерабатывающая отрасли используют от 90 до 98% оборотной воды. Электростанции, автомойки, пищевые комбинаты тоже очищают и используют воду повторно. Если воду используют как охладитель, ей достаточно дать остыть в выделенном резервуаре. Жидкость после мытья деталей, автомобилей, продуктовых полуфабрикатов нуждается в многоступенчатой очистке. Технологии очищения зависят от вида загрязнений. Обычно обработка включает такие этапы: Механическая очистка: процеживание через решетки и пескоуловители, отстаивание; обессоливание в установке обратного осмоса. Применение технологий оборотного водоснабжения многократно уменьшает количество вредных выбросов, снижает фактическое водопотребление, на производствах сокращает потери компонентов сырья. В процессе очистки из загрязненной жидкости извлекают ценные вещества, попавшие в воду в процессе производства. 2 Физическая постановка задачи Рассмотрим нестационарную двумерную задачу переноса загрязняющей примеси от заданного источника в русле реки. В рассматриваемой области в начальный момент времени t=0 задано распределение концентрации загрязняющей примеси Сe=0. Считается, что скорость течения реки на прямолинейном участке постоянная в заданной области. Задан постоянно действующий источник выброса загрязнения внутри расчетной области. Необходимо найти распределение концентрации в заданной области течения реки в различные моменты времени для различных значений параметров (Рисунок 1). 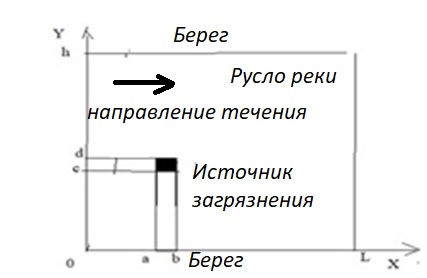 Рисунок 1 – Схема расчетной области 3 Математическая постановка задачи В связи с тем, что протяженность реки в горизонтальном направлении значительно превышает вертикальные размеры, математически процесс переноса загрязняющего вещества с течением времени в данной области описывается с помощью следующей системы дифференциальных уравнений (уравнений неразрывности, движения и диффузии) в горизонтальной плоскости с соответствующими начальными и граничными условиями: 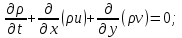 (1) (1)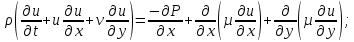 (2) (2)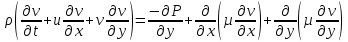 ; (3) ; (3)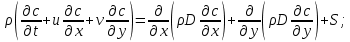 (4) (4)Начальные и граничные условия имеют следующий вид: 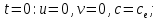 (5) (5)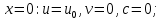 (6) (6)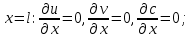 (7) (7)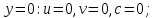 (8) (8)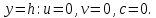 (9) (9)Где t – время, u, v – проекции вектора скорости на оси x, y, Р – давление, С – концентрациязагрязняющей примеси; ρ – плотность, µ, D – коэффициенты вязкости и диффузии для воды; h – ширина реки, L – длина участка реки. Источник S задан по формуле: 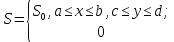 S0= (3, 6, 8) кг/(м3 с), a=6 м, b=7 м, c=2 м, d=2.5 м, u0=0.2 м/c, l=40 м, h=10 м 4 Численный метод решения Расчётную область разбиваем на некоторое число контрольных объёмов. Затем исходную систему уравнений интегрируем по каждому контрольному объёму. В результате получается алгебраическая система нелинейных уравнений. Для численного интегрирования исходной системы уравнений используется метод контрольного объёма (Рисунок 2) 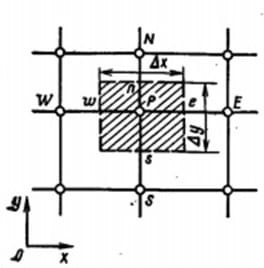 Рисунок 2 – Контрольный объём Вид двухмерного дискретного аналога можно записать как: 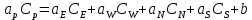 где 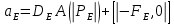 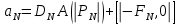 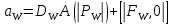 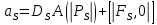 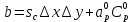 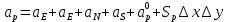 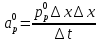 Здесь 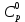 и и 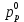 обозначают известные значения для времени t, а все другие величины (CР, CЕ, CW, CN, CS) представляют собой неизвестные величины для времени t+Δt. Соответствующие проводимости представим в виде: обозначают известные значения для времени t, а все другие величины (CР, CЕ, CW, CN, CS) представляют собой неизвестные величины для времени t+Δt. Соответствующие проводимости представим в виде: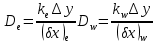 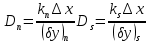 а числа Пекле: 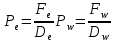 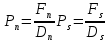 Коэффициенты в соседних точках аE, аW, аN и аS учитывают влияние конвекции и диффузии для четырех граней контрольного объема, которые зависят проводимости D. Член 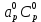 характеризует известную величину для контрольного объема (для времени t), отнесенную к шагу по времени. характеризует известную величину для контрольного объема (для времени t), отнесенную к шагу по времени.Проход по горизонтальным линиям: 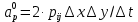 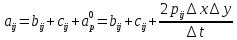 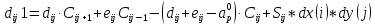 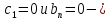 на границе области на границе областиОсуществляем расчёт по горизонтальной линии, применяя метод TDMA: Вычисленные коэффициенты уравнений используем для вычисления P1 и Q1 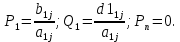 Используем рекуррентные соотношения 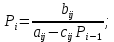 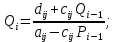 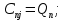 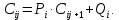 Проход по вертикальным линиям: 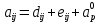 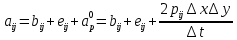 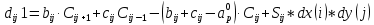 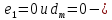 на границе области на границе областиВычислим коэффициенты: 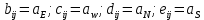 Далее осуществляем расчёт по вертикальной линии, применяя метод TDMA: Вычисленные коэффициенты уравнений используем для вычисления P1 и Q1 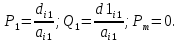 Используем рекуррентные соотношения 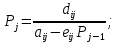 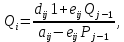 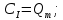 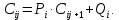 5 Результаты и их анализ На рис.3 представлено распределение концентрации в момент времени 1 с и источником загрязнения равным 3 кг/( 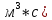 С=0.0007979 С=0.0005839 С =0.0004113 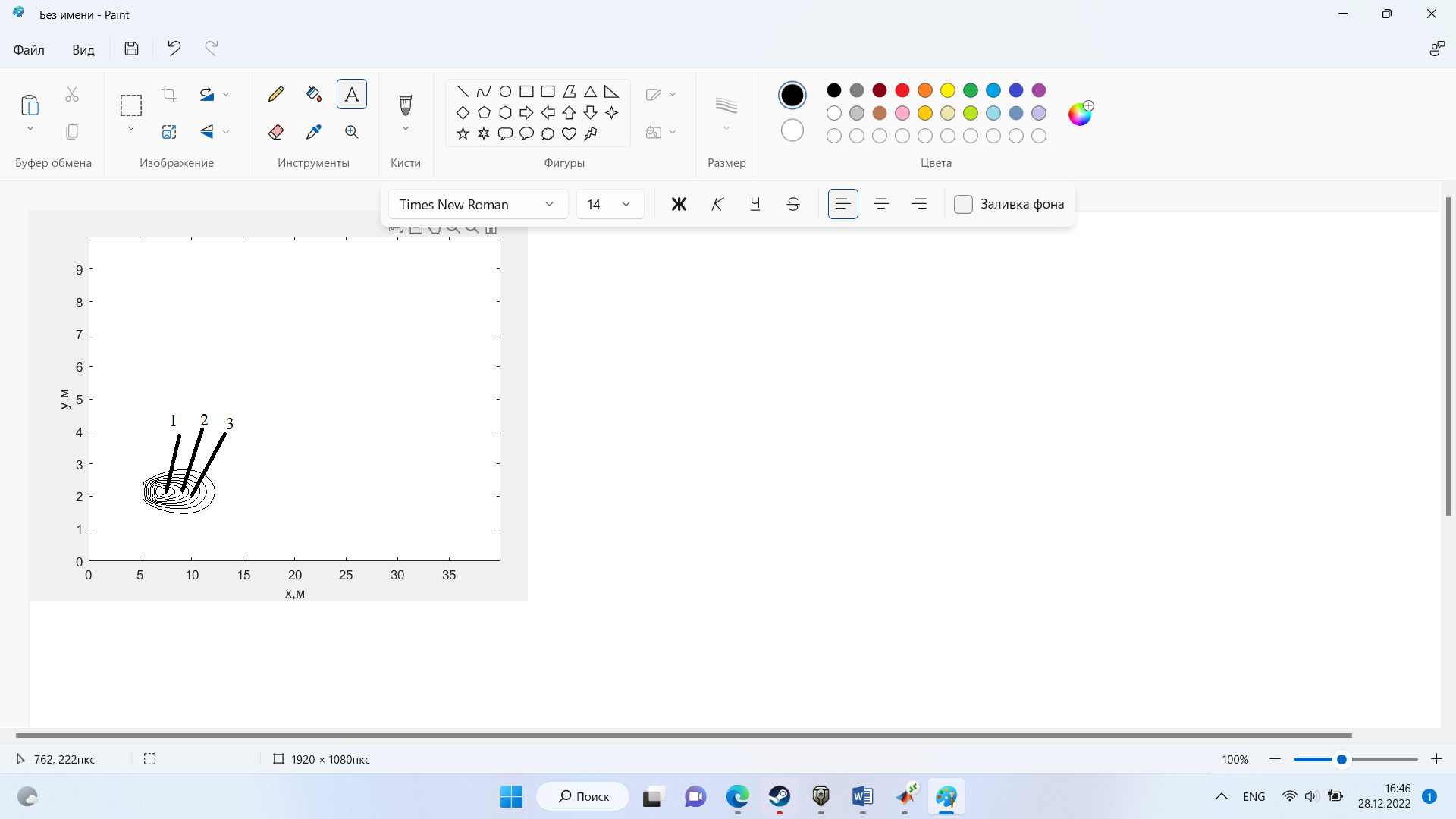 Рисунок 3 – график в момент времени 1с. На рис.4 представлено распределение концентрации в момент времени 5 с и источником загрязнения равным 3 кг/( 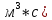 С=0.000802 С=0.0006011 С =0.0003986  Рисунок 4 – график в момент времени 5с. На рис.5 представлено распределение концентрации в момент времени 10 с и источником загрязнения равным 3 кг/( 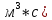 С=0.000802 С=0.0006257 С =0.0003986 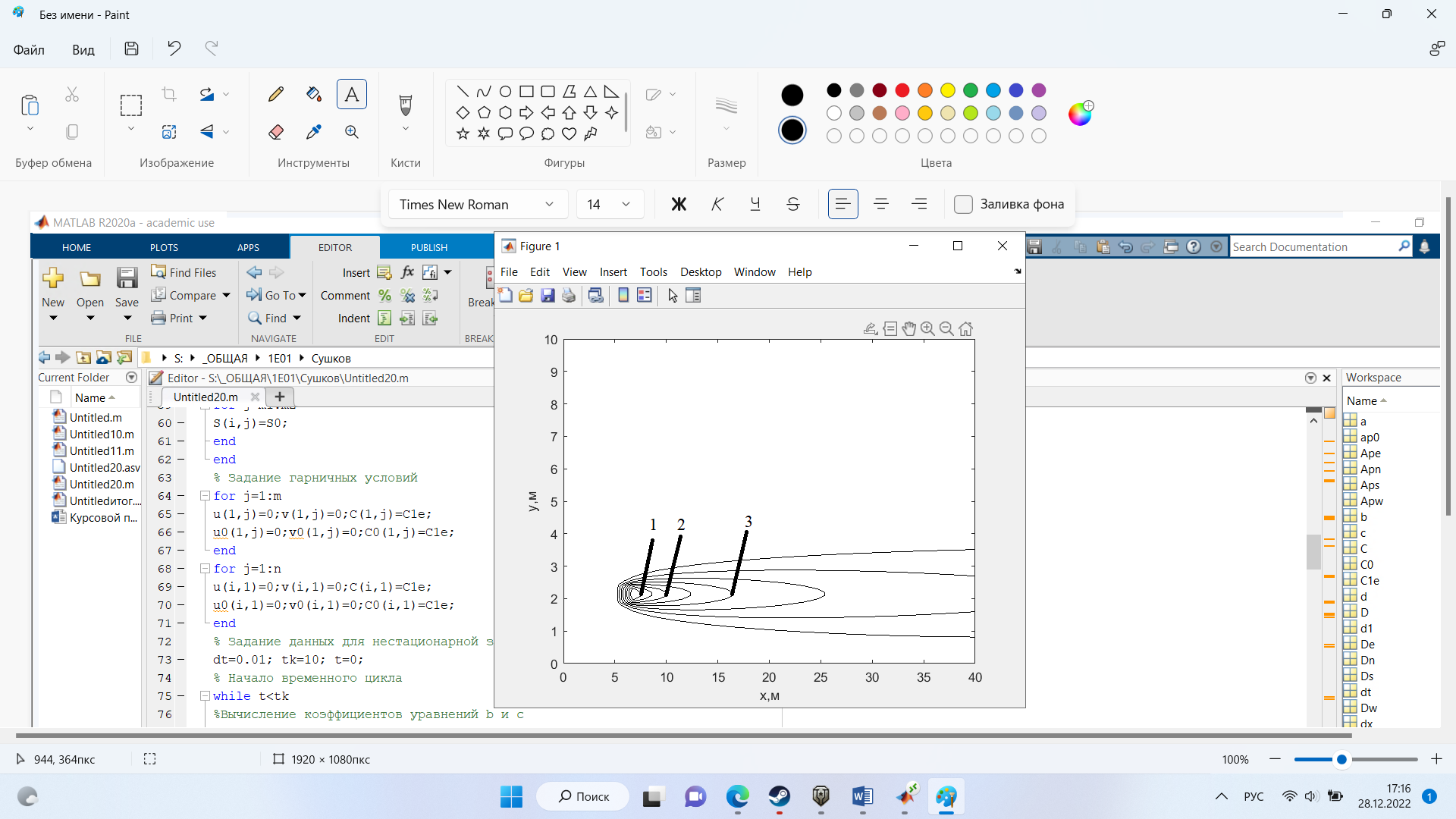 Рисунок 5 – график в момент времени 10с. На рис.6 представлено распределение концентрации в момент времени 10 с и источником загрязнения равным 6 кг/(  С=0.001604 С=0.001125 С =0.0007745  Рисунок 6 – график в момент времени 10с. На рис.7 представлено распределение концентрации в момент времени 5 с и источником загрязнения равным 6 кг/(  С=0.001604 С=0.001202 С =0.0007877  Рисунок 7 – график в момент времени 5с. На рис.8 представлено распределение концентрации в момент времени 1 с и источником загрязнения равным 6 кг/(  С=0.001596 С=0.001168 С =0.0008293  Рисунок 8 – график в момент времени 1с. На рис.9 представлено распределение концентрации в момент времени 1 с и источником загрязнения равным 9 кг/(  С=0.002544 С=0.002093 С =0.001553  Рисунок 9 – график в момент времени 1с. На рис.10 представлено распределение концентрации в момент времени 5 с и источником загрязнения равным 9 кг/( 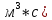 С=0.002321 С=0.00196 С =0.001001  Рисунок 10 – график в момент времени 5с. На рис.11 представлено распределение концентрации в момент времени 10 с и источником загрязнения равным 9 кг/( 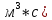 С=0.002321 С=0.002053 С =0.0009938  Рисунок 11 – график в момент времени 10с. 6 Выводы В результате проделанной работы можно сделать несколько вывод зависимости распределения загрязнения в водной среде от изменения параметров среды для данной задачи: С увеличением времени, распределение загрязнения в водной среде изменяется – увеличивается область концентраций; С увлечением мощности источника загрязнения, область концентраций также увеличивается. В пределах источника концентрация самая большая, а дальше идет на уменьшение 7 Литература Кичигин В.И. Водоотводящие системы промышленных предприятий: Учебное пособие. – М.: Издательство АСВ, 2011. – 656 с. Селина А.А. Проблемы очистки сточных вод / Селина А.А. // Промышленные страницы Сибири. – 2018. - № 130. – С. 30-32. Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. – М.: Энергоатомиздат, 1984. – 152 с. Дьяконов В.П. MATLAB. Полный самоучитель. – М.: ДМК Пресс, 2012. Загрязнение воды: пути решения экологической проблемы [Электронный ресурс]. – режим доступа: https://bezotxodov.ru 8 Приложение % Задание исходных данных L=40;h=10;u0=0.5;r0=1000.2;S0=9;D=80;C1e=0;n=100;m=100; % Задание размеров шагов по направлениям dx(1)=0; dx(n)=0; % Задание размеров шагов по направлениям x y: for i=2:n-1 dx(i)=L/(n-2); end for i=1:n-1 hx(i)=(dx(i)+dx(i+1))/2; end dy(1)=0 ;dy(m)=0; for j=2:m-1 dy(j)=h/(m-2); end for j=1:m-1 hy(j)=(dy(j)+dy(j+1))/2; end %Задание размеров шагов по направлениям x(1)=0; for i=1:n-1 x(i+1)=hx(i)+x(i); end % В цикле по j y(1)=0; for j=1:m-1 y(j+1)=hy(j)+y(j); end % Задание начальных условий for i=2:n for j=2:m C0(i,j)=0; C(i,j)=0; end end for i=1:n C(i,1)=0; C0(i,1)=0; end for j=1:m C(1,j)=0; C0(1,j)=0; end % Задание источника загрязнения n1=15; n2=18; m1=20; m2=25; %Задаем в двойном цикле по i и j S(i,j)=0 %Задаем источник загрязнения в двойном цикле for i=1:n for j=1:m S(i,j)=0; u(i,j)=0.5; v(i,j)=0; end end for i=n1:n2 for j=m1:m2 S(i,j)=S0; end end % Задание гарничных условий for j=1:m u(1,j)=0;v(1,j)=0;C(1,j)=C1e; u0(1,j)=0;v0(1,j)=0;C0(1,j)=C1e; end for j=1:n u(i,1)=0;v(i,1)=0;C(i,1)=C1e; u0(i,1)=0;v0(i,1)=0;C0(i,1)=C1e; end % Задание данных для нестационарной задачи dt=0.01; tk=10; t=0; % Начало временного цикла while t %Вычисление коэффициентов уравнений b и c for i=2:n-1 for j=2:m-1 Fe=r0*u(i,j); Fw=r0*u(i-1,j); De=D*dy(j)/hx(i); Dw=D*dy(j)/hx(i-1); Pe=Fe/De; Pw=Fw/Dw; Ape=max(0,(1-0.1*Pe)^5); Apw=max(0,(1-0.1*Pw)^5); b(i,j)=De*Ape+max(-Fe,0); c(i,j)=Dw*Apw+max(Fw,0); end end %коэффициентов уравнений d и e for i=2:n-1 for j=2:m-1 Fn=r0*v(i,j); Fs=r0*v(i,j-1); Dn=D*dx(i)/hy(j); Ds=D*dx(i)/hy(j-1); Pn=Fn/Dn; Ps=Fs/Ds; Apn=max(0,(1-0.1*Pn)^5); Aps=max(0,(1-0.1*Ps)^5); d(i,j)=Dn*Apn+max(-Fn,0); e(i,j)=Ds*Aps+max(Fs,0); end end %Вычисление коэф. для прохода по горизонтальным линиям for i=2:n-1 for j=2:m-1 ap0(i,j)=2*r0*dx(i)*dy(j)/dt; a(i,j)=b(i,j)+c(i,j)+ap0(i,j); d1(i,j)=d(i,j)*C0(i,j+1)+e(i,j)*C0(i,j-1)-(d(i,j)+e(i,j)-ap0(i,j))*C0(i,j)+S(i,j)*dx(i)*dy(j); end end %Проход по горизонтальным линиям %Открываем цикл по j for j=2:m-1 %При x=L:dc/dx=0 учтем это Гу %Уравнение на правой границе а(n,j)*C(n,j)=c(n,j)*C(n-j) %Тогда a(n,j)=1; c(n,j)=1; b(n,j)=0; d1(n,j)=0; P(1)=0; Q(1)=0; for i=2:n P(i)=b(i,j)/(a(i,j)-c(i,j)*P(i-1)); Q(i)=(d1(i,j)+c(i,j)*Q(i-1))/(a(i,j)-c(i,j)*P(i-1)); end C(n,j)=Q(n); i=n-1; while i>1 C(i,j)=P(i)*C(i+1,j)+Q(i); i=i-1; end for i=2:m C0(i,j)=C(i,j); end end for i=2:n-1 for j=2:m-1 a(i,j)=d(i,j)+e(i,j)+ap0(i,j); d1(i,j)=b(i,j)*C0(i+1,j)+c(i,j)*C0(i-1,j)-(b(i,j)+c(i,j)-ap0(i,j))*C0(i,j)+S(i,j)*dx(i)*dy(j); end end for i=2:n-1 %при y=h: dc/dy=0 учтем это ГУ %уравнение на верхней границе a(i,m)*C(i,m)=e(i,m)*c(i,m-1); a(i,m)=1; e(i,m)=1; d(i,m)=0; d1(i,m)=0; P(1)=0; Q(1)=0; %Решаем TDMA систему уравнений: for j=2:m P(j)=d(i,j)/(a(i,j)-e(i,j)*P(j-1)); Q(j)=(d1(i,j)+e(i,j)*Q(j-1))/(a(i,j)-e(i,j)*P(j-1)); end C(i,m)=Q(m); j=m-1; while j>1 C(i,j)=P(j)*C(i,j+1)+Q(j); j=j-1; end for j=2:m C0(i,j)=C(i,j); end end t=t+dt; end %Рисование графика на данный момент времени contour(x,y,C','k') xlabel('x,м'); ylabel('y,м') | ||||||||||||||||||||||||||||||||||||||||||||||||
