Курсовой проект по дисциплине Металлические конструкции включая сварку Тема Проектирование сборных железобетонных конструкций многоэтажного каркасного здания
 Скачать 2.68 Mb. Скачать 2.68 Mb.
|
5.1. Расчетные длины колонныТак как 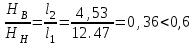 (5.1.1) (5.1.1)и 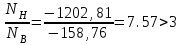 (5.1.2) (5.1.2)то значения коэффициентов 1 и 2 находим по табл. 14.1 [6]: 1 = 2; 2 = 3.  5.1.1. Выкопировка таблицы 14.1 [6] Расчетные длины колонны в плоскости рамы: - для нижней части колонны 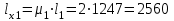 см; (5.1.3) см; (5.1.3)- для верхней части колонны 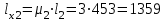 см. (5.1.4) см. (5.1.4)Расчетные длины колонны из плоскости рамы 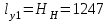 см; (5.1.5) см; (5.1.5)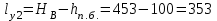 см. (5.1.6) см. (5.1.6)5.2. Подбор сечения верхней части колонныСечение верхней части колонны принимаем в виде сварного двутавра со стороной h = 450 мм. Для симметричного двутавра по учебнику принимаем 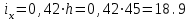 см (5.2.1) см (5.2.1)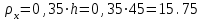 см (5.2.2) см (5.2.2)В таком случае условная гибкость верхней части колонн в плоскости рамы 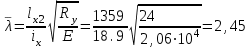 (5.2.3) (5.2.3)Относительный эксцентриситет: 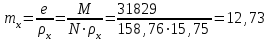 (5.2.4) (5.2.4)По таблице Д.2 [4] находим, что коэффициент влияния формы сечения в первом приближении 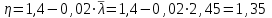 (5.2.5) (5.2.5)Тогда приведенный относительный эксцентриситет: 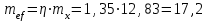 (5.2.6) (5.2.6)По табл. Д.4 [4] находим, что коэффициент устойчивости при сжатии с изгибом е = 0,05. 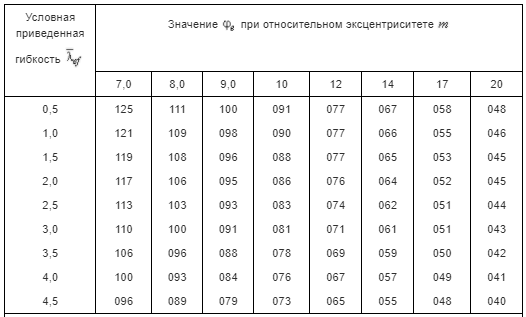 5.2.1. Выкопировка таблицы Д.4 из [4] Таблица 5.2.1. Двойная интерполяция 𝜑
Требуемая площадь сечения: 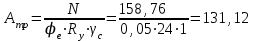 см2. см2.5.2.1. Компоновка сеченияПредварительно примем толщину полки tf = 20 мм, тогда высота стенки: 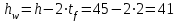 см. (5.2.1.1) см. (5.2.1.1)Требуемую толщину стенки подберем из условия ее местной устойчивости. По учебнику предельная условная гибкость стенки двутаврового сечения (при т > 1 и условной гибкости < 2,0) определяется как: 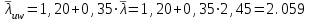 (5.2.1.2) (5.2.1.2)тогда 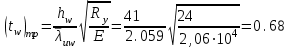 см (5.2.1.3) см (5.2.1.3)принимаем tw = 7 мм. Требуемая площадь сечения одной полки двутавра: 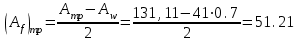 см2 (5.2.1.4) см2 (5.2.1.4)Так как ранее принятая толщина полки tf = 20 мм = 2см , ширина полки составит: 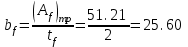 см (5.2.1.5) см (5.2.1.5)окончательно примем bf = 26 см. Получим следующее сечение: 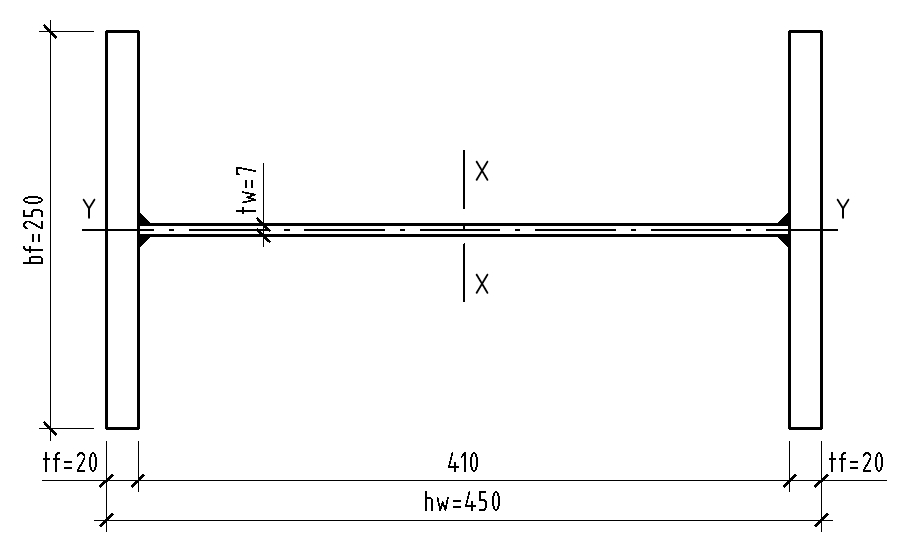 Рисунок 5.2.1.1 Принятое сечение двутавра верхней части колонны Согласно табл. 29 [4] устойчивость полки обеспечена, так как 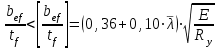 (5.2.1.6) (5.2.1.6)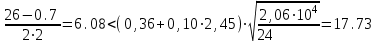 Геометрические характеристики сечения: - площадь поперечного сечения: 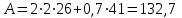 см2 (5.2.1.7) см2 (5.2.1.7)- момент инерции сечения относительно оси х-х: 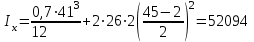 см4 (5.2.1.8) см4 (5.2.1.8)- момент инерции сечения относительно оси у-у: 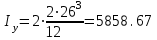 см4 (5.2.1.9) см4 (5.2.1.9)- радиус инерции сечения относительно оси х-х: 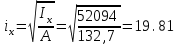 см (5.2.1.10) см (5.2.1.10)- радиус инерции сечения относительно оси у-у: 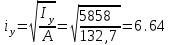 см (5.2.1.11) см (5.2.1.11)- момент сопротивления: 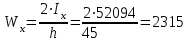 см3 (5.2.1.12) см3 (5.2.1.12)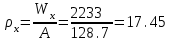 см (5.2.1.13) см (5.2.1.13)-гибкость стержня верхней части колонны оси х-х: 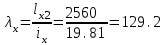 (5.2.1.14) (5.2.1.14)-условная гибкость стержня верхней части колонны оси х-х: 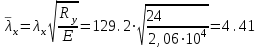 (5.2.1.15) (5.2.1.15)-гибкость стержня верхней части колонны оси y-y: 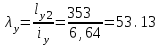 (5.2.1.16) (5.2.1.16)-условная гибкость стержня верхней части колонны оси y-y: 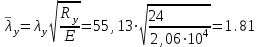 (5.2.1.17) (5.2.1.17)5.2.2. Проверка устойчивости в плоскости действия моментаОтносительный эксцентриситет: 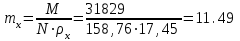 (5.2.2.1) (5.2.2.1)Отношение площадей полки и стенки: 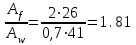 (5.2.2.2) (5.2.2.2)По табл. Д.2 [5] находим, что коэффициент влияния формы сечения = 1,4-0,02*λ= 14-0.02 * 4.42 = 1,31. Тогда приведенный относительный эксцентриситет: 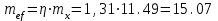 (5.2.2.3) (5.2.2.3)По табл. Д.3 [4] находим, что коэффициент е = 0,07. 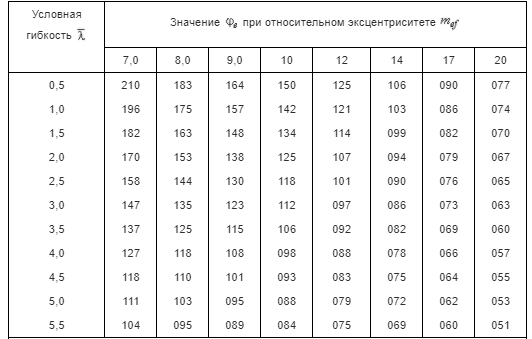 Рисунок 5.2.2.1. Выкопировка таблицы Д.3 из [5] Проверим устойчивость 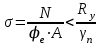 (5.2.2.4) (5.2.2.4)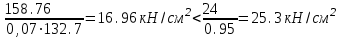 5.2.3. Проверка устойчивости из плоскости действия моментаЭту проверку выполним по формуле: где у – коэффициент устойчивости, при у = 1,81 по табл. Д.1 [4] у = 0,853; 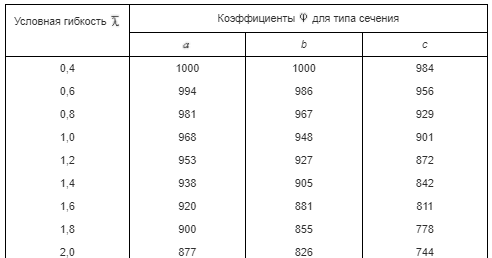 Рисунок 5.2.3.1 Таблица Д.1 [5] Таблица 5.2.3.1 Интерполяция φ
с – коэффициент, учитывающий влияние момента Мх при изгибно-крутильной форме потере устойчивости. Для определения тх найдем максимальный момент в средней части расчетной длины стержня при сочетании нагрузок 1, 2, 3*, 4, 5*. 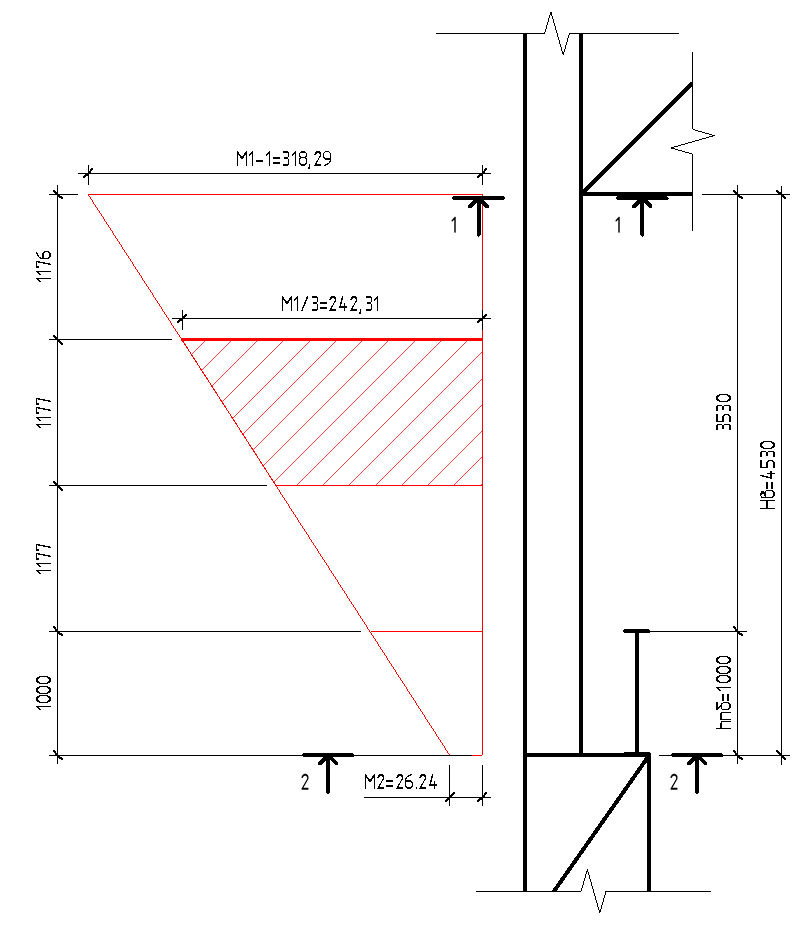 Рисунок 5.2.3.2. Расчетный момент в пределах средней трети расчетной длины колонны За расчетный примем максимальный момент в пределах средней трети расчетной длины. Проверка: 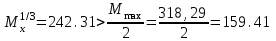 кНм (5.2.3.2) кНм (5.2.3.2)Тогда 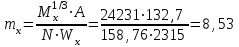 (5.2.3.3) (5.2.3.3)При 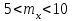 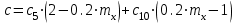 (5.2.3.4) (5.2.3.4), , - коэффициенты, определяемые по прил. 12 учебника. При 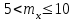 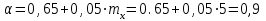 При 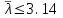 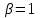 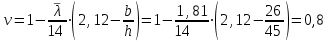 Т.о. определим 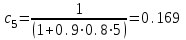 (5.2.3.5) (5.2.3.5)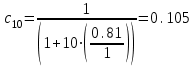 (5.2.3.6) (5.2.3.6)Тогда по (5.2.3.4): 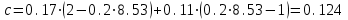 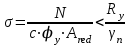 (5.2.3.6) (5.2.3.6)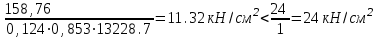 (5.2.3.7) (5.2.3.7)Так как mef < 20 и верхняя часть колонны не имеет ослабления сечения, то проверку несущей способности колонны производить нет необходимости. | ||||||||||||||||||||||||||||
