курсовая работа. КП МЭИ. Курсовой проект по дисциплине Строительные конструкции Тема Проектирование несущих железобетонных конструкций многоэтажного каркасного здания из сборного железобетона
 Скачать 1.02 Mb. Скачать 1.02 Mb.
|
|
Определение усилий в ригеле Расчетная схема ригеля – однопролетная шарнирно опертая балка пролетом 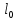 . Вычисляем значение максимального изгибающего момента M и максимальной поперечной силы Q от полной расчетной нагрузки: . Вычисляем значение максимального изгибающего момента M и максимальной поперечной силы Q от полной расчетной нагрузки: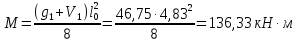 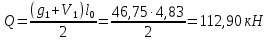 Характеристики прочности бетона и арматуры:  25 – бетон тяжелый класса B30, расчетное сопротивление при сжатии 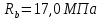 , при растяжении , при растяжении 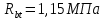 , , 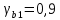 ; ; – арматура продольная рабочая класса А500С диаметром 10 – 40 мм, расчетное сопротивление 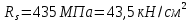 , поперечная рабочая арматура класса А400 диаметром 6 – 8 мм, , поперечная рабочая арматура класса А400 диаметром 6 – 8 мм, 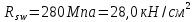 (табл. 6.15 [2]). (табл. 6.15 [2]).3.3. Расчет ригеля по прочности нормальных сечений при действии изгибающего момента Определяем высоту сжатой зоны: х = ξ·h0, где h0 — рабочая высота сечения ригеля (рис. 6);  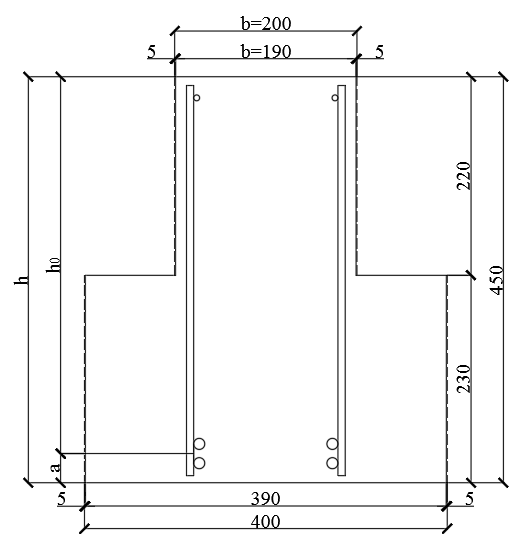 Рис. 6 Расчетное сечение ригеля 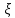 – относительная высота сжатой зоны, определяемая в зависимости от – относительная высота сжатой зоны, определяемая в зависимости от 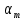 : :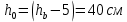 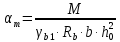 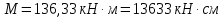 Rb = 17 МПа = 1,7 кН/см2 b — ширина сечения ригеля; b = 20 см; 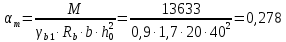 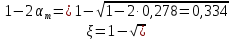 Высота сжатой зоны х = 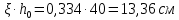 Граница сжатой зоны проходит в узкой части сечения ригеля, следовательно, расчет ведем как для прямоугольного сечения. Расчет по прочности нормальных сечений   26 производится в зависимости от соотношения относительной высоты сжатой зоны бетона и граничной относительной высоты 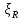 , пр и которой предельное состояние элемента наступает по сжатой зоне бетона одновременно с достижением в растянутой арматуре напряжения, равного расчетному сопротивлению Rs. Значение , пр и которой предельное состояние элемента наступает по сжатой зоне бетона одновременно с достижением в растянутой арматуре напряжения, равного расчетному сопротивлению Rs. Значение 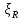 определяется по формуле: определяется по формуле: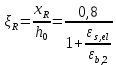 Где 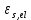 – относительная деформация растянутой арматуры при напряжениях, равных – относительная деформация растянутой арматуры при напряжениях, равных 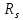 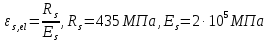 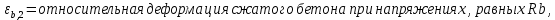 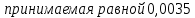 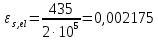 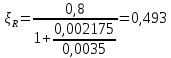 значение 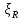 можно определить по табл. 3.2 [4] или по прил. 11, так как можно определить по табл. 3.2 [4] или по прил. 11, так как 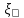 < < 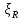 . Площадь сечения растянутой арматуры определяется по формуле . Площадь сечения растянутой арматуры определяется по формуле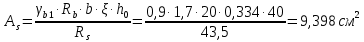 Если 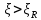 , следует увеличить сечение ригеля или повысить класс бетона или запроектировать в сжатой зоне сжатую рабочую арматуру с помощью , следует увеличить сечение ригеля или повысить класс бетона или запроектировать в сжатой зоне сжатую рабочую арматуру с помощью 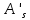 . .Если 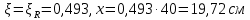 , т.е. при , т.е. при 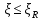 граница границасжатой зоны всегда проходит в узкой части сечения ригеля. По найденной площади сечения растянутой арматуры по сортаменту подбираем 4Ø18 А500С 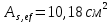 ; ;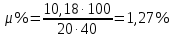 Площадь подобранной арматуры должна быть больше требуемой по расчету площади или равна ей. Можно подобрать стержни одинакового диаметра, так чтобы площадь подобранной арматуры отличалась бы от площади требуемой арматуры незначительно.  3.4 Расчет ригеля по прочности при действии поперечных сил 3.4 Расчет ригеля по прочности при действии поперечных силРасчет ригеля по прочности при действии поперечных сил производится на основе модели наклонных сечений. Ригель опирается на колонну с помощью консолей, скрытых в его подрезке (рис. 7), т.е. имеет место резко изменяющаяся высота сечения ригеля на опоре. При расчете по модели наклонных сечений должны быть обеспечены прочность ригеля по бетонной полосе между наклонными сечениями, по наклонному сечению на действие поперечной силы и изгибающего момента. Для ригелей с подрезками на опорах производится расчет по поперечной силе для наклонных сечений, проходящих у опоры консоли, образованной подрезкой. При этом в расчетные формулы вводится рабочая высота 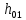 короткой консоли ригеля. Таким образом, в качестве расчетного принимаем прямоугольное сечение с размерами короткой консоли ригеля. Таким образом, в качестве расчетного принимаем прямоугольное сечение с размерами 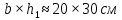 , в котором действует поперечная сила , в котором действует поперечная сила 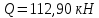 от полной расчетной нагрузки. Рабочая высота сечения ригеля в подрезке составляет от полной расчетной нагрузки. Рабочая высота сечения ригеля в подрезке составляет 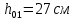 , вне подрезки (у опор) , вне подрезки (у опор) 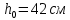 , в средней части пролета , в средней части пролета 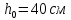 . .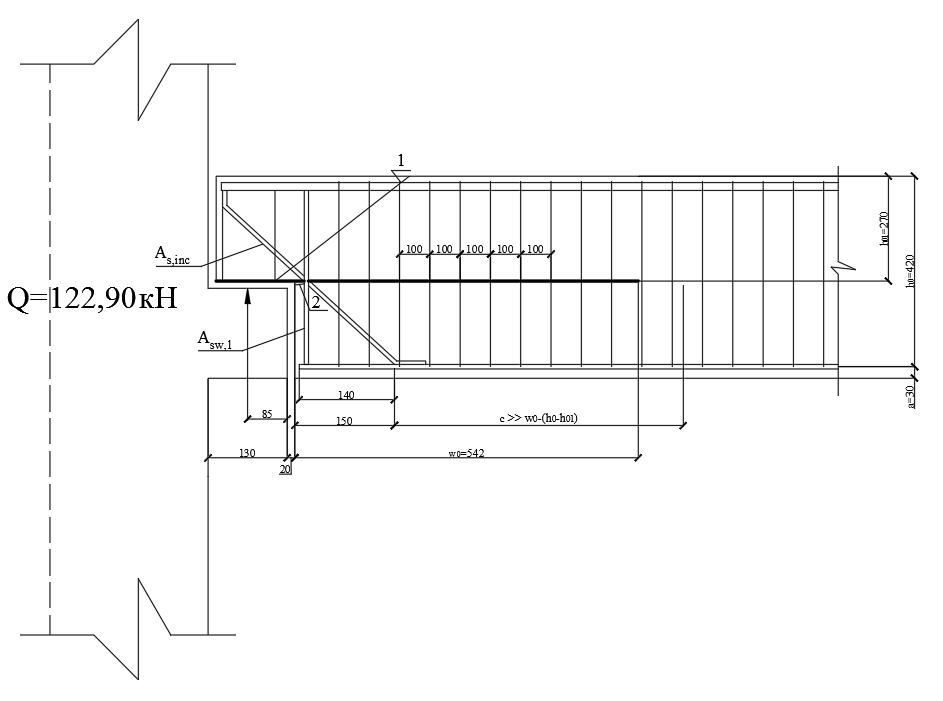 Рис.7 – Наклонное сечение на приопорном участке ригеля с подрезкой: 1 – при расчете по поперечной силе; 2 – горизонтальная трещина отрыва у входящего угла подрезки При диаметре нижних стержней продольной рабочей арматуры ригеля 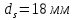 с учетом требований назначаем поперечные стержни (хомуты) Ø8 А400. Их шаг на приопорном участке предварительно принимаем по конструктивным соображениям с учетом требований назначаем поперечные стержни (хомуты) Ø8 А400. Их шаг на приопорном участке предварительно принимаем по конструктивным соображениям 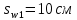 , что в соответствии с не превышает , что в соответствии с не превышает 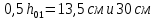 . Значения прочностных характеристик бетона класса В30, входящие в расчетные зависимости, принимаем с учетом коэффициента условий работы . Значения прочностных характеристик бетона класса В30, входящие в расчетные зависимости, принимаем с учетом коэффициента условий работы 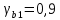 . .Расчет ригеля по бетонной полосе между наклонными трещинами производится из условия: 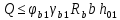 , ,где 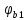 – коэффициент, принимаемый равным 0,3. – коэффициент, принимаемый равным 0,3.Проверка этого условия дает: 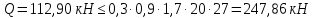 , ,т.е. принятые размеры сечения ригеля в подрезке достаточны. Проверяем, требуется ли поперечная арматура по расчету из условия: 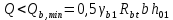 , ,т.е. 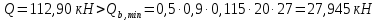 , поэтому расчет поперечной арматуры необходим. , поэтому расчет поперечной арматуры необходим.Находим погонное усилие в хомутах для принятых выше параметров поперечного армирования 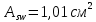 (2Ø8 А400), (2Ø8 А400), 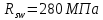 , , 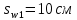 : :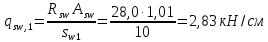 . .Расчет ригеля с рабочей поперечной арматурой по наклонному сечению производится из условия: 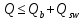 , ,где 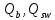 – поперечная сила, воспринимаемые соответственно бетоном и поперечной арматурой в наклонном сечении, которые находятся по формулам: – поперечная сила, воспринимаемые соответственно бетоном и поперечной арматурой в наклонном сечении, которые находятся по формулам: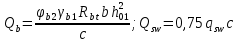 , ,где 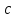 – длина проекции наклонного сечения на продольную ось элемента; – длина проекции наклонного сечения на продольную ось элемента;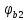 – коэффициент, принимаемый равным 1,5 – коэффициент, принимаемый равным 1,5  Подставляем эти выражения, из условия минимума несущей способности ригеля по наклонному сечению в виде Подставляем эти выражения, из условия минимума несущей способности ригеля по наклонному сечению в виде 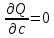 находим наиболее опасную длину проекции наклонного сечения, равную: находим наиболее опасную длину проекции наклонного сечения, равную: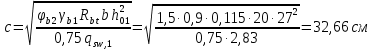 которая должна быть не более 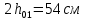 . С учетом этой величины условие преобразуем к виду: . С учетом этой величины условие преобразуем к виду: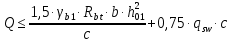 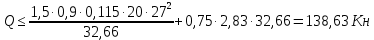 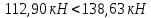 т.е. условие прочности ригеля по наклонному сечению в подрезке при действии поперечной силы соблюдается. Необходимо также убедиться в том, что принятый шаг хомутов 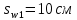 не превышает максимального шага хомутов не превышает максимального шага хомутов 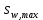 , при котором еще обеспечивается прочность ригеля по наклонному сечению между двумя соседними хомутами, т.е.: , при котором еще обеспечивается прочность ригеля по наклонному сечению между двумя соседними хомутами, т.е.: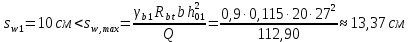 Выясним теперь, на каком расстоянии от опор в соответствии с характером эпюры поперечных сил в ригеле шаг поперечной арматуры может быть увеличен. Примем шаг хомутов в средней части пролета равным 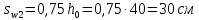 , что не превышает 500 мм. Погонное усилие в хомутах для этого участка составляет: , что не превышает 500 мм. Погонное усилие в хомутах для этого участка составляет: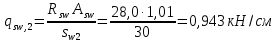 что не меньше минимальной интенсивности этого усилия, при которой поперечная арматура учитывается в расчете: 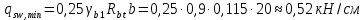 Очевидно, что условие 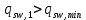 для опорных участков ригеля соблюдается с ещё большим запасом. для опорных участков ригеля соблюдается с ещё большим запасом.При действии на ригель равномерно распределенной нагрузки 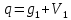 длина участка с интенсивностью усилия в хомутах длина участка с интенсивностью усилия в хомутах 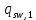 принимается не менее значения принимается не менее значения 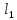 , определяется по формуле: , определяется по формуле: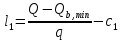 и не менее и не менее 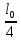 , ,  где где 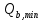 – то же, что в формуле 8.1.33 [2], но при замене – то же, что в формуле 8.1.33 [2], но при замене 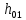 на рабочую высоту сечения ригеля в пролете на рабочую высоту сечения ригеля в пролете 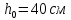 ; ;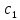 – наиболее опасная длина проекции наклонного сечения для участка, где изменяется шаг хомутов; определяется по формуле: – наиболее опасная длина проекции наклонного сечения для участка, где изменяется шаг хомутов; определяется по формуле: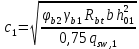 с заменой в ней 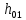 на на 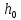 , а также , а также 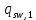 на на 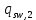 , но не более 2 , но не более 2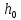 Тогда имеем: 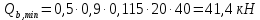 ; ;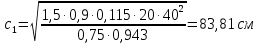 Поскольку 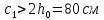 , то принимаем , то принимаем 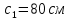 ; ; 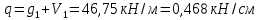 , тогда: , тогда: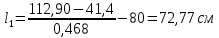 В ригелях с подрезками у концов последних устанавливаются дополнительные хомуты и отгибы для предотвращения горизонтальных трещин отрыва у входящего угла подрезки (рис. 8). Эти хомуты и отгибы должны удовлетворять условию прочности: 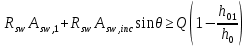 , ,где 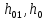 – рабочая высота сечения ригеля соответственно в короткой консоли подрезки и вне ее. – рабочая высота сечения ригеля соответственно в короткой консоли подрезки и вне ее.Для рассматриваемого примера со сравнительно небольшим значением поперечной силы примем дополнительные хомуты у конца подрезки в количестве 2Ø12 А500С с площадью сечения 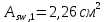 , отгибы использовать не будем. Тогда из проверки условия прочности: , отгибы использовать не будем. Тогда из проверки условия прочности: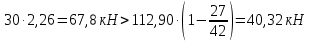 т.е. установленных дополнительных хомутов достаточно для предотвращения горизонтальных трещин отрыва у входящего угла подрезки. Расчет по прочности наклонного сечения, проходящего через входящий угол подрезки, на действие изгибающего момента производится из условия: 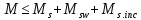 , , где где 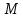 – момент в наклонном сечении с длиной проекции « – момент в наклонном сечении с длиной проекции «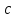 » на продольную ось элемента; » на продольную ось элемента;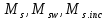 – моменты, воспринимаемые соответственно продольной и поперечной арматурой, а также отгибами, пересекаемыми рассматриваемым наклонным сечением, относительно противоположного конца наклонного сечения (в отсутствии отгибов – моменты, воспринимаемые соответственно продольной и поперечной арматурой, а также отгибами, пересекаемыми рассматриваемым наклонным сечением, относительно противоположного конца наклонного сечения (в отсутствии отгибов 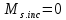 ). ).В рамках курсового проекта этот расчет не выполняется. Построение эпюры материалов Продольная рабочая арматура в полете 4Ø18 А500С. Площадь этой арматуры 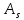 определена из расчета на действие максимального изгибающего момента в середине пролета. В целях экономии арматуры по мере уменьшения изгибающего момента к опорам два стержня обрываются в пролете, а два других доводятся до опор. Если продольная арматура разного диаметра, то до опор доводятся два стержня большего диаметра. определена из расчета на действие максимального изгибающего момента в середине пролета. В целях экономии арматуры по мере уменьшения изгибающего момента к опорам два стержня обрываются в пролете, а два других доводятся до опор. Если продольная арматура разного диаметра, то до опор доводятся два стержня большего диаметра.Площадь рабочей арматуры 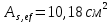 . Определяем изгибающий момент, воспринимаемый сечением ригеля с полной запроектированной арматурой 4Ø18 А500С ( . Определяем изгибающий момент, воспринимаемый сечением ригеля с полной запроектированной арматурой 4Ø18 А500С (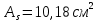 ). ).Из условия равновесия: 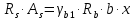 , ,где 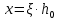 ; ;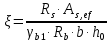 ; ;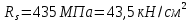 ; ;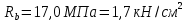 ; ;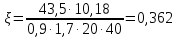 ; ;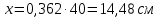 Изгибающий момент, воспринимаемый сечением ригеля, определяется из условия равновесия: 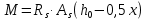 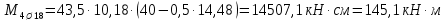 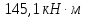 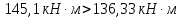 , т.е. больше действующего изгибающего момента от полной нагрузки, это значит, что прочность сечения обеспечена. , т.е. больше действующего изгибающего момента от полной нагрузки, это значит, что прочность сечения обеспечена. До опоры доводятся 2Ø18 А500С, До опоры доводятся 2Ø18 А500С, 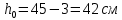 ; ; 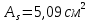 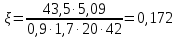 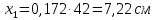 Определяем изгибающий момент, воспринимаемый сечением ригеля с рабочей арматурой в виде двух стержней, доводимых до опоры: 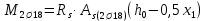 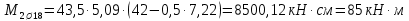 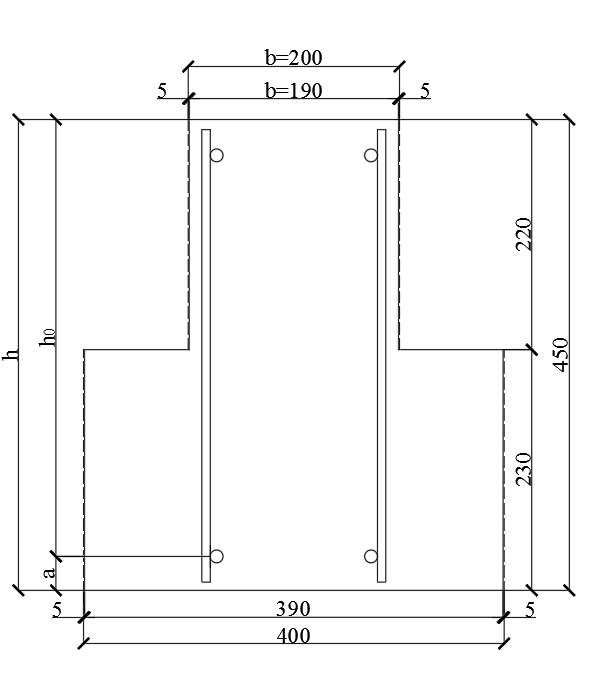 Рис.8 – Расчетное сечение ригеля в месте обрыва арматуры Откладываем в масштабе на эпюре моментов полученные значения изгибающих моментов 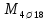 и и 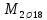 и определяем место теоретического обрыва рабочей арматуры – это точки пересечения эпюры моментов с горизонтальной линией, соответствующей изгибающему моменту, воспринимаемому сечением ригеля с рабочей арматурой в виде двух стержней и определяем место теоретического обрыва рабочей арматуры – это точки пересечения эпюры моментов с горизонтальной линией, соответствующей изгибающему моменту, воспринимаемому сечением ригеля с рабочей арматурой в виде двух стержней 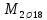 (рис. 9). (рис. 9). Эпюра моментов для этого должна быть построена точно с определением значений изгибающих моментов в 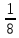 , в , в 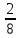 и в и в 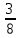 полета. полета.Изгибающий момент в любом сечении ригеля определяется по формуле: 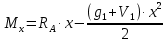  где где 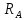 – опорная реакция; – опорная реакция; 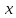 – текущая координата. – текущая координата.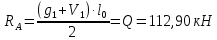 При 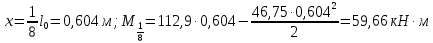 При 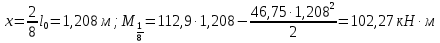 При 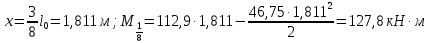 Длина анкеровки обрываемых стержней определяется по следующей зависимости: 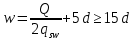 где 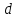 – диаметр обрываемой арматуры – диаметр обрываемой арматурыПоперечная сила 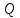 определяется графически в месте теоретического обрыва, в данном случае определяется графически в месте теоретического обрыва, в данном случае 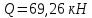 Поперечные стержни Ø8 А400 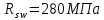 с с 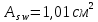 в месте теоретического обрыва имеют шаг 10 см. в месте теоретического обрыва имеют шаг 10 см.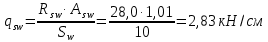 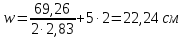 , что меньше , что меньше 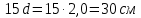 Принимаем 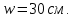 Место теоретического обрыва арматуры можно определить аналитически. Для этого общее выражения для изгибающего момента нужно приравнять моменту воспринимаемому сечением ригеля с арматурой 2Ø18 А500: 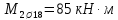 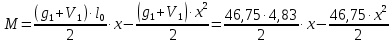 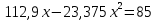 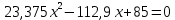 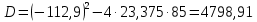 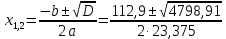 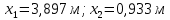 Это точки теоретического обрыва арматуры. Длина обрываемого стержня будет равна 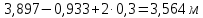 Принимаем длину обрываемого стержня 3,6 м. Определяем аналитически величину поперечной силы в месте теоретического обрыва арматуры: 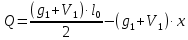 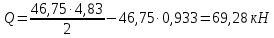 Графически поперечная сила была принята 69,26 кН с достаточной степенью точности. 4.Расчет и конструирование колонны Для проектируемого 8-этажного здания принята сборная железобетонная колонна сечением 40 × 40 см. Для колонн применяется тяжелый бетон классов по прочности на сжатие не ниже В15, а для сильно загруженных – не ниже В25. Армируются колонны продольными стержнями диаметром 16…40 мм из горячекатаной стали А400, А500С и поперечными стержнями преимущественно из горячекатаной стали класса А240. 4.1Исходные данные Нагрузка на 1 м2 перекрытия принимается такой же, как и в предыдущих расчетах (см. табл. 2). Материалы для колонны: Бетон – тяжелый класса по прочности на сжатие В25, расчетное сопротивление при сжатии 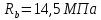 (табл. 6.8 [2], прил. 4). (табл. 6.8 [2], прил. 4).Арматура: – продольная рабочая класса А500С (диаметр 16…40 мм), расчетное сопротивление 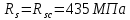 (табл. 6.14 [2], прил. 7); (табл. 6.14 [2], прил. 7);– поперечная – класса А240.  |
