Курсовой проект по дисциплине Теплофизические процессы в устройствах рэс

• Название: Курсовой проект по дисциплине Теплофизические процессы в устройствах рэс
• Дата: 20.01.2023
• Размер: 214 Kb.
• Имя файла: Kursovaya_rabota_po_teplofizike(1).doc
• Тип: Курсовой проект; #896643

ФЕДЕРАЛЬНОЕ АГЕНТСВО ПО ОБРАЗОВАНИЮ

Российской Федерации

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ГОУВ ПО «ВГТУ»

Радиотехнический факультет

Кафедра конструирования и производства радиоаппаратуры
КУРСОВОЙ ПРОЕКТ
по дисциплине «Теплофизические процессы в устройствах РЭС»
Тема: «Расчет тепловых характеристик блоков РЭС при различных условиях охлаждения»

Разработал студент(ка) РК- 083 Шорошова Е.И

(группа, подпись, дата, инициалы, фамилия)

Руководитель Ципина Н.В

(подпись, дата, инициалы, фамилия)
Члены комиссии ___________________________________________

(подпись, дата, инициалы, фамилия)
Нормоконтролер ____________________________________________

(подпись, дата, инициалы, фамилия)
Проект защищен______________ Оценка _____________

Воронеж 2010

Замечания руководителя

Содержание

Введение 3

1 Анализ технического задания 4

2 Выбор системы охлаждения 5

3 Расчетная часть

3.1 Расчет теплового режима блока

3.1.1 Приближенная методика расчета теплового режима блока 7

3.1.2 Расчет теплового режима блока 10

3.2 Выбор конструкции и расчет параметров радиатора для элемента с наиболее тяжелым тепловым режимом

3.2.1 Эффективный коэффициент теплоотдачи радиатора 12

3.2.2 Методика выбора и расчета радиатора 15

3.2.3 Выбор конструкции и расчет параметров радиатора 17

Заключение 19

Список литературы 20

Введение

Специалисты, занимающиеся проектированием радиоэлектронных аппаратов, все большее внимание обращают на их тепловые режимы. Интерес к этой задаче объясняется следующими причинами. Значительная часть различных форм энергии в радиоэлектронном аппарате превращается в тепловую, что приводит к повышению температуры деталей в аппарате. Известно, что надежность деталей падает с повышением их температуры. Увеличение температуры в аппарате вызывает ухудшение изоляционных свойств отдельных материалов, изменение плотности и подвижности носителей тока в полупроводниках, снижение индуктивности насыщения в сердечниках, общее увеличение интенсивности старения материалов и т. д. Все эти факторы могут привести к искажению сигналов на выходе аппарата или даже к выходу аппарата из строя. Следовательно, нормальный тепловой режим радиоэлектронного аппарата является необходимым условием его надежной работы.

Для обеспечения нормального теплового режима аппарата следует пытаться выбрать оптимальную систему его охлаждения и габариты, определенным образом разместить отдельные части аппарата относительно друг друга. Таким образом, конструкция радиоэлектронного аппарата во многом определяется его тепловым режимом.


1 Анализ технического задания

Анализируя исходные данные, указанные в техническом задании, можно сказать, что в блоке выделяется сравнительно небольшая мощность, поэтому в качестве системы охлажде­ние предпочтительнее использовать воздушное охлаждение. Температура окружающей среды равная 293 К является средней и будет незначительно влиять на тепловой режим блока. Давление окружающей среды – 0.08 МПа, что является нормальным атмосферным давлением.

Мощности, рассеиваемые элементами: для первого транзистора КТ805– 7.9 Вт, для второго КТ809 – 4.3 Вт, для третьего КТ805 – 7.8 Вт. Исходя из этих данных, можно сделать вывод, что для первого транзистора необходимо будет выбрать и рассчитать радиатор.

Транзистор КТ805 имеет цилиндрическую форму с диаметром основания 12 мм. Для него критической температурой p-n перехода является 150 °С, а критической температурой корпуса - 100 °С . Тепловое сопротивление переход – корпус составляет 2 °С/Вт.

Проанализировав исходные данные можно сделать вывод, что их достаточно для теплового расчета блока.

2 Выбор системы охлаждения

Способ охлаждения во многом определяет конструкцию РЭА, поэтому его необходимо выбирать на ранней стадии проектирования, т. е. на стадии технического предложения или эскизного проекта. Неудачное решение этой задачи может обнаружиться только на более поздних этапах конструирования (детальная проработка конструкции, испытание опытного образца и т. п.), что может привести к необходимости переработки всей конструкции, и, как следствие, увеличению затрат и сроков разработки РЭА.

На начальных этапах проектирования в распоряжении конструктора имеется техническое задание (ТЗ), в котором содержится следующая информация:

суммарная мощность тепловыделения в блоке: Ф;

диапазон возможного изменения температуры окружающей среды: t_{c max} , t_{c min};

пределы изменения давления окружающей среды: p_min , p_max;

время непрерывной работы прибора: _н;

допустимые температуры элементов: t_i;

коэффициент заполнения аппарата (не всегда):

K₃=V_i/V (1)

где V_i – объем i-го элемента РЭА; n – число элементов; V – объем, занимаемый РЭА.

Также могут задаваться горизонтальные (L₁, L₂) и вертикальные (L₃) размеры корпуса РЭА. Эти исходные данные недостаточны для детального анализа теплового режима РЭА, но их можно использовать для предварительной оценки и выбора системы охлаждения. Последний носит вероятностный характер, т. е. дает возможность оценить вероятность обеспечения заданного по ТЗ теплового режима РЭА при выбранном способе охлаждения. По результатам обработки статистических данных для реальных конструкций, тепловых расчетов и данных испытания макетов были построены графики (рисунок 2–4 /1/ стр. 120), характеризующие области целесообразного применения различных способов охлаждения. Эти графики построены для непрерывной работы РЭА и связывают два основных показателя: V_c=f(lgq).

Первый показатель Vc = t _{i min} -t_c – перегрев относительно окружающей среды t_c корпуса наименее теплостойкого элемента, для которого допустимая и приведенная в ТЗ температура t_imin имеет минимальное значение. Заметим, что для свободного охлаждения t_c = t_{c max}, т. е. соответствует максимальной температуре окружаю­щей среды по ТЗ; для принудительного охлаждения t_c = t_BX, т. е. cоответствует температуре воздуха (жидкости) на входе в РЭА. Второй показатель q равен плотности теплового потока, проходящего через условную площадь поверхности А_п теплообмена:

q = Фk_p/ A_n, А_п = (L₁L₂+(L₁+L₂)L₃K₃) (2)

где: Ф – суммарная мощность, рассеиваемая с этой поверхности;

k_p – коэффициент, учитывающий давление воздуха (при атмосферном давлении k_p = 1);

k_З – коэффициент заполнения, определяемый по формуле (1).

На рисунке представлены два типа областей: в одном можно рекомендовать примене­ние какого-либо одного способа охлаждения (не заштрихованы: 1– свободное воздушное, 3 – принудительное воздушное, 5 – принудительное испарительное); в другом возможно применение двух или трех способов охлаждения (заштрихованы: 2 – свободное и принудительное воздушное, 4 – принудительное воздушное и жидкостное, 6 – принудитель­ное жидкостное и свободное испарительное, 8 – свободное принудительное и свободное испарительное, 9 – свободное и принудительное испарительное).

Определим способ охлаждения блока в герметичном корпусе с исходными данными приведенными в задании на курсовую работу. Для этого произведем расчет по формуле (2) следующих величин:

V_c = 423– 293 = 103 ^оК

q = 80*1 / (0.6*0.14+(0.6+0.14)*0.05*0.25) = 930.23 Вт/м²

lg q = 2.65

Из рисунка 2–4 /1/ стр. 120 получим, что точка с заданными параметрами попадает в область 1, т. е. применяется свободное воздушное охлаждение.

3 Расчетная часть

3.1 Расчет теплового режима блока

3.1.1 Приближенная методика расчета теплового режима блока

Для герметичных аппаратов без стоков энергии расчет теплового режима можно упростить.

Первый шаг к упрощению методики расчета таких аппаратов это получение формул для расчета температур корпуса и зоны:

t_k = t_c + P ; t₃ = t_k + P . (3)

Из этих уравнений видно, что температура кожуха при заданном значении t_c однозначно определяется мощностью P и тепловой проводимостью _k:

t_k = t_k (t_c, P, _k); (4)

а температура tз является функцией:

t₃ = t₃ (t_k, P, ₃). (5)

Следовательно, при заданных значениях t_c, P и геометрических параметров аппарата намечается два этапа расчета: вначале рассчитывается температура кожуха, а затем по найденному значению t_k определяется температура t_з.

На основании (4) можно записать, что температура V_k перегрева кожуха является функцией следующих параметров:

_k = _k (P,L₁,L₂,h,t_c,,H); (6)

где P – давление.

Тепловая проводимость _k любого реального аппарата практически равна тепловой проводимости куба с равновеликой поверхностью. Следовательно, параметры L₁, L₂ и h можно заменить одним S_k (поверхностью кожуха), который однозначно определяется величину ребра куба с равновеликой поверхностью:

L = . (7)

Кроме того, вместо P в уравнение (6) можно ввести удельный тепловой поток P_{уд. к} с поверхности кожуха:

P_уд.к. = . (8)

После указанных замен можно написать, что температура _k равна:

_k = _k (P_уд.к.,S_k,t_c,,H). (9)

Связь между _k и определяющими ее параметрами будем искать в форме зависимости:

_k = _k0 (x = P_уд.к.,S_k,t_c,,H ); (10)

где:

K_x = ; (11)

_k0 = _k0 (P_уд.к0.,S_k0,t_c0,₀,H₀); (12)

здесь _k0 – температура кожуха при базовых значениях всех параметров;

_kx – значение температуры кожуха при базовых значениях всех параметров, кроме x. Индексом «0» снабжены базовые значения параметров.

Зависимости коэффициентов K_x от соответствующих параметров x можно представить в виде графиков, для получения которых необходимо найти отношение V_k / V_k0 при различных значениях выбранного x базовых (фиксированных) значениях всех остальных параметров.

Температура кожуха может быть определена по формуле:

_k = _PkK_SK_tK_K_H. (13)

После определения температуры кожуха можно переходить к определению перепада температур t_з.к между нагретой зоной и кожухом. В общем случае разность температур t_з.к является функцией теплового потока P, размеров кожуха L₁, L₂, h, его температуры t_к, размеров воздушных зазоров h₂ и h₂ с одной и другой стороны нагретой зоны, приведенной степени черноты _п и давления H.

При определении коэффициентов теплообмена между нагретой зоной и кожухом аппарата за определяющий размер шасси берется величина l= L₁ L₂, т. е. шасси в виде квад­ра­та, равновеликого по площади реальному шасси. Следовательно, при расчете t_з.к можно считать, что любой аппарат в плоскости, параллельной шасси, имеет квадратное сечение, и величину t_з.к можно представить в виде функции следующих параметров:

t_зх = f(P_уд.з., l,h,K₃ ,h₁/l, t_k,_п,H) (14)

где k_з – коэффициент заполнения аппарата, т. е. отношение реального объема нагретой зоны к полному объему аппарата.

Установив параметры, определяющие разность температур t_з.к, можно получить вспомогательные графики и рассчитать величину t_з.к по формуле, аналогичной (13):

t_зх = t_з K_lK_hK_K3K_h1/lK_HK_пK_tk (15)

3.1.2 Расчет теплового режима блока

Требуется рассчитать температуру t_з нагретой зоны аппарата с внешними размерами L₁ = 0.66 м, L₂ = 0.28 м и h = 0.15 м. Шасси расположено горизонтально в средней части аппарата и занимает все его сечение. Детали расположены сверху и снизу шасси равномерно, коэффициент заполнения k_з равен 0.25. Все поверхности имеют степень черноты 0.9. Давление снаружи аппарата 0.08 МПа, температура окружающей среды равна 20 °С. Мощность рассеиваемой аппаратом тепловой энергии 120 Вт.

1) Проведем вспомогательные расчеты:

S_k = 2(hL₂ + L₁h + L₂L₁) = 2*(0.15*0.28+0.66*0.15+0.28*0.66) = 0.651 м²;

P_уд.к = P/ S_k = 80 / 0.651 = 122 Вт/м²;

l = L₁ L₂ =  0.66*0.28 = 0.4 м;

h₃ = k₃h = 0.25*0.15 = 0.03 м;

h₁ = 0.5( h –h₃ )= 0.5*(0.15 – 0.03) = 0.06 м;

h₁ / l = 0.06 / 0.4 = 0.15

S₃=2(h₃L₂ + L₁h₃ + L₂L₁)=2*(0.03 *0.28+0.66*0.03+0.28*0.66) = 0.426 м²;

P_уд.3 = P/ S₃ =80 / 0.426 = 187,79 Вт/м²;

2) Рассчитаем температуру кожуха при P_уд.к =122 Вт/м²; t_c = 46° С;  =0.9; S_k = 0.651 м²; H = 753 мм рт. ст.

По графикам рисунок 5–4 /3/ стр. 164 определяем значения V_Pk и коэффициентов k_x:

V_Pk = 17 град; k_t = 1; k_ = 1; k_S = 1; k_H = 1

По формуле (13) находим температуру V_k перегрева кожуха над средой

V_k = 17*1*1*1*1 = 17 град

Температура кожуха t_k = t_c + V_k = 46 + 17 = 63 °С

3) Рассчитаем температуру зоны при P_уд.з = 187,79 Вт/м²; l = 0.4 м; k₃ = 0.25; h = 0.15 м; h₁/ l = 0.15; _п = 0,81; t_k = 63 °С; H =753 мм рт. ст.

По графикам 5–6 /3/ стр. 167 определяем значения t_з и коэффициентов K_x:

t_з = 17 град; k_k3 = 1; k_h = 1.01; k_h1/l = 1.05; k_l = 1.04; k_п= 0.98; k_tk = 1.02; k_H = 1.

По формуле (15) находим разность t_з температур между нагретой зоной и кожухом:

t_з.к = 17*1*1.01*1.05*1.04*0.98*1.02*1 = 17.2 град

Температура нагретой зоны:

t_з = t_к + t_з.к = 63 + 17.2 = 80.2 °С

3.2 Выбор конструкции и расчет параметров радиатора для элемента с наиболее тяжелым тепловым режимом

3.2.1 Эффективный коэффициент теплоотдачи радиатора

Для системы воздушного охлаждения широкое применение получили радиаторы, которые различаются по виду развитой площади поверхности, а именно: пластинчатые, ребристые, игольчато-штыревые, типа «краб», жалюзийные, петельно-проволочные.

Исследования теплообмена радиаторов различного типа позволили построить приближенную зависимость среднего перегрева V_s = t_s-t_c основания площадью A от удельной нагрузки q = Ф/ A (A=L₁L₂, A=D²/4) при свободной и вынужденной вентиляции. Этот график приведен в приложении Б.5 /1/ и позволяет остановиться на том или ином типе радиатора, если заданы поверхностная плотность теплового потока q и допустимый перегрев V_s основания.

Для характеристики теплообменных свойств радиатора используют следующие параметры: эффективный коэффициент теплоотдачи _эф, тепловую проводимость _, тепловое сопротивление R_. Эти параметры связаны со средним перегревом V_s основания и рассеиваемым потоком Ф зависимостями:

_эфA=_ =R^-1_ , A=L₁L₂ , A = D²/4 , Ф = __s = R^-1__s = _эф _s A (16)

где L₁, L₂ – размеры основания прямоугольного радиатора;

D – диаметр круглого основания.

Формула (16) справедлива для радиатора любого из рассмотренных выше типов; вся сложность процессов переноса теплоты и конструктивные особенности сосредоточены здесь в одной величине – эффективном коэффициенте теплоотдачи. Последний может быть определен экспериментально или расчетным путем. В первом случае в основу положена зависимость (16), позволяющая по найденным из опыта значениям Ф и V_s определить _эф . В приложении Б.5 /1/ приведены полученные таким способом зависимости для различных типов выпускаемых промышленностью радиаторов. С помощью этих графиков можно подобрать радиатор, средняя температура основания которого не превышает заданной величины.

Рассмотрим теперь на примере пластинчатых, ребристых и игольчато-штыревых конструкций радиаторов расчетный метод определения параметров _эф, _ или R_. Необходимость анализа процесса теплообмена радиаторов связана с непрерывным изменением выпускаемых промышленностью типоразмеров радиаторов. Представим тепловую модель одиночного ребра или штыря в виде стержня произвольного сечения f с периметром U и длиной h, находящегося в среде с температурой t_c и коэффициентом теплоотдачи с боковой поверхности . Перегрев х_i торца стержня i, в который входит поток Фi определяется по формуле:

_i = [ Ф_i/ (fb)]ctgbh` , b<sup>2</sup> = U/(f) , h` = h + f/U. (17)

Тепловое сопротивление R_i одиночного стержня на основании этой зависимости и формулы (16):

R_i = _I^-1 = v_i / Ф_i = ctgbh`/ (fb). (18)

Общая проводимость _р оребренной части радиатора равна сумме проводимостей _i всех N ребер:

_р = = N_i. (19)

Если проводимость от неоребренной части радиатора равна _Hр , то общая проводимость радиатора:

_ = _нр + Nfb_thb_h`. (20)

Параметр b содержит коэффициент теплоотдачи боковой поверхности ребра или штыря, который определяется из соответствующих критериальных уравнений. В частности, для вынужденной конвекции воздушной среды может быть рекомендована формула:

N_u = L/_в = 0,21 Re^0,8 , Nu = L/_в , Re = _pL/v_в (21)

где _в , _в – теплопроводность и кинематическая вязкость воздуха при средних значениях температур;

L – определяющий размер для данного вида оребрения;

_p– расчетная скорость движения воздуха для данного вида оребрения.

Особенности теплообмена радиатора учтены выборе параметров L и _p, которые равны для ребристых поверхностей _p = 1,25, L = L₁ , для игольчато-штыревых радиаторов L = d, _p = S_ш/( S_ш - d), где – средняя скорость движения воздуха; S_ш – шаг оребрения; d – диа­метр штыря.


3.2.2 Методика выбора и расчета радиатора

На рисунке 1 схематически изображен радиатор 1 с закрепленным на нем прибором 2, внутри которого имеются источники мощностью Ф, разогревающие рабочую область прибора и его корпус до температур t_р и t_к; в месте крепления прибора к радиатору температура основания радиатора t_и , а средняя температура основания радиатора t_s.

Приведем исходную информацию, которая должна быть при проектировании или выборе радиатора: предельно допустимая температура рабочей области прибора (t_р)_доп или его корпуса (t_к)_доп; рассеваемая прибором мощность Ф; температура t_с окружающей среды или набегающего потока; внутреннее тепловое сопротивление R_вн прибора между рабочей областью и корпусом; способ крепления прибора к радиатору, который характеризуется тепловым сопротивлением R_к контакта. Проектируемый радиатор должен удовлетворять некоторым дополнительным требованиям: иметь малую массу и габариты, выполнять свои функции при наименьшем расходе воздуха, если требуется принудительное охлаждение.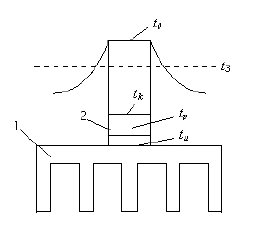



Рисунок 1 – Температурное поле радиатора и прибора
На рисунке 1 представлена схема соединения тепловых сопротивлений между рабочей областью и окружающей средой, из которой следует:

t_p – t_c = (t_p - t_k)+(t_k -t_и)+(t_и-t_c); (22)

t_и-t_c = (t_p – t_c) – Ф(R_вн + R_k).

Введем безразмерную величину в, связывающую среднюю температуру t_s основания радиатора и температуру t_и в месте крепления прибора к радиатору:

 = (t_и - t_c)/(t_s - t_c) = f(B, ); (23)

она зависит, как показано в приложении Б.2 /1/, от двух чисел подобия:

B = (₁ + ₂)A_p / () и (24)

где: ₁ и ₂ – коэффициенты теплоотдачи с одной и другой сторон радиатора;

A_р , A_и – площади оснований радиатора и прибора;

 - толщина основания радиатора;

 - теплопроводность материала радиатора.

Функциональная зависимость (23) может быть найдена для любого положения источника на радиаторе и любых значений его размеров. Из формул (22) и (23) получаем:

t_s – t_c = [(t_p - t_c) – Ф(R_вн –R_K)]/. (25)

Все параметры, входящие в квадратные скобки формулы (25), заданы, а параметры (t_s – t_с) и  неизвестны. Дальнейший подбор радиатора может быть осуществлен с помощью формул (16), (25) и графиков, представленных на рисунках Б.8 – Б.12 /1/ на основе метода последовательных приближений. В первом приближении задают значение ¹ = 1,2 и по формуле (25) определяют (t_s – t_c), затем в первом приближении задают площадь A_р основания радиатора и по графикам рисунок Б.12 /1/ подбирают вид оребрения и характер теплообмена (свободная или вынужденная конвекция). Зная Ф, A_р и (t_s – t_c), по формуле (16) находят в первом приближении эффективный коэффициент теплоотдачи _эф.

По графикам, представленным на рисунке Б.8 – Б.11 /1/, уточняют геометрические размеры параметры радиатора, после чего переходят ко второму приближению расчетов, а именно: находят безразмерные числа B = _эф A_p / () и по графику рисунок Б.3 /1/ опре­деляют ^II и уточняют по формуле (23) значение (t_s – t_с).
3.2.3 Выбор конструкции и расчет параметров радиатора

Требуется подобрать радиатор для охлаждения транзистора KT805, рассеивающего мощность Ф = 15 Вт и находящегося внутри блока. Контакт транзистора с радиатором осуществлен по площади A_и = 0.00024 м²; внутреннее тепловое сопротивление прибора R_вн = 1.2 °К/Вт, тепловое сопротивление контакта R_к = 2 °К/Вт, допустимая температура кол­ле­к­торного перехода в транзисторе t_рдоп = 150 °С; допустимая температура корпуса в транзисторе t_кдоп = 125 °С; условия теплообмена – свободная конвекция, температура воздуха в блоке t_с = 46 °С.

1) По формуле (25) определяем температуру t_и в месте крепления транзистора:

(t_и - t_c) = (125 – 46) – 15*(1,2 + 2) = 31 °С.

2) В первом приближении принимаем ^I = 1.2 и из (23) находим

(t_s - t_c)¹ = 31/1.2 = 25.8 °С.

3) Задаем для простоты в первом приближении площадь A_р основа­ния; пусть A_р = 0.66*0.28 = 0.1848 м². Тогда плотность теплового потока:

q = 15 / 0.1848 = 81 Вт/м².

4) По графику, приведенному на рисунке Б.12 /1/ для (t_s – t_с)¹ = 31 °С и q = 329 Вт/м², определяем возможный вид оребрения радиатора в условиях свободной конвекции; как следует из графиков, необходимо выбрать пластинчатый радиатор.

5) По формуле (16) определяем коэффициент эффективной теплоотдачи, необходимый для обеспечения заданного теплового режима. По графикам, представленным на рисунке Б.8 /1/, наиболее близкий профиль оребрения штыревого радиатора соответствует h₁ = 20 мм, S_ш = 7 мм, d = 2 мм, для которого _эф = 65 Вт/( м²·К).

6) Находим по формулам (24) второе приближение ^II, полагая _эф, а также выбирая материал радиатора, например дюралюминий  = 180 Вт/(м·К):

B = 65*0.1848/ (180*2,5*10^-3) = 5.4;

A_и / A_р = 0.001848 / 0.1848 = 0.01.

По графику рисунок Б.3 /1/ находим ^II = 1.7 и уточняем по формуле (23) перегрев:

(t_s – t_с)^II =31/ 1.7 = 18.2 °С.

7) Уточняем размеры основания и тип радиатора. Согласно графику, приведенному на рисунке Б.12 /1/, для (t_s – t_с)¹ = 31 °С и q = 329 Вт/м² тип радиатора остается прежним. Таким образом, окончательно останавливаемся на радиаторе штыревого типа из дюралюминия с площадью основания A =0.1848 м² (L₁ = 660 L₂ = 280 мм), h = 20 мм, S_ш = 7 мм, d = 2 мм, эскиз которого приведен на рисунке 2.



Рисунок 2 – Эскиз радиатор

Заключение
В результате выполнения курсовой работы в качестве системы охлаждения блока было выбрано свободное воздушное охлаждение. Для данной системы охлаждения был произведен расчет теплового режима блока и получены следующие результаты: температура корпуса блока составила t_k = 63 °С, температура нагретой зоны t_з = 80.2 °С. Погрешность расчета теплового режима аппарата по приближенной методике составляет 25% по отношению к эксперементу. Для наиболее теплонагруженного транзистора КТ805 произведен расчет радиатора. В результате чего был получен радиатор штыревого типа из дюралюминия с площадью основания A =0.1848 м² (L1 = 660 L2 = 280 мм), h = 20 мм, S_ш = 7 мм, d = 2 мм.

Список литературы
1 Ашков Е.М. Теплофизическое проектирование современных радиоэлектронных средств: Учеб. пособие / Е.М. Ашков, А.В. Муратов. Воронеж: ВГТУ, 2001. 132с.

2 Дульнев Г. Н., Парфенов В. Г., Сигалов А. В. Методы расчета теплового режима приборов. М.: Радио и связь, 1990. – 312 с.

3 Дульнев Г. Н., Семяшкин Э. М. Теплообмен в радиоэлектронных аппаратах. Л.: Энергия, 1968. – 360 с.

4 Стандарт предприятия: Курсовое проектирование. Организация, порядок проведения, оформление расчетно-пояснительной записки и графической части. Воронеж: ВГТУ, 1998.48с. (№186-98).