Переходные процессы в системах электроснабжения. Переходные процессы 1 страницу. Курсовой проект по электромеханическим переходным процессам

Название	Курсовой проект по электромеханическим переходным процессам
Анкор	Переходные процессы в системах электроснабжения
Дата	15.03.2022
Размер	4.81 Mb.
Формат файла
Имя файла	Переходные процессы 1 страницу.docx
Тип	Курсовой проект #398033

Липецкий государственный технический университет

Факультет автоматизации и информатики

Кафедра электрооборудования

КУРСОВОЙ ПРОЕКТ

по электромеханическим переходным процессам

Расчет переходных режимов и анализ устойчивости системы электроснабжения крупного промышленного предприятия

Вариант №8 (6)

Студент

Группа М-ЭО-20 _______________________ Павлов И.В.

Руководитель

к.т.н., доцент _____________________________ Зацепин Е.П.

Липецк, 2021

Аннотация

С. 50. Ил. 35 Табл. 6 Литература 3 назв. Прил.

В представленном курсовом проекте рассматривается система электроснабжения некоторого обобщенного крупного промышленного предприятия. По заданию на одной из линий происходит двухфазное короткое замыкание на землю, в связи с которым студенту необходимо рассчитать начальную стадию возникающего в связи с этим коротким замыканием переходного процесса в точке возникновения несимметрии, так же в сечении, удаленном от места аварии.

Во второй и третьей частях работы выполняется расчет соответственно статической и динамической устойчивости рассматриваемой системы электроснабжения.

Аннотация 2

Оглавление 3

Задание на курсовой проект 4

1 Расчет начальной стадии переходного процесса при несимметричном коротком замыкании в относительных единицах 8

1.1 Составление схем замещения системы прямой, обратной и нулевой последовательности 8

1.2 Определение параметров элементов схем замещения 10

1.3 Преобразование схем замещения к простейшему виду 15

1.4 Определение токов и напряжений всех последовательностей в точке короткого замыкания. Построение векторных диаграмм 20

1.5 Определение токов и напряжений 24

2 Расчет предела статической устойчивости станции системы электроснабжения предприятия 31

2.1 Составление схемы замещения. Расчет собственных и взаимных проводимостей схемы для узлов станции и системы 31

2.2 Построение угловой характеристики 34

2.3 Расчет запаса статической устойчивости 35

3 Расчет динамической устойчивости системы 36

3.1 Построение угловых характеристик для нормального, аварийного и послеаварийного режимов 36

3.2 Определение предельного угла отключения 42

3.3 Решение уравнение движения ротора генератора 43

Заключение 47

Список литературы 48

Задание на курсовой проект

1 Расчет начальной стадии переходного процесса при несимметричном коротком замыкании в относительных единицах:

1.1. Составить схемы замещения системы прямой, обратной и нулевой последовательности. Определить параметры их элементов в относительных единицах с приближенным приведением параметров схемы к основной ступени напряжения. Преобразовать каждую из трех схем замещения к простейшему виду.

1.2. Составить эквивалентную схему прямой последовательности. Определить токи и напряжения всех трех последовательностей в месте повреждения и в заданном сечении. Построить векторную диаграмму токов и напряжений. Определить п ней начальные действующие значения фазных токов и напряжений в месте короткого замыкания (принужденных составляющих) как в относительных, так и в именованных единицах. Сопоставить векторные диаграммы для места короткого замыкания и заданного расчетного сечения схемы. Сделать выводы.

2. Расчет предела статической устойчивости станции системы электроснабжения предприятия:

2.1. Составить схему замещения для анализа статической устойчивости станции. Для этого в схеме системы электроснабжения прямой последовательности нагрузку представить постоянным сопротивлением, а генератор – его переходными параметрами, учитывающими влияние АРВ пропорционального действия. Рассчитать собственные и взаимные проводимости схемы для узлов станции и системы.

2.2. Построить угловую характеристику активной мощности станции и выявить на ней предел статической устойчивости.

2.3. Рассчитать запас статической устойчивости для номинального режима работы станции и сравнить его с нормативным. Сделать вывод.

3. Расчет динамической устойчивости системы:

3.1. В качестве возмущающего воздействия принять рассчитанное в разделе 1 короткое замыкание на одной из цепей воздушной линии с последующим отключением поврежденной цепи с заданным временем t_отк. При этом для имеющих место трех режимов системы электроснабжения: нормального, аварийного (режим короткого замыкания) и послеаварийного (с отключением поврежденной цепи воздушной линии) – построить соответствующие схемы замещения и определить по ним собственные и взаимные проводимости для узлов станции и системы. Построить для рассматриваемых режимов системы электроснабжения угловые характеристики активной мощности станции. Генератор во всех режимах представляется приближенно – переходными параметрами с неизменной эдс E₀^′.

3.2. По построенным угловым характеристикам графически, уравнивая площадки ускорения и торможения, определить предельный угол отключения короткого замыкания (если он существует).

3.3. Методом последовательных интервалов решить уравнение движения ротора генератора в режиме короткого замыкания, построить график изменения во времени угла положения ротора генератора, по которому, зная предельный угол отключения, определить предельное время отключения короткого замыкания. Сопоставить его с заданным временем отключения и сделать вывод об устойчивости системы при заданным возмущении.

Если предельного угла отключения не существует, то объяснить физический смысл такого явления и проиллюстрировать его графиком изменения угла положения ротора генератора в режиме короткого замыкания.

Исходная схема исследуемой системы электроснабжения представлена на рисунке 1, а данные для расчетов представлены в таблицах 1 и 2 согласно заданному варианту и последней цифрой зачетной книжке.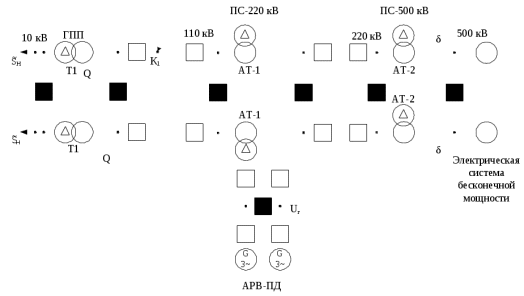

Рисунок 1 – Схема исследуемой системы электроснабжения
Таблица 1 – Параметры элементов схемы системы электроснабжения

Генератор электрической станции

ЭЭС

АТ–1

АТ–2

Т1

ВЛ –110кВ

ВЛ –220кВ

Нагрузка

P_н

cosφ_н

U_н

x^′′_d

x^′_d

x₂

T_j

I_с⁽³⁾

S_н

длина

P_н

cosφ_н

МВт

–

кВ

о.е.

кА

МВА

км

МВт

–

200

0,85

15,75

0,182

0,272

0,224

7,0

400

250

221

25,2

0,9

Таблица 2 – Параметры аварийного и послеаварийного режима

Точка и расчетный вид КЗ	Время отключения КЗ, с	Сечение расчетной схемы	Характеристики системы грозозащиты воздушных линий			Режим заземлителя Q в нейтрали Т1
			ВЛ – 110 кВ	ВЛ – 220 кВ
К1, (1,1)	0,24	γ-γ	Стальн. трос заземл.	Пров. трос изолир.	отключен

1 Расчет начальной стадии переходного процесса при несимметричном коротком замыкании в относительных единицах

1.1 Составление схем замещения системы прямой, обратной и нулевой последовательности

Прежде, чем составить схемы замещения прямой, обратной и нулевой последовательности, составляется расчетная схема, в которой указываются только те элементы, по которым возможно протекание аварийных токов или их составляющих. С учетом заданного варианта, составим расчетную схему и представим ее на рисунке 2.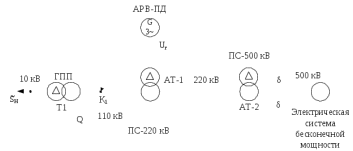

Рисунок 2 – Расчетная схема исследуемой системы
Схема замещения прямой последовательности соответствует обычной схеме, используемой для расчета любого симметричного трехфазного режима. Генераторы и нагрузки вводятся в нее соответствующими реактивностями и эдс (X^′′ и E^′′). Все остальные элементы входят в схему замещения неизменными во времени сопротивлениями. Схема замещения прямой последовательности для заданного варианта представлена на рисунке 3.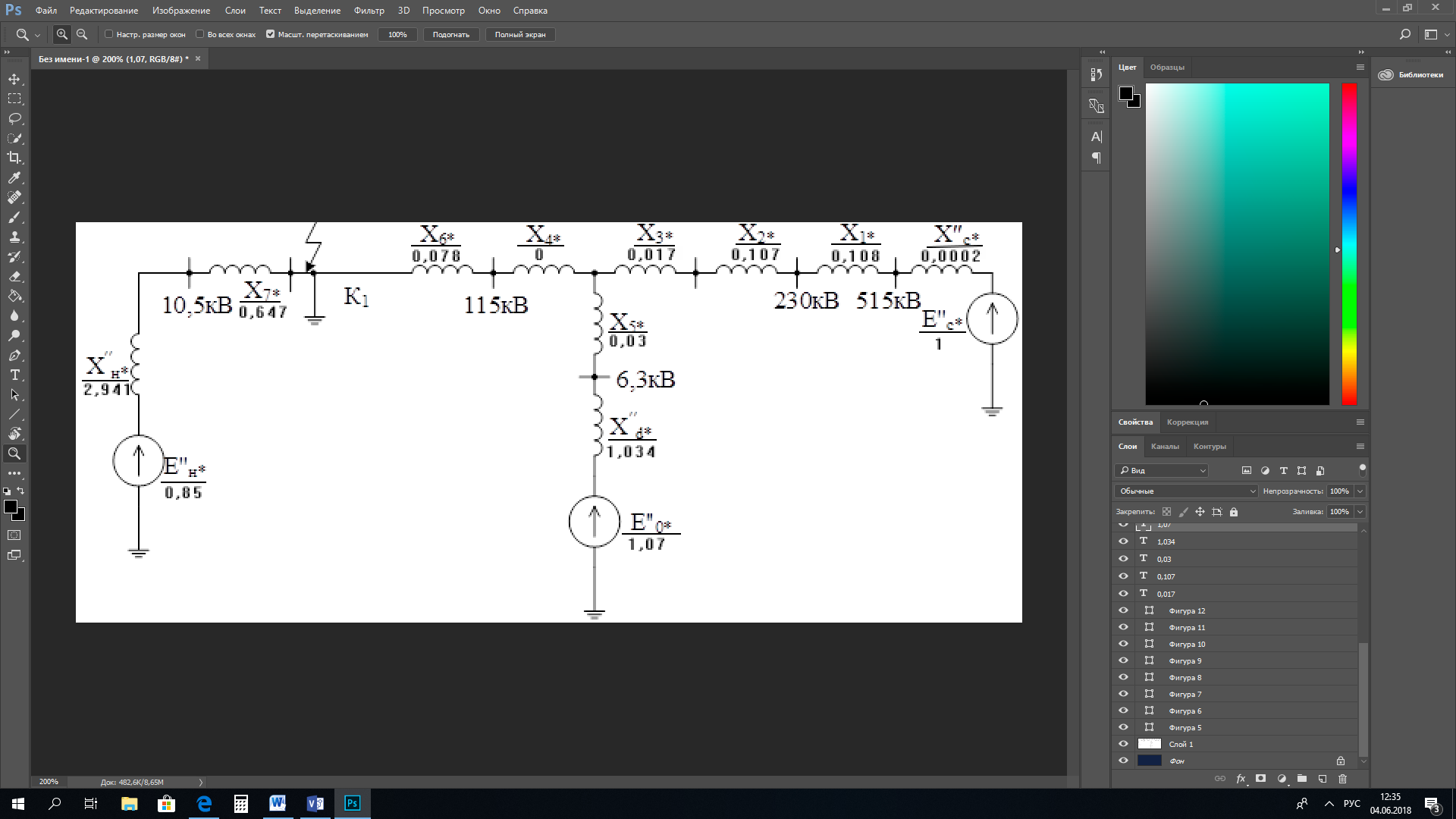

Рисунок 3 – Схема замещения прямой последовательности
Схема замещения обратной последовательности по структуре аналогична схеме замещения прямой последовательности, но отличие состоит в отсутствие эдс всех генерирующих устройств. Схема замещения обратной последовательности для заданного варианта представлена на рисунке 4.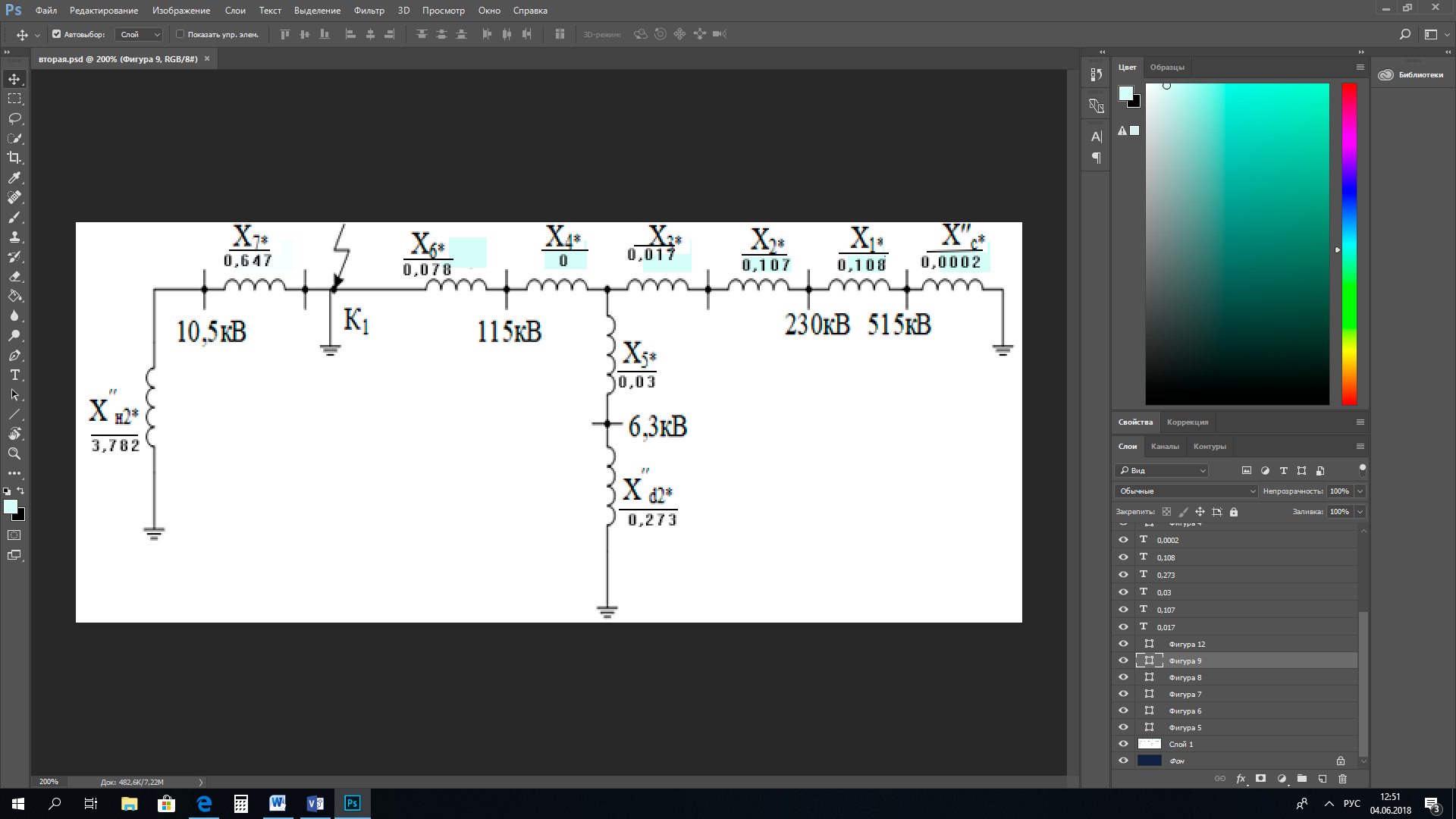

Рисунок 4 – Схема замещения обратной последовательности
Схема замещения нулевой последовательности в значительной мере определяется соединением обмоток входящих в нее трансформаторов и автотрансформаторов. Для циркуляции токов нулевой последовательности необходима по меньшей мере одна заземленная нейтраль. В схему замещения нулевой последовательности войдут только лишь те элементы схемы, через которые протекают токи нулевой последовательности. Сопротивления элементов в схеме нулевой последовательности в общем случае существенно отличаются от их сопротивлений в схемах прямой и обратной последовательностей. Схема замещения для заданного варианта представлена на рисунке 5.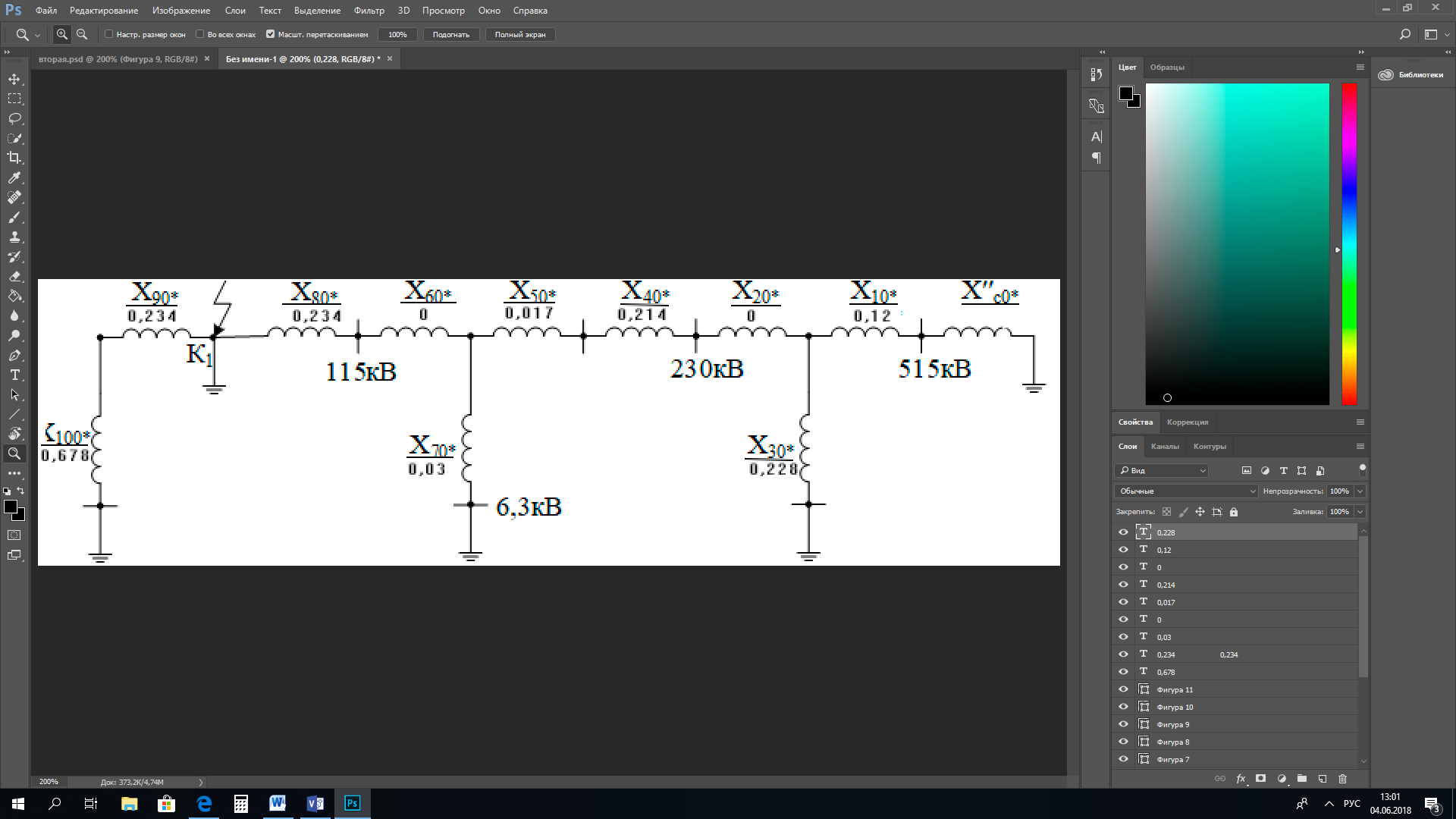

Рисунок 5 – Схема замещения нулевой последовательности

1.2 Определение параметров элементов схем замещения

Расчет выполним в относительных единицах с приближенным приведением параметров к основной ступени напряжения. Для этого выберем базисную мощность, равную номинальной мощности генератора: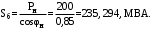

На рисунках 3, 4 уже заранее были расставлены напряжения ступеней. В качестве базисного напряжения выберем напряжение ВЛ – 110 кВ, на котором произошло короткое замыкание, то есть U_б1 = 115 кВ. Тогда остальные напряжения с учетом выбранного базисного напряжения будут иметь следующий вид: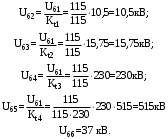

Рассчитаем сопротивления элементов схемы замещения прямой последовательности:

Сверхпереходное сопротивление системы: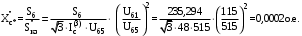

Сопротивление трансформатора АТ-2: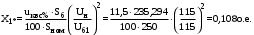

Сопротивление ВЛ – 220 кВ: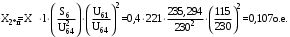

Напряжения короткого замыкания автотрансформатора АТ – 1: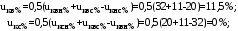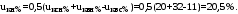

Сопротивления автотрансформатора АТ – 1: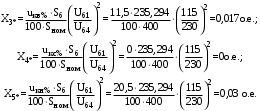

Сверхпереходное сопротивление генератора: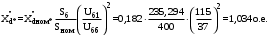

Сопротивление третьей части ВЛ – 110 кВ: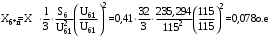

Сопротивление трансформатора Т1: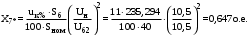

Сверхпереходное сопротивление нагрузки: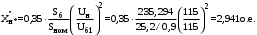

ЭДС системы, нагрузки и генератора: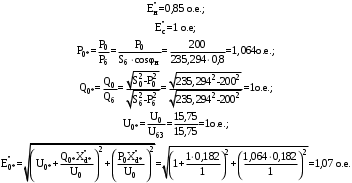

Сопротивления элементов схемы замещения обратной последовательности будут аналогичными сопротивлениям элементов схемы замещения прямой последовательности, кроме сопротивлений нагрузки и генератора, которые будут равны: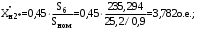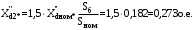

В схеме замещения нулевой последовательности требуется пересчет некоторых элементов относительно схемы замещения прямой последовательности:

Сопротивление системы: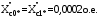

Напряжения короткого замыкания автотрансформатора АТ – 2: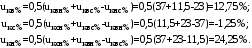

Сопротивления автотрансформатора АТ – 2: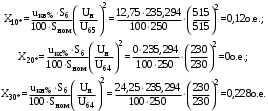

Сопротивление ВЛ – 220 кВ: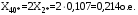

Сопротивления автотрансформатора АТ – 1: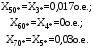

Сопротивление ВЛ – 110 кВ: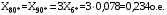

Сопротивление трансформатора Т – 1: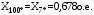

1.3 Преобразование схем замещения к простейшему виду

Посчитаем эквивалентные сопротивления для схемы замещения прямой последовательности: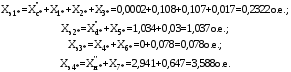

Тогда схема замещения примет упрощенный вид, представленный на рисунке 6.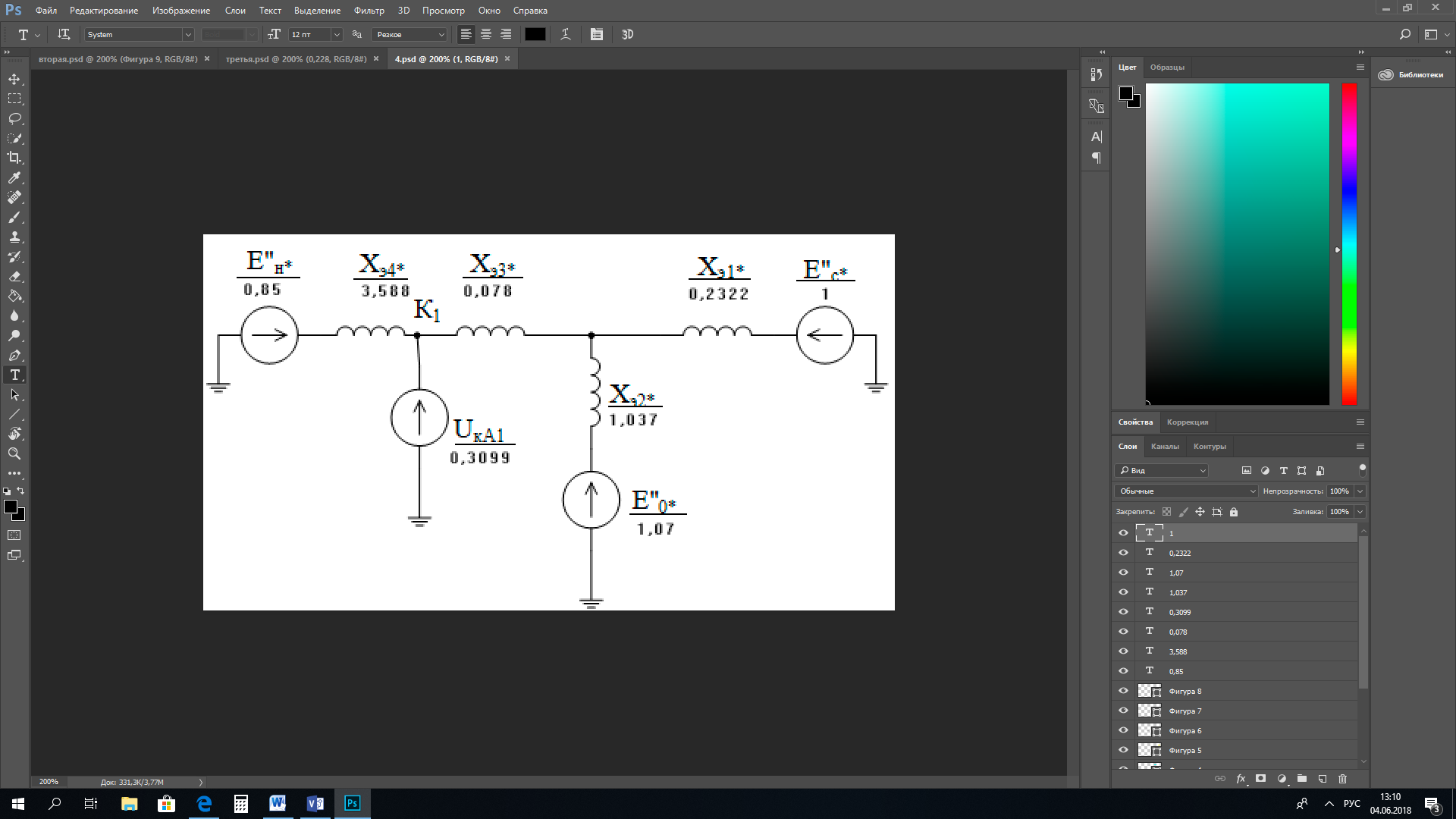

Рисунок 6 – Упрощенная схема замещения прямой последовательности
Продолжим упрощение схемы. Преобразуем ветви с эдс и сопротивлениями системы и генератора: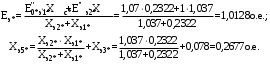

С учетом вышеизложенного, схема примет вид.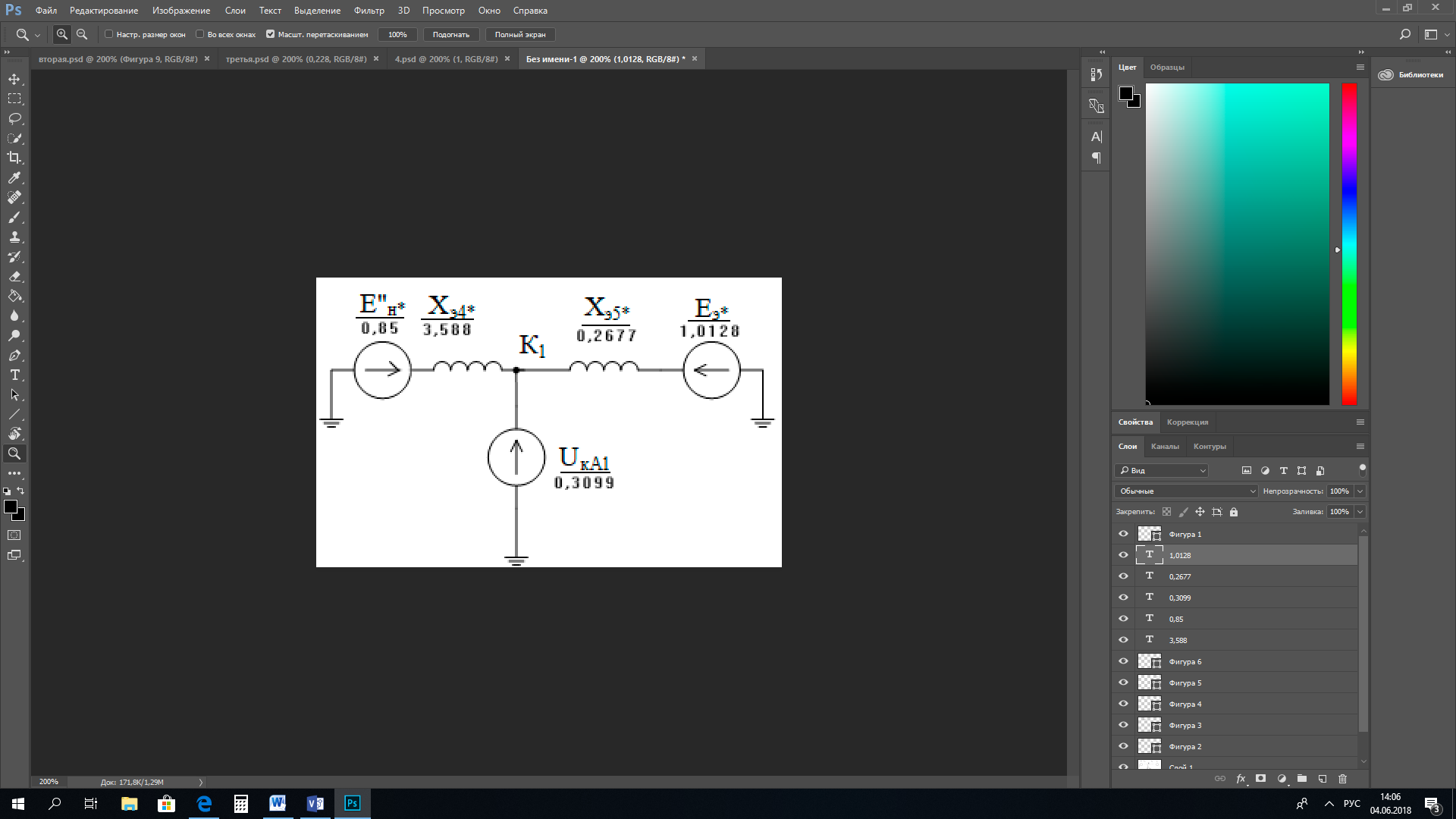

Рисунок 7 – Промежуточная схема замещения прямой последовательности
Проведем еще ряд преобразований: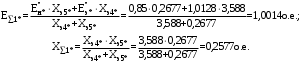

Схема замещения прямой последовательности примет простейший вид, представленный на рисунке 8.

Приступим к упрощению схемы замещения обратной последовательности. Для этого пересчитаем эквивалентные сопротивления из схемы замещения прямой последовательности: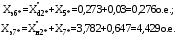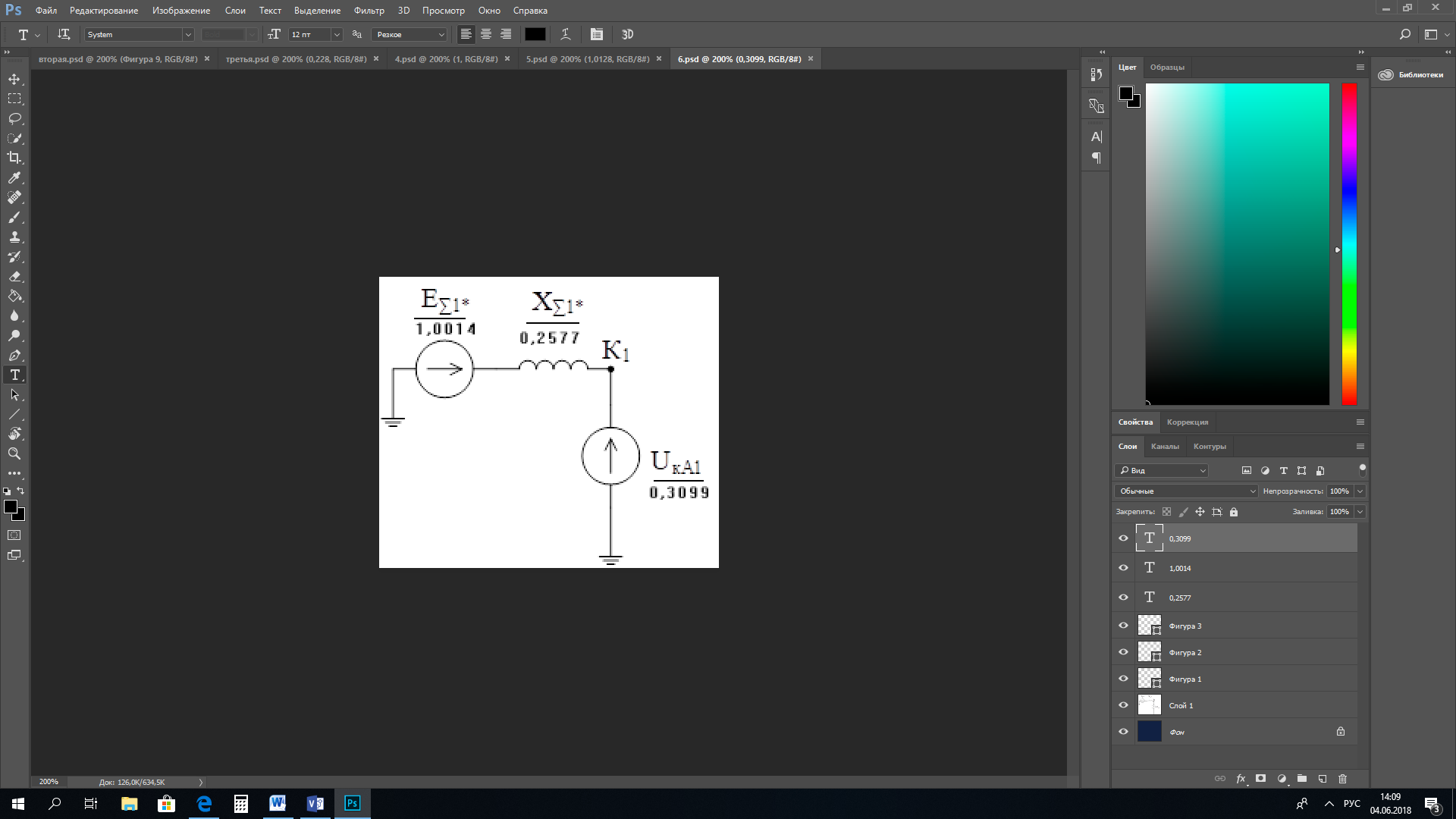

Рисунок 8 – Простейшая схема замещения прямой последовательности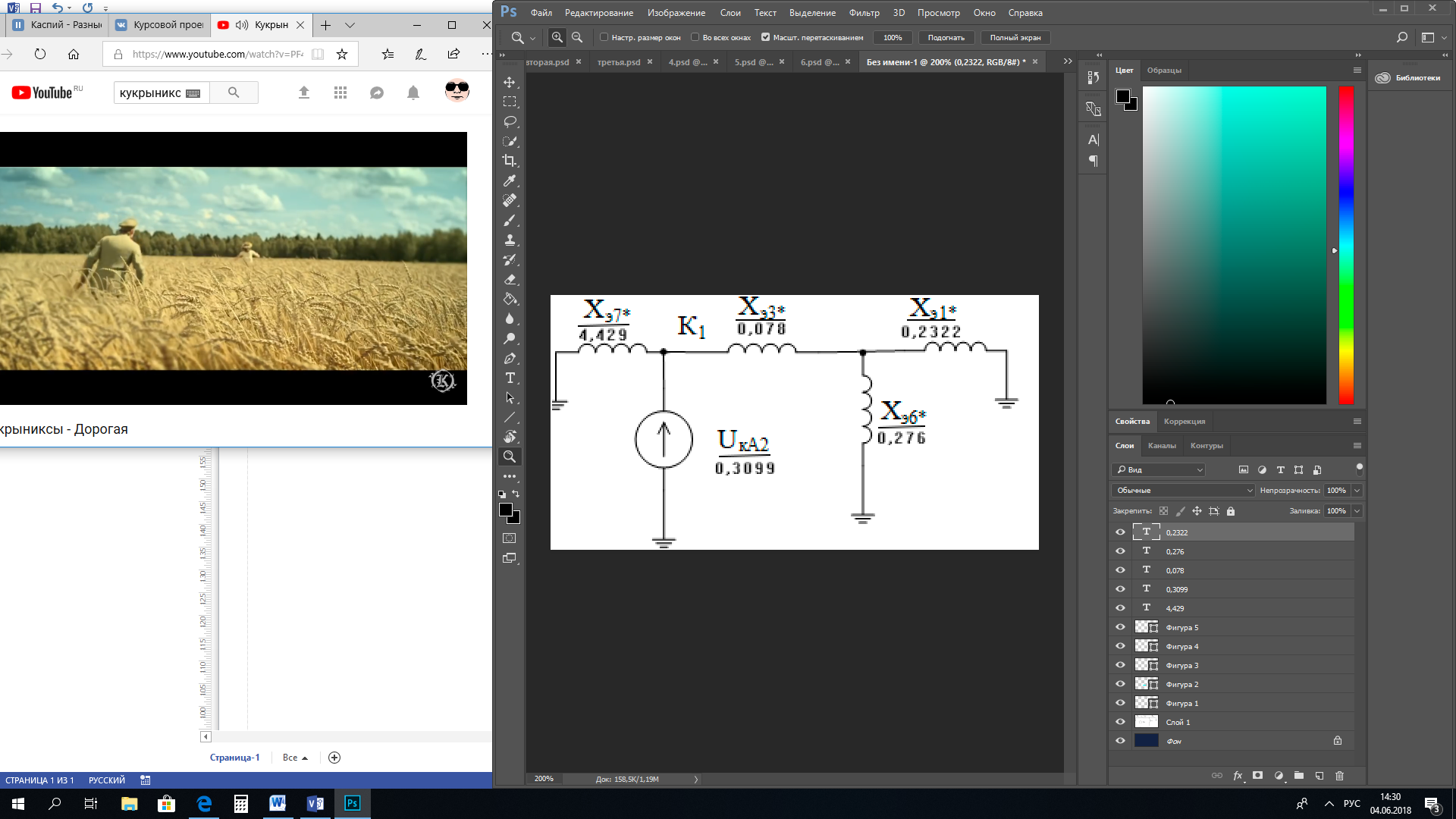

Рисунок 9 – Упрощенная схема замещения обратной последовательности
Вычислим эквивалентное сопротивление обратной последовательности: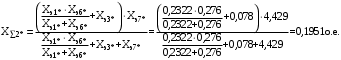

Получим простейшую схему замещения обратной последовательности и представим ее на рисунке 10.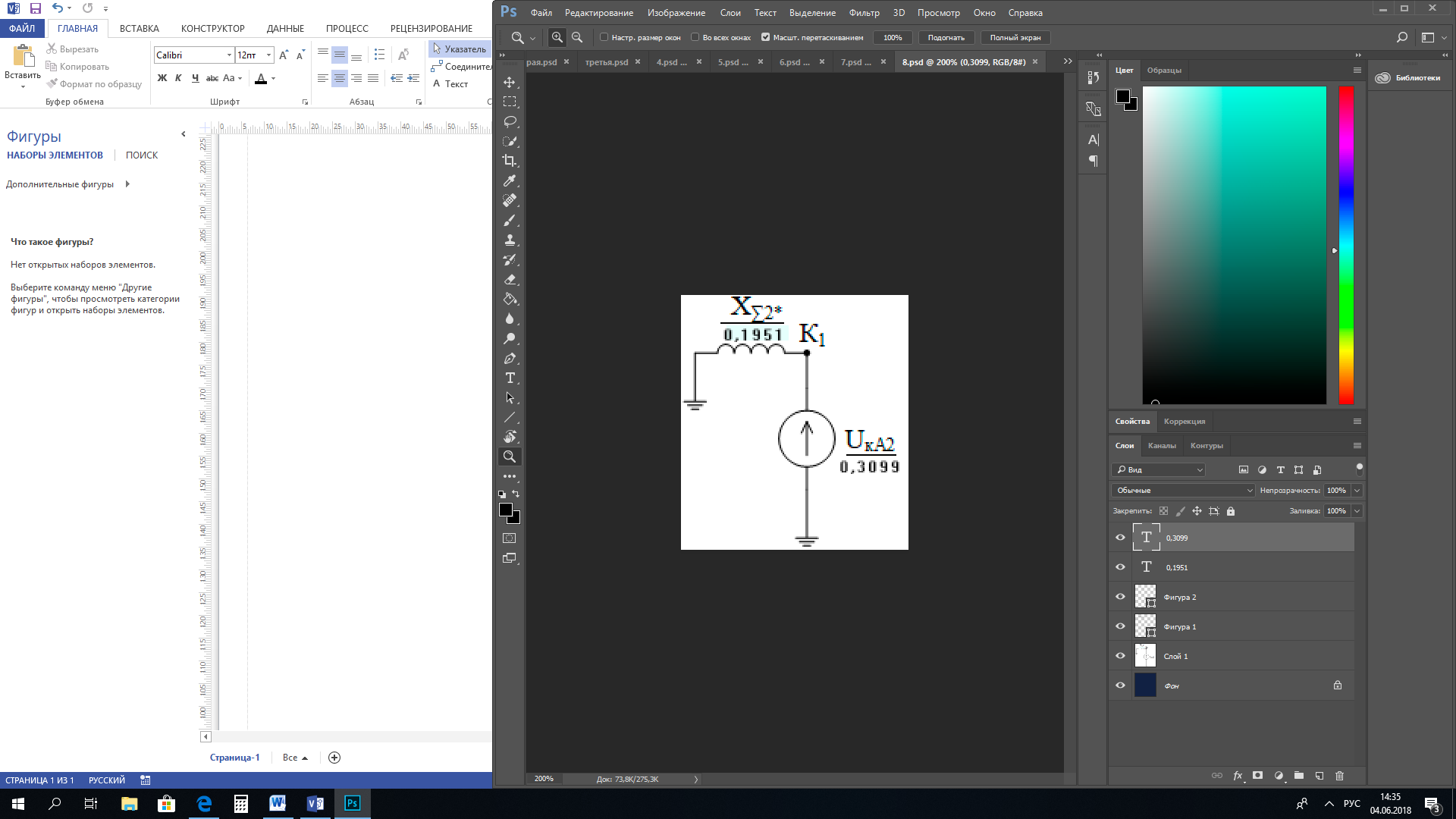

Рисунок 10 – Простейшая схема замещения обратной последовательности
Приступим к упрощению схемы замещения нулевой последовательности. Вычислим эквивалентные сопротивления: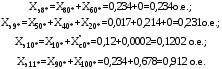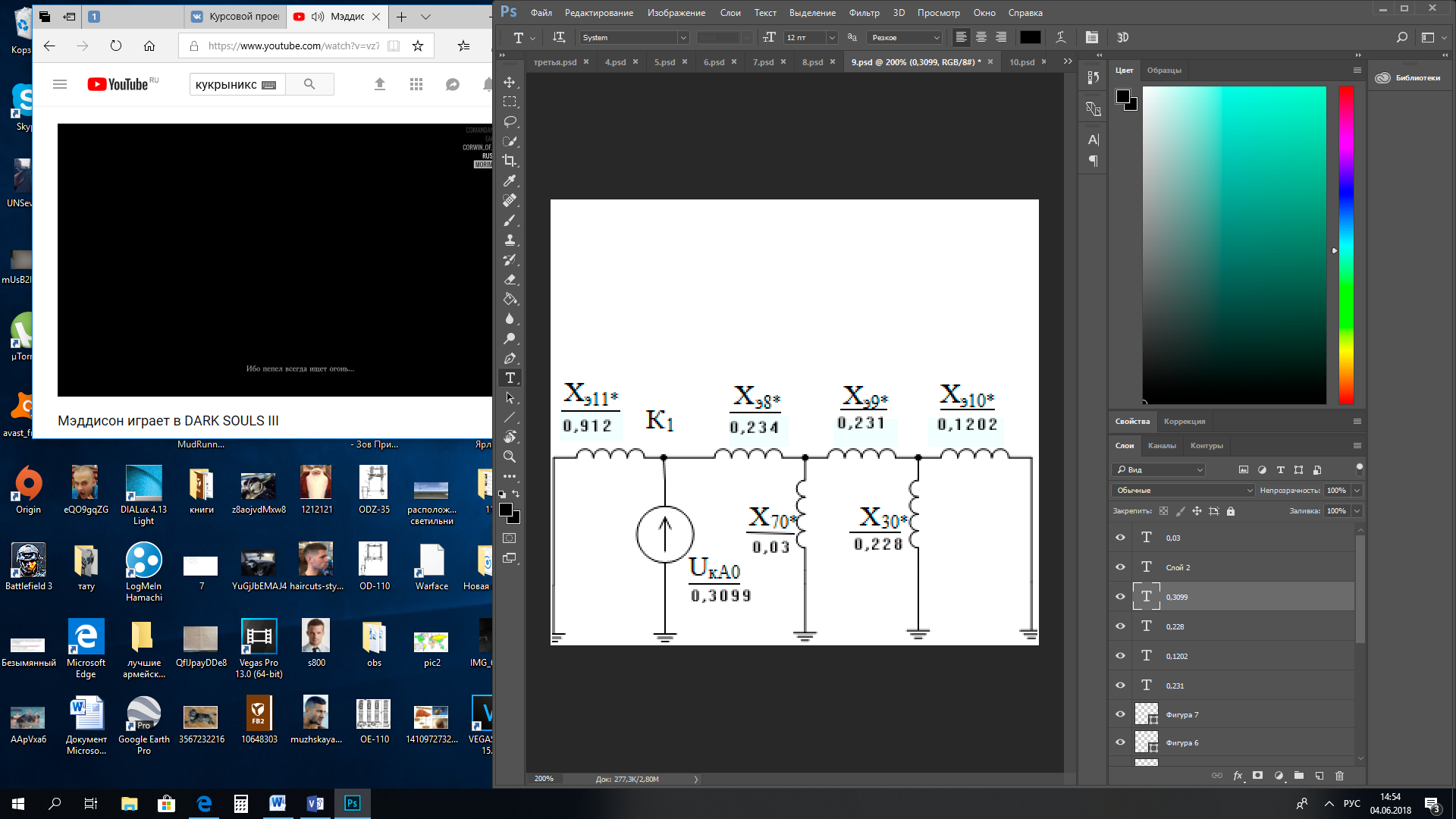

Рисунок 11 – Упрощенная схема замещения нулевой последовательности
Вычислим эквивалентное сопротивление нулевой последовательности: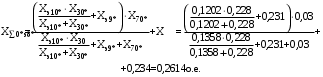

Получим простейшую схему замещения нулевой последовательности и представим ее на рисунке 12.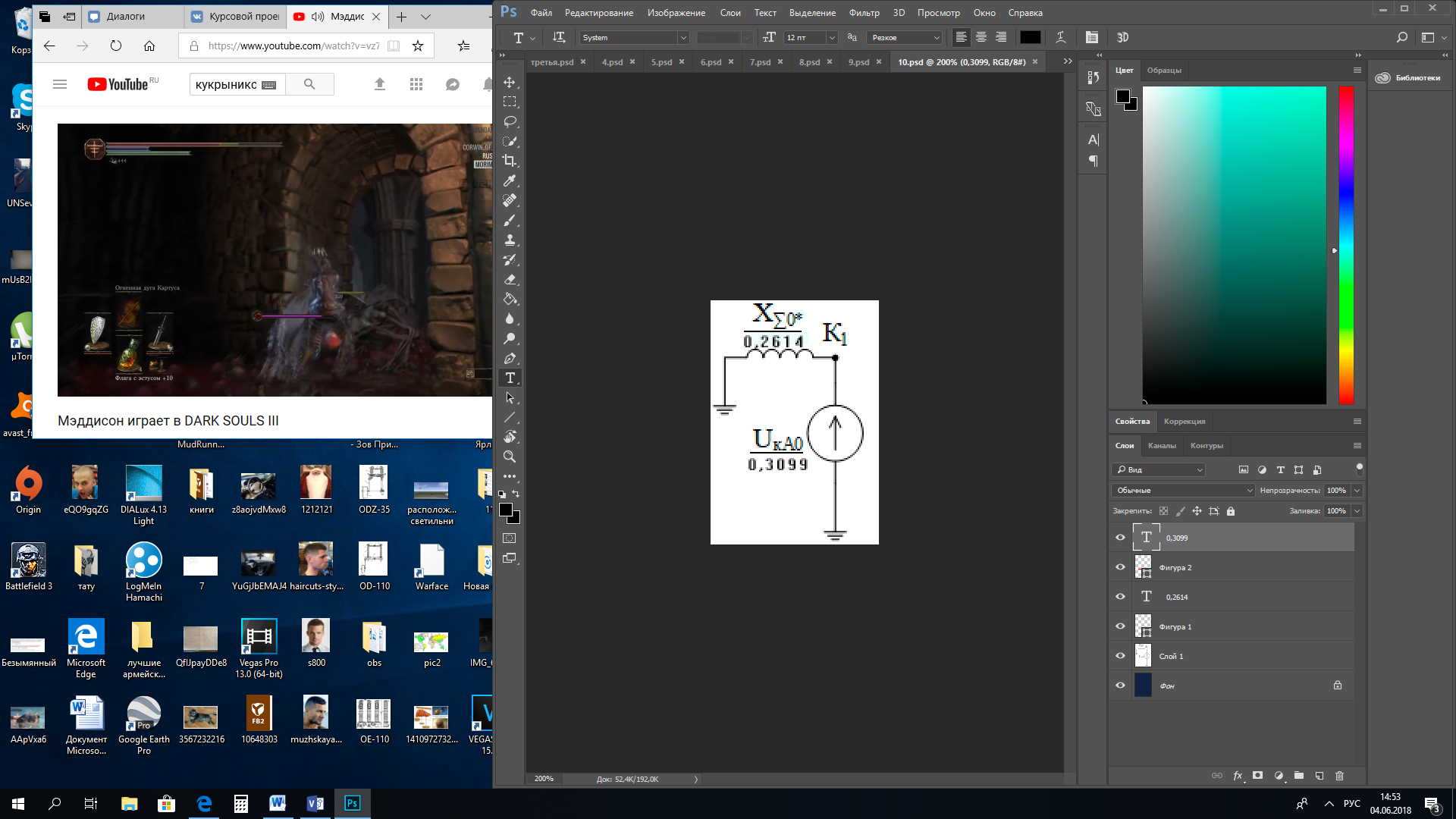

Рисунок 12 – Простейшая схема замещения нулевой последовательности

1.4 Определение токов и напряжений всех последовательностей в точке короткого замыкания. Построение векторных диаграмм

Полученные значения эквивалентные сопротивления прямой, обратной и нулевой последовательности позволяют вычислить коэффициент короткого замыкания К⁽ⁿ⁾ и шунт несимметричного короткого замыкания X_Δ⁽ⁿ⁾, которые позволят вычислить ток в поврежденных фазах. Коэффициент короткого замыкания с учетом заданного варианта равен: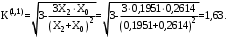

Шунт короткого замыкания равен: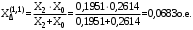

Вычислим токи в поврежденных фазах: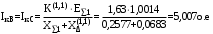

Схему замещения прямой последовательности можно заменить эквивалентной схемой, которая представлена на рисунке 13.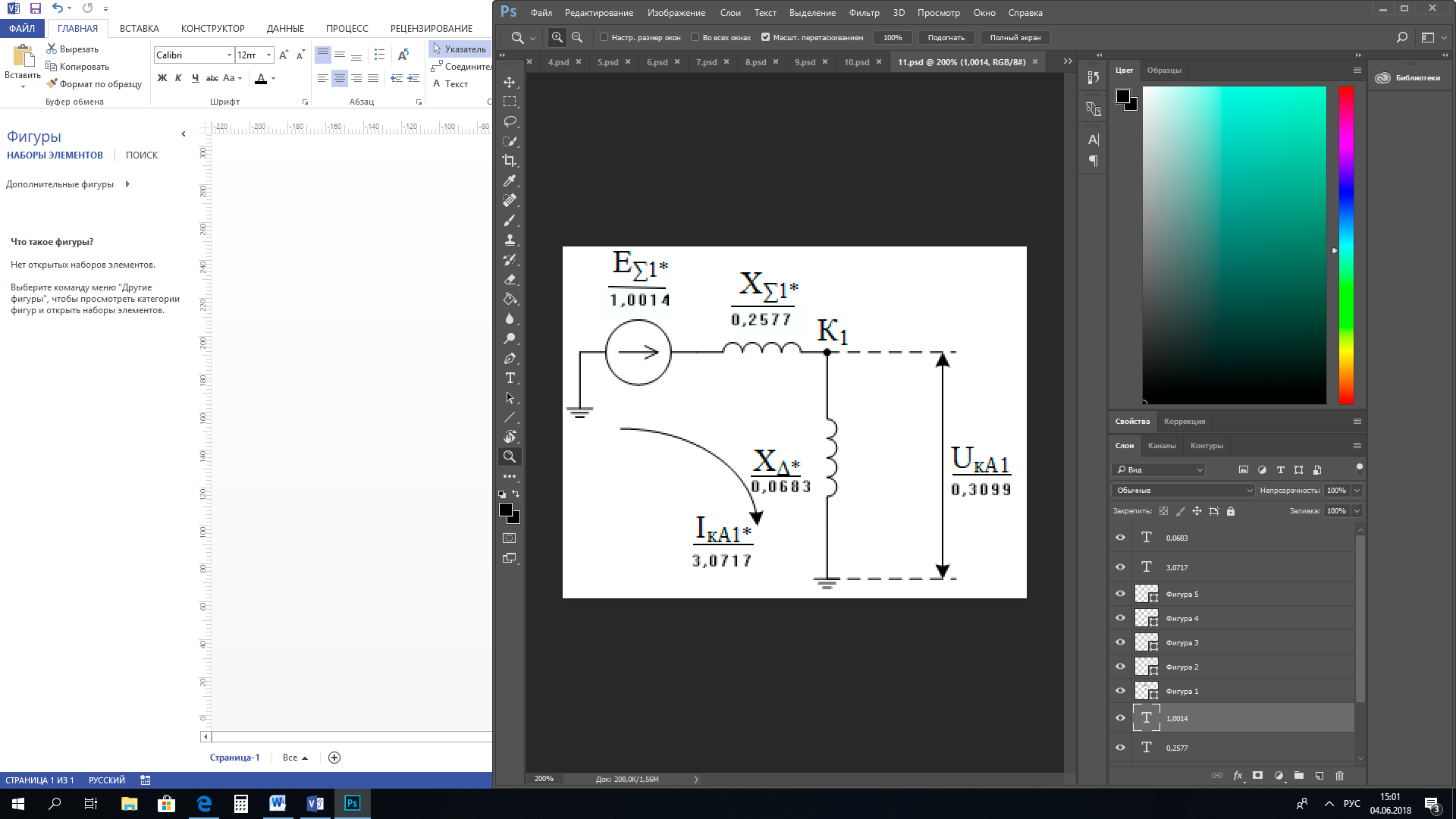

Рисунок 13 – Эквивалентная схема замещения прямой последовательности
На основании эквивалентной схемы можно вычислить ток в фазе А прямой последовательности: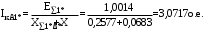

Зная ток, можно вычислить напряжение, которое падает на шунте: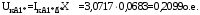

При этом стоит отметить, что это напряжение остается постоянным во всех последовательностях. Тогда вычислим ток в фазе А для оставшихся последовательностей: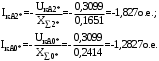

Проверим правильность найденных значений токов: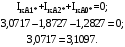

Погрешность составляет: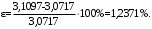

Погрешность составляет менее 5%, из этого следует, что расчет выполнен верно.

Для построения векторной диаграммы токов и напряжений осталось вычислить напряжения фаз В и С. Исходя из граничных условий заданного вида короткого замыкания, получим: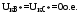

Векторные диаграммы токов и напряжения в месте короткого замыкания представлены на рисунке 14. По диаграммам определим модуль получившихся напряжений и токов, измерив длину векторов. После чего переведем из относительных единиц в именованные.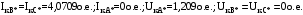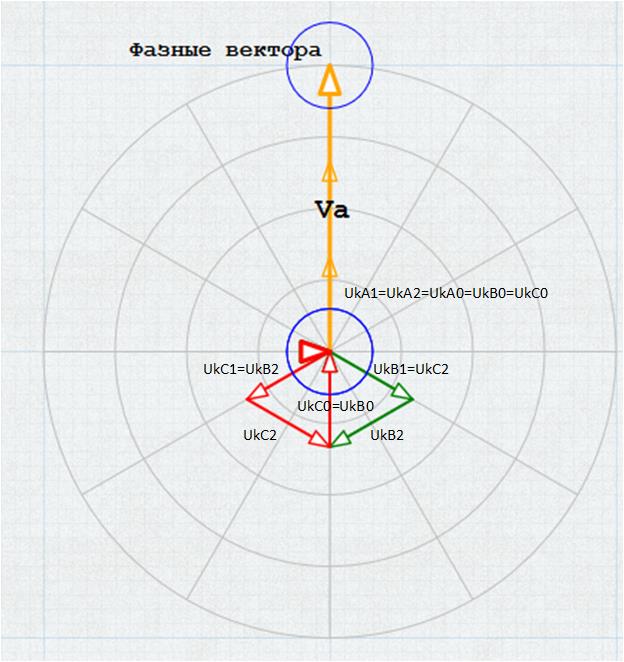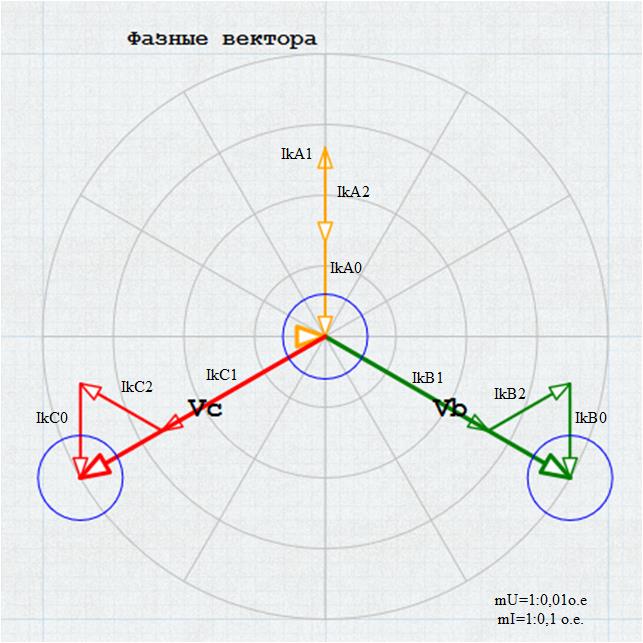

Рисунок 14 – Векторные диаграммы токов и напряжений в месте короткого замыкания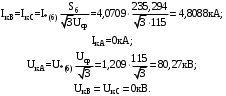

1.5 Определение токов и напряжений

Для нахождения параметров режима в заданном сечении необходимо поочередно произвести расчет в относительных единицах распределения тока в схеме каждой последовательности путем развертывания от схемы простейшего вида к исходной схеме, используя при этом законы теории линейных электрических цепей. Начальной точкой такого расчета является найденное значение напряжения в точке короткого замыкания соответствующей последовательности с учетом его знака и положительного направления.

Рисунок 15 – Первый этап развертывания простейшей схемы замещения прямой последовательности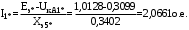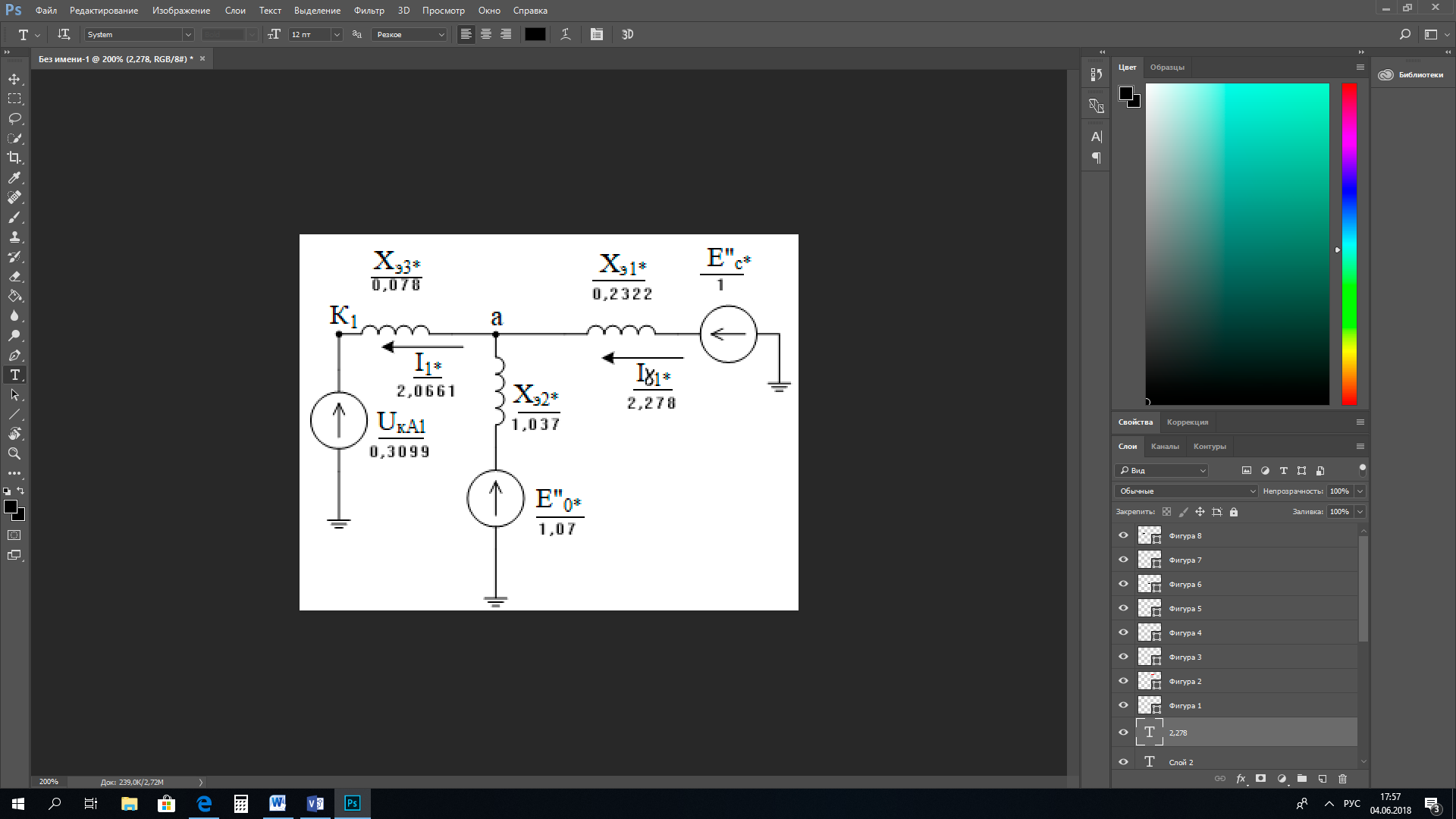

Рисунок16 – Второй этап развертывания простейшей схемы замещения прямой последовательности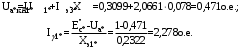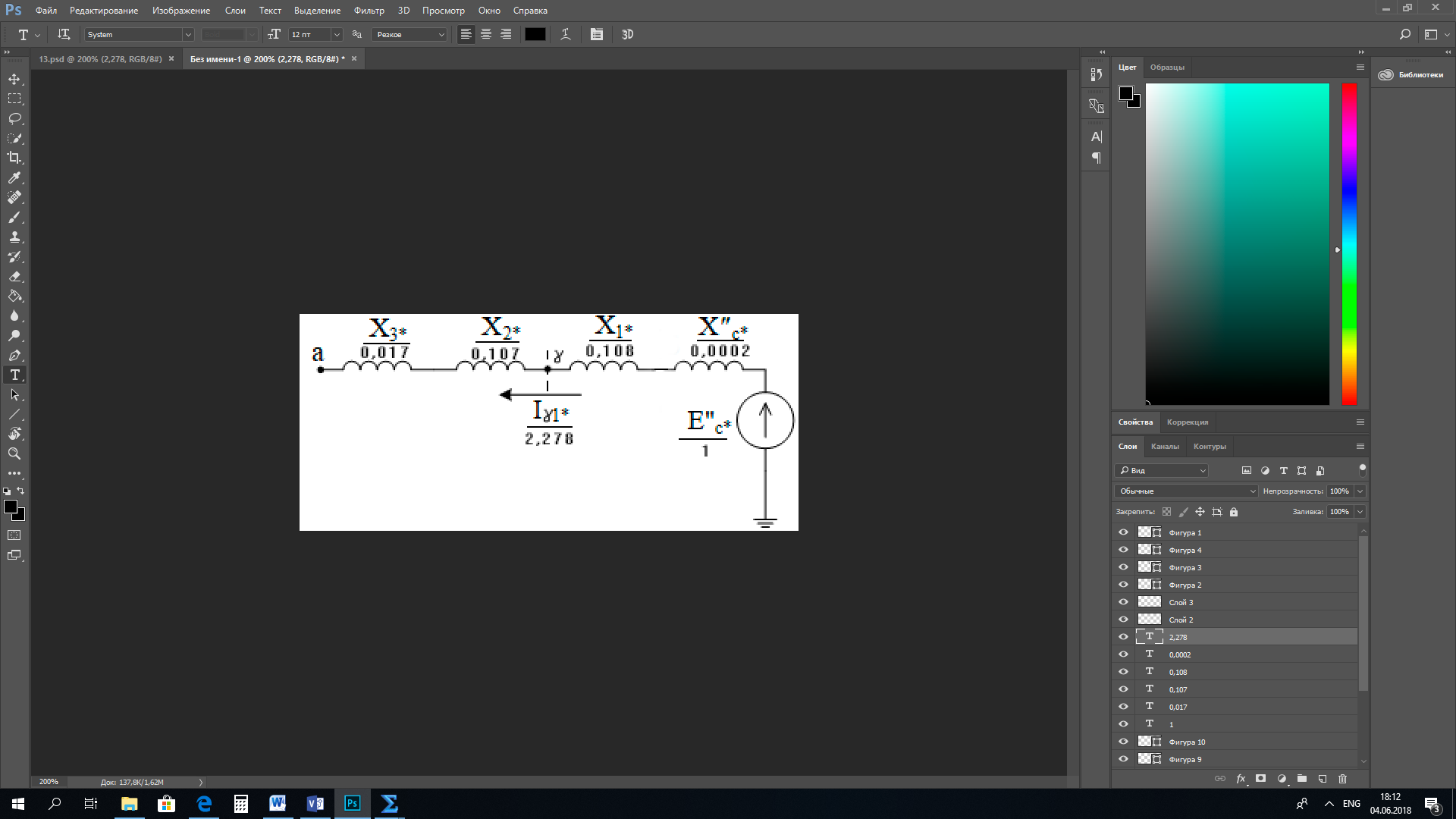

Рисунок 17 – Последний этап развертывания простейшей схемы замещения прямой последовательности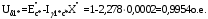

Теперь приступим к вычислению значения напряжения и тока в сечении для схемы замещения обратной последовательности.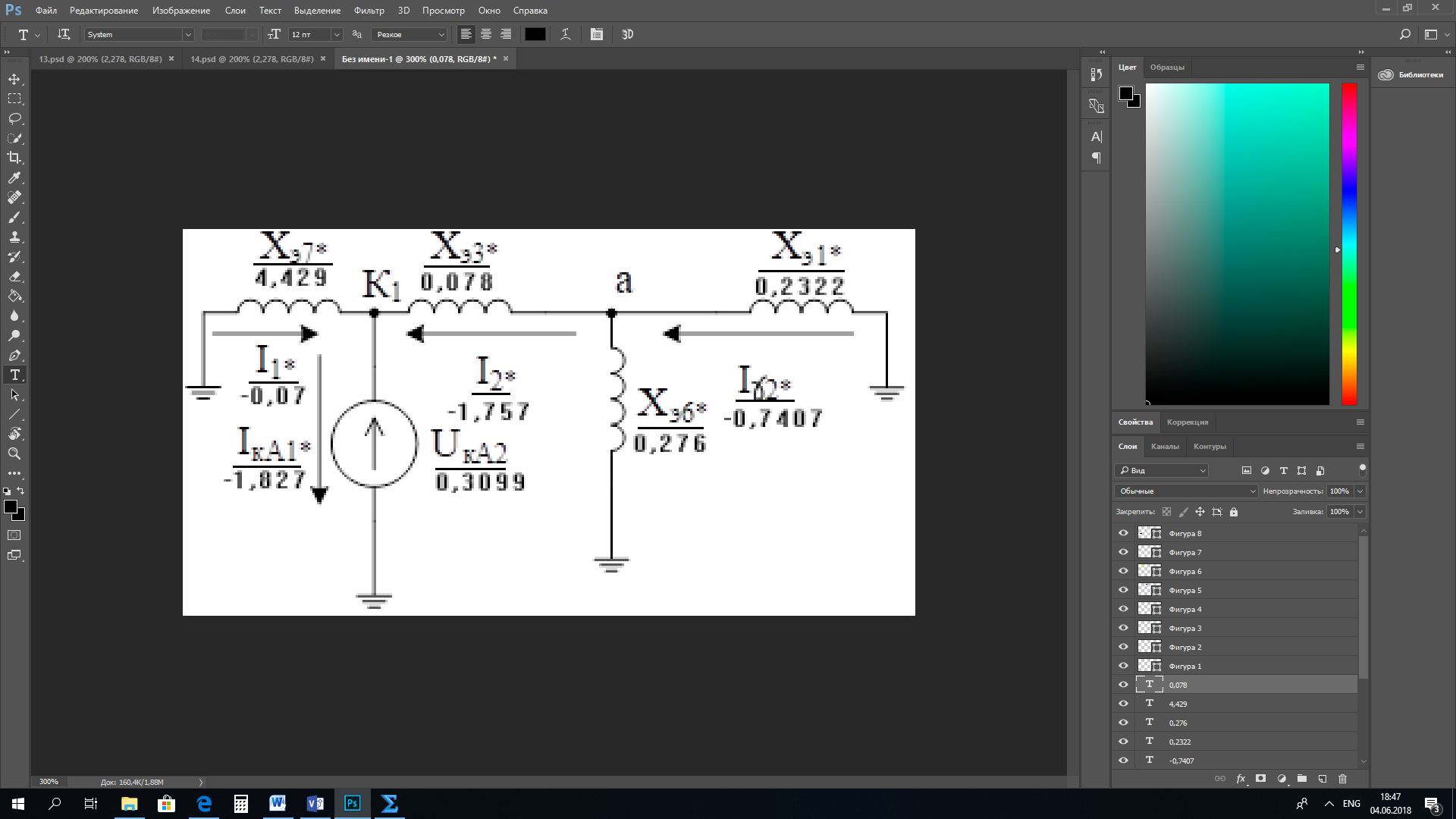

Рисунок 18 – Первый этап развертывания простейшей схемы замещения обратной последовательности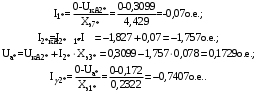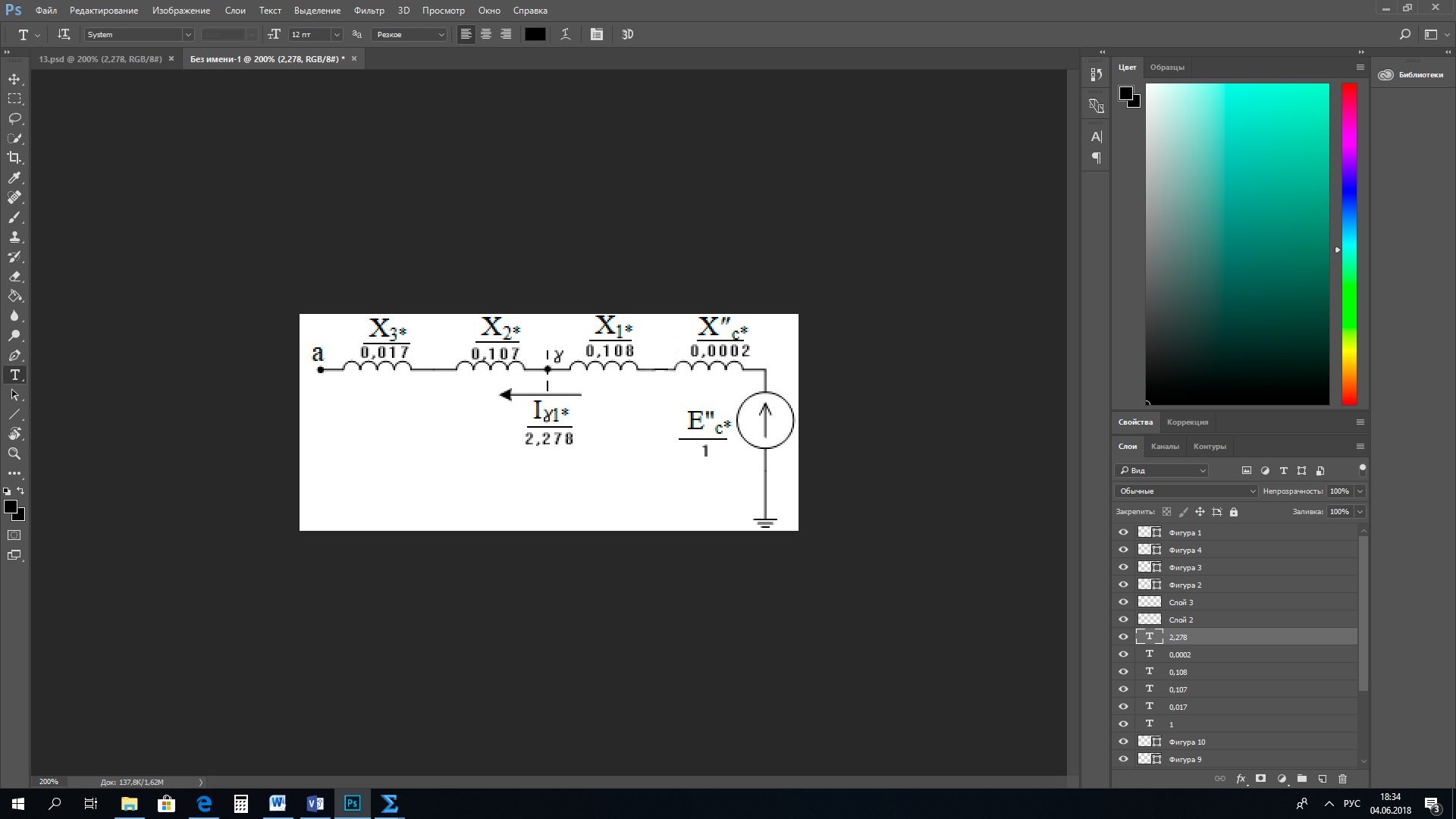

Рисунок 19 – Последний этап развертывания простейшей схемы замещения обратной последовательности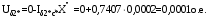

Приступим к определению значений напряжения и тока в сечении для схемы замещения нулевой последовательности.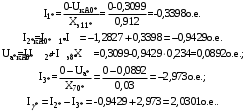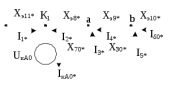

Рисунок 20 – Первый этап развертывания простейшей схемы замещения нулевой последовательности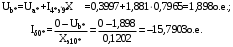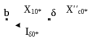

Рисунок 21 – Последний этап развертывания простейшей схемы замещения нулевой последовательности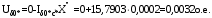

Построим векторные диаграммы токов и напряжений в сечении и представим их на рисунке 22 и 23. Поворота векторов напряжения и тока не произойдет, так как обмотки среднего и высшего напряжения в автотрансформаторах АТ – 1 и АТ – 2 являются одной единой первичной обмоткой, соответственно вектора в них будут сонаправлены.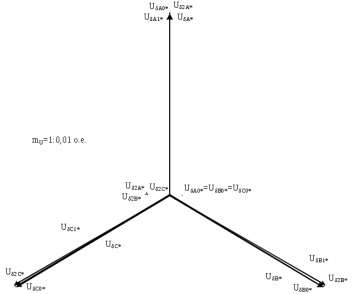

Рисунок 22 – Векторная диаграмма напряжений в сечении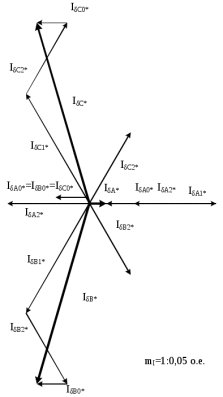

Рисунок 23 – Векторная диаграмма токов в сечении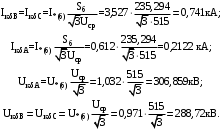

2 Расчет предела статической устойчивости станции системы электроснабжения предприятия

2.1 Составление схемы замещения. Расчет собственных и взаимных проводимостей схемы для узлов станции и системы

Схема замещения для расчета статической устойчивости выглядит также, как и схема замещения прямой последовательности, только отличие состоит в том, что нагрузка в ней представлена комплексным сопротивлением (без эдс), то есть: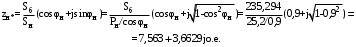

Помимо этого, генератор должен быть представлен своими переходными параметрами: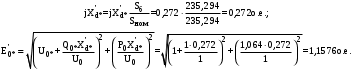

С учетом рассчитанных параметров представим на рисунке 24 схему замещения для расчета статической устойчивости.

Для вычисления собственных и взаимных проводимостей для узлов станции и системы удобнее всего применить метод единичных токов, суть которого заключается в том, что эдс системы заменяется на закороток, а ток в этой ветви приравнивается к единице. Далее вычисляются значения токов в оставшихся ветвях, а также величину эдс генератора. После чего находятся проводимости. Для осуществления данной операции потребуется преобразовать схему замещения для расчета статической устойчивости.

Рисунок 24 – Схема замещения для расчета статической устойчивости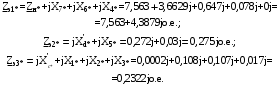

Тогда схема замещения примет вид, представленный на рисунке 25.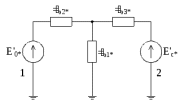

Рисунок 25 – Упрощенная схема замещения для расчета статической устойчивости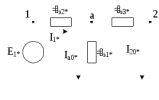

Рисунок 26 – Схема для расчета методом единичного тока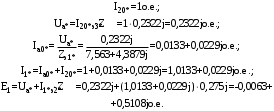

Вычислим собственные и взаимные проводимости для узлов станции и генератора: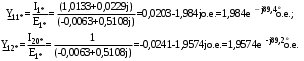

Дополнительные углы: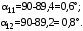

2.2 Построение угловой характеристики

Уточним значение эдс системы: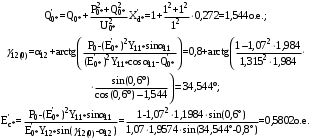

Запишем уравнение угловой характеристики: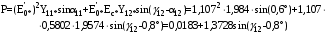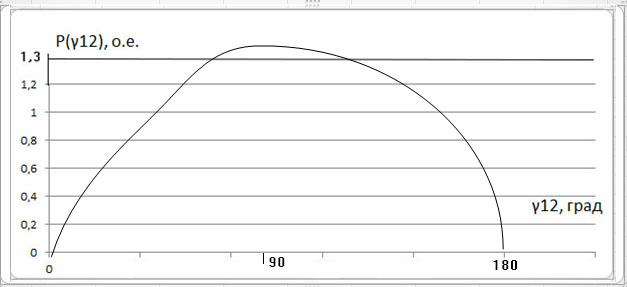

Рисунок 27 – Угловая характеристика

2.3 Расчет запаса статической устойчивости

Коэффициент запаса статической устойчивости находится по следующей формуле: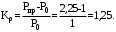

Нормативный коэффициент запаса статической устойчивости в нормальном режиме работе должен быть не менее 0,2. Из этого следует, что система для заданного варианта статически устойчива.

3 Расчет динамической устойчивости системы

3.1 Построение угловых характеристик для нормального, аварийного и послеаварийного режимов

Для нормального режима угловую характеристику возьмем из пункта 2.2. Для аварийного режима схема замещения выглядит также, как и для анализа статического устойчивости, только в точке короткого замыкания включается аварийный шунт jX_Δ^(1,1). Представим ее на рисунке 28.

Рисунок 28 – Схема замещения для аварийного режима
Упростим схему используя следующие выражения: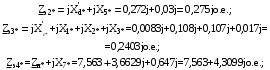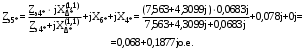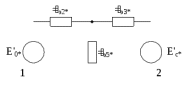

Рисунок 29 – Упрощенная схема замещения аварийного режима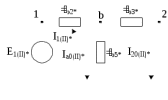

Рисунок 30 – Схема для расчета аварийного режима методом единичного тока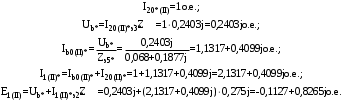

Определим собственные и взаимные проводимости для узлов станции и системы в аварийном режиме: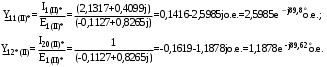

Дополнительные углы: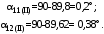

Уточним значение ЭДС системы для аварийного режима: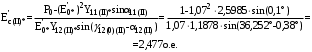

Запишем уравнение угловой характеристики: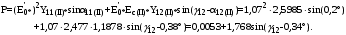

Таблица 4 – Координаты построения угловой характеристики для аварийного режима

δ₁₂, º	0		10	20		30		40		50		60		70		80		90
P(δ₁₂), о.е.	0,011		0,453	1,001		1,397		1,871		2,1		2,438		2,736		2,88		2,904
δ₁₂, º	100	110			120		130		140		150		160		170		180
P(δ₁₂), о.е.	2,88	2,736			2,438		2,1		1,871		1,397		1,001		0,453		-0,001

Теперь построим угловую характеристику для послеаварийного режима, то есть, когда аварийный участок линии отключится и включится смежная линия. Представим схему замещения на рисунке 31.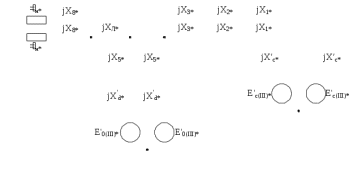

Рисунок 31 – Схема замещения для расчета послеаварийного режима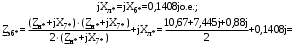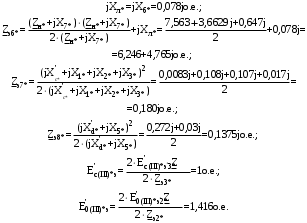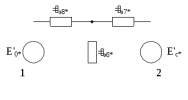

Рисунок 32 – Упрощенная схема замещения для расчета послеаварийного режима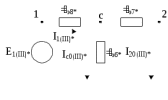

Рисунок 33 – Схема для расчета послеаварийного режима методом единичного тока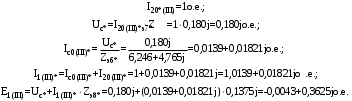

Вычислим собственные и взаимные проводимости для узлов станции и системы в послеаварийном режиме: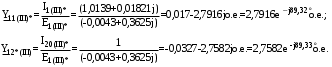

Дополнительные углы: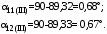

Уточним значение ЭДС системы для аварийного режима: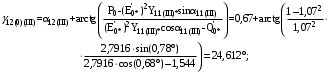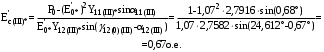

Запишем уравнение угловой характеристики: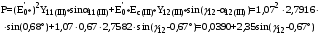

Таблица 5 – Координаты построения угловой характеристики для послеаварийного режима

δ₁₂, º	0	10		20		30		40		50		60		70		80		90
P(δ₁₂), о.е.	0,166	1,11		2,107		3,128		3,905		4,517		5,22		5,519		5,707		5,882
δ₁₂, º	100		110		120		130		140		150		160		170		180
P(δ₁₂), о.е.	5,674		5,423		4,878		4,221		3,597		2,44		1,626		0,843		-0,11

3.2 Определение предельного угла отключения

Предельный угол отключения определяется на семействе угловых характеристик трех режимов: нормального (I), аварийного (II) и послеаварийного (III). Отключать линию требуется в том случае, если площадка торможения будет меньше, чем площадка ускорения, то есть генератор в таком случае выпадет из синхронизма. Соответственно, отключая линию, рабочая точка генератора переходит на новую характеристику, тем самым увеличивая площадку торможения. В нашем случае площадки торможения предостаточно и отключения не требуется, соответственно, предельного угла отключения не существует. На рисунке 34 представлено семейство угловых характеристик для трех режимов, а также графически равные площадки ускорения и торможения, откуда легко определить угол максимального отклонения ротора генератора δ₁₂, который равен 36,815º. Из всего этого следует, что система динамически устойчива.

Рисунок 34 – Семейство угловых характеристик и определение угла максимального отклонения ротора генератора

3.3 Решение уравнение движения ротора генератора

Дифференциальное уравнение движения ротора генератора в режиме короткого замыкания имеет следующий вид: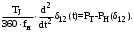

Удобнее всего решить данное дифференциальное уравнение методом последовательных интервалов, суть которого заключается в разбиении временного интервала на участки и расчет приращения функции на каждом участке. Постоянную инерции агрегата T_J приведем к базисной мощности: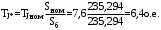

Разобьем временную ось на интервалы с шагом Δt = 0,05 с, причем максимальное значение времени выберем заданное время отключения. Определим приращение угла Δδ на первом интервале (t = 0,05 c):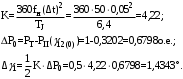

Тогда значение угла в конце первого интервала: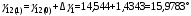

Продолжим вычисления. Приращение угла на втором интервале (t = 0,1 c):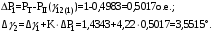

Угол в конце второго интервала: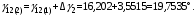

Аналогичным образом посчитаем для всех интервалов и результаты расчетов сведем в таблицу.
Таблица 6 – Результаты расчетов методом последовательных интервалов

t, с	0	0,05	0,1	0,15	0,2	0,25	0,3	0,35
δ₁₂, º	9	10,622	15,006	24,31	31,971	35,801	37,144	34,99

На рисунке 35 построим график зависимости угла δ₁₂ от времени t. Также нанесем на график прямую, показывающую найденные из рисунка 34 угол максимального отклонения ротора генератора, и прямую, показывающую заданное время отключения. Из графика видно, что угол отклонения ротора генератора при решении дифференциального уравнения движения не превышает угол, который был найден по методу площадей, а значит, предельного времени отключения не существует, то есть отключение не требуется. Из этого следует подтверждение ранее сделанному выводу: система динамически устойчива и отключение поврежденной линии не требуется.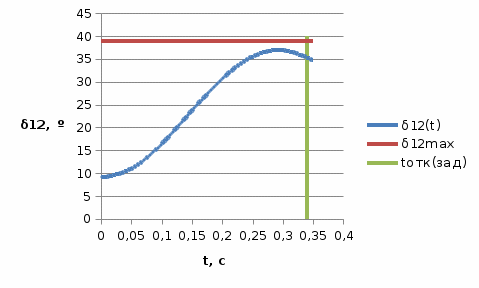

Рисунок 35 – График зависимости f = δ₁₂(t)

Заключение

В данном курсовом проекте был произведен расчет токов короткого замыкания, а именно, ток трехфазного короткого замыкания и ток двухфазного короткого замыкания на землю.

Как показали расчёты, эта система статически устойчива, об этом говорит коэффициент запаса статической устойчивости. Ещё была графически построена угловая характеристика активной мощности генератора для нормального режима работы.

В результате расчета динамической устойчивости системы были построены угловые характеристики активной мощности генератора для аварийного и послеаварийного режимов, угловые характеристики всех трех режимов совмещены на одном рисунке. В заключение был построен график изменения угла положения ротора генератора во времени.

Список литературы

1. Зацепин, Е.П. Расчет переходных режимов и анализ устойчивости системы электроснабжения крупного промышленного предприятия [Текст]: Уч. пособие / Е.П. Зацепин, В.И. Зацепина, – Липецк: ЛГТУ, 2015. – 75 с.

2. Бессонов, Л. А. Теоретические основы электротехники [Текст]/ Л. А. Бессонов. – М. : Высш. шк., 1973. – 752 c.

3. СТО-13-2016 Студенческие работы. Общие требования к оформлению. Липецк : ЛГТУ, 2016, 32 с.