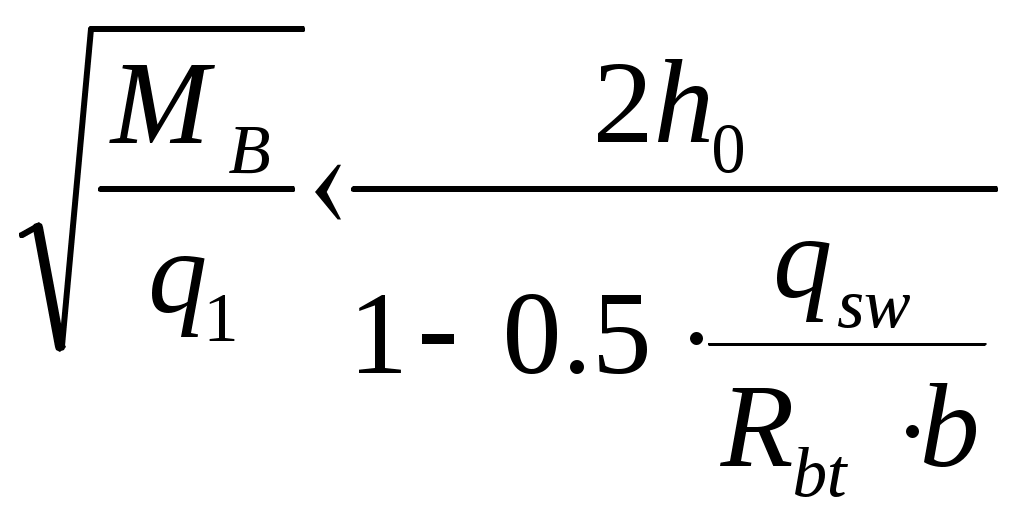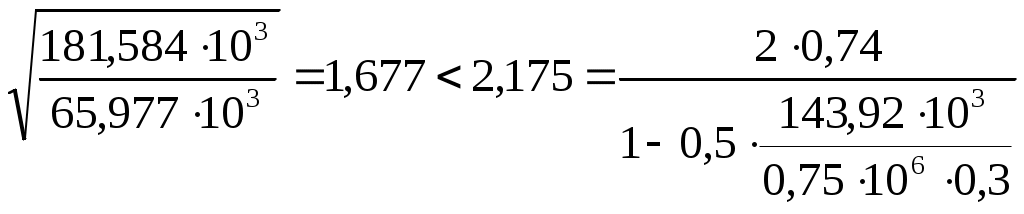курсовой жбк. Курсовой проект 1 ЖБК. Курсовой проект по учебному курсу Железобетонные и каменные конструкции 2 Студент (И. О. Фамилия)

• Название: Курсовой проект по учебному курсу Железобетонные и каменные конструкции 2 Студент (И. О. Фамилия)
• Анкор: курсовой жбк
• Дата: 25.03.2022
• Размер: 3.04 Mb.
• Имя файла: Курсовой проект 1 ЖБК.doc
• Тип: Курсовой проект; #415075
• страница: 4 из 6

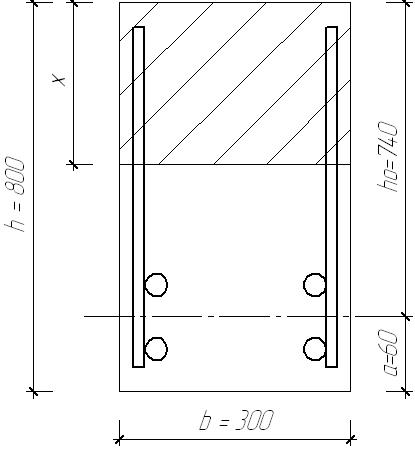
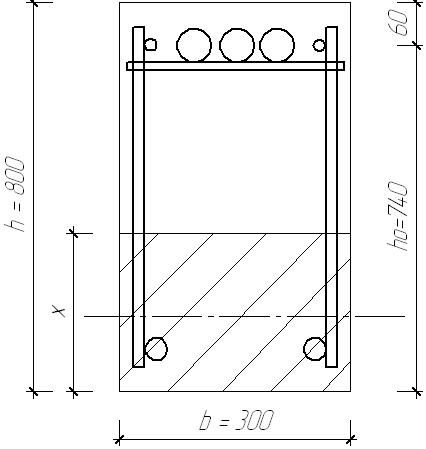
2.1.3. Расчетное сечение плиты.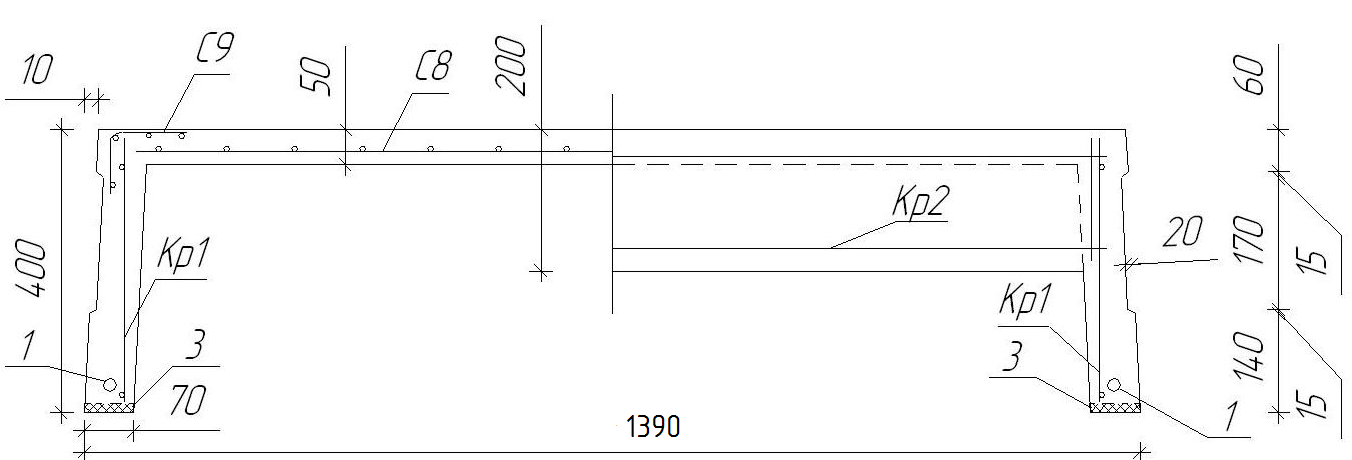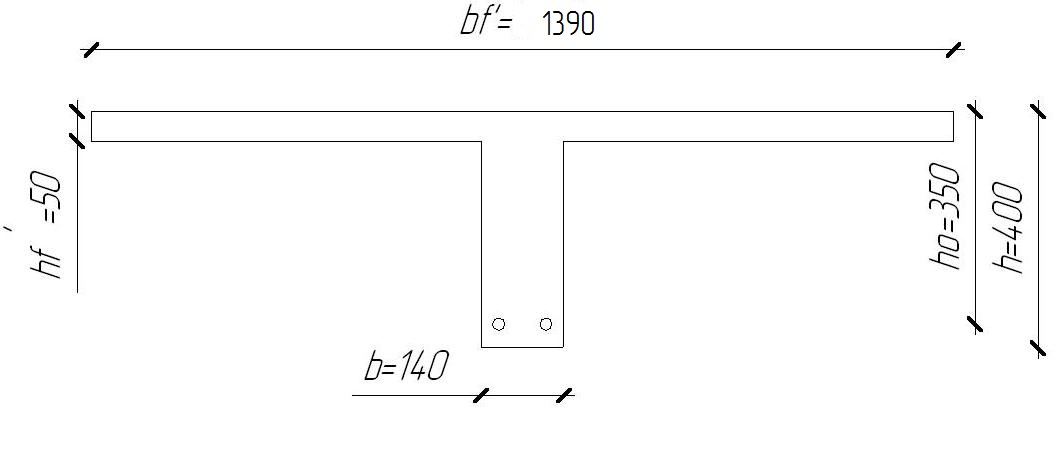

h=400мм

2.1.4. Характеристики прочности бетона и арматуры.

Монолитную предварительно напряженную плиту армируют стержневой арматурой класса А-600 с термическим натяжением.
Бетон тяжелый класса В20, соответствующий напря­гаемой арматуре .

- Призменная прочность бетона нормативная:

МПа;

- Расчетная:

;

- Расчетное сопротивление при растя­жении:

;

Начальный модуль упругости бетона Е_b=27500 МПа.
Арматура продольных ребер - класса А-600.

- Норма­тивное сопротивление:

;

- Расчетное:

;

Модуль упругости E_s=190 000 МПа.

Предварительное напряжение арматуры принимают равным σ_sp=0,6х815=489МПа.

2.1.5. Расчет прочности плиты по нормальному сечению.

Определим положение нейтральной оси:









<sub>Вывод: условие выполняется, следовательно нейтральная ось находится в полке.
Определяем площадь растянутой арматуры: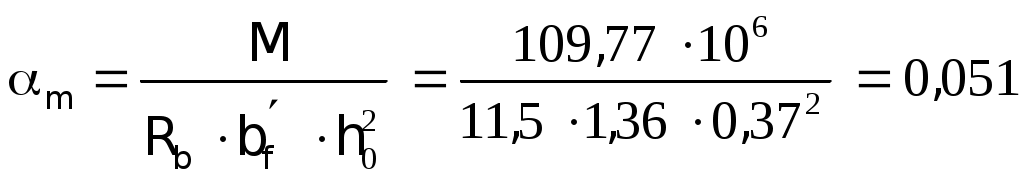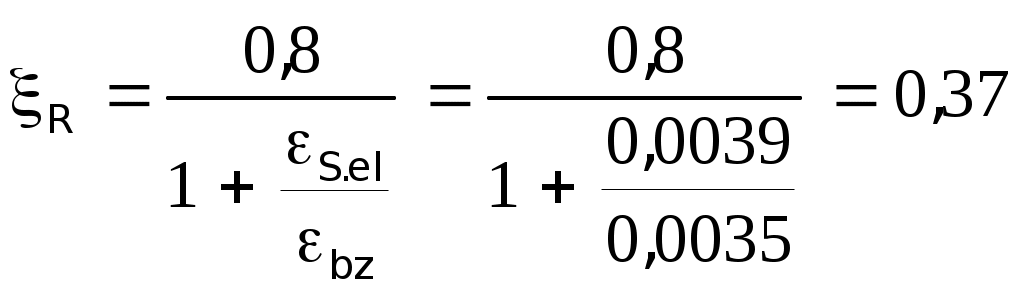









арматура в сжатой зоне не требуется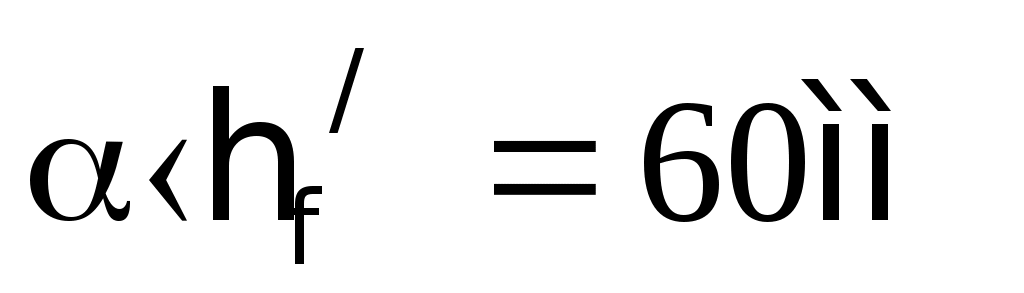





граница сжатой зоны проходит в полке



>1,1 принимаем</sub>
Принимаем арматуру 216мм, A_s = 402 мм²

2.1.6. Определение геометрических характеристик приве­денного сечения.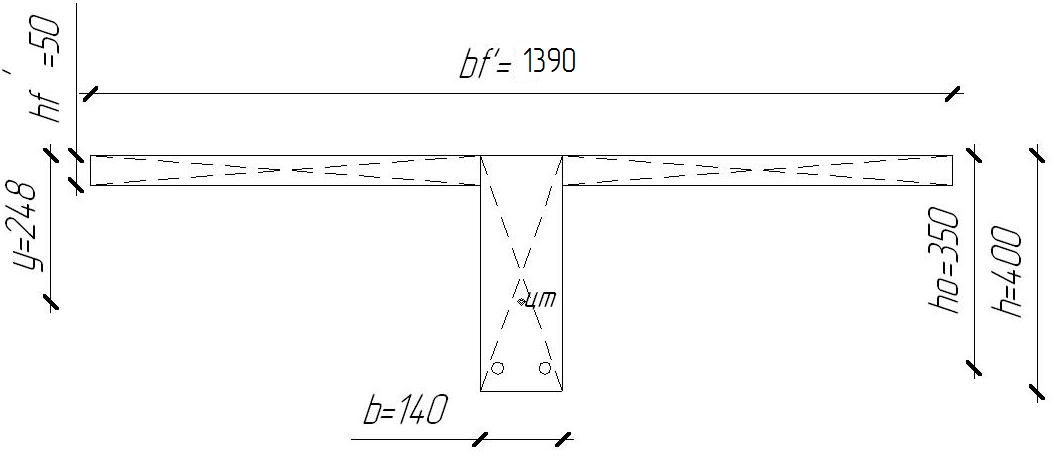

Отношение мо­дулей упругости:



Пло­щадь приведенного сечения:



Статический момент площади приведенного сечения относительно нижней грани: .

Расстояние от нижней грани до центра тяжести приведенного сечения:



Момент инерции приведенного сечения: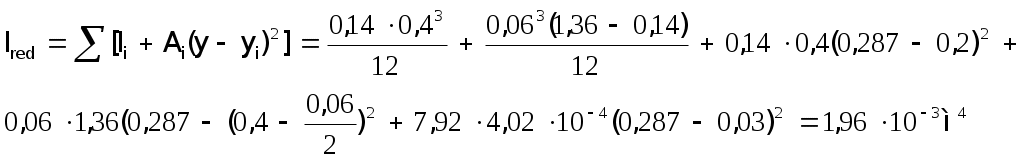

2.1.7. Определение потерь предварительного напряжения арматуры.

Определяем 1ые потери:

- Потери от релаксации напряжений в арма­туре при электротермическом способе натяжения:

.

- Потери от температурного перепада между натянутой арматурой и упорами: .

- Потери от деформации форм:



- Потери от деформации анкеров:

.

Усилия обжатия с учетом 1-х потерь:



Эксцентриситет этого усилия относительно центра тяжести сечения:

.

Напряжение в бетоне при обжатии:


Определяем 2ые потери:

- Потери от усадки:



- Потери от ползучести: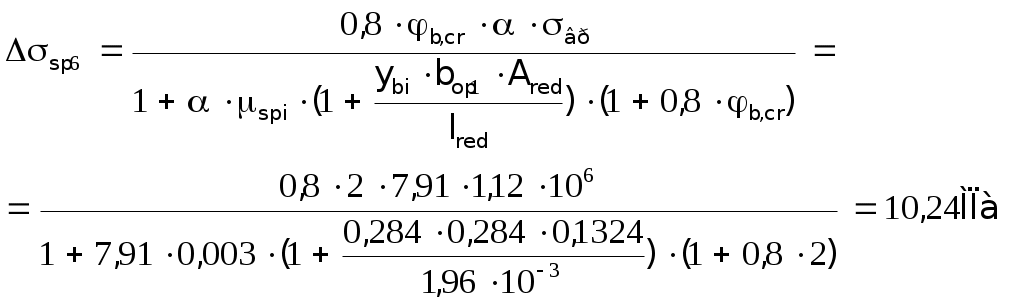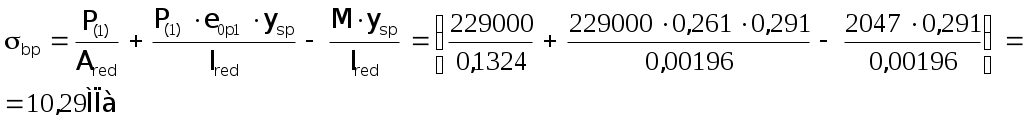







Сумма вторых потерь:



Сумма 1-х и 2-х потерь:

_{<100 поэтому значение суммы 1-х и 2-х потерь принимаем равным100 МПа}

Полные потери:

.

Усилия предварительного обжатия бетона с учетом всех потерь:

2.1.8. Расчет прочности плиты по наклонному сечению.

Проверим условие:







71,4кН <193,2кН

Условие выполняется.
Расчёт плиты на действие поперечной силы по наклонному сечению:



где -поперечная сила в наклонном сечении с длиной проекции С

-поперечная сила воспринимаемая бетоном в наклонном сечении

-поперечная сила воспринимаемая поперечной арматурой в наклонном сечении.

Поперечная арматура класса А300.

Из условия свариваемости устанавливается минимальный диаметр поперечных стержней-6мм,

В приопорной зоне (1/4 пролёта) арматура устанавливается с шагом и => s_w=150мм.

В середине пролёта на расстоянии ½ l и s_w=250мм.

Определим интенсивность хомутов: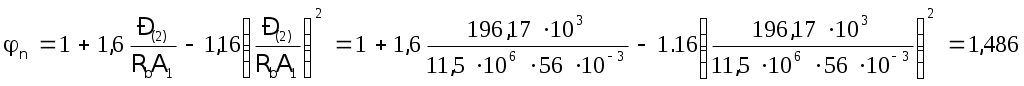









Хомуты учитываются в расчёте, если соблюдается условие:






Если нагрузка включает временную, то расчётное значение равномерно распределённой нагрузки:



Определяем значение С: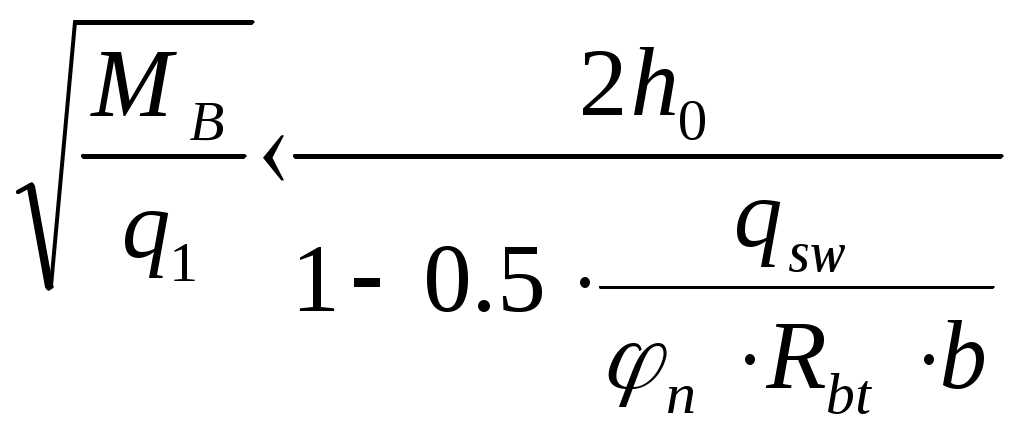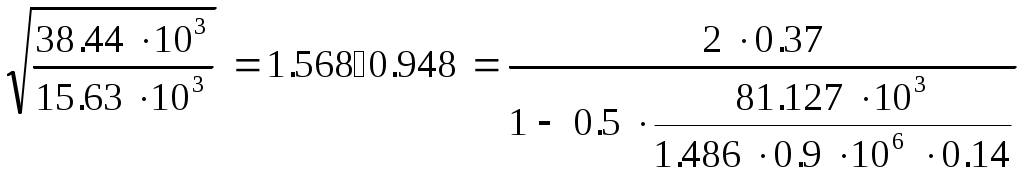





=>



принимаем с=1,11м

















Условие выполняется.

2.1.9. Расчет по образованию трещин, нормальных к продольной оси.

Выполняют для необходимости проверки по раскрытию трещин. Для элементов, к трещиностойкости которых предъявлены требования третьей категории, приняты значения коэффициентов надежности по нагрузке . .

Условие: .

Для предварительно напряженных элементов в стадии эксплуатации:

,






.

Т.к. условие не выполняется, то образуются трещины в растянутой зоне.

Определение ширины раскрытия трещин.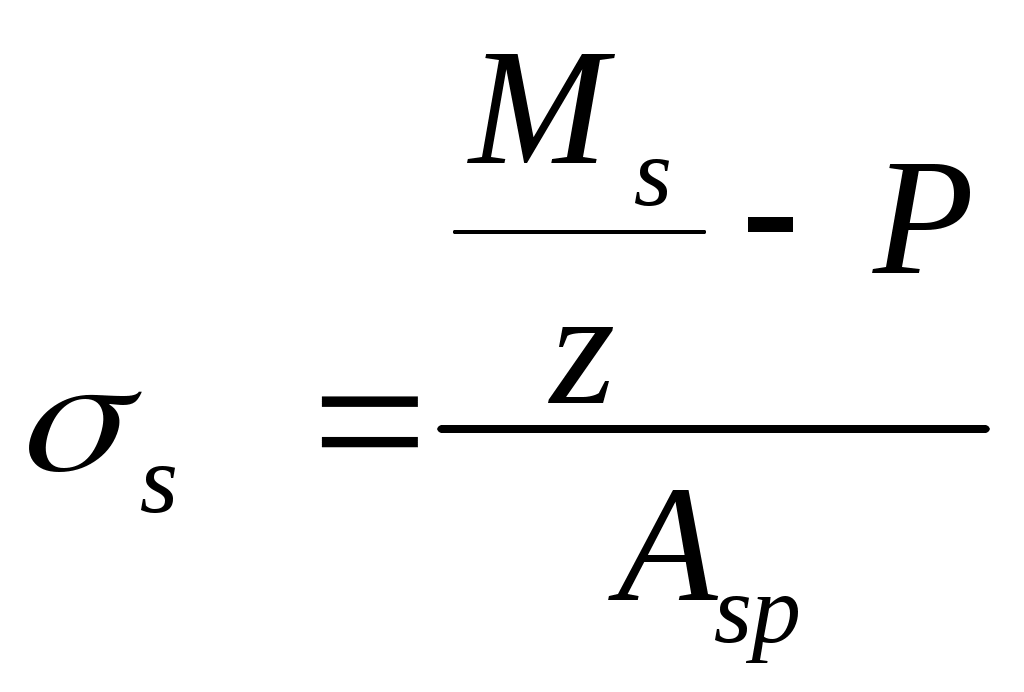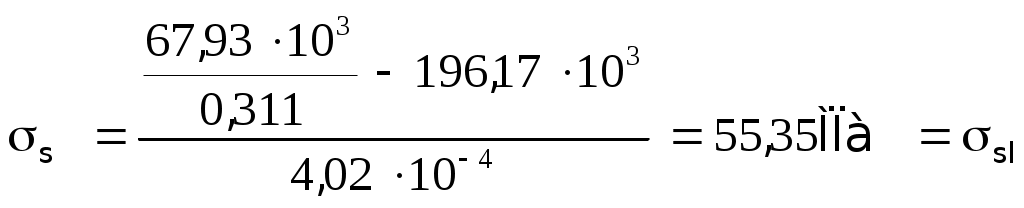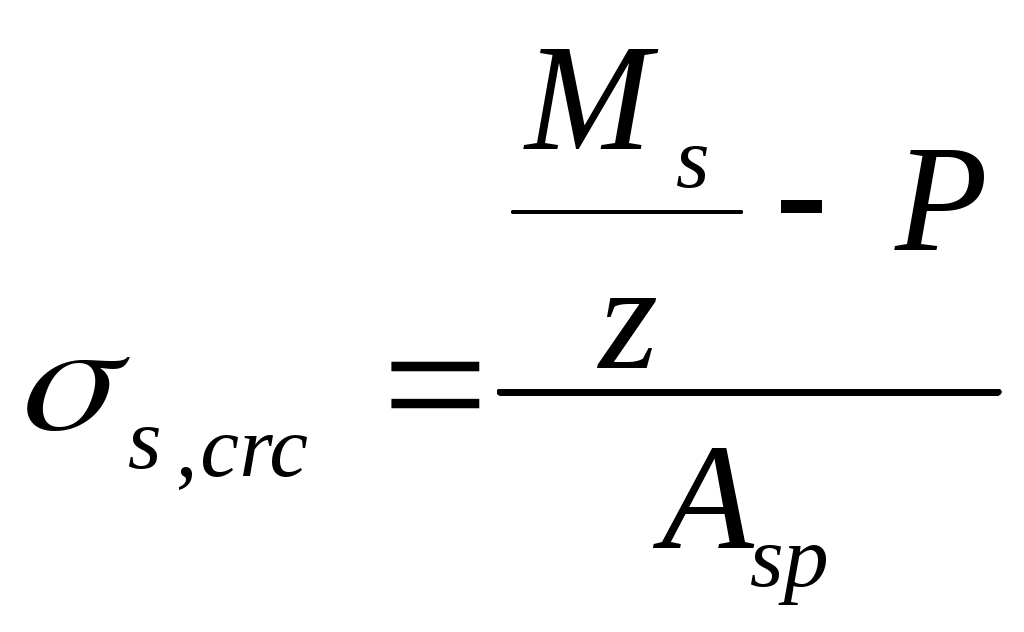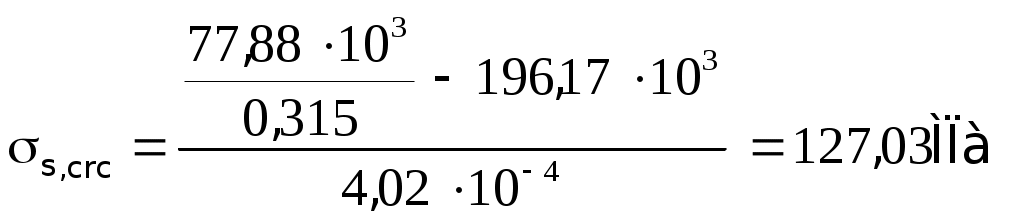



<sub>при непродолжительном раскрытии трещин

при продолжительном раскрытии трещин














































Т.к. σs,crc> σs, то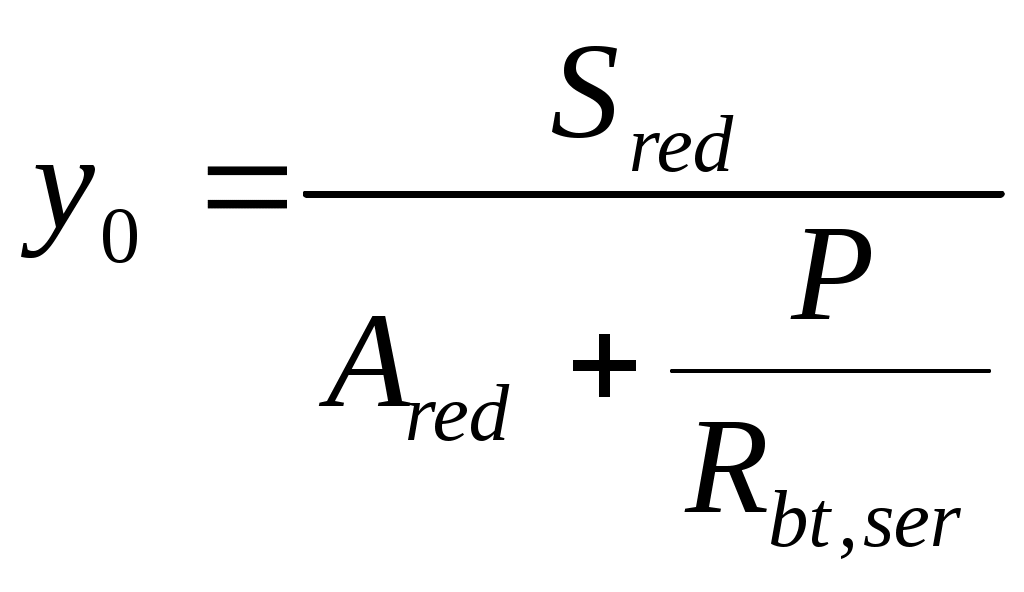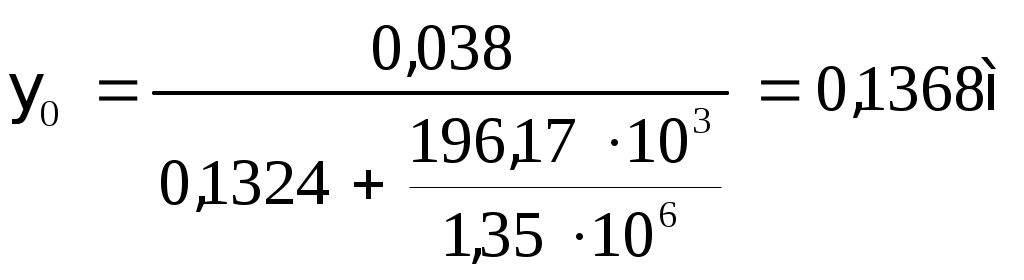













k=0,9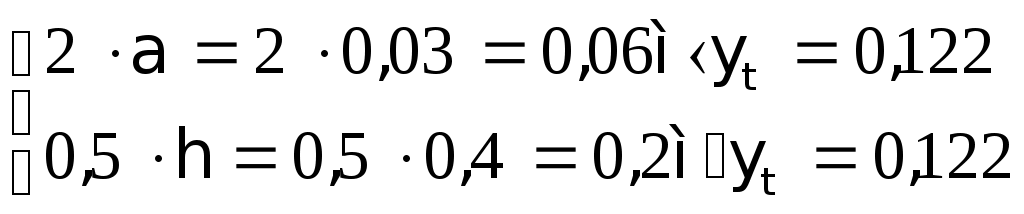









ds=0,018м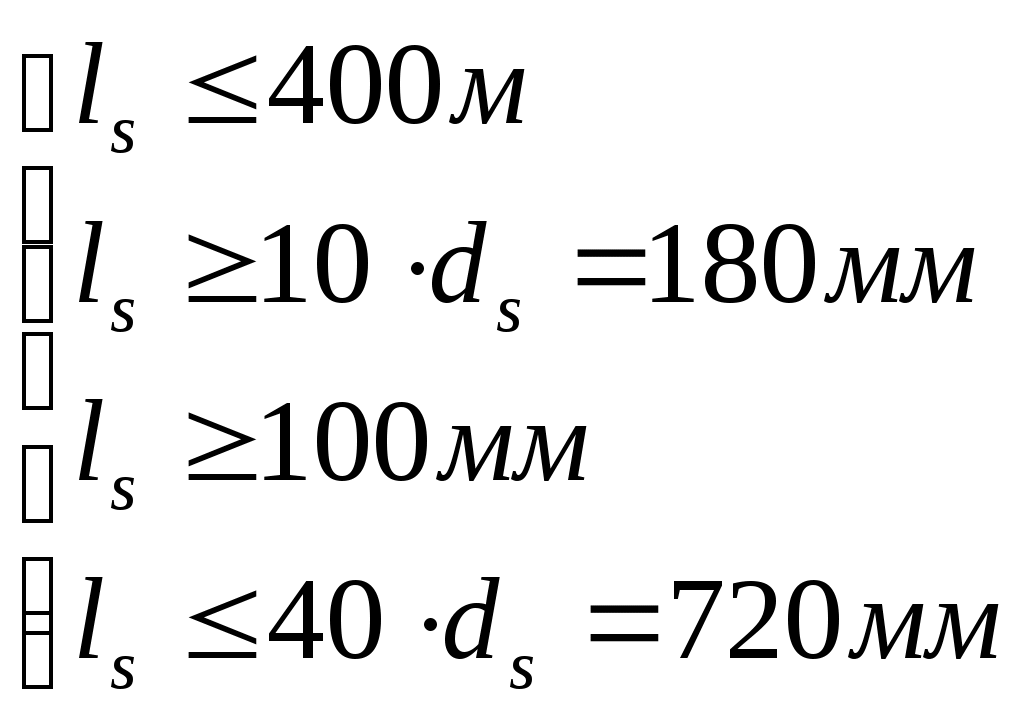

ls=380мм







σsопределяется от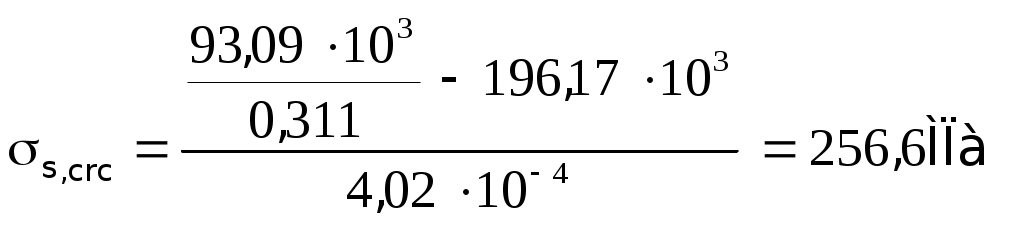













Предельная допускаемая ширина раскрытия трещин при продолжительном и непродолжительном раскрытии 0,2 мм и 0,3 мм соответственно.

t=0,59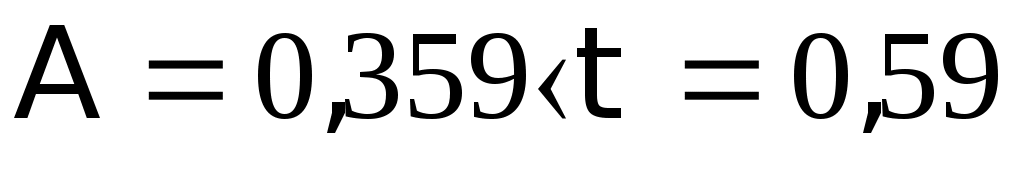

,

следовательно</sub>

2.1.10. Расчет прогиба плиты.

Величина прогиба при работе элемента с трещинами вычисляется:









_40%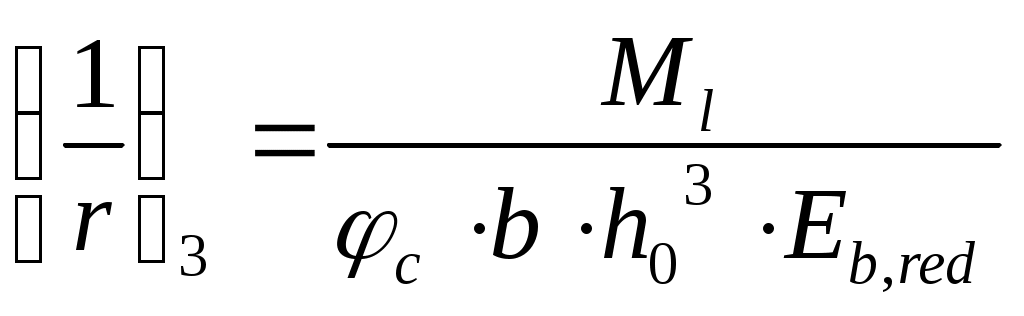


























2.2. Расчет ригеля.

2.2.1. Расчетная схема и нагрузки.

Поперечная многоэтажная рама имеет регулярную расчетную схему с равными пролетами ригелей и равными длинами стоек (высотами этажей). Сечения ригелей и стоек по этажам приняты постоянными. Многоэтажную раму расчленяют для расчета на вертикальную нагрузку на одноэтажные рамы с нулевыми точками моментов – шарнирами, расположенными по концам стоек.

Нагрузка на ригель от ребристых плит считается равномерно распределенной. Ширина грузовой полосы на ригель равна шагу поперечных рам 6,3м.

Вычисляется расчетная нагрузка на 1погонный м ригеля.

- Постоянная:

от перекрытия с учетом коэффициента надежности по назначению здания :

от веса ригеля с учетом коэффициентов надежности и :



- Временная: с учетом ;



- Полная нагрузка:

.

2.2.2. Вычисление изгибающих моментов в расчетных сечениях.

Рассчитываем ригель прямоугольного сечения размерами 300х800 мм.

м⁴

м⁴



_{1-е загружение:}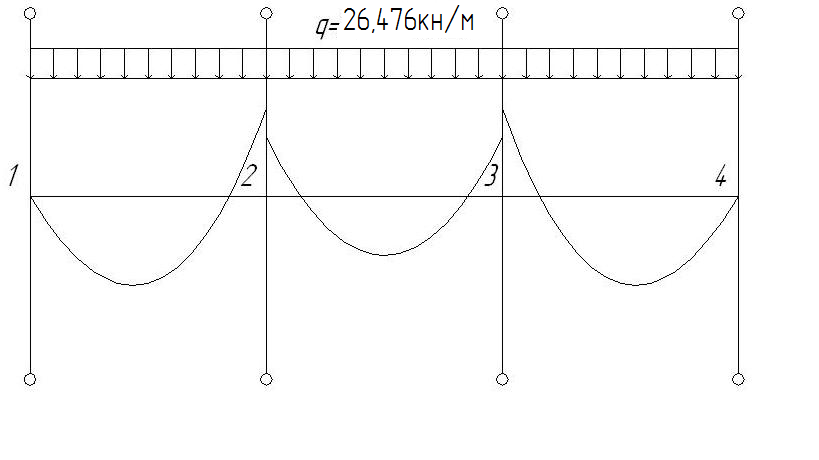



По приложению 11 подбираем α и вычисляем опорные моменты:









_{2-е загружение:}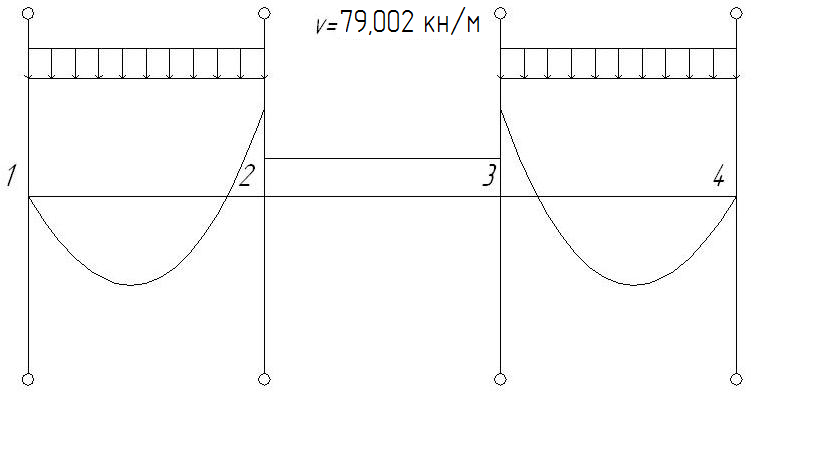


По приложению 11 подбираем β и вычисляем опорные моменты:









_{3-е загружение:}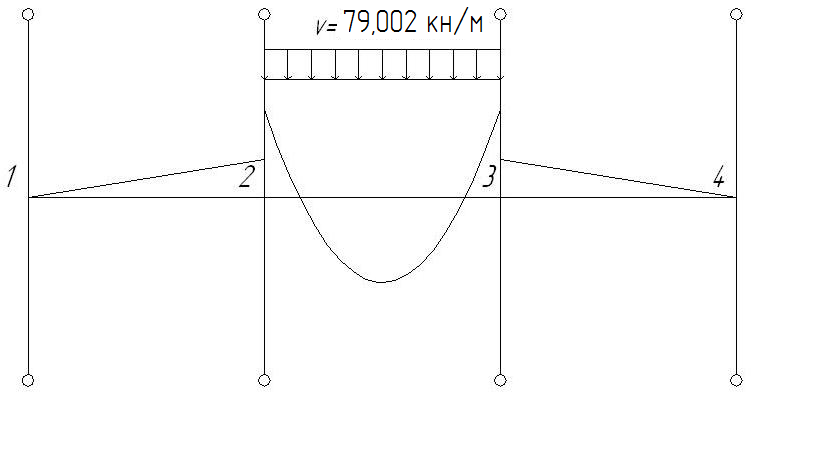


По приложению 11 подбираем β и вычисляем опорные моменты:









_{4ое загружение:}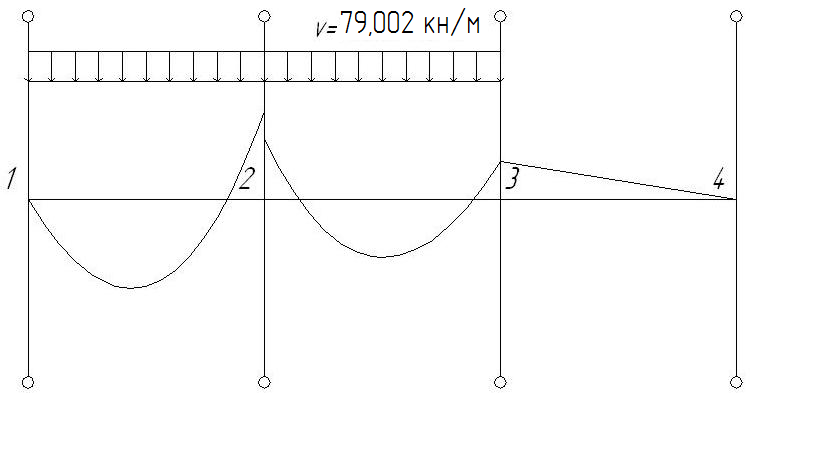

По приложению 11 подбираем β и вычисляем опорные моменты:











2.2.3. Определение перерезывающих сил и максимальных пролетных моментов.
Загружение 1+2:
- Пролет 1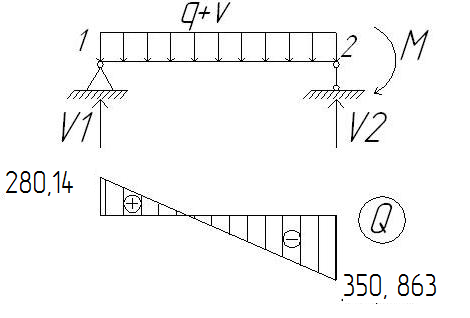















- Пролет 2



Загружение 1+3:
- Пролет 1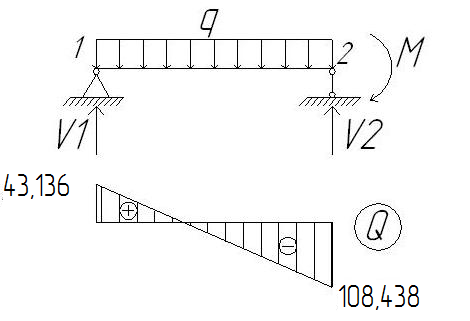


















- Пролет 2





Загружение 1+4:

- Пролет 1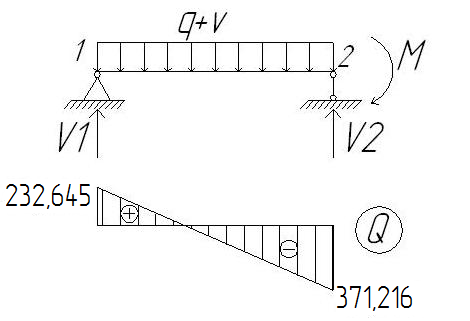















- Пролет 2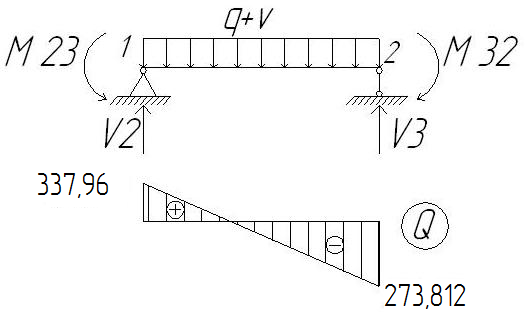


















_{Построим эпюры от сочетания загружений 1+2, 1+3, 1+4:}

Nпп	Схема загружения	Опорные моменты, кНм				Мmax, кНм		Привязка х, м
		M12	M21	M23	M32	1 пролет	Средний пролет	1 пролет	Средний пролет
1	1	0	93,71	85,5	85,5	-	-	-	-
2	2	0	186,43	95,674	95,674	-	-	-	-
3	3	0	93,216	159,45	159,45	-	-	-	-
4	4	0	302,95	297,65	111,62	-	-	-	-
5	1+2	0	280,14	181,174	181,174	302,663	15,567	2,398	Мmax в середине пролета
6	1+3	0	186,916	244,95	244,95	105,39	113,618	1,692
7	1+4	0	396,66	383,15	197,12	256,563	158,275	2,205	3,204

Произведем перераспределение моментов. Его суть состоит в том, что мы на опорах допускаем образование пластических шарниров, уменьшая тем самым расчетный опорный момент.

К эпюре схем загружения 1+4 добавлим выравнивающую эпюру моментов так, чтобы уравнялись опорные моменты и были обеспечены удобства армирования опорного узла.











Загружение 1+4:
- Пролет 1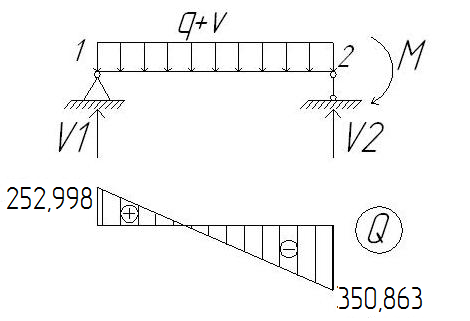















- Пролет 2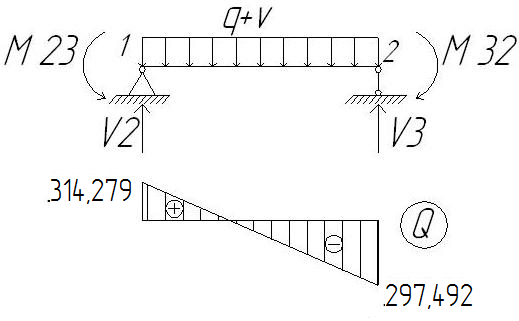

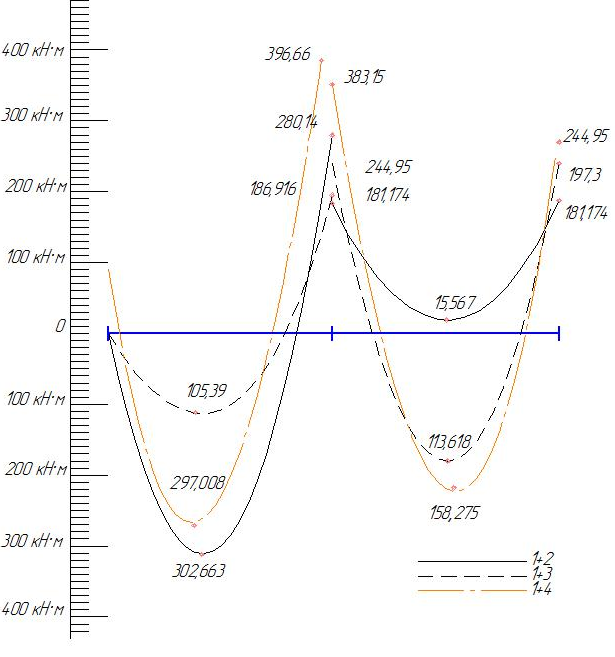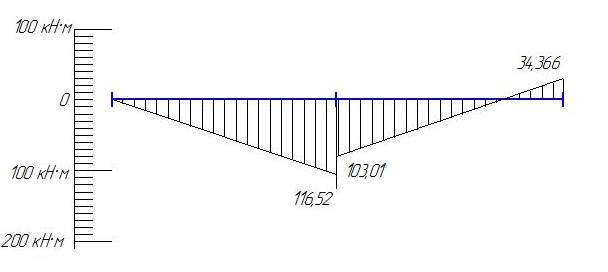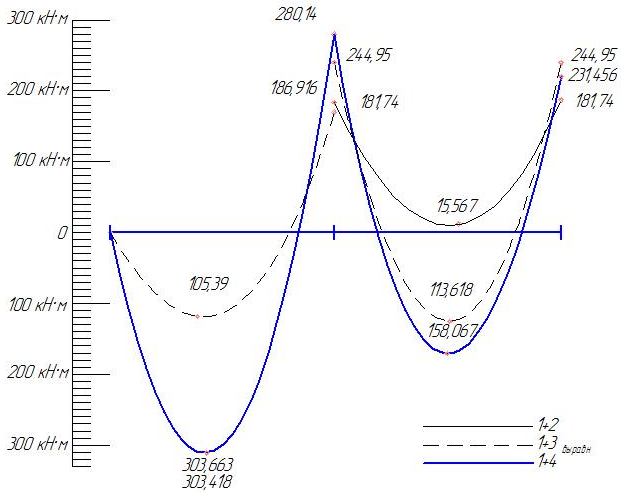Схема загружения	Опорные моменты, кНм				Мmax, кНм		Привязка х, м
	M12	M21	M23	M32	1 пролет	Средний пролет	1 пролет	Средний пролет
1+4	0	280,14	280,14	231,456	303,418	158,067	2,397	2,979

2.2.4. Определение моментов на гранях колонн:

2.2.5. Расчет прочности ригеля по нормальным сечениям.

- Сечение в пролете (пролетная арматура):

<sub>Определяем площадь растянутой арматуры:








Арматура в сжатой зоне по расчету не требуется.</sub>

Принимаем арматуру 425мм, A_ф = 19,63см².

- Сечение на опоре (верхняя стыковая арматура):


<sub>Определяем площадь растянутой арматуры:




Арматура в сжатой зоне по расчету не требуется.</sub>

Принимаем арматуру 322мм, A_ф = 11,4см².

2.2.6. Расчет прочности ригеля по наклонному сечению.

В приопорной зоне (1/4 пролёта) арматура устанавливается с шагом и => s_w=100мм.

В середине пролёта на расстоянии ½ l и s_w=150мм.



Проверим условие по полосе между наклонными трещинами:





350,863<563,569кН

Условие выполняется.
Расчёт плиты на действие поперечной силы по наклонному сечению:



где -поперечная сила в наклонном сечении с длиной проекции С

-поперечная сила воспринимаемая бетоном в наклонном сечении

-поперечная сила воспринимаемая поперечной арматурой в наклонном сечении.

Поперечная арматура класса А300.

Из условия свариваемости устанавливается минимальный диаметр поперечных стержней-8мм, ,

Определим интенсивность хомутов:








Если нагрузка включает временную, то расчётное значение равномерно распределённой нагрузки:



Определяем значение С:





=>



















Условие выполняется.
2.2.7. Построение эпюры материалов.

В целях экономии материала до опоры доводят только 2 стержня пролетной нижней арматуры, а стыковую верхнюю арматуру обрывают, не доводя до середины пролета.

Обрываемые стержни заводятся за точку теоретического обрыва на величину W=20d.

- Найдем точку теоретического обрыва для пролетной арматуры:

Определим изгибающий момент, воспринимаемый расчетным сечением, армированным четырьмя стержнями:

Определим изгибающий момент, воспринимаемый расчетным сечением, армированным двумя стержнями:

Из уравнения моментов определяем расстояние х до сечения теоретического обрыва:

Решая данное квадратное уравнение, получим: х₁=4,135м, х₂=0,651м.





- Найдем точку теоретического обрыва для верхней арматуры:

Определим изгибающий момент, воспринимаемый расчетным сечением, армированным двумя стержнями d=12мм (арматура А300):

Из уравнения моментов определяем расстояние х до сечения теоретического обрыва:

Решая данное квадратное уравнение, получим: х₁=0,127м, х₂=6,52м (значение не принимаем в расчет, т.к. оно больше длины ригеля).