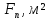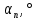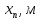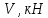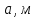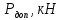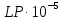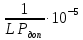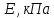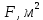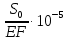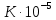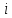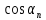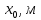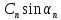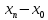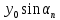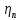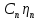Курсовой проект, Набережная с высоким ростверком. Курсовой проект Свайная набережная с высоким ростверком Вариант 18 ст гр. Гт41 Пасынков Д. А
 Скачать 244.58 Kb. Скачать 244.58 Kb.
|
|
Расчет шпунтовых стенок Цель расчета: определить глубину забивки шпунтовой стенки, величину изгибающего момента в ней и подобрать шпунтовые сваи. Шпунтовые стенки набережных с высоким свайным ростверком по схеме своей работы являются заанкерованным больверком. Особенности их расчета вытекают из наличия за шпунтовым рядом вертикальных и наклонных свайных рядов, пересекающих призму обрушения и снижающих активное давление грунта. Положение экранирующей плоскости свайного ряда определяют в соответствии с указаниями. Для набережных с передним шпунтом расчет выполняют с учетом экранирования активного давления сваями. В этом случае призма обрушения грунта позади шпунта пересекается свайным рядом и давление на стенку не может достигнуть своей полной величины, так как часть давления воспринимается сваями. Наличие экранирующей плоскости приводит к тому, что грунт между шпунтовой стенкой и этой плоскостью находится в условиях, аналогичных состоянию сыпучего тела в силосах. Расчёт выполняется в следующей последовательности: 1) Необходимо ограничить призму обрушения, учитывая наличие свободных промежутков между сваями. Для этого определяется положение экранирующей плоскости. В данной работе при принятом шаге свай 1,4 м и диаметре сваи равным 0,32 м построение производится следующим образом (рис. 9): В плане проводятся прямые под углом 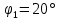 ,касающиеся контура сечения. Образовавшуюся зубчатую заднюю границу грунта заменяют прямой а-а’, делящей пополам расстояние между продольной осью свайного ряда и параллельной ей линией, проходящей через вершины зубцов. ,касающиеся контура сечения. Образовавшуюся зубчатую заднюю границу грунта заменяют прямой а-а’, делящей пополам расстояние между продольной осью свайного ряда и параллельной ей линией, проходящей через вершины зубцов. В результате получаем положение экранирующих плоскостей: Для вертикальной сваи, первой после шпунтовой стенки: Экранирующая плоскость а-а, параллельная свае и расположенная от переднего шпунта на расстоянии 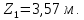 Экранирующая плоскость б-б, параллельная свае и, расположенная на расстоянии 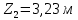 , от экранирующей плоскости второй вертикальной сваи. , от экранирующей плоскости второй вертикальной сваи.Таким образом, ограничиваются две зоны грунта: - I зона – между шпунтовой стенкой и экранирующей плоскостью первого свайного ряда; - II зона – между первой и второй экранирующими плоскостями. 2) Производится построение эпюры давления, действующего на шпунтовую стенку (рис. 10): а) Строится эпюра активного давления грунта I зоны 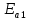 : :Из точки пересечения экранирующей плоскости а1-а1’ с низом ростверка проводится под углом 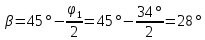 к вертикали линия обрушения аМ. Линия аМ пересекает шпунтовую стенку на глубине hМ =6,7 м. Принимается, что влияние экранирующей плоскости не сказывается до глубины hМ, то есть давления в пределах этой глубины растет по обычному закону к вертикали линия обрушения аМ. Линия аМ пересекает шпунтовую стенку на глубине hМ =6,7 м. Принимается, что влияние экранирующей плоскости не сказывается до глубины hМ, то есть давления в пределах этой глубины растет по обычному закону 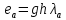 , достигая наибольшего значения на глубине hМ. , достигая наибольшего значения на глубине hМ.Таблица 8 Вычисление абсцисс эпюры активного давления грунта на шпунт
б) Строится эпюра пассивного давления грунта, действующего от отметки дна. Пассивное давление грунта изменяется по глубине по линейному закону: 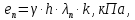 где  - коэффициент пассивного давления грунта; - коэффициент пассивного давления грунта;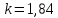 - коэффициент, учитывающий трение грунта о материал шпунтовых свай, определяется в зависимости от угла внутреннего трения: для - коэффициент, учитывающий трение грунта о материал шпунтовых свай, определяется в зависимости от угла внутреннего трения: для 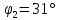 . .Таблица 9 Вычисление абсцисс эпюры пассивного давления грунта
в) Эпюры активного и пассивного давления суммируются и в результате получаем эпюру давления грунта на шпунтовую стенку при рассмотрении I зоны (рис. 8, в). г) Устанавливается влияние грунта, расположенного за первой экранирующей плоскостью. Сопоставляем расстояния  и и 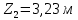 . По рекомендациям при соотношении . По рекомендациям при соотношении  , расчет требуется только с учетом грунта, расположенного в первой зоне. Таким образом, построение эпюры давления, действующего на шпунт, окончено. , расчет требуется только с учетом грунта, расположенного в первой зоне. Таким образом, построение эпюры давления, действующего на шпунт, окончено.д) Полученная эпюра разбивается на отдельные элементы для построения силового многоугольника (рис. 8, д), после чего строится веревочная кривая (см. рис. 8, г). е) Для завершения веревочной кривой проводится замыкающая, уравнивающая три абсциссы: в заделке ростверка, в пролете и в заделке в грунте. Пересечение замыкающей с нижней частью веревочного многоугольника определит точку приложения равнодействующей обратного отпора 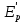 и основную часть глубины забивки и основную часть глубины забивки 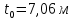 . По условиям решения эта же отметка ограничивает рассчитанную величину пассивных сил . По условиям решения эта же отметка ограничивает рассчитанную величину пассивных сил 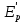 . На эпюре давлений лишние силы отбрасываются, соответствующие изменения внесены и в силовой многоугольник. Окончательная эпюра представлена на рисунке 8. . На эпюре давлений лишние силы отбрасываются, соответствующие изменения внесены и в силовой многоугольник. Окончательная эпюра представлена на рисунке 8.Значения равнодействующей обратного отпора и реакции стенки снимаются с силового многоугольника по средствам параллельного переноса замыкающей в полюсную точку: 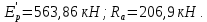 По величине  определяется расстояние от низа стенки до точки приложения: определяется расстояние от низа стенки до точки приложения: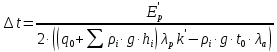 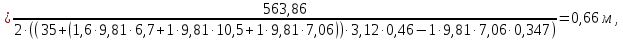 где 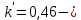 коэффициент, уменьшающий пассивное давление грунта, определяется в зависимости от угла внутреннего трения: для коэффициент, уменьшающий пассивное давление грунта, определяется в зависимости от угла внутреннего трения: для 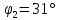 определен интерполяцией. определен интерполяцией.Полная глубина забивки шпунта ниже отметки дна: 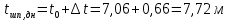 ж) Определяется изгибающий момент от давления грунта, которое воспринимается шпунтовой стенкой:  где 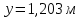 - абсцисса веревочного многоугольника ( - абсцисса веревочного многоугольника (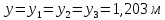 ); ); - полюсное расстояние, измеренное в масштабе сил. - полюсное расстояние, измеренное в масштабе сил.3) Подбор сечения шпунта. Расчетное значение изгибающего момента, по которому следует подбирать шпунтовые сваи из сортамента, равняется максимальному моменту: 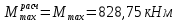 Вычисляем момент сопротивления одного погонного метра стенки, работающей на изгиб по формуле: 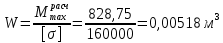 . .По полученному сопротивлению 0,00518 м3 подбираем шпунтовые сваи (таблица 7). Таблица 10 Параметры стальной шпунтовой сваи
6. Статистический расчет свайных набережных 6.1. Основные положения Статический расчет состоит в определении усилий в сваях причальных сооружений. Способ статического расчета набережных с высоким свайным ростверком зависит от жесткости конструкции над основанием. Расчет набережных с жестким ростверком рекомендуется проводить по методу упругого центра. Система в целом представляет собой раму с абсолютно жестким ригелем на упругих опорах-сваях. Основными показателями, характеризующими сваи как опоры ростверка, является несущая способность отдельной сваи и коэффициент ее упругой податливости. Податливость сваи учитывают введением в расчет коэффициента упругой податливости сваи (  ), под которым подразумевают перемещение головы сваи под действием продольной силы ), под которым подразумевают перемещение головы сваи под действием продольной силы 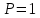 . .Для определения величины коэффициента упругой податливости сваи можно воспользоваться эмпирической формулой Н.А. Смородинского, полученной на основе материалов испытаний свай, проведенных на ряде строительных площадок: 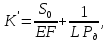 где: 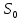 и и 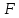 – соответственно свободная длина (м) и поперечное сечение сваи (м2). За свободную длину сваи – соответственно свободная длина (м) и поперечное сечение сваи (м2). За свободную длину сваи 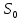 принято считать расстояние от низа ростверка до поверхности естественного грунта; принято считать расстояние от низа ростверка до поверхности естественного грунта;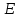 – модуль упругости материала сваи, кПа (для всех видов свай величину условно можно принять – модуль упругости материала сваи, кПа (для всех видов свай величину условно можно принять 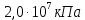 ); );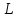 – коэффициент, равный для всех видов свай – коэффициент, равный для всех видов свай 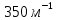 ; ;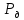 - допускаемая нагрузка на сваю, кН. - допускаемая нагрузка на сваю, кН.Коэффициент упругой податливости при расчетах на один погонный метр длины сооружения следует определять с учетом упругой осадки свай: 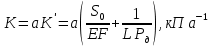 где  – продольный шаг свай, м. – продольный шаг свай, м.При расчете набережных с жестким ростверком методом перемещений удобнее пользоваться коэффициентом упругой осадки свай:  Жесткий ростверк можно считать абсолютно не деформируемым телом на упруго податливых опорах. Это позволяет применить для расчета свайного основания сравнительно простой метод перемещения, когда основную систему получают путем закрепления ростверка связями, предотвращающими любые смещения системы. Расчетную схему набережной принимают с условным шарнирным закреплением свай к ростверку и в основании (включая шпунт, если он несущий). Начало координат принимают на пересечении передней и нижней граней ростверка. Однако, в отличие от общего решения задачи с произвольным выбором точки закрепления, удобнее закрепить рассматриваемую систему в упругом центре. Это позволяет по ходу решения произвести корректировку выбранной схемы с тем, чтобы получить наиболее экономичное решение. Кроме этого, происходит и некоторое упрощение вычислительной работы. При закреплении системы в упругом центре линейными связями: вертикальной - 1, горизонтальной - 2 и угловой - 3 канонические уравнения имеют вид:  где: 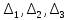 – неизвестные искомые перемещения ростверка по направлению связей 1, 2 и 3; – неизвестные искомые перемещения ростверка по направлению связей 1, 2 и 3;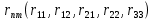 – реакции в связях – реакции в связях  от единичных перемещений по направлению связей от единичных перемещений по направлению связей 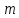 ; ; – реакции в связях от внешней нагрузки. – реакции в связях от внешней нагрузки.Физический смысл канонических уравнений: Ввиду фактического отсутствия связей сумма реакций в каждой из них от перемещений системы и внешней нагрузки равна нулю. Эта система уравнений выражает обычные условия равновесия жесткого тела. По ходу решения задачи необходимо соблюдать правило знаков: перемещения вниз, влево и поворот по часовой стрелке – имеют положительный знак; также будут положительными сжимающие усилия в линейных связях и момент против часовой стрелки. Вычисление реакций в связях от единичных перемещений ростверка производится по формулам: 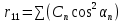 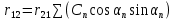 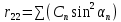 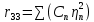 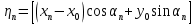 где: 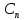 – коэффициент упругой осадки свай; – коэффициент упругой осадки свай;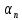 – угол отклонения сваи от вертикали (положительный, если отклоняется по часовой стрелке); – угол отклонения сваи от вертикали (положительный, если отклоняется по часовой стрелке);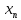 – расстояние от начала координат до головы сваи; – расстояние от начала координат до головы сваи; – координаты упругого центра. – координаты упругого центра. Для определения координат упругого центра служат формулы: 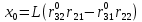  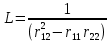 Вспомогательные величины определяются зависимостями:  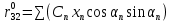 Свободные члены канонических уравнений: 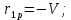  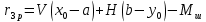 где  и и 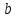 - координаты точки приложения равнодействующей внешних усилий. - координаты точки приложения равнодействующей внешних усилий.После подстановки всех членов в канонические уравнения зависимости для определения перемещений ростверка имеют вид: 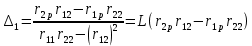 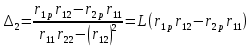 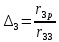 Усилия в сваях определяют по формулам:  где 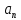 – шаг свай данного ряда. – шаг свай данного ряда.Если расчеты производились с учетом нагрузки на поверхности 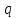 , то в результате получают максимальные усилия в сжатых сваях. Для того, чтобы получить максимальные усилия в растянутых сваях, необходимо повторить расчет по формулам, расположенным выше, подставив в формулу свободных членов канонических уравнений значение , то в результате получают максимальные усилия в сжатых сваях. Для того, чтобы получить максимальные усилия в растянутых сваях, необходимо повторить расчет по формулам, расположенным выше, подставив в формулу свободных членов канонических уравнений значение 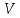 без учета нагрузки без учета нагрузки 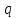 . .В завершении расчета проверяется выполнение условий статики: 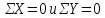 По найденным при статическом расчете усилиям уточняют глубину забивки свай: если полученные усилия превысят несущую способность свай, то следует изменить их длину. 6.2. Статический расчет свайной набережной с жестким ростверком Схема набережной к статическому расчету представлена на рисунке 9. Данные, полученные в результате приближенного расчёта, приведены в таблице 11. Таблица 11 Данные для расчета
Жесткий ростверк рассмотрен как абсолютно не деформируемое тело на упруго податливых опорах. Основная система получена путем закрепления ростверка связями, предотвращающими любые смещения системы. Расчетная схема набережной принята с условным шарнирным закреплением свай к ростверку и в основании, включая шпунт, так как он принят несущим. Начало координат принято на пересечении передней и нижней гранях ростверка. Допускаемую нагрузку на 1 п.м. несущего шпунта, учитывая малую глубину забивки стенки можно определить по упрощенной формуле: 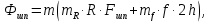 где  – площадь поперечного сечения 1п.м шпунтовой стенки; – площадь поперечного сечения 1п.м шпунтовой стенки; 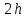 – площадь заглубленного в основании одного погонного метра шпунтовой стенки; – площадь заглубленного в основании одного погонного метра шпунтовой стенки;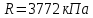 – расчетное сопротивление грунта под нижним концом сваи по таблице СП 24.13330.2011 для суглинков с показателем текучести равном 0,5 (глубина забивки шпунта – расчетное сопротивление грунта под нижним концом сваи по таблице СП 24.13330.2011 для суглинков с показателем текучести равном 0,5 (глубина забивки шпунта 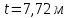 ); );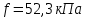 – расчетное сопротивление слоя грунта, соприкасающегося с боковой поверхностью сваи (средняя глубина расположения слоя грунта принята – расчетное сопротивление слоя грунта, соприкасающегося с боковой поверхностью сваи (средняя глубина расположения слоя грунта принята 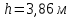 , с учетом того, что её отсчитывают от поверхности грунта основания); , с учетом того, что её отсчитывают от поверхности грунта основания); – коэффициент условий работы грунта под нижним концом шпунта, учитывающий влияние способа погружения шпунта; – коэффициент условий работы грунта под нижним концом шпунта, учитывающий влияние способа погружения шпунта; 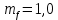 – коэффициент условий работы грунта на боковой поверхности шпунта, учитывающий влияние способа погружения шпунта; – коэффициент условий работы грунта на боковой поверхности шпунта, учитывающий влияние способа погружения шпунта;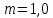 – коэффициент условий работы сваи в грунте. – коэффициент условий работы сваи в грунте. Принимаем данное значение как  для шпунта. для шпунта. Таблица 12 Коэффициенты упругой осадки свай
Таблица 13 Усилия в сваях от единичных смещений
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 25
25