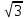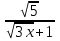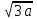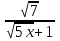тесты 8 класс алгебра. Квадрат тбірлер. Квадрат тбірлерді асиеттері жне оларды есептеулерде олдану. 1 нса А1
 Скачать 151.04 Kb. Скачать 151.04 Kb.
|
|
1 тақырып. Квадрат түбірлер. Квадрат түбірлердің қасиеттері және оларды есептеулерде қолдану. 1 нұсқа А1. Сандарды өсу ретімен орналастыр: 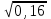 ; 0,4(4); ; 0,4(4); 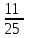 А. 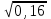 ; 0,4(4); ; 0,4(4); 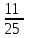 ; Б. 0,4(4); ; Б. 0,4(4); 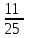 ; ;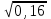 ; В. ; В. 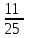 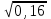 ;0,4(4); Г. ;0,4(4); Г. 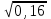 ; ;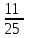 ;0,4(4); ;0,4(4);А2. 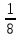 саны мына санның арифметикалық түбірі: саны мына санның арифметикалық түбірі:А. 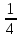 Б. 0,64 В. Б. 0,64 В. 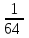 Г. Г. 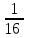 А3. Есепте 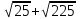 А. 30 Б. 20 В. 25 Г. 35 А4. Өрнекті ықшамда: 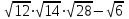 А. 13 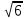 Б. 27 Б. 27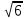 В. 14 В. 14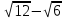 Г. 55 Г. 55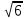 А5. Есепте: 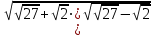 А. 5 Б. 25 В. 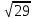 Г. Г. 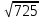 В1. Амалды орында: 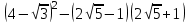 . .Жауабы: __________________________ В2. Бөлшекті қысқарт: 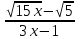 . .Жауабы: __________________________ В3. Өрнекті ықшамда 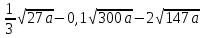 . .Жауабы: __________________________ С1. Бөлшекті қысқарт: 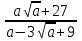 . .С2. Өрнектің мәнін тап 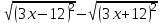 мұнд. х=-2007. мұнд. х=-2007.2 нұсқа А1. Сандарды өсу ретімен орналастыр 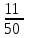 ; 0,2(2); ; 0,2(2); 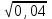 А. 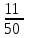 ; 0,2(2); ; 0,2(2); 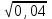 Б. Б.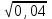 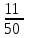 ; 0,2(2); В. 0,2(2); ; 0,2(2); В. 0,2(2);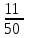 ; ;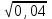 Г. Г.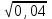 ;0,2(2); ;0,2(2);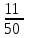 ; ; А2. 0,8 саны мына санның арифметикалық квадрат түбірі болады: А. 1,6 Б. 0,64 В. 0,064 Г. 6,4 А3. Есепте 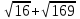 А. 17 Б. 25 В. 23 Г. 27 А4. Өрнекті ықшамда 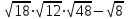 А. 7 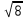 Б. 24 Б. 24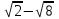 В. 70 В. 70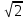 Г. 35 Г. 35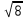 А5. Есепте: 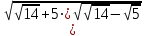 А. 3 Б. 9 В. 19 Г. 70 В1. Амалды орында: 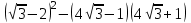 . .Жауабы: __________________________ В2. Бөлшекті қысқарт 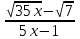 . .Жауабы: __________________________ В3. Өрнекті ықшамда 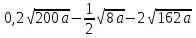 . .Жауабы: __________________________ С1. Бөлшекті қысқарт: 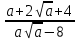 . .С2. Өрнектің мәнін тап 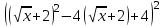 мұнд. х=27. мұнд. х=27.
Жауабы Шешуі С1 и С2: 1нұсқа С1. 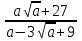 = =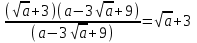 . .жауабы: 3+ 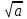 С2. 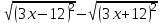 =|3х-12|-|3х+12|=-3х+12+3х+12=24, егер -2007 =|3х-12|-|3х+12|=-3х+12+3х+12=24, егер -2007жауабы: 24 2нұсқа С1. 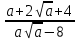 = =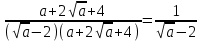 . .жауабы: С2. 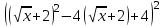 =(( =((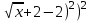 =х2, 272=729 =х2, 272=729Ответ: 729. 2 тақырып. Квадрат теңдеулер:квадрат теңдеудің формуласы. Рационал теңдеулерді шешу. 1нұсқа А1. Квадрат теңдеу: А. 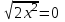 Б. 3х-9х2=0 В. 42х-22=0 Г. 5х2-х3+2=0 Б. 3х-9х2=0 В. 42х-22=0 Г. 5х2-х3+2=0А2. Теңдеудің түбірлерін тап -2х2+32=0 А. түбірі жоқ Б. 16 В. ±4 Г. ±8 А3. Теңдеуді шеш -5х2+ 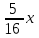 =0. Жауабында ең кіші түбірін көрсет =0. Жауабында ең кіші түбірін көрсетА. 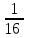 Б. 0 В. - Б. 0 В. -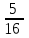 Г. - Г. -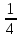 А4. Теңдеудің дискриминантын есепте:7х2-5х-3=0 А. -3 Б. 53 В. 109 Г. -59 А5. Теріс таңбалы түбірін тап 3х2-2х-1=0. А. - 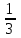 Б. -1 В. - Б. -1 В. -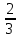 Г. -2 Г. -2В1.Теңдеудің түбірлер санын көрсет: 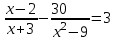 . .Жауабы: __________________________ В2. Теңдеудің х2+рx-28=0 түбірлерінің бірі 7-ге тең. Түбірлерінің қосындысын тап Жауабы: __________________________ В3. Теңдеуді шеш х4-11х2-12=0. Жауабы: __________________________ С1. а-ның ең кіші мәнін көрсет, 3х2-2ах+12=0 теңдеуінің тек бір ғана шешімі болатындай. С2. Теңдеуді шеш 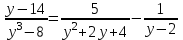 2нұсқа А1. Квадрат теңдеу А.15х-5х2=0 Б. 2х2-3х3+5=0 В. 42 - х=0 Г. 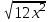 =0 =0А2. Теңдеудің түбірлері 9х-х2=0 А. нақты түбірлері жоқ Б. 0; -9 В. 0; 9 Г. 9 А3. Теңдеуді шеш: -4х2+ 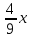 =0. Жауабында түбірлерінің ең үлкенін көрсет: =0. Жауабында түбірлерінің ең үлкенін көрсет:А.0 Б. 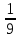 В. - В. -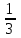 Г. - Г. -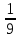 А4. Теңдеудің дискриминантын тап: 10х2-3х+4=0 А. 169 Б. -39 В. 163 Г. -151 А5. Теңдеудің теріс таңбалы түбірін тап: 4х2+4х-3=0. А. – 1,5 Б. -0,5 В. -1,25 Г. -3 В1. Теңдеудің түбірлер санын көрсет: 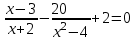 . .Жауабы: __________________________ В2. Теңдеудің х2+рx-32=0 бір түбірі 8-ге тең. Теңдеудің түбірлерінің қосындысын тап Жауабы: __________________________ В3.Теңдеуді шеш х4-17х2-18=0. Жауабы: __________________________ С1. а-ның ең кіші мәнін көрсет, мұндағы7х2+ах+7=0 теңдеуінің тек бір ғана шешімі болатындай С2. Теңдеуді шеш 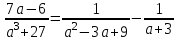 . .
Шешуі: С1 и С2: 1нұсқа С1. 3х2-2ах+12=0, D=(-2а)2-4∙3∙12=4а2-144, 4а2-144=0, 4а2=144, а2=36, а=±6, а=-6-ең кіші мәні Жауабы: -6 С2. 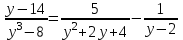 , ,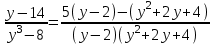 , у≠2 , у≠2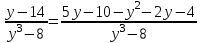 , , y-14=-y2+3y-14, у2-2у=0 у(у-2)=0 у=0және у=2-түбірі бола алмайды жауабы: 0 2 нұсқа С1. 7х2+ах+7=0, D=а2-196, а2-196=0, а2=196, а=±14, -14- ең кіші мәні Жауабы: -14 С2. 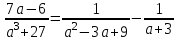 , ,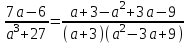 , ,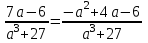 , а≠-3 , а≠-37а-6=-а2+4а-6, а2+3а=0, а(а+3)=0 а=0 немесе а=-3-түбірі бола алмайды Жауабы: 0 3 тақырып. Квадрат үшмүше. Виет теоремасы. Квадрат үшмүшені көбейткіштерге жіктеу. 1 нұсқа А1. Квадрат үшмүшені көбейткіштерге жікте х2-6х+8. А. (4-х)(2-х) Б. (х-4)(х-2) В. (х+2)(х+4) Г. (х-2)(х+4) А2. Бөлшекті қысқарт: 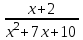 . .А. х+5 Б. 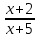 В. В. 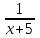 Г. Г. 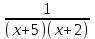 А3. Көбейткіштерге жікте: 7х2-8х+1. А. (х-1) 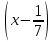 Б. (х+1) Б. (х+1)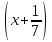 В. 7(х+1) В. 7(х+1)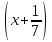 Г. 7(х-1) Г. 7(х-1)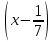 . . А4. Түбірлері 2 және 5болатын квадрат теңдеуді жаз:. А. х2+10х-7=0 Б. х2-7х-10=0 В. х2+7х+10=0 Г. х2-7х+10=0 А5. Теңдеудің түбірлерінің қосындысы мен көбейтіндісін тап: х2-12х-45=0 А. 12; -45 Б. 12; 45 В. -12; -45 Г. -12; 45 В1. Квадрат теңдеудің бір түбірі -3-ке тең. Коэффициенті k мен екінші түбірін тап: х2+kх+18=0. Жауабы: __________________________ В2. Сәйкестеу арқылы түбірлерін тап: х2-17х+42=0. Жауабы: __________________________ В3. Теңдеуді шешпей,түбірлерінің(бар болса) таңбасын анықта: 3у2-23у+21=0. Жауабы: __________________________ С1. Бөлшекті қысқарт: 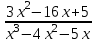 . .С2. х1 және х2 – теңдеудің түбірлері х2+7х-11=0. Теңдеуді шешпей мағынасын тап: 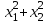 . . 2нұсқа А1. Квадрат үшмүшені көбейткіштерге жікте х2+4х-12. А. (х-2)(х+6) Б. (х-2)(х-6) В. (х+2)(х-6) Г. (х+2)(х+6) А2. Бөлшекті қысқарт: 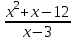 . .А. х-4 Б. 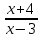 В. х+4 Г. В. х+4 Г. 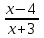 А3. Жікте:12х2-7х+1. А. 12(х- 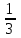 )(х- )(х-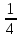 ) Б. (х- ) Б. (х-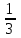 )(х- )(х-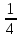 ) В. (х+ ) В. (х+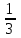 )(х+ )(х+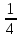 ) Г. 12(х+ ) Г. 12(х+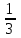 )(х+ )(х+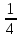 ) ) А4. Түбірлері -1 және 3болатын теңдеуді жаз. А. х2+2х-3=0 Б. х2-2х+3=0 В. х2+2х+3=0 Г. х2-2х-3=0 А5.Теңдеудің түбірлерінің қосындысы мен көбейтіндісін тап: х2+12х-45=0 А. -12; -45 Б. 12; 45 В. 12; -45 Г. -12; 45 В1. Теңдеудің түбірлерінің бірі -2-ге тең. Коэффициенті k мен екінші түбірін тап:х2+kх-16=0. Жауабы: __________________________ В2. Сәйкестендіру арқылы теңдеудің түбірін тап:: х2-2х-15=0. Жауабы: __________________________ В3. Теңдеудің түбірлерінің (бар болса)таңбасын анықта: 3у2-21у+17=0. Жауабы: __________________________ С1. Бөлшекті қысқарт: 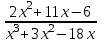 . .С2. х1 жәнех2 теңдеудің түбірлері х2-9х-17=0. Теңдеуді шешпей мағынасын анықта: 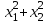 . .
Шешуі: С1 и С2: 1нұсқа С1. 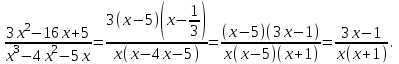 3х2-16х+5, D=196, х1=5, х2= 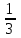 . х2-4х-5, D=36, х1=5, х2=-1. . х2-4х-5, D=36, х1=5, х2=-1.Жауабы: С2. х2+7х-11=0 х1+х2=-7 х1х2=-11 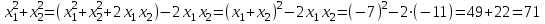 . .Жауабы: 71 2нұсқа С1. 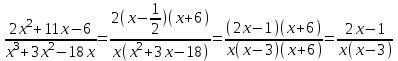 . .2х2+11х-6, D=169, х1= 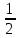 , х2=-6 х2+3х-18, D=81, х1=3, х2=-6. , х2=-6 х2+3х-18, D=81, х1=3, х2=-6.Жауабы: 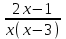 . .С2. х2-9х-17=0 х1+х2=9 х1х2=-17 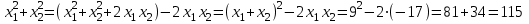 Жауабы: 115. Жауабы: 115. |