Квадратты интегралды мартингал болсын делік. Онда (2) формула
 Скачать 16.17 Kb.
|
|
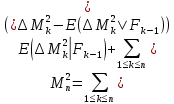2)  квадратты интегралды мартингал болсын делік  , .Онда (2) формула  -ге қолданылған мына түрге ие болады: Бұл жердегі 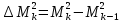 .Сонда: 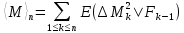  Бұл белгімен (6)-шы кеңейтуді мына формада жазуға болады: 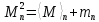 Мұндағы 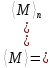 (болжамды) реттілік М мартингалының квадраттық сипаттамасы деп аталады.  ескере отырып, келесідегідей болады: 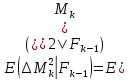 Бұл қасиет  квадраттық сипаттамасын М квадраттық (квадрат интегралды) болжамды квадраттық вариация деп те атайтынын түсіндіреді.Бұл ретте квадраттық вариация термині үшін жазылған: 3) Енді 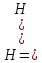 реттілігінің өзі мартингал болып табылады және оның үстіне квадрат интегралды,яғни: 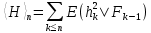 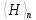 квадраттық характеристикасын тұратын  шамасы H мартингалінің өзгергіштігінің (құбылмалылығының) дәрежесін және көп жағдайда оның қасиеттерін анықтайды. Мысалы, егер  бірлікті ықтималдық бар болса,онда H квадрат интегралды мартингал үшін бар үлкен сандардың күшейтілген заңы  үшін мынаған тең болады:  Егер шартты матеиматикалық күтім 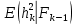 шартсыз  -мен сәйкес болса, онда тұрақсыздық - бұл тек  дисперсияларының жиынтығы. |