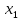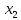ММДО_лаб1. ММДО_лаб1_ІПЗк-20-1_Миколюк. Лабораторна робота 1 Тема Графічний метод розвязання задач лінійного програмування (ЛП)
 Скачать 1.15 Mb. Скачать 1.15 Mb.
|
 Лабораторна робота № 1 Тема: Графічний метод розв’язання задач лінійного програмування (ЛП) 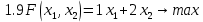 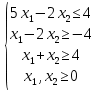 Спочатку побудуємо на площині, у декартовій прямокутній системі координат, область допустимих розв’язків (ОДР) задачі, що визначається системою умов-обмежень. Кожна із нерівностей задає на площині відповідну напівплощину. Для того, щоб її визначити, потрібно побудувати відповідну пряму, яка розділяє площину на дві напівплощини та визначити, в якій з них виконуватиметься нерівність. Визначена напівплощина позначається відповідним штрихуванням. У нашій задачі матимемо: 1-ша пряма 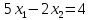
2-га пряма 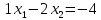
3-тя пряма 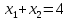
Побудуємо область допустимих рішень(розв'яжемо графічно систему нерівностей). Для цього побудуємо кожну пряму та визначимо півплощини, задані нерівностями (напівплощини позначені штрихом). 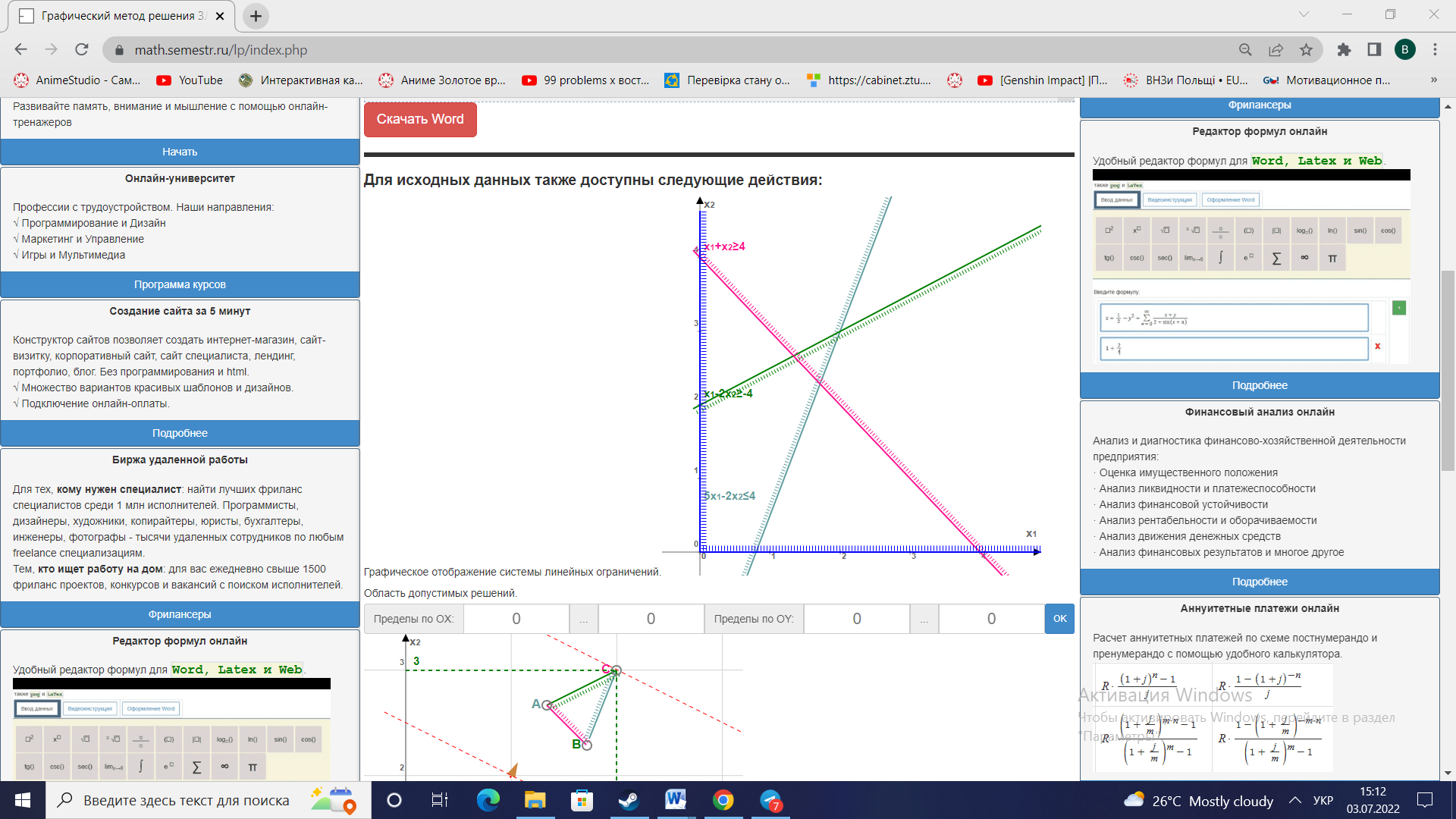 ОДР являтиме собою область перетину п’яти знайдених областей – трикутник АBC.  Будуємо вектор, координатами якого є коефіцієнти функції F. Початок в точці (0;0).  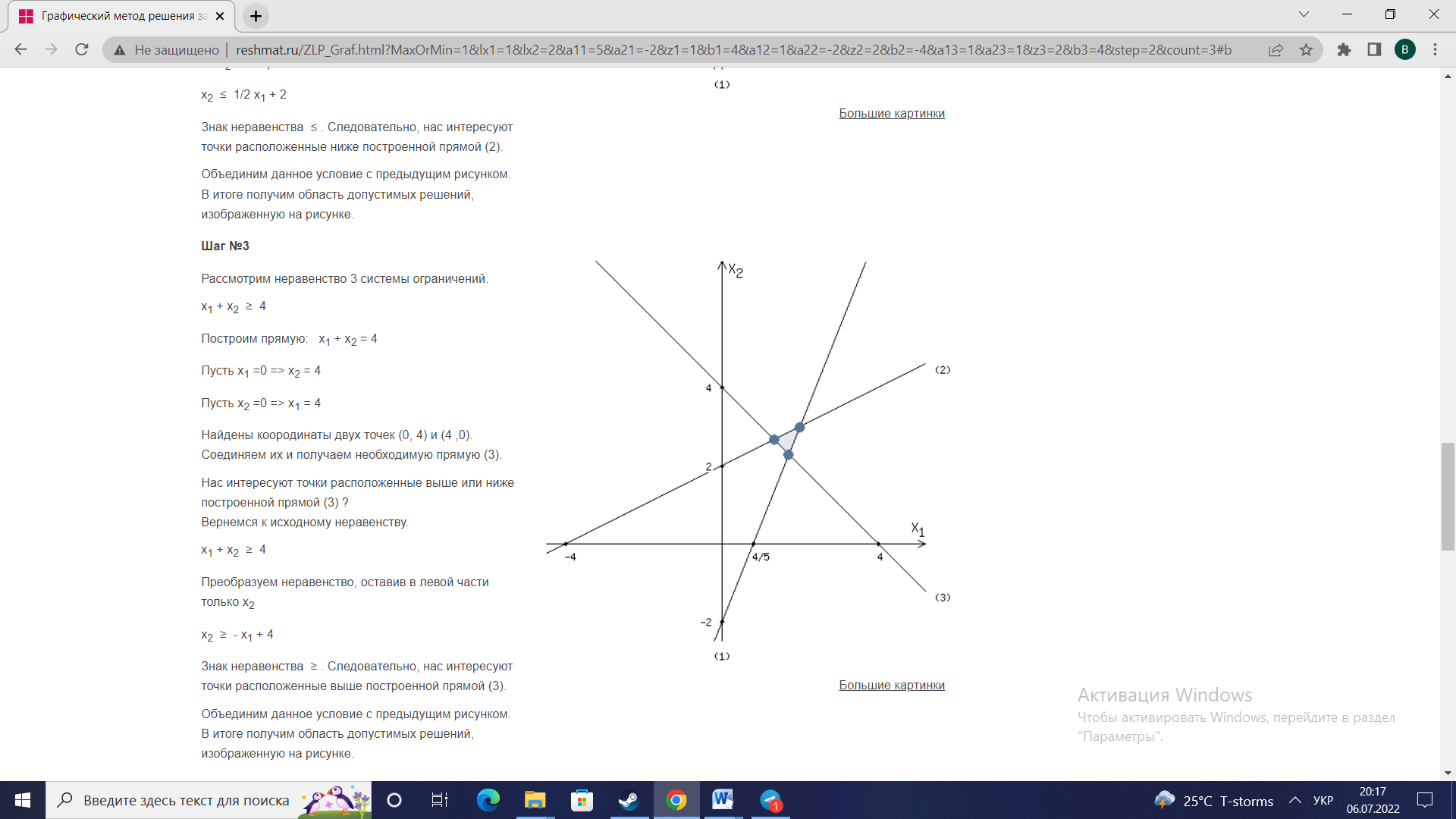 Переміщуємо червону пряму, перпендикулярно вектору C, від лівого нижнього кутка до правого верхнього. 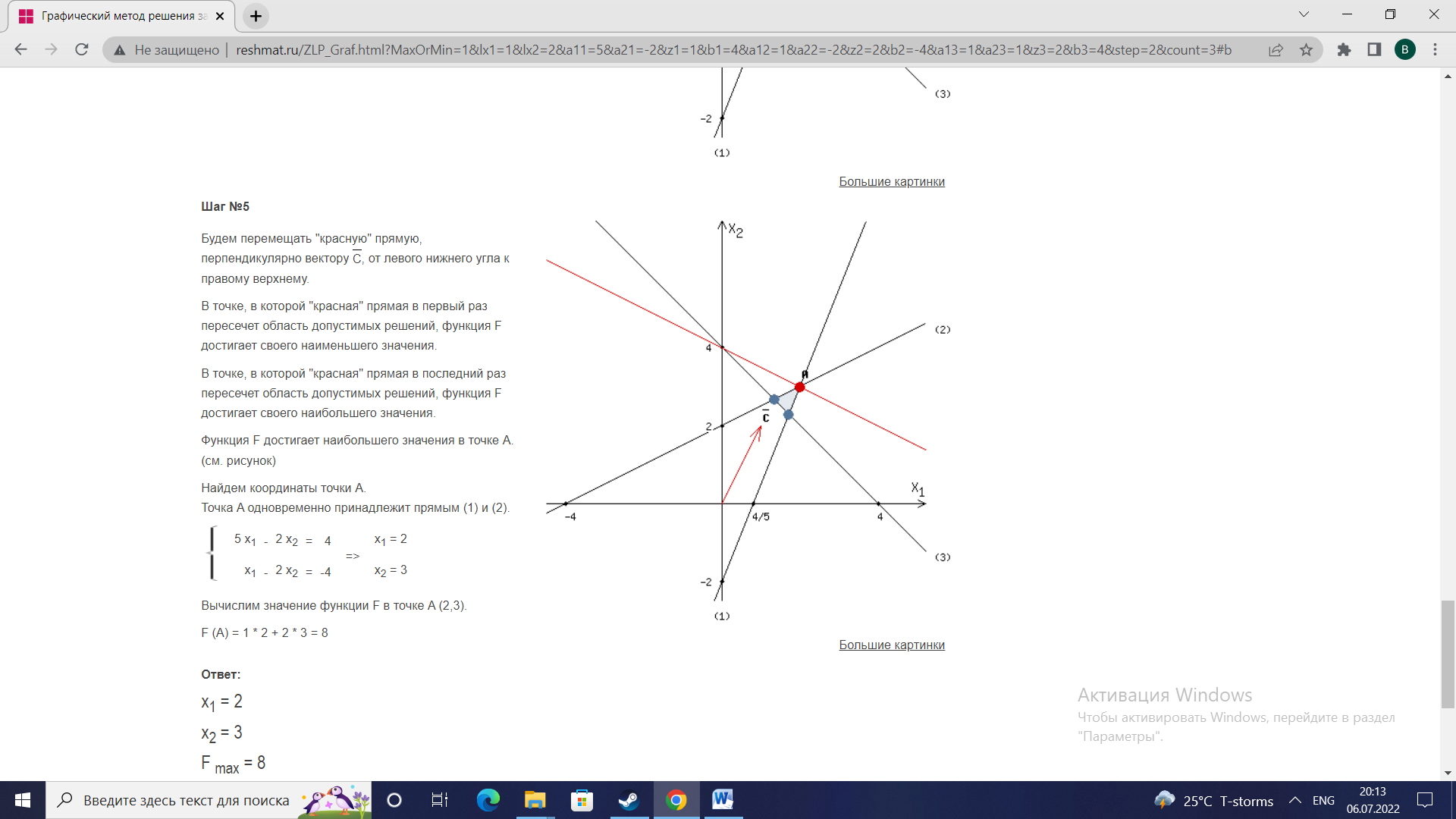 В точці, в якій червона пряма вперше перетне область допустимих значень, функція F досягає свого найменшого значення. В точці, в якій червона пряма в останнє перетне область допустимих значень, функція F досягає свого найбільшого значення. Функція F досягає свого найбільшого значення в точці А. Знайдемо координати точки А. Точка А одночасно належить прямим (1) и та (2). 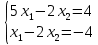 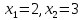 Обчислимо значення функції F в точці А(2;3) F(A) = 1*2 + 2*3 =8 Відповідь: 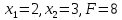 |